Including Leaf Traits Improves a Deep Neural Network Model for Predicting Photosynthetic Capacity from Reflectance
Abstract
:1. Introduction
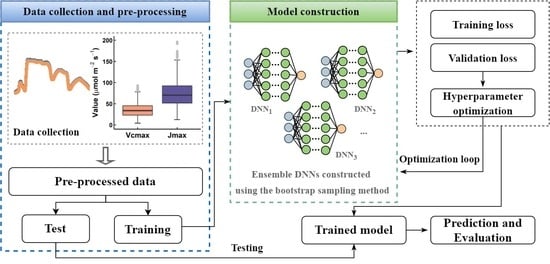
2. Materials and Methods
2.1. The Naeba Dataset
2.2. DNN Model Construction
2.3. Other Leaf Biophysical/Biochemical Traits as Additional Predictors
2.4. Performance Evaluation
3. Results
3.1. Performance of DNN Models for Predicting Vcmax and Jmax from Reflectance
3.2. Performance of DNN Models for Predicting Vcmax and Jmax from Reflectance in Different Leaf Types
3.3. Performance of DNN Models for Predicting Vcmax and Jmax from Reflectance during Different Growing Periods
3.4. Leaf Biophysical/Biochemical Traits as Additional Predictors of DNN Models
4. Discussion
4.1. Estimation of Leaf Photosynthetic Traits from Spectra Using the DNN Models
4.2. Including Other Leaf Biophysical/Biochemical Traits to Better Predict Photosynthetic Capacity from Reflectance Using DNN Models
4.3. Bootstrap as a Remedy for Setting Up Robust DNN Models from Limited Samples
4.4. Limits and Future Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bernacchi, C.J.; Bagley, J.E.; Serbin, S.P.; Ruiz-Vera, U.M.; Rosenthal, D.M.; Vanloocke, A. Modelling C3 photosynthesis from the chloroplast to the ecosystem. Plant Cell Environ. 2013, 36, 1641–1657. [Google Scholar] [CrossRef] [PubMed]
- Farquhar, G.D.; von Caemmerer, S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rogers, A.; Medlyn, B.E.; Dukes, J.S.; Bonan, G.; von Caemmerer, S.; Dietze, M.C.; Kattge, J.; Leakey, A.D.B.; Mercado, L.M.; Niinemets, Ü.; et al. A roadmap for improving the representation of photosynthesis in Earth system models. New Phytol. 2017, 213, 22–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Long, S.P.; Bernacchi, C.J. Gas exchange measurements, what can they tell us about the underlying limitations to photosynthesis? Procedures and sources of error. J. Exp. Bot. 2003, 54, 2393–2401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Albert, L.P.; Wu, J.; Prohaska, N.; de Camargo, P.B.; Huxman, T.E.; Tribuzy, E.S.; Ivanov, V.Y.; Oliveira, R.S.; Garcia, S.; Smith, M.N.; et al. Age-dependent leaf physiology and consequences for crown-scale carbon uptake during the dry season in an Amazon evergreen forest. New Phytol. 2018, 219, 870–884. [Google Scholar] [CrossRef] [Green Version]
- Burnett, A.C.; Serbin, S.P.; Lamour, J.; Anderson, J.; Davidson, K.J.; Yang, D.; Rogers, A. Seasonal trends in photosynthesis and leaf traits in scarlet oak. Tree Physiol. 2021, 41, 1413–1424. [Google Scholar] [CrossRef] [PubMed]
- Song, G.; Wang, Q.; Jin, J. Exploring the instability of the relationship between maximum potential electron transport rate and maximum carboxylation rate in cool-temperate deciduous forests. Agric. For. Meteorol. 2021, 308–309, 108614. [Google Scholar] [CrossRef]
- van de Weg, M.J.; Meir, P.; Grace, J.; Ramos, G.D. Photosynthetic parameters, dark respiration and leaf traits in the canopy of a Peruvian tropical montane cloud forest. Oecologia 2012, 168, 23–34. [Google Scholar] [CrossRef] [PubMed]
- Dechant, B.; Cuntz, M.; Vohland, M.; Schulz, E.; Doktor, D. Estimation of photosynthesis traits from leaf reflectance spectra: Correlation to nitrogen content as the dominant mechanism. Remote Sens. Environ. 2017, 196, 279–292. [Google Scholar] [CrossRef]
- Silva-Perez, V.; Molero, G.; Serbin, S.P.; Condon, A.G.; Reynolds, M.P.; Furbank, R.T.; Evans, J.R. Hyperspectral reflectance as a tool to measure biochemical and physiological traits in wheat. J. Exp. Bot. 2018, 69, 483–496. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Rogers, A.; Albert, L.P.; Ely, K.; Prohaska, N.; Wolfe, B.T.; Oliveira, R.C.; Saleska, S.R.; Serbin, S.P. Leaf reflectance spectroscopy captures variation in carboxylation capacity across species, canopy environment and leaf age in lowland moist tropical forests. New Phytol. 2019, 224, 663–674. [Google Scholar] [CrossRef] [PubMed]
- Fu, P.; Meacham-Hensold, K.; Guan, K.; Wu, J.; Bernacchi, C. Estimating photosynthetic traits from reflectance spectra: A synthesis of spectral indices, numerical inversion, and partial least square regression. Plant Cell Environ. 2020, 1241–1258. [Google Scholar] [CrossRef] [PubMed]
- Heckmann, D.; Schlüter, U.; Weber, A.P.M. Machine learning techniques for predicting crop photosynthetic capacity from leaf reflectance spectra. Mol. Plant 2017, 10, 878–890. [Google Scholar] [CrossRef] [Green Version]
- Serbin, S.P.; Dillaway, D.N.; Kruger, E.L.; Townsend, P.A. Leaf optical properties reflect variation in photosynthetic metabolism and its sensitivity to temperature. J. Exp. Bot. 2012, 63, 489–502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ali, A.A.; Xu, C.; Rogers, A.; McDowell, N.G.; Medlyn, B.E.; Fisher, R.A.; Wullschleger, S.D.; Reich, P.B.; Vrugt, J.A.; Bauerle, W.L.; et al. Global-scale environmental control of plant photosynthetic capacity. Ecol. Appl. 2015, 25, 2349–2365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, N.G.; Keenan, T.F.; Colin Prentice, I.; Wang, H.; Wright, I.J.; Niinemets, Ü.; Crous, K.Y.; Domingues, T.F.; Guerrieri, R.; Yoko Ishida, F.; et al. Global photosynthetic capacity is optimized to the environment. Ecol. Lett. 2019, 22, 506–517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ainsworth, E.A.; Serbin, S.P.; Skoneczka, J.A.; Townsend, P.A. Using leaf optical properties to detect ozone effects on foliar biochemistry. Photosynth. Res. 2014, 119, 65–76. [Google Scholar] [CrossRef] [PubMed]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Houborg, R.; Anderson, M.C.; Daughtry, C.S.T.; Kustas, W.P.; Rodell, M. Using leaf chlorophyll to parameterize light-use-efficiency within a thermal-based carbon, water and energy exchange model. Remote Sens. Environ. 2011, 115, 1694–1705. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Phil. Trans. R Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Iio, A.; Kakubari, Y. Broadband simple ratio closely traced seasonal trajectory of canopy photosynthetic capacity. Geophys. Res. Lett. 2008, 35, L07401. [Google Scholar] [CrossRef]
- DuBois, S.; Desai, A.R.; Singh, A.; Serbin, S.P.; Goulden, M.L.; Baldocchi, D.D.; Ma, S.; Oechel, W.C.; Wharton, S.; Kruger, E.L.; et al. Using imaging spectroscopy to detect variation in terrestrial ecosystem productivity across a water-stressed landscape. Ecol. Appl. 2018, 28, 1313–1324. [Google Scholar] [CrossRef]
- Muraoka, H.; Noda, H.M.; Nagai, S.; Motohka, T.; Saitoh, T.M.; Nasahara, K.N.; Saigusa, N. Spectral vegetation indices as the indicator of canopy photosynthetic productivity in a deciduous broadleaf forest. J. Plant Ecol. 2013, 6, 393–407. [Google Scholar] [CrossRef] [Green Version]
- Yendrek, C.R.; Tomaz, T.; Montes, C.M.; Cao, Y.; Morse, A.M.; Brown, P.J.; McIntyre, L.M.; Leakey, A.D.B.; Ainsworth, E.A. High-throughput phenotyping of maize leaf physiological and biochemical traits using hyperspectral reflectance. Plant Physiol. 2017, 173, 614–626. [Google Scholar] [CrossRef] [PubMed]
- Song, G.; Wang, Q.; Jin, J. Temporal instability of partial least squares regressions for estimating leaf photosynthetic traits from hyperspectral information. 2021; under review. [Google Scholar]
- Fu, P.; Meacham-Hensold, K.; Guan, K.; Bernacchi, C.J. Hyperspectral leaf reflectance as proxy for photosynthetic capacities: An ensemble approach based on multiple machine learning algorithms. Front. Plant Sci. 2019, 10, 1–13. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Kamarudin, M.H.; Ismail, Z.H.; Saidi, N.B. Deep learning sensor fusion in plant water stress assessment: A comprehensive review. Appl. Sci. 2021, 11, 1403. [Google Scholar] [CrossRef]
- Cai, Y.; Zheng, W.; Zhang, X.; Zhangzhong, L.; Xue, X. Research on soil moisture prediction model based on deep learning. PLoS ONE 2019, 14, e0214508. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, L.B.; da Cunha, F.F. New approach to estimate daily reference evapotranspiration based on hourly temperature and relative humidity using machine learning and deep learning. Agric. Water Manag. 2020, 234, 106113. [Google Scholar] [CrossRef]
- Fariñas, M.D.; Jimenez-Carretero, D.; Sancho-Knapik, D.; Peguero-Pina, J.J.; Gil-Pelegrín, E.; Gómez Álvarez-Arenas, T. Instantaneous and non-destructive relative water content estimation from deep learning applied to resonant ultrasonic spectra of plant leaves. Plant Methods 2019, 15, 1–10. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modeling of the Punjab Northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Dalto, M.; Matusko, J.; Vasak, M. Deep neural networks for ultra-short-term wind forecasting. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 1657–1663. [Google Scholar]
- Ryu, S.; Noh, J.; Kim, H. Deep neural network based demand side short term load forecasting. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications (SmartGridComm), Sydney, Australia, 6–9 November 2016; pp. 308–313. [Google Scholar]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.; Navdeep, J. Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Zhao, Z.Q.; Zheng, P.; Xu, S.T.; Wu, X. Object detection with deep learning: A review. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3212–3232. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, X.; Huang, Y.; Shang, G.; Zhou, C.; Cheng, T.; Tian, Y.; Cao, W.; Zhu, Y. Evaluation of six algorithms to monitor wheat leaf nitrogen concentration. Remote Sens. 2015, 7, 14939–14966. [Google Scholar] [CrossRef] [Green Version]
- Alhnaity, B.; Pearson, S.; Leontidis, G.; Kollias, S. Using deep learning to predict plant growth and yield in greenhouse environments. Acta Hortic. 2020, 1296, 425–431. [Google Scholar] [CrossRef]
- Kaul, M.; Hill, R.L.; Walthall, C. Artificial neural networks for corn and soybean yield prediction. Agric. Syst. 2005, 85, 1–18. [Google Scholar] [CrossRef]
- Kim, N.; Lee, Y.W. Machine learning approaches to corn yield estimation using satellite images and climate data: A case of Iowa State. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2016, 34, 383–390. [Google Scholar] [CrossRef] [Green Version]
- Kuwata, K.; Shibasaki, R. Estimating crop yields with deep learning and remotely sensed data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 858–861. [Google Scholar]
- Shahhosseini, M.; Hu, G.; Khaki, S.; Archontoulis, S.V. Corn yield prediction with ensemble CNN-DNN. Front. Plant Sci. 2021, 12, 1–13. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Choi, C.; Shin, D.H.; Kim, H.S. Prediction of heavy rain damage using deep learning. Water 2020, 12, 1942. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Rew, J.; Cho, Y.; Hwang, E. A robust prediction model for species distribution using bagging ensembles with deep neural networks. Remote Sens. 2021, 13, 1495. [Google Scholar] [CrossRef]
- Mi, X.; Zou, F.; Zhu, R. Bagging and deep learning in optimal individualized treatment rules. Biometrics 2019, 75, 674–684. [Google Scholar] [CrossRef] [PubMed]
- Mi, X.; Zou, B.; Zou, F.; Hu, J. Permutation-based identification of important biomarkers for complex diseases via machine learning models. Nat. Commun. 2021, 12, 1–12. [Google Scholar] [CrossRef]
- Emadi, M.; Taghizadeh-Mehrjardi, R.; Cherati, A.; Danesh, M.; Mosavi, A.; Scholten, T. Predicting and mapping of soil organic carbon using machine learning algorithms in Northern Iran. Remote Sens. 2020, 12, 2234. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Deep neural network algorithm for estimating maize biomass based on simulated Sentinel 2A vegetation indices and leaf area index. Crop J. 2020, 8, 87–97. [Google Scholar] [CrossRef]
- Merkel, G.D.; Povinelli, R.J.; Brown, R.H. Short-term load forecasting of natural gas with deep neural network regression. Energies 2018, 11, 2008. [Google Scholar] [CrossRef] [Green Version]
- Schmidhuber, J. Deep Learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Dargan, S.; Kumar, M.; Ayyagari, M.R.; Kumar, G. A survey of deep learning and its applications: A new paradigm to machine learning. Arch. Comput. Methods Eng. 2020, 27, 1071–1092. [Google Scholar] [CrossRef]
- Tiwari, S. A comparative study of deep learning models with handcraft features and non-handcraft features for automatic plant species identification. Int. J. Agric. Environ. Inf. Syst. 2020, 11, 44–57. [Google Scholar] [CrossRef]
- Tripathi, S.; Acharya, S.; Sharma, R.D.; Mittal, S.; Bhattacharya, S. Using deep and convolutional neural networks for accurate emotion classification on deap dataset. In Proceedings of the Twenty-Ninth AAAI Conference on Innovative Applications (IAAI-17), Hawaiian, HI, USA, 6–9 February 2017; pp. 4746–4752. [Google Scholar]
- Elbeltagi, A.; Deng, J.; Wang, K.; Malik, A.; Maroufpoor, S. Modeling long-term dynamics of crop evapotranspiration using deep learning in a semi-arid environment. Agric. Water Manag. 2020, 241, 106334. [Google Scholar] [CrossRef]
- Wang, Q.; IIo, A.; Tenhunen, J.; Kakubari, Y. Annual and seasonal variations in photosynthetic capacity of Fagus crenata along an elevation gradient in the Naeba Mountains, Japan. Tree Physiol. 2008, 28, 277–285. [Google Scholar] [CrossRef] [Green Version]
- Foley, S.; Rivard, B.; Sanchez-Azofeifa, G.A.; Calvo, J. Foliar spectral properties following leaf clipping and implications for handling techniques. Remote Sens. Environ. 2006, 103, 265–275. [Google Scholar] [CrossRef]
- Duursma, R.A. Plantecophys—An R package for analysing and modelling leaf gas exchange data. PLoS ONE 2015, 10, e0143346. [Google Scholar] [CrossRef] [PubMed]
- Sonobe, R.; Wang, Q. Towards a universal hyperspectral index to assess chlorophyll content in deciduous forests. Remote Sens. 2017, 9, 191. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar] [CrossRef] [Green Version]
- Chernick, M.R. Bootstrap Methods: A Guide for Practitioners and Researchers, 2nd ed.; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Chang, C.W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-infrared reflectance spectroscopy-principal components regression analyses of soil properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef] [Green Version]
- Meacham-Hensold, K.; Fu, P.; Wu, J.; Serbin, S.; Montes, C.M.; Ainsworth, E.; Guan, K.; Dracup, E.; Pederson, T.; Driever, S.; et al. Plot-level rapid screening for photosynthetic parameters using proximal hyperspectral imaging. J. Exp. Bot. 2020, 71, 2312–2328. [Google Scholar] [CrossRef]
- Wang, S.; Guan, K.; Wang, Z.; Ainsworth, E.A.; Zheng, T.; Townsend, P.A.; Li, K.; Moller, C.; Wu, G.; Jiang, C. Unique contributions of chlorophyll and nitrogen to predict crop photosynthetic capacity from leaf spectroscopy. J. Exp. Bot. 2020, 72, 341–354. [Google Scholar] [CrossRef]
- Kawamura, K.; Nishigaki, T.; Andriamananjara, A.; Rakotonindrina, H.; Tsujimoto, Y.; Moritsuka, N.; Rabenarivo, M.; Razafimbelo, T. Using a one-dimensional convolutional neural network on visible and near-infrared spectroscopy to improve soil phosphorus prediction in Madagascar. Remote Sens. 2021, 13, 1519. [Google Scholar] [CrossRef]
- Ng, W.; Minasny, B.; Montazerolghaem, M.; Padarian, J.; Ferguson, R.; Bailey, S.; McBratney, A.B. Convolutional neural network for simultaneous prediction of several soil properties using visible/near-infrared, mid-infrared, and their combined spectra. Geoderma 2019, 352, 251–267. [Google Scholar] [CrossRef]
- Jin, J.; Pratama, B.A.; Wang, Q. Tracing leaf photosynthetic parameters using hyperspectral indices in an Alpine deciduous forest. Remote Sens. 2020, 12, 1124. [Google Scholar] [CrossRef] [Green Version]
- Jin, J.; Wang, Q.; Song, G. Selecting informative bands for partial least squares regressions improves their goodness-of-fits to estimate leaf photosynthetic parameters from hyperspectral data. Photosynth. Res. 2021, 1–12. [Google Scholar] [CrossRef]
- Reich, P.B.; Ellsworth, D.S.; Walters, M.B. Leaf structure (specific leaf area) modulates photosynthesis—nitrogen relations: Evidence from within and across species and functional groups. Funct. Ecol. 1998, 12, 948–958. [Google Scholar] [CrossRef]
- Chaves, A.R.M.; Ten-Caten, A.; Pinheiro, H.A.; Ribeiro, A.; Damatta, F.M. Seasonal changes in photoprotective mechanisms of leaves from shaded and unshaded field-grown coffee (Coffea arabica L.) trees. Trees-Struct. Funct. 2008, 22, 351–361. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K.; Buschmann, C.; Döll, M.; Fietz, H.J.; Bach, T.; Kozel, U.; Meier, D.; Rahmsdorf, U. Photosynthetic activity, chloroplast ultrastructure, and leaf characteristics of high-light and low-light plants and of sun and shade leaves. Photosynth. Res. 1981, 2, 115–141. [Google Scholar] [CrossRef]
- Niinemets, Ü.; Keenan, T.F.; Hallik, L. A worldwide analysis of within-canopy variations in leaf structural, chemical and physiological traits across plant functional types. New Phytol. 2015, 205, 973–993. [Google Scholar] [CrossRef] [Green Version]
- Niinemets, Ü.; Kull, O.; Tenhunen, J.D. Within-canopy variation in the rate of development of photosynthetic capacity is proportional to integrated quantum flux density in temperate deciduous trees. Plant Cell Environ. 2004, 27, 293–313. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Modell. 1999, 124, 99–119. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Chen, J.M.; Liu, J.; Black, T.A.; Croft, H.; Staebler, R.; He, L.; Arain, M.A.; Chen, B.; Mo, G.; et al. Comparison of big-leaf, two-big-leaf, and two-leaf upscaling schemes for evapotranspiration estimation using coupled carbon-water modeling. J. Geophys. Res. Biogeosci. 2018, 123, 207–225. [Google Scholar] [CrossRef]
- Dillen, S.Y.; de Beeck, M.O.; Hufkens, K.; Buonanduci, M.; Phillips, N.G. Seasonal patterns of foliar reflectance in relation to photosynthetic capacity and color index in two co-occurring tree species, Quercus rubra and Betula papyrifera. Agric. For. Meteorol. 2012, 160, 60–68. [Google Scholar] [CrossRef]
- Alton, P.B. Retrieval of seasonal Rubisco-limited photosynthetic capacity at global FLUXNET sites from hyperspectral satellite remote sensing: Impact on carbon modelling. Agric. For. Meteorol. 2017, 232, 74–88. [Google Scholar] [CrossRef] [Green Version]
- Croft, H.; Chen, J.M.; Luo, X.; Bartlett, P.; Chen, B.; Staebler, R.M. Leaf chlorophyll content as a proxy for leaf photosynthetic capacity. Glob. Chang. Biol. 2017, 23, 3513–3524. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F.; Cescatti, A.; Gitelson, A.A. Leaf chlorophyll constraint on model simulated gross primary productivity in agricultural systems. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 160–176. [Google Scholar] [CrossRef] [Green Version]
- Houborg, R.; Cescatti, A.; Migliavacca, M.; Kustas, W.P. Satellite retrievals of leaf chlorophyll and photosynthetic capacity for improved modeling of GPP. Agric. For. Meteorol. 2013, 117, 10–23. [Google Scholar] [CrossRef]
- Song, G.; Wang, Q.; Jin, J. Leaf photosynthetic capacity of sunlit and shaded mature leaves in a deciduous forest. Forests 2020, 11, 318. [Google Scholar] [CrossRef] [Green Version]
- Seo, Y.A.; Kim, K.R.; Cho, C.; Oh, J.W.; Kim, T.H. Deep neural network-based concentration model for oak pollen allergy warning in South Korea. Allergy Asthma Immunol. Res. 2020, 12, 149–163. [Google Scholar] [CrossRef]






| Traits | Period | R2 | RMSE | MAE | RPD |
|---|---|---|---|---|---|
| Vcmax | Flushing | 0.70 | 11.03 | 8.34 | 1.85 |
| Maturity | 0.48 | 12.53 | 9.39 | 1.41 | |
| Senescence | 0.52 | 8.05 | 6.33 | 1.46 | |
| Jmax | Flushing | 0.78 | 16.60 | 12.06 | 2.15 |
| Maturity | 0.50 | 19.68 | 15.18 | 1.43 | |
| Senescence | 0.55 | 18.84 | 15.04 | 1.47 |
| Leaf Type | DNN Model | Vcmax | Jmax | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | RPD | R2 | RMSE | MAE | RPD | ||
| All | ref, LT | 0.53 | 11.83 | 8.94 | 1.46 | 0.53 | 21.40 | 16.82 | 1.46 |
| ref, LMA | 0.54 | 11.24 | 8.58 | 1.47 | 0.53 | 21.21 | 16.53 | 1.46 | |
| ref, Chl | 0.54 | 11.73 | 8.90 | 1.47 | 0.55 | 20.92 | 16.27 | 1.49 | |
| ref, LT, Chl | 0.49 | 11.90 | 9.20 | 1.41 | 0.51 | 20.94 | 16.74 | 1.42 | |
| ref, LMA, Chl | 0.55 | 11.53 | 8.94 | 1.48 | 0.53 | 21.79 | 16.73 | 1.45 | |
| ref, LT, LMA, Chl | 0.54 | 11.70 | 9.24 | 1.44 | 0.51 | 22.67 | 17.46 | 1.41 | |
| Sunlit | ref, LT | 0.50 | 12.56 | 9.69 | 1.41 | 0.48 | 22.98 | 17.78 | 1.39 |
| ref, LMA | 0.50 | 12.36 | 9.69 | 1.42 | 0.49 | 22.12 | 17.27 | 1.40 | |
| ref, Chl | 0.54 | 11.55 | 9.28 | 1.49 | 0.52 | 19.96 | 16.87 | 1.45 | |
| ref, LT, Chl | 0.50 | 12.71 | 9.91 | 1.42 | 0.49 | 21.05 | 16.22 | 1.41 | |
| ref, LMA, Chl | 0.52 | 12.79 | 10.18 | 1.43 | 0.54 | 20.97 | 16.62 | 1.49 | |
| ref, LT, LMA, Chl | 0.53 | 12.44 | 9.88 | 1.45 | 0.50 | 21.53 | 16.66 | 1.40 | |
| Shaded | ref, LT | 0.42 | 7.07 | 5.37 | 1.29 | 0.36 | 14.38 | 11.66 | 1.20 |
| ref, LMA | 0.49 | 6.17 | 5.05 | 1.41 | 0.45 | 11.48 | 9.14 | 1.39 | |
| ref, Chl | 0.46 | 6.39 | 5.04 | 1.28 | 0.41 | 10.30 | 8.37 | 1.26 | |
| ref, LT, Chl | 0.44 | 6.84 | 5.64 | 1.30 | 0.37 | 12.05 | 7.73 | 1.22 | |
| ref, LMA, Chl | 0.47 | 6.49 | 5.50 | 1.39 | 0.43 | 9.34 | 7.99 | 1.38 | |
| ref, LT, LMA, Chl | 0.45 | 6.82 | 5.01 | 1.33 | 0.37 | 11.57 | 9.67 | 1.23 | |
| Period | DNN Model | Vcmax | Jmax | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | RPD | R2 | RMSE | MAE | RPD | ||
| Flushing | ref, LT | 0.73 | 11.18 | 8.63 | 1.93 | 0.78 | 17.68 | 12.89 | 2.07 |
| ref, LMA | 0.71 | 11.25 | 8.49 | 1.86 | 0.73 | 18.05 | 13.01 | 1.93 | |
| ref, Chl | 0.77 | 11.49 | 9.37 | 2.04 | 0.75 | 18.83 | 15.15 | 2.00 | |
| ref, LT, Chl | 0.64 | 12.19 | 9.48 | 1.86 | 0.75 | 17.71 | 12.50 | 1.92 | |
| ref, LMA, Chl | 0.82 | 10.64 | 9.43 | 2.26 | 0.79 | 17.17 | 13.56 | 2.13 | |
| ref, LT, LMA, Chl | 0.82 | 11.31 | 9.63 | 2.01 | 0.83 | 15.65 | 12.33 | 2.21 | |
| Maturity | ref, LT | 0.43 | 12.51 | 9.50 | 1.36 | 0.48 | 21.84 | 16.92 | 1.41 |
| ref, LMA | 0.49 | 11.89 | 9.24 | 1.45 | 0.49 | 21.79 | 16.70 | 1.40 | |
| ref, Chl | 0.41 | 12.22 | 9.79 | 1.33 | 0.49 | 21.57 | 16.84 | 1.41 | |
| ref, LT, Chl | 0.48 | 12.15 | 10.04 | 1.41 | 0.46 | 21.63 | 17.71 | 1.39 | |
| ref, LMA, Chl | 0.46 | 11.90 | 10.68 | 1.42 | 0.49 | 20.14 | 16.23 | 1.43 | |
| ref, LT, LMA, Chl | 0.44 | 12.43 | 9.98 | 1.39 | 0.52 | 20.09 | 16.36 | 1.45 | |
| Senescence | ref, LT | 0.49 | 8.24 | 6.56 | 1.42 | 0.52 | 19.31 | 15.45 | 1.44 |
| ref, LMA | 0.48 | 8.42 | 6.78 | 1.40 | 0.56 | 18.89 | 14.77 | 1.50 | |
| ref, Chl | 0.56 | 7.84 | 6.03 | 1.52 | 0.54 | 19.16 | 15.07 | 1.47 | |
| ref, LT, Chl | 0.53 | 8.18 | 6.23 | 1.49 | 0.59 | 18.56 | 14.59 | 1.53 | |
| ref, LMA, Chl | 0.51 | 8.40 | 6.67 | 1.43 | 0.53 | 18.58 | 15.14 | 1.46 | |
| ref, LT, LMA, Chl | 0.47 | 9.37 | 7.19 | 1.42 | 0.61 | 17.67 | 14.14 | 1.62 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, G.; Wang, Q. Including Leaf Traits Improves a Deep Neural Network Model for Predicting Photosynthetic Capacity from Reflectance. Remote Sens. 2021, 13, 4467. https://doi.org/10.3390/rs13214467
Song G, Wang Q. Including Leaf Traits Improves a Deep Neural Network Model for Predicting Photosynthetic Capacity from Reflectance. Remote Sensing. 2021; 13(21):4467. https://doi.org/10.3390/rs13214467
Chicago/Turabian StyleSong, Guangman, and Quan Wang. 2021. "Including Leaf Traits Improves a Deep Neural Network Model for Predicting Photosynthetic Capacity from Reflectance" Remote Sensing 13, no. 21: 4467. https://doi.org/10.3390/rs13214467
APA StyleSong, G., & Wang, Q. (2021). Including Leaf Traits Improves a Deep Neural Network Model for Predicting Photosynthetic Capacity from Reflectance. Remote Sensing, 13(21), 4467. https://doi.org/10.3390/rs13214467