Lithological Mapping Based on Fully Convolutional Network and Multi-Source Geological Data
Abstract
:1. Introduction
2. Methods
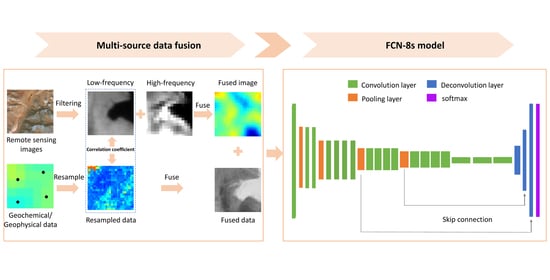
2.1. Multi-Source Data Fusion
2.2. Fully Convolutional Network
- (1)
- Deconvolution network
- (2)
- Skip connection
2.3. Workflow and FCN Model Architecture
2.4. Model Evaluation Metrics
3. Case Study
3.1. Geological Setting
3.2. Data and Preprocessing
3.3. Building of Training Datasets
4. Results
4.1. Model Training
4.2. Lithological Mapping
5. Discussion
6. Conclusions
- (1)
- The multi-source data fusion technology integrates ASTER remote sensing images, geochemical exploration data, PALSAR DEM data, and aeromagnetic data at various scales, providing a comprehensive analysis of geodata rather than a single type of data resource.
- (2)
- FCN is a specially designed semantic segmentation model that dominates in end-to-end and pixel-wise prediction with an arbitrary input size. FCN retains the advantages of feature extraction in CNN and solves the problem of classifying each pixel in an image through deconvolution operations and skip connections, making it an innovative alternative for lithological mapping.
- (3)
- A comparative study was carried out, proving that the proposed framework is effective and successful in geological feature mapping from the viewpoints of vision and quantification. The proposed FCN-8s model increased the classification accuracy of leucogranites by 9% compared to that reported in previous studies by extracting deeper-level hidden information from multi-source data.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harris, J.R.; Grunsky, E.C. Predictive lithological mapping of Canada’s North using Random Forest classification applied to geophysical and geochemical data. Comput. Geosci. 2015, 80, 9–25. [Google Scholar] [CrossRef]
- Othman, A.A.; Gloaguen, R. Integration of spectral, spatial and morphometric data into lithological mapping: A comparison of different Machine Learning Algorithms in the Kurdistan Region, NE Iraq. J. Asian Earth Sci. 2017, 146, 90–102. [Google Scholar] [CrossRef]
- Pal, M.; Rasmussen, T.; Porwal, A. Optimized lithological mapping from multispectral and hyperspectral remote sensing images using fused multi-classifiers. Remote Sens. 2020, 12, 177. [Google Scholar] [CrossRef] [Green Version]
- Shirmard, H.; Farahbakhsh, E.; Muller, D.; Chandra, R. A review of machine learning in processing remote sensing data for mineral exploration. arXiv 2021, arXiv:2103.07678. [Google Scholar] [CrossRef]
- Wang, Z.; Zuo, R.; Jing, L. Fusion of Geochemical and Remote-Sensing Data for Lithological Mapping Using Random Forest Metric Learning. Math. Geosci. 2021, 53, 1125–1145. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Zuo, R.; Xiong, Y.; Wang, J.; Carranza, E.J.M. Deep learning and its application in geochemical mapping. Earth-Sci. Rev. 2019, 192, 1–14. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Zuo, R. Recognizing multivariate geochemical anomalies for mineral exploration by combining deep learning and one-class support vector machine. Comput. Geosci. 2020, 140, 104484. [Google Scholar] [CrossRef]
- Xiong, Y.; Zuo, R. Robust Feature Extraction for Geochemical Anomaly Recognition Using a Stacked Convolutional Denoising Autoencoder. Math. Geosci. 2021. [Google Scholar] [CrossRef]
- Li, T.; Zuo, R.; Xiong, Y.; Peng, Y. Random-drop data augmentation of deep convolutional neural network for mineral prospectivity mapping. Nat. Resour. Res. 2021, 30, 27–38. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.; Liu, C.; Wang, Y. Mineral Prospectivity Prediction via Convolutional Neural Networks Based on Geological Big Data. J. Earth Sci. 2021, 32, 327–347. [Google Scholar] [CrossRef]
- Luo, Z.; Zuo, R.; Xiong, Y.; Wang, X. Detection of geochemical anomalies related to mineralization using the GANomaly network. Appl. Geochem. 2021, 131, 105043. [Google Scholar] [CrossRef]
- Deng, L.; Yu, D. Deep learning: Methods and applications. Found. Trends Signal Process. 2014, 7, 197–387. [Google Scholar] [CrossRef] [Green Version]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, C.; Zuo, R.; Xiong, Y. Detection of the multivariate geochemical anomalies associated with mineralization using a deep convolutional neural network and a pixel-pair feature method. Appl. Geochem. 2021, 130, 104994. [Google Scholar] [CrossRef]
- Zhang, S.; Carranza, E.J.M.; Wei, H.; Xiao, K.; Yang, F.; Xiang, J.; Zhang, S.; Xu, Y. Data-driven mineral prospectivity mapping by joint application of unsupervised convolutional auto-encoder network and supervised convolutional neural network. Nat. Resour. Res. 2021, 30, 1011–1031. [Google Scholar] [CrossRef]
- Sherrah, J. Fully convolutional networks for dense semantic labelling of high-resolution aerial imagery. arXiv 2016, arXiv:1606.02585. [Google Scholar]
- Zuo, R. Geodata science-based mineral prospectivity mapping: A review. Nat. Resour. Res. 2020, 29, 3415–3424. [Google Scholar] [CrossRef]
- Zuo, R.; Xiong, Y. Geodata science and geochemical mapping. J. Geochem. Explor. 2020, 209, 106431. [Google Scholar] [CrossRef]
- Ge, W.; Cheng, Q.; Tang, Y.; Jing, L.; Gao, C. Lithological classification using sentinel-2A data in the Shibanjing ophiolite complex in inner Mongolia, China. Remote Sens. 2018, 10, 638. [Google Scholar] [CrossRef] [Green Version]
- Brandmeier, M.; Chen, Y. Lithological classification using multi-sensor data and convolutional neural networks. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 55–59. [Google Scholar] [CrossRef] [Green Version]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.; Anders, K.; Gloaguen, R.; et al. Multisource and multitemporal data fusion in remote sensing: A comprehensive review of the state of the art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef] [Green Version]
- Thiele, S.T.; Lorenz, S.; Kirsch, M.; Acosta, I.C.C.; Tusa, L.; Herrmann, E.; Möckel, R.; Gloaguen, R. Multi-scale, multi-sensor data integration for automated 3-D geological mapping. Ore Geol. Rev. 2021, 136, 104252. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef] [Green Version]
- Shelhamer, E.; Long, J.; Darrell, T. Fully convolutional neural networks for semantic segmentation. arXiv 2016, arXiv:1605.06211. [Google Scholar]
- Fu, G.; Liu, C.; Zhou, R.; Sun, T.; Zhang, Q. Classification for high resolution remote sensing imagery using a fully convolutional network. Remote Sens. 2017, 9, 498. [Google Scholar] [CrossRef] [Green Version]
- Zou, L.; Zhu, X.; Wu, C.; Liu, Y.; Qu, L. Spectral–spatial exploration for hyperspectral image classification via the fusion of fully convolutional networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 659–674. [Google Scholar] [CrossRef]
- Wang, J.; Song, L.; Li, Z.; Sun, H.; Sun, J.; Zheng, N. End-to-end object detection with fully convolutional network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 20–25 June 2021; pp. 15849–15858. [Google Scholar]
- Ding, H.; Jing, L.; Li, H.; Tang, Y.; Ma, H.; Zhu, B.; Wang, W.; Qiu, L. A method and system for improving the resolution of geochemical layers. Chinese Patents No. 201811275285.4, 28 August 2020. [Google Scholar]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Fully convolutional neural networks for remote sensing image classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5071–5074. [Google Scholar] [CrossRef] [Green Version]
- He, C.; He, B.; Tu, M.; Wang, Y.; Qu, T.; Wang, D.; Liao, M. Fully convolutional networks and a manifold graph embedding-based algorithm for polsar image classification. Remote Sens. 2020, 12, 1467. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 1520–1528. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Pan, J.; Lai, W.; Lau, R.W.; Yang, M. Learning fully convolutional networks for iterative non-blind deconvolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3817–3825. [Google Scholar] [CrossRef] [Green Version]
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond accuracy, F-score and ROC: A family of discriminant measures for performance evaluation. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Hobart, TAS, Australia, 4–8 December 2006; Springer: Berlin/Heidelberg, Germany; pp. 1015–1021. [Google Scholar] [CrossRef] [Green Version]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Rahman, M.A.; Wang, Y. Optimizing intersection-over-union in deep neural networks for image segmentation. In Proceedings of the International Symposium on Visual Computing, Las Vegas, NV, USA, 12–14 December 2006; Springer: Cham, Germany, 10 December 2016; pp. 234–244. [Google Scholar] [CrossRef]
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized intersection over union: A metric and a loss for bounding box regression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 658–666. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Liu, Z.; Liu, X.; Ji, W. Himalayan leucogranite: Petrogenesis and implications to orogenesis and plateau uplift. Acta Petrol. Sin. 2015, 31, 1–36. [Google Scholar]
- Wu, F.; Liu, X.; Ji, W.; Wang, J.; Yang, L. Highly fractionated granites: Recognition and research. Sci. China Earth Sci. 2017, 60, 1201–1219. [Google Scholar] [CrossRef]
- Wang, R.; Wu, F.; Xie, L.; Liu, X.; Wang, J.; Yang, L.; Lai, W.; Liu, C. A preliminary study of rare-metal mineralization in the Himalayan leucogranite belts, South Tibet. Sci. China Earth Sci. 2017, 60, 1655–1663. [Google Scholar] [CrossRef]
- Xie, L.; Tao, X.; Wang, R.; Wu, F.; Liu, C.; Liu, X.; Li, X.; Zhang, R. Highly fractionated leucogranites in the eastern Himalayan Cuonadong dome and related magmatic Be–Nb–Ta and hydrothermal Be–W–Sn mineralization. Lithos 2020, 354, 105286. [Google Scholar] [CrossRef]
- Wu, F.; Liu, X.; Liu, Z.; Wang, R.; Xie, L.; Wang, J.; Ji, W.; Yang, L.; Liu, C.; Khanal, G.P. Highly fractionated Himalayan leucogranites and associated rare-metal mineralization. Lithos 2020, 352, 105319. [Google Scholar] [CrossRef]
- Cao, H.; Li, G.; Zhang, Z.; Zhang, L.; Dong, S.; Xia, X.; Liang, W.; Fu, J.; Huang, Y.; Xiang, A. Miocene Sn polymetallic mineralization in the Tethyan Himalaya, southeastern Tibet: A case study of the Cuonadong deposit. Ore Geol. Rev. 2020, 119, 103403. [Google Scholar] [CrossRef]
- Xiang, A.; Li, W.; Li, G.; Dai, Z.; Yu, H.; Yang, F. Mineralogy, isotope geochemistry and ore genesis of the miocene Cuonadong leucogranite-related Be-W-Sn skarn deposit in Southern Tibet. J. Asian Earth Sci. 2020, 196, 104358. [Google Scholar] [CrossRef]
- Fu, J.; Li, G.; Wang, G.; Zhang, L.; Liang, W.; Zhang, X.; Jiao, Y.; Huang, Y. Structural and thermochronologic constraints on skarn rare-metal mineralization in the Cenozoic Cuonadong Dome, Southern Tibet. J. Asian Earth Sci. 2021, 205, 104612. [Google Scholar] [CrossRef]
- Li, G.; Zhang, L.; Jiao, Y.; Xia, X.; Dong, S.; Fu, J.; Liang, W.; Zhang, Z.; Wu, J.; Dong, L. First discovery and implications of Cuonadong superlarge Be-W-Sn polymetallic deposit in Himalayan metallogenic belt, southern Tibet. Miner. Depos. 2017, 36, 1003–1008. [Google Scholar]
- Liang, W.; Li, G.; Zhang, L.; Fu, J.; Zhang, Z. Cuonadong Be-rare polymetallic metal deposit: Constraints from Ar-Ar age of hydrothermal muscovite. Sediment. Geol. Tethyan Geol. 2020, 40, 76–81. [Google Scholar]
- Cao, H.; Li, G.; Zhang, R.; Zhang, Y.; Zhang, L.; Dai, Z.; Zhang, Z.; Liang, W.; Dong, S.; Xia, X. Genesis of the Cuonadong tin polymetallic deposit in the Tethyan Himalaya: Evidence from geology, geochronology, fluid inclusions and multiple isotopes. Gondwana Res. 2021, 92, 72–101. [Google Scholar] [CrossRef]
- Xie, J.; Qiu, H.; Bai, X.; Zhang, W.; Wang, Q.; Xia, X. Geochronological and geochemical constraints on the Cuonadong leucogranite, eastern Himalaya. Acta Geochim. 2018, 37, 347–359. [Google Scholar] [CrossRef]
- Xia, X.; Li, G.; Cao, H.; Liang, W.; Fu, J. Petrogenic Age and Geochemical Characteristics of the Mother Rock of Skarn Type Ore Body in the Cuonadong Be-W-Sn Polymetallic Deposit, Southern Tibet. Earth Sci. 2019, 44, 2207–2223. [Google Scholar]
- Huang, Y.; Fu, J.; Li, G.; Zhang, L.; Liu, H. Determination of Lalong Dome in South Tibet and New Discovery of Rare Metal Mineralization. Earth Sci. 2019, 44, 2197–2206. [Google Scholar]
- Jiao, Y.; Huang, X.; Li, G.; Liang, S.; Guo, J. Deep Structure and Mineralization of Zhaxikang Ore-Concentration Area, South Tibet: Evidence from Geophysics. Earth Sci. 2019, 44, 2117–2128. [Google Scholar]
- Jiao, Y.; Huang, X.; Liang, S.; Zhang, Z.; Li, G. Deep structure and prospecting significance of the Cuonadong dome, Tethys Himalaya, China: Geophysical constraints. Geol. J. 2021, 56, 253–264. [Google Scholar] [CrossRef]
- Xie, X.; Mu, X.; Ren, T. Geochemical mapping in China. J. Geochem. Explor. 1997, 60, 99–113. [Google Scholar]
- Aitchison, J. The statistical analysis of compositional data. J. R. Stat. Soc. Ser. B (Methodol.) 1982, 44, 139–160. [Google Scholar] [CrossRef]
- Zuo, R.; Xia, Q.; Wang, H. Compositional data analysis in the study of integrated geochemical anomalies associated with mineralization. Appl. Geochem. 2013, 28, 202–211. [Google Scholar] [CrossRef]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1139–1147. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Parsa, M.; Maghsoudi, A.; Yousefi, M. Spatial analyses of exploration evidence data to model skarn-type copper prospectivity in the Varzaghan district, NW Iran. Ore Geol. Rev. 2018, 92, 97–112. [Google Scholar] [CrossRef]
- Wang, Z.; Zuo, R.; Dong, Y. Mapping of himalaya leucogranites based on ASTER and sentinel-2A datasets using a hybrid method of metric learning and random forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1925–1936. [Google Scholar] [CrossRef]
- Wang, Z.; Zuo, R.; Dong, Y. Mapping Himalayan leucogranites using a hybrid method of metric learning and support vector machine. Comput. Geosci. 2020, 138, 104455. [Google Scholar] [CrossRef]











| Layer Name | Number | Filter Size | Feature Dimensions |
|---|---|---|---|
| Input | 256 × 256 × 1 | ||
| Conv1 | 2 | 3 × 3 | 256 × 256 × 64 |
| Pool1 | 1 | 2 × 2 | 128 × 128 × 64 |
| Conv2 | 2 | 3 × 3 | 128 × 128 × 128 |
| Pool2 | 1 | 2 × 2 | 64 × 64 × 128 |
| Conv3 | 4 | 3 × 3 | 64 × 64 × 256 |
| Pool3 | 1 | 2 × 2 | 32 × 32 × 256 |
| Conv4 | 4 | 3 × 3 | 32 × 32 × 512 |
| Pool4 | 1 | 2 × 2 | 16 × 16 × 512 |
| Conv5 | 4 | 3 × 3 | 16 × 16 × 512 |
| Pool5 | 1 | 2 × 2 | 8 × 8 × 512 |
| Conv6 | 1 | 1 × 1 | 8 ×8 × 4096 |
| Dropout | 8 ×8 × 4096 | ||
| Conv7 | 1 | 1 × 1 | 8 ×8 × 4096 |
| Conv8 | 1 | 1 × 1 | 8 × 8 × 4096 |
| tConv1 | 1 | 2 × 2 | 16 × 16 × 512 |
| tConv2 | 1 | 2 × 2 | 32 × 32 × 256 |
| tConv3 | 1 | 8 × 8 | 256 × 256 × 2 |
| Softmax | |||
| Output | 256 × 256 × 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zuo, R.; Liu, H. Lithological Mapping Based on Fully Convolutional Network and Multi-Source Geological Data. Remote Sens. 2021, 13, 4860. https://doi.org/10.3390/rs13234860
Wang Z, Zuo R, Liu H. Lithological Mapping Based on Fully Convolutional Network and Multi-Source Geological Data. Remote Sensing. 2021; 13(23):4860. https://doi.org/10.3390/rs13234860
Chicago/Turabian StyleWang, Ziye, Renguang Zuo, and Hao Liu. 2021. "Lithological Mapping Based on Fully Convolutional Network and Multi-Source Geological Data" Remote Sensing 13, no. 23: 4860. https://doi.org/10.3390/rs13234860
APA StyleWang, Z., Zuo, R., & Liu, H. (2021). Lithological Mapping Based on Fully Convolutional Network and Multi-Source Geological Data. Remote Sensing, 13(23), 4860. https://doi.org/10.3390/rs13234860