1. Introduction
Tomographic Synthetic Aperture Radar (TomoSAR) achieves the elevation resolution of layover targets through multi-angle observation of the same observation scene. TomoSAR has become an advanced data collection tool for three-dimentional (3D) applications such as topographic surveying, urban surveillance, biomass estimation, cultural heritage assets, and monitoring of slow-moving landslides [
1,
2,
3,
4,
5].
In 1995, the TomoSAR 3D imaging technology was demonstrated for the first time, which was of great significance in promoting the development of TomoSAR [
6]. In 2006, Fornaro et al. provided the first validation of spaceborne long-term SAR tomography. Specially, the 3D imaging results from European Remote Sensing 1 and 2 (ERS-1 and ERS-2) satellites over the urban area of Napoli were presented [
7]. Later, the high-resolution spaceborne SAR systems such as TerraSAR-X [
8] and Cosmo-Skymed [
9] were launched. With the acquisition of high-resolution TomoSAR data, there are many achievements regarding TomoSAR 3D reconstruction. TomoSAR 3D reconstruction mainly consists of two steps, including point cloud generation and point cloud processing. For the former, the mainstream methods are based on Compressive Sensing (CS). For the latter, the method of the human-made buildings has been hot research. Initially, most of methods based on the hypothesis of polyhedral building structure were demonstrated [
10,
11,
12]. Considering the more complex buildings containing curved structures, methods for curved structures are required. Zhu et al. proposed a method suitable for the buildings with rectangular footprints and curved footprints [
13]. In this method, the façade points are clustered into individual facades by K-means, and then the segmented plane or curved surface are further modeled and merged. Subsequently, Shahzad et al. proposed a robust reconstruction method for larger areas [
14]. In this method, three-step automatic clustering (TSAC) is proposed to segment the building facades [
15]. This method integrates the advantages of Density-Based Spatial Clustering of Applications with Noise (DBSCAN) and Mean Shift (MS).
Although the TomoSAR technologies have been well developed, there are several shortcomings in the spaceborne TomoSAR. First, due to the long revisit time, the spaceborne TomoSAR suffers from the problem of temporal decorrelation, especially for mountains with many distributed targets [
16]. Second, the satellites only work on the ascending and descending orbits, which is not conducive to adjusting the observation trajectory [
13]. Third, the spaceborne TomoSAR is inflexible and cannot respond quickly to the observation needs of a specific region. The airborne array TomoSAR can well address these problems by arranging the antenna array in the cross-track direction. The array TomoSAR system allows the acquisition of high-precision data for 3D mountain reconstruction [
17,
18]. The National Key Laboratory of Microwave Imaging Technology, Aerospace Information Research Institute, Chinese Academy of Sciences (AIRCAS), has developed the first airborne array TomoSAR system in China. In 2015 and 2019, two experiments based on this system were successfully conducted over both urban areas and mountain areas. Furthermore, a series of TomoSAR point cloud processing methods have been proposed and validated by the airborne array TomoSAR data. In 2017, Gaussian Mixture Model (GMM) was applied for TomoSAR 3D point cloud processing [
19]. The GMM fully considers the distribution feature, and allows classification based on probability [
20]. In 2019, Zhou et al. proposed an automatic method using neural networks to regularize the 3D building structures [
21]. In 2020, Jiao et al. demonstrated the 3D reconstruction framework of buildings [
22]. Moreover, driven by this advanced single-pass mode, the multiple scattering of TomoSAR building point cloud has been interpreted and applied to high precision 3D reconstruction [
23,
24].
However, there are few literatures on TomoSAR 3D mountain reconstruction. The 3D mountain model is relevant in many fields, such as global mapping, disaster assessment, and disaster relief. Due to the layover phenomenon, mapping in high mountain areas remains a difficult task. Motivated by these chances and needs, 3D mountain reconstruction based on the airborne array TomoSAR is meaningful. The mountain point cloud can be obtained by referring to the mainstream CS-based methods. When the elevation span of the scene is larger than the ambiguous elevation of the TomoSAR system, the restricted isometry property (RIP) criterion is not satisfied. The original point cloud is aliased in the elevation direction [
25]. For low targets such as buildings, the elevation span of the scene can be known in advance. Therefore, the problem of elevation ambiguity can be solved by encrypting the baseline at the system level [
26]. Notwithstanding, the mountainous terrain is highly undulating. It is difficult to know the elevation span in advance. It is a challenge to solve the problem of elevation ambiguity at the system level. In addition, there is a trade-off between the ambiguous elevation and the elevation resolution. Even if the ambiguous elevation meets the requirements that no elevation ambiguity occurs in the original point cloud, the elevation resolution may be reduced. Limited by the system parameters and the characteristics of the scene, the TomoSAR mountain point cloud has the problem of elevation ambiguity.
Due to elevation ambiguity, none of the existing TomoSAR point cloud processing methods can be directly applied to TomoSAR mountain point cloud processing. To overcome the problem, an elevation ambiguity resolution method is proposed in this paper. The main purpose of elevation ambiguity resolution is to move the points to the correct elevation position. Obviously, it is not optimal to estimate the elevation ambiguity number point by point. Inspired by the processing methods of buildings, segmentation can improve the efficiency of elevation ambiguity resolution by converting the point processing to category processing. Consequently, segmentation and reorganization are the two steps of the proposed method. Notably, due to the common influence of elevation ambiguity and layover, the original point cloud may be corrupted by intersection, which will increase the difficulty of segmentation. In the first step, the difficulty of segmentation can be well addressed by using DBSCAN and GMM jointly. In the reorganization step, the segmentation results are rearranged in the elevation direction by elevation extension and combination, and the real point cloud is further automatically extracted by geometric constraints. The main contributions are as follows:
- (1)
A robust segmentation method combing DBSCAN and GMM is proposed. Compared with the traditional segmentation methods, the proposed method provides better segmentation of the TomoSAR mountain point cloud with intersection.
- (2)
Motivated by segmentation, an ingenious reorganization method is given. Through elevation extension and combination, reorganization allows to construct all possible results of elevation ambiguity resolution instead of estimating the elevation ambiguity number point by point.
- (3)
By analyzing the distribution law of TomoSAR point cloud, geometric constraints are given to ensure the automatic extraction of the real point cloud. If geometric constraints are not used, the processor needs to interpret and judge one by one from all the reorganization results.
This paper is organized as follows.
Section 2 briefly introduces our airborne array TomoSAR system.
Section 3 analyzes the difficulties in solving the elevation ambiguity problem. Furthermore, the distribution law of TomoSAR point cloud is demonstrated. In
Section 4, the proposed method for elevation ambiguity resolution is introduced in detail. In
Section 5, the processing results for both simulated data and real data are presented and quantitatively analyzed. As a comparison, the results of traditional methods are given. Besides, the 3D reconstruction results of airborne array TomoSAR are evaluated in detail on three kinds of external data, i.e., the optical image, AW3D30 DSM, and 1:10,000 DEM. Conclusions are given in
Section 6.
2. Array TomoSAR System
Because of the problem of temporal decorrelation caused by long revisit time, the traditional TomoSAR systems with repeat-pass cannot obtain a well-focused point cloud in the elevation direction, especially for mountains. The first domestic airborne array TomoSAR system is established by AIRCAS. With the application of multiple input multiple output technology, this system allows multi-angle data acquisition in a single flight by adding antennas in the cross-track direction. The rigid antenna array with a weight of 150 kg is used to ensure the stability of the baseline. Besides, a millimeter-level high-precision calibration system is adopted to record the actual route position, which provides a foundation for motion compensation and image registration. The system combines the advantages of elevation solution and high-precision coherent measurement, filling the gap of TomoSAR system in the field of 3D mountain reconstruction.
In 2019, our team conducted a flight experiment in Huangniba mountain area, Leshan, China. The 3D observation geometry of the airborne array TomoSAR is shown in
Figure 1. There are two cylindrical coordinate systems, i.e., the radar coordinate system
and the geodetic coordinate system
. Axes
a,
r, and
s indicate the azimuth direction, the range direction, and the elevation direction in turn, and they are orthogonal to each other. Similarly, axes
x,
y, and
z indicate the azimuth direction, the ground direction, and the height direction in turn, and they are orthogonal to each other. The antenna array is mounted on the lower abdomen of the aircraft. The system operates at X-band and adopts the right-side view mode observing from west to east. The aircraft flies at an altitude height of 3.5 km. The antenna width in the azimuth direction is 0.24 m, and the signal bandwidth is 500 MHz, which ensures that the azimuth resolution and range resolution are 0.12 m and 0.3 m, respectively. The baseline interval is 0.2 m. The detailed information of the system parameters is listed in
Table 1.
The function of the TomoSAR system ambiguous elevation [
27] is given by:
where
is the wavelength.
Referring to the flight experiments, let the incidence angle
vary from
to
and the scene height vary from 600 m to 1200 m. The ambiguous elevation map of our system is shown in
Figure 2. It can be seen that the ambiguous elevation of the TomoSAR system is determined by the incidence angle and the height of the observation scene. For the test parameter setting, the maximum ambiguous elevation is 352 m, which is smaller than the scene span. This reveals that the original point cloud will be corrupted by elevation ambiguity.
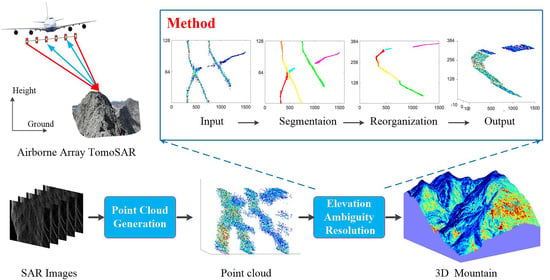
The process of 3D mountain reconstruction using the airborne array TomoSAR is shown in
Figure 3. It can be seen that elevation ambiguity resoltion is a necessary step for TomoSAR 3D mountain recontruction. In the following sections, the distribution law of TomoSAR point cloud will be discussed. Furthermore, the proposed elevation ambiguity resolution method and the experimental results will be introduced in detail.
3. Distribution Law of TomoSAR Point Cloud
In this section, the geometric distortion caused by TomoSAR side-view observation is first illustrated. Then, the CS-based layover solution is given. Furthermore, the cause of the elevation ambiguity problem, as well as the problems of intersection and hole in the original point cloud are explained. At last, the distribution law of TomoSAR point cloud is summarized.
3.1. Geometric Distortion
Radar exploits the time required for the electromagnetic wave to go back and forth to the target to measure the range. Under the far-field assumption, the electromagnetic wave can be regarded as a plane wave. For flat ground, the range increases with the ground range. There is only one echo of the scattering center in an azimuth-range unit. However, for uneven surfaces, geometric distortion may occur.
There are three kinds of geometric distortion in SAR images, including foreshortening, layover, and shadowing [
28]. The schematic of geometric distortion is shown in sequence in
Figure 4, where
S indicates the location of radar sensor,
indicates the incidence angle, and the red solid line indicates the imaging plane of the observed scene. Foreshortening means that the length of the range displayed on the SAR image is shorter than its real length. As shown in
Figure 4a, when the front slope (
: along the projection direction of the SAR beam) is less than the incidence angle
or the back slope (
: opposite to the projection direction of the SAR beam) is less than
, foreshortening occurs. In this case, the front slope shrinks more severely than the back slope. As shown in
Figure 4b, layover refers to the phenomenon that the range of the top is smaller than the range of the bottom on the SAR image. This is mainly because the front slope is greater than the incidence angle. In this case, the incident wave first reaches the top and then reaches the bottom. On the imaging plane,
and
are the starting and ending range of a layover region, respectively. As a result, multiple targets with different elevations fall in one azimuth-range unit. Moreover, the electromagnetic wave propagates in a straight line. As shown in
Figure 4c, when
, there is a section of terrain (
) behind the front slope that the radar beam cannot reach, and there will be no radar echo. In this case, there is a dark area in the corresponding position of the image (
), i.e., shadowing occurs.
3.2. Compressive Sensing-Based Layover Solution
TomoSAR can extend the 2D SAR image to the third elevation dimension through multi-angle observation. The observation geometry on the ground-height plane of the airborne array TomoSAR is shown in
Figure 5, where the terrain marked as dark red can be illuminated, and the terrain marked as black indicates the shadowing area. Moreover, the three targets
,
and
are layover in an azimuth-range unit. To rebuild them, the pixel value of the complex image can be expressed in the form of superposition of multiple frequency component signals [
29]:
where
,
is the overall baseline length,
is the elevation span of the illuminated layover terrain,
is the 3D scattering coefficient.
Under far-field approximation, the range function can be expanded in the Taylor series as follows:
Discarding
, (
2) can be written as:
where
Note that the elevation
s and the antenna
constitute a Fourier pair. Thus,
can be estimated through an inverse Fourier transform operator. However, this operation requires the baseline to be evenly distributed. Moreover, the Nyquist sampling theorem illustrates that the elevation resolution of the limited number of baselines is limited. Compressed sensing theory can break through the above limitations. If
can be expressed by the sparsity basis
, (
4) can be written as:
where
is the column vector with K-nonzero elements,
is the sparsity sparsis matrix, that is usually expressed as identity matrix, and
N is the discrete number in a
period.
The generic element of the measurement matrix
is defined as:
where
.
If the signal is K sparse in elevation, and the measurement matrix
satisfies the RIP, the optimal solution of
K non-zero coefficients can be obtained through
M measured values.The layover solution can be acquired by solving an
-norm minimization problem:
3.3. Cause of Elevation Ambiguity
Generally, the flat-earth phase between channels is compensated before the generation of point cloud. Therefore, the elevation of ground is zero, and the elevation of the targets on the ground is the relative elevation to the ground. Thus, the original point cloud of regular buildings is distributed in a Z shape [
24]. However, for the mountain area with undulating terrain, the elevation of the original point cloud no longer increases monotonically with the ground.
In fact, the phase difference between two adjacent channels
is a variable related to the incidence angle. That is because the horizontal baseline between the adjacent channels can be expressed as:
where
is the horizontal angle of the baseline
b.
If the flat-earth phase compensation is not done, then the elevation of targets can be expressed as
Discarding the constant variable
, the above formula can be written as:
Thus, there is a positive correlation relationship between the elevation and the incidence angle. This relationship is called positive correlation constraint in the following. Although the terrain is undulating, the elevation of the point cloud will monotonically increase with the ground.
For the mountain scene shown in
Figure 5, the elevation span is
, where
is the incidence angle of
, and
is the incidence angle of
. Based on the spectral estimation, the estimated elevation of the target with the true elevation value
is:
where
d is the number of elevation ambiguity. When the scene span is greater than the ambiguous elevation of the system,
d is not equal to zero. As a result, the points outside the elevation period will be aliased in the elevation direction.
The schematic diagram of the elevation ambiguity of layover targets is illustrated in
Figure 6. Assuming that
is located at the origin of the coordinates, i.e., the elevation value of
is zero. Because of elevation ambiguity, only the point
in the main period can be correctly sampled, and the points
and
outside the main period are aliased. The elevation value of
is shifted upward for one period, corresponding to
. Furthermore, the elevation value of
is shifted downward for one period, corresponding to
. Besides, the elevation difference between
and
is an integer multiple of the ambiguous elevation. In the original point cloud,
and
will intersect at one point.
3.4. Distribution Law of TomoSAR Point Cloud
Considering the positive correlation constraint and the illumination geometric constraint [
30], the real point cloud distribution law is summarized as follows:
- (1)
The real point cloud satisfies the boundary constraint in the elevation direction. There is a monotonic increasing relationship between the elevation and ground. Therefore, the elevation values of the points without elevation ambiguity are all within the upper and lower elevation boundaries. As shown in
Figure 5, the incidence angle of points
to
increases with the ground. According to (
11), the elevation values of points
to
increase with the ground. Using the reduction to absurdity, if the elevation value does not increase with the ground distance,
will be illuminated. Since
is located in the shadow area, it cannot be illuminated;
- (2)
The real point cloud satisfies the elevation continuity constraint. If there is no shadowing, the elevation continuously increases. Otherwise, holes will be included in the point cloud. However, the near end and the far end of the hole area have equal elevation values. As shown in
Figure 5, there is a shadowing between
and
. The incidence angles of points
and
are the same. In the same way, the elevation values of points
and
are the same. Thus, the elevation continuity of the real point cloud is always satisfied.
The distribution law of the original point cloud with elevation ambiguity is summarized as follows:
- (1)
The elevation difference between the real target and the ambiguity target is an integer multiple of the discrete numbers in an elevation period;
- (2)
The layover points whose elevation difference is an integer multiple of the discrete number will intersect;
- (3)
For the points in the same period, the elevation is increasing, and the elevation ambiguity number is equal;
- (4)
The elevation values of the points at the near end and the far end of the hole area are continuous.
In summary, the TomoSAR mountain point cloud is affected by geometric distortion and elevation ambiguity. The former is an inherent problem of side-viewing TomoSAR. The latter appears when the elevation span of the illuminated scene is greater than the ambiguous elevation of the TomoSAR system. The intersection is caused by elevation ambiguity and terrain layover. Based on the positive correlation constraint and the illumination geometric constraint, the real point cloud satisfies the boundary constraint and elevation continuity constraint. It is worth emphasizing that the two constrains are not impacted by holes caused by shadowing.
4. The Segmentation and Reorganization-Based Method
In this section, the proposed elevation ambiguity resolution method based on segmentation and reorganization of TomoSAR point cloud is introduced in detail. The workflow of the proposed method is shown in
Figure 7.
4.1. Segmentation
The purpose of segmentation is to cluster the points with the same elevation ambiguity number into one category. Segmentation allows the dimensionality reduction from point to category. This idea cannot only improve the efficiency, but also increase the accuracy of the results from a statistical perspective. Considering the outliers and the intersection, the segmentation method combining DBSCAN and GMM is proposed.
First, DBSCAN is performed for all points. Considering the high anisotropy of the positioning error of TomoSAR points, vortex instead of sphere is adopted to determine the neighborhood. By setting the size of vortex and the minimum number of points to be involved in the vortex, the points are divided into three types: core points, boundary points, and outliers. All core points or boundary points connected in density will be clustered into one category.
Figure 8a describes DBSCAN, where the voxels are simplified into rectangular windows. The length in the azimuth direction, the width in the range direction, and the height in the elevation direction are marked as
,
and
, respectively. The minimum number of points is marked as
. Points
and
are density connected to each other since there is a chain of points between them.
Then, denoising is performed. After DBSCAN, the category information is added to the points, and the outliers are marked by a prior label. Meanwhile, some points that are not considered as outliers but do not conform to the terrain trend can be grouped into categories different from that of targets. By setting the removal label, the unwanted points can be removed.
DBSCAN is damaged by intersection. As a result, the points from different elevation periods but connected in density will be clustered into one category, i.e., abnormal category. It is impossible to obtain the correct result by performing the same elevation shift on the abnormal category. When the abnormal category appears in the segmentation result, the second GMM-based clustering will be executed. As shown in
Figure 8b, the distribution model of the points is assumed to be a linear combination of K-single Gaussian models. The clustering algorithm based on the distribution model can describe complex spatial shapes. In fact, the abnormal points belong to different elevation periods corresponding to different terrain. That is to say, the abnormal categories can be divided into categories satisfying different distributions by GMM. In this paper, the 2D position information of the range and the elevation is used as the input feature vector. The Bayesian Information Criterion (BIC) is used to estimate the optimal number of category [
31]. Meanwhile, the Expectation Maximum (EM) algorithm is used to determine the coefficients of the GMM [
32].
Finally, the two-step clustering results will be merged to acquire the segmentation result.
4.2. Reorganization
The purpose of reorganization is to automatically move the points to the correct elevation position. First, the segmentation result is extended in the elevation direction. To elaborate, the segmentation result will be copied on adjacent elevation periods. is the elevation span of the processing slice, which is equal to the rounding up of the ratio of the elevation span to the elevation ambiguity of the TomoSAR system. Elevation extension ensures that all points are moved to the correct elevation period. However, the downside is that all points will also be moved to the error periods, and the categories are independent.
Then, a combination is performed for all the categories obtained from elevation extension. The combination ensures that each basic event contains all categories, but the same category does not repeat. Suppose that the number of categories after segmentation is . The total number of basic events is . Among them, one and only one basic event represents the real point cloud distribution, which is called the optimal basic event in the following.
Finally, the basic events that do not satisfy the boundary constraint and the elevation continuity constraint are eliminated. Performing boundary constraint, the basic events whose all points are within the elevation boundary are retained. These boundary values are obtained by specifying the start category and the end category. Because some interference events also comply with boundary constraint, elevation continuity constraint is further applied. According to the spatial continuity, the real point cloud without terrain occlusion is continuous on the ground-elevation plane. Although the continuity may be corrupted by shadowing, the near-end and the far-end of holes are continuous in the elevation direction. Therefore, the elevation continuity is effective even for the complex terrain with shadowing. Considering the impact of missed detection, the maximum elevation difference of the optimal basic event is the smallest of all basic events.
Here, the advantages of geometric constraints are explained. As mentioned above, the total number of basic events depends on the elevation ambiguity number and the number of segmentation categories. The former is an inherent parameter jointly determined by the system ambiguous elevation and the observation scene elevation span. The latter cannot exceed the lower limit, that is, the optimal number of segmentation categories is equal to the elevation ambiguity number. So, the total number of basic events is greater than one. If geometric constraints are not used, the processor needs to interpret and judge one by one from all the reorganization results. Instead, the geometric constraints given in this paper helps to automatic eliminate the interfering basic events, which significantly improves the extraction efficiency of the real point cloud.
6. Conclusions
Three-dimensional (3D) mountain reconstruction is crucial to topographic surveying and mapping, bridge erection, disaster prevention and mitigation, etc. However, the problem of elevation ambiguity makes the original point cloud geometrically deformed. In-depth analysis of geometric distortion and the principle of layover solution, the cause of the difficulties in solving the elevation ambiguity problem is explained. Furthermore, the law of TomoSAR point cloud is derived. Motivated by the elevation boundary constraint and the elevation continuity constraint of TomoSAR point cloud, an elevation ambiguity resolution method is proposed in this paper. The method mainly includes two steps including segmentation and reorganization. The performance of the proposed method is illustrated by both simulated data and the real airborne array TomoSAR data. The comparison with the traditional methods demonstrates that even in the case of intersection, the proposed method is effective. Based on the real results, the 3D mountain images are further presented. The results show that these images with the proposed method have similar topographic features with the optical image, AW3D30 DSM and 1:10,000 DEM. With DSM as the true value, the average elevation error of the 3D reconstruction result is 6.62 m.
There are several aspects of the proposed method that can be improved in the future. Firstly, the automatic identification of abnormal category needs to be further studied. Secondly, if the abnormal category conforms to multiple distributions with large differences, more categories are needed to separate them. This will increase the total number of basic events and increase the difficulty of the optimal basic event extraction. Future work will focus on these factors, and strive to obtain more robust method for solving the problem of elevation ambiguity. Moreover, the high-precision 3D mountain reconstruction using airborne array TomoSAR will also be considered.