A Spatial Downscaling Methodology for GRACE Total Water Storage Anomalies Using GPM IMERG Precipitation Estimates

Abstract

A downscaling framework for coarse resolution Gravity Recovery and Climate Experiment (GRACE) Total Water Storage Anomaly (TWSA) data is described, exploiting the observations of precipitation from the Global Precipitation Measurement (GPM) mission, using the Integrated Multi-satellite Retrievals for GPM (IMERG). Considering that the major driving force for changes in TWS is precipitation, we tested our hypothesis that coarse resolution, i.e., 1°, GRACE TWSA can be effectively downscaled to 0.1° using GPM IMERG data. The algorithm for the downscaling process comprises the development of a regression equation at the coarse resolution between the GRACE and GPM IMERG data, which is then applied at the finer resolution with a subsequent residual correction procedure. An ensemble of GRACE data from three processing centers, i.e., GFZ, JPL and CSR, was used for the time period from June 2018 until March 2021. To verify our downscaling methodology, we applied it with GRACE data from 2005 to 2015, and we compared it against modeled TWSA from two independent datasets in the Thrace and Thessaly regions in Greece for the same period and found a high performance in all examined metrics. Our research indicates that the downscaled GRACE observations are comparable to the TWSA estimated with hydrological modeling, thus highlighting the potential of GRACE data to contribute to the improvement of hydrological model performance, especially in ungauged basins.

1. Introduction

Hydrological models are essential tools for the reliable nowcasting and forecasting of terrestrial water resources. Acquiring realistic forecasts and sufficiently accurate estimates of the hydrological variables under various future climate and land-use change scenarios requires a rigorous calibration process [1,2], which in turn relies on a proper dataset of hydrological observations, either in situ or from remote sensing. Ground monitoring networks for surface waters (i.e., river discharge monitoring stations, precipitation gauges and lake levels) are present in many parts of the world like North America and Europe and provide precious hydrological information. However, they lack the necessary spatial density in large areas like Africa, South America and Asia, to capture the heterogeneity of hydrological variability [3]. Even less information is available for groundwater resources, especially in modern, i.e., less than 50 years old, groundwater, which is particularly exposed to climate change impacts [4]. Remote sensing has been providing unprecedented hydrological information globally over the last few decades, at spatial and temporal resolutions of practical use [3], which can be assimilated into hydrological models.

The Gravity Recovery and Climate Experiment (GRACE) is a joint mission of the National Aeronautics and Space Administration (NASA) and the Deutsches Zentrum für Luft und Raumfahrt (DLR). GRACE satellites have been detecting changes in the Total Water Storage (TWS) from 2002 until present, with global coverage every 30 days. The initial mission, scheduled for a five-year operation, continued until October 2017, with data release being interrupted at increasing intervals during the last years of operation as a result of the energy-saving operation plan for the degraded power system [5]. Its successor mission, GRACE-Follow On (GRACE-FO), was launched in May 2018 and is still operating successfully at this time. Long-term ice mass changes and sea level rise monitoring are perhaps the most well-known applications of GRACE observations [6,7]. GRACE observations have been increasingly used to monitor TWSA (i.e., changes in the sum of surface water, snow cover, soil moisture and groundwater) in large basins all over the world [8,9] to estimate changes in different water storage components [10,11,12,13]. Meanwhile, the advantages of assimilating GRACE information into hydrological models have also been highlighted in previous works [14,15,16], thus indicating the vast potential of GRACE to contribute to practical applications such as drought and flood monitoring and forecasting [17,18,19], assessment of groundwater sustainability [20] and the allocation of drinking water supplies [8]. GRACE data have been combined with modeling information to estimate groundwater depletion at the global scale [21], whereas a methodology to assimilate GRACE within WaterGAP Global Hydrology Model and improve its performance using an ensemble-based Kalman filter was presented in [22]. Besides the coarse spatial resolution of GRACE observations, which presents a challenge while assimilating GRACE data into hydrological models, many works have shown the potential of GRACE information to improve spatiotemporal characterization of the various hydrological variables like groundwater levels [23], changes in TWS [24] or indices like renewable groundwater stress [12,25] and groundwater abstractions [26].

The main disadvantage of GRACE data is the coarse spatial resolution which limits its applicability to large basins. Therefore, GRACE Level 2 products at a spatial resolution of ~3° are processed to release gridded Level 3 products at grid cell of 0.5° × 0.5° or 1° × 1°. Nevertheless, the higher resolution of Level 3 products do not contain more physical information than the coarse resolution of native GRACE datasets, and downscaling at higher spatial resolution is necessary to acquire high-resolution TWSA estimates that are useful for small scale studies [15,27].

Previous works have shown that assimilating information from auxiliary variables at higher spatial resolution can improve the coarse spatial resolution of remotely sensed products like soil moisture [28,29,30,31,32] or TWS changes, also known as TWS anomalies [15]. Currently, there are two main downscaling approaches, which differ in their nature but also in terms of input data requirements. Physically-based downscaling methods, also known as dynamical downscaling, establish a physical model between the coarse resolution variable to be downscaled and the fine resolution auxiliary variables. Dynamical downscaling relies on a sound physical basis; its implementation is, however, computationally demanding. On the other hand, statistical downscaling seeks a statistical relationship between the coarse and fine-scale variables. The statistical approach is more simple to implement compared to the dynamic downscaling, but the establishment of a statistical relationship requires a large and reliable dataset, and the result depends highly on the choice of auxiliary high-resolution variables [15,28]. An example can be found in the downscaling of soil moisture that has received considerable attention. One of the methods is the use of thermal inertia and vegetation and surface temperature to downscale passive microwave radiometer estimates of soil moisture from AMSR-E (Advanced Microwave Scanning Radiometer) [33], AMSR2 [34] and SMAP (Soil Moisture Active Passive) [35,36,37].

Within the present work, a spatial statistical downscaling approach for GRACE TWS anomalies (TWSA), from the original 1° grid to 0.1°, is presented. The methodology uses the finer resolution, i.e., 0.1°, remotely sensed precipitation from GPM-IMERG, and a pixel-wise regression formula is computed, accounting for the time lags between precipitation and TWSA. While most previous downscaling methods of GRACE have relied on modeled fine-resolution information [15,38], in the present work, we evaluated the downscaling ability of a sole remotely sensed product, i.e., GPM-IMERG, to produce a simple yet reliable downscaling framework for GRACE TWS changes.

2. Materials and Methods

2.1. Study Area Description

The downscaling methodology for GRACE-derived TWSA is demonstrated at the national level in Greece. The country demonstrates a variable climate, with typical Mediterranean parts being the Aegean islands and most of the south continental areas, with hot and dry summers and mean annual precipitation of ~400 mm/year. Western Greece, with an Alpine climate, is distinguished from the rest of the country due to the almost double precipitation that it receives compared to the eastern parts of the country, which reaches >1000 mm/year [12]. The central and northeastern parts of the country are characterized by a temperate climate with much lower precipitation, ranging from 400 mm to 600 mm/year [39]. Agricultural land uses dominate the eastern and northern parts of Greece with a steady increase in areas occupied by irrigated crops [40] that pose serious water stress for many lowland areas in eastern continental Greece, with Thessaly being the most representative case [12]. The hydroclimatic setting described above of adequate natural replenishment in the west and the high water demand in eastern parts of Greece, where natural replenishment is limited, is rather disadvantageous in terms of water resources management [41]. Figure 1 demonstrates the study area and the division of Greece into 14 Water Districts, as a requirement of the EU Water Framework Directive 60/2000, which form the basic hydrological units and river basin management plans are conducted and reported to the EU at regular time intervals. The presented methodology herein will help water authorities highlight areas where persistent negative TWSA are observed, posing a threat to the sustainability of water resources.

2.2. Description of the Dataset

2.2.1. GRACE TWSA Dataset

GRACE and GRACE-FO Level 1B are ranging measurements produced from the raw intersatellite microwave and laser ranging records. There are two fundamentally different GRACE and GRACE-FO Level 2 gravity field solutions, i.e., the spherical harmonics approach and the mass concentration approach, also known as mascon solution, each of which has advantages and limitations [15,42]. Level 3 monthly Total Water Storage changes are computed as surface mass deviations relative to a baseline temporal average (usually 2004–2009) and are known as Total Water Storage Anomalies (TWSA), using either the spherical harmonics or mascon solution. Although those two solutions are different in their nature, their outputs are not much different, and the choice of specific GRACE data is not critical [15]. The GRACE observations were used in the downscaling process as an ensemble mean from the three analysis centers, i.e., Jet Propulsion Laboratory (JPL), Center for Space Research at University of Texas, Austin (CSR) and GeoforschungsZentrum Potsdam (GFZ), with the most recent gravity fields, i.e., release 06 accessed from NASA’s Physical Oceanography Distributed Active Archive Data Center (https://podaac-tools.jpl.nasa.gov/drive/files, accessed date 25 June 2021) [43]. Averaging of the three data centers’ solutions is recommended as it has been found effective in reducing the noise in the gravity field solutions [44,45]. The Level-3 GRACE data used herein are produced using Level-2 spherical harmonics as inputs [46], although the same approach can be applied for the mascon solution products. Error estimates provided along with the GRACE, and GRACE-FO data products were introduced in the analysis to estimate the level of uncertainty in the computed downscaled solution. The time step of GRACE TWSA retrievals is approximately 1 month, although successive records may cover longer or shorter time periods. In the present work, we developed our downscaling approach using only the GRACE-FO time series, starting from June 2018 until March 2021. GRACE-FO has no data gaps, which are frequently encountered during the last years of operation of GRACE, from 2011 until the end of mission, October 2017. GRACE data from 2005 to 2015 was subsequently used to test the methodology comparing the downscaled results to modeled TWSA values for that decade in two regions of Greece.

2.2.2. GPM IMERG Precipitation

The GPM mission offers unprecedented information regarding precipitation that covers the majority of Earth’s surface and is a valuable tool, especially in areas with little or no coverage by ground observations, for climate and weather models, for the management of water resources and for the planning of emergency services aiming to mitigate impacts from natural disasters like storm surges and droughts.

The GPM mission, co-led by NASA and the Japan Aerospace and Exploration Agency (JAXA), comprises a satellite constellation centered on a “Core” satellite equipped with an advanced combined active/passive sensor. The mission integrates precipitation measurements from research and operational microwave sensors from ten partner satellites [47,48], and releases gridded precipitation products at half-hourly, daily or monthly time steps at a spatial resolution of 0.1°. IMERG is the algorithm that combines satellite-derived microwaves with infrared precipitation estimates, along with precipitation gauge data to obtain accurate precipitation estimates with a relatively long time series, suitable for research purposes. There has been remarkable progress in the quantification of spatial variability of precipitation using satellite products. TRMM (Tropical Rainfall Measuring Mission) has been used to compare gage gridded products over India [49] while biases corrected over the United States [50] and GPM (Global Precipitation Measurement Mission) have been used as input for hydrological simulations in river basins in Vietnam [51,52,53], and comparisons with streamflow illustrate that they perform better in simulations.

Daily GPM IMERG final run data of the latest release, i.e., V06, were retrieved from https://gpm1.gesdisc.eosdis.nasa.gov/data/GPM_L3/GPM_3IMERGM.06/ (access date 30 June 2021) [54]. The daily precipitation values were aggregated at the GRACE time steps to acquire a precipitation time series of the same time intervals with those of GRACE for the time period from June 2018 to March 2021. An analogous process was followed for the testing period from 2005 to 2015. To test the performance of the GPM IMERG dataset at the regional level, a comparison exercise was conducted for the two test sites with measured precipitation from meteorological stations operating in the test sites during the 2005 to 2015 period.

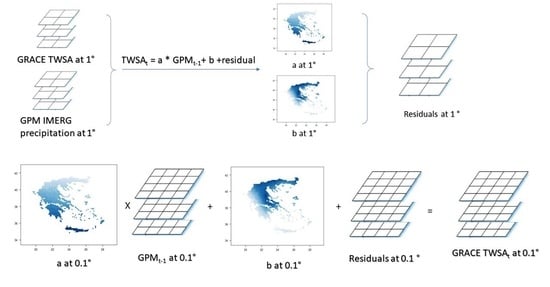
2.3. Development of the Methodology

In the present work, we tested the hypothesis that precipitation datasets at a higher resolution than that of the typical GRACE footprint have the information content needed to downscale GRACE TWSA observations. Precipitation is known to have a strong impact on TWS changes and the individual components of TWS, like soil moisture [27,55]. Precipitation has also been shown to regulate shallow groundwater storage and, to a lower extent, deep groundwater storage [13]. Therefore, we evaluated the ability of a well-known and widely used remotely sensed daily precipitation product, i.e., GPM-IMERG at a spatial resolution of 0.1°, to be used as an auxiliary variable to downscale GRACE TWSA. To account for the time lag and lead between changes in Total Water Storage and precipitation, a cross-correlation at various time lags was performed between TWSA and precipitation.

The methodology follows the schematic diagram shown in Figure 2 and was applied at the national level in Greece, where downscaled time series of GRACE TWSA were constructed at the 0.1° spatial resolution; furthermore, spatial averages were evaluated at the Water District level.

Initially, the GPM IMERG dataset was resampled to 1° to match GRACE TWSA spatial resolution, and their relationship was investigated. Previous works have highlighted the issue of time lags of changes among the various water budget components [15], therefore, a cross-correlation analysis between the changes of GRACE TWSA and GPM precipitation was conducted to determine the time lag(s) that could possibly contribute in the downscaling process. Therefore, the regression equation for each pixel at the coarse spatial resolution will be as follows:

$$T_{1°}^t=a_{1°}+b_{1,1°}{P}_{1°}^t+b_{2,1°}{P}_{1°}^{t-1}+\cdots +b_{n,1°}{P}_{1°}^{t-n}$$

(1)

where $T_{1°}^t$ (m) is the ensemble mean of GRACE TWSA at 1° and time t, and $P_{1°}^t$ (m) is the GPM IMERG precipitation at time lags t resampled at 1°, n denotes the number of time lags between TWSA and precipitation observations, $a_{1°}$ is the intercept of the regression equation and $b_{1,1°}\dots b_{n,1°}$ are the coefficients of the auxiliary variables at a spatial resolution of 1°.

Applying Equation (1), an estimate of GRACE TWSA is obtained and the residuals ${\tilde{T}}_{1°}^t$ were computed by subtracting the original GRACE TWSA data $T_{1°\left(\mathrm{o}\right)}^t$ from the estimated $T_{1°}^t$ from Equation (1):

$${\tilde{T}}_{1°}^t=T_{1°}^t-T_{1°\left(\mathrm{o}\right)}^t$$

(2)

Subsequently, Equation (1) is applied at the finer spatial resolution, i.e., 0.1°, to obtain spatially downscaled GRACE TWSA at improved resolution. The intercept and slope of Equation (1) were resampled to 0.1° using a bilinear interpolation, whereas precipitation observations were used at their native resolution of 0.1°:

$$T_{0.1°}^t=a_{0.1°}+b_{1,0.1°}{P}_{0.1°}^t+b_{2,0.1°}{P}_{0.1°}^{t-1}+\cdots +b_{n,0.1°}{P}_{0.1°}^{t-n}$$

(3)

The final step focuses on correcting the downscaled GRACE TWSA using the residual correction approach. Analogous methodology of residual correction was presented previously while downscaling remotely sensed soil moisture [32] and has been shown to considerably improve the accuracy of the downscaled variable.

Thus, the downscaled TWSA from Equation (3) was then further processed adding the residuals from Equation (2), resampled at 0.1° using a bilinear interpolation:

$${\overline{T}}_{0.1°}^t=T_{0.1°}^t+{\tilde{T}}_{0.1°}^t$$

(4)

where ${\overline{T}}_{0.1°}^t$ is the residually corrected TWSA at 0.1°.

Previous works [20] have shown that the GRACE signal is correlated with precipitation at various lags prior to the GRACE overpass, but also comprises non-climatic factors which are related to human activities, e.g., abstractions for irrigation and domestic water supply. The non-climatic factors cannot be easily incorporated into the model, but the residual correction approach may help to account for those components of the GRACE signal as well.

Evaluation of the downscaled variable was performed at two Water Districts in Greece, i.e., in Thrace (NE Greece) and Thessaly (Central Greece) regions, where modeled results for TWSA from the Soil and Water Assessment Tool (SWAT) [56] from 2005 to 2015 were available from previous research [12]. In the Thrace Water District, the SWAT model refers to two adjacent basins of ~800 km², whereas in Thessaly, the model is applied in a basin of ~11,000 km². TWS from SWAT was computed by summing the individual components of the water budget, i.e., surface runoff, soil water and groundwater recharge at the GRACE time steps. Snow water storage is considered negligible in the examined areas (see provided snow water equivalent from ERA5-Land Monthly Averaged—ECMWF Climate Reanalysis for the two test basins in the Supplementary Material Table S1). The SWAT-based TWSAs were evaluated by subtracting the 2005–2009 TWS mean from each record in the time series to match the GRACE baseline temporal average. In an analogous manner, the GRACE TWSAs were computed for the same baseline period, i.e., 2005 to 2009, following the technique described in [44]. Details of the SWAT model development and application can be found in [12], along with the model parameterization, calibration and verification process. Additionally, the downscaled results were compared to TWSAs estimated from the ERA5-Land Monthly Averaged—ECMWF Climate Reanalysis [57]. ERA5-Land is a global dataset and provides land variables combining model data with observations for several decades at ~11 km spatial resolution. ERA5 Land TWSAs were estimated by adding the individual water components in the two test sites (i.e., surface and subsurface runoff, soil moisture, snow depth, water equivalent) and subtracting the mean TWS for the reference period. Cross-correlation analysis has been conducted at the basin scale, and the GPM time lags with the highest correlation were used in the downscaling computations. The regression equation was then computed for the 2005–2015 period for the two predefined areas, estimating the pixel-wise regression parameters along with the residuals from Equations (1)–(4).

3. Results and Discussion

3.1. Acquired Results at the Country and Water District Levels

The cross-correlation analysis of the GRACE TWSA and GPM IMERG precipitation was conducted at the pixel level, after resampling GRACE TWSA from its native 1° at 0.1°, to match the resolution of GPM IMERG. Results of cross-correlation analysis at various lags and the country averaged correlation coefficients are shown in Figure 3. Thus, it can be seen that the highest correlation of 0.57 between the two variables was observed at a lag of 1 month, implying that it takes approximately 1 month for precipitation to be observed as changes in TWS. The second-highest correlation coefficient of 0.41 was observed at lag 2. Considering the inherent differences of those two datasets, but most importantly the difference in the spatial resolution, the correlation coefficient at lags 1 and 2 constitutes GPM IMERG, a promising auxiliary variable to downscale GRACE TWSA.

Concerning the spatial patterns of correlation, it seems that the southwestern parts of the country demonstrate higher correlation values. The northeastern parts, where most agricultural activities and groundwater abstractions take place, have lower values of correlation of GPM IMERG and GRACE data. Therefore, the pixel-based regression formula from Equation (1) was then arranged as follows:

$$T_{1°}^t=a_{1°}+b_{1,1°}{P}_{1°}^{t-1 }+b_{2,1°}{P}_{1°}^{t-2}$$

(5)

and it was then applied at the 0.1° spatial resolution, by using the GPM IMERG dataset at its native resolution, i.e., 0.1°, and resampling the intercept a, and the precipitation coefficients b₁ and b₂ at the finer resolution using a bilinear interpolation:

$$T_{0.1°}^t=a_{0.1°}+b_{1,0.1°}{P}_{0.1°}^{t-1}+b_{2,0.1°}{P}_{0.1°}^{t-2}$$

(6)

Further, the residuals were computed from Equation (2) and were added to the TWSA from Equation (6), applying Equation (4), to obtain the downscaled and residually corrected TWSA.

A comparison of the downscaling outcome before and after residual correction is demonstrated in Figure 4. The scatterplot on the left of Figure 4 shows the ensemble of GRACE TWSA data against the downscaled outcome before residual correction, indicating that most of the data points are above the y = x line (i.e., 1:1 line, black line on Figure 4) when TWSA is lower than −0.03 and r² is 0.59. The right-hand panel on the same figure demonstrates that after residual correction, the data points are distributed evenly above and below the 1:1 line and r² is 0.87, considerably higher compared to the r² estimated before residual correction, implying improvement with the residual correction applied. Analogous improved results have been found by applying the residual correction approach while downscaling other remotely sensed data products, such as soil moisture [32]. To the best of our knowledge, it is the first time that such an approach has been tested in the downscaling of GRACE TWSA.

Results of the downscaling outcome are provided in Figure 5 and Figure 6. Figure 5 demonstrates the original GRACE-FO time series from June 2018 to March 2021, covering the study area. Figure 6 shows the downscaled outcome of TWSA in Greece. Please note that due to the time lags incorporated in Equations (5) and (6), the downscaled time series has a slightly different time coverage, i.e., from October 2018 to March 2021 (for details on GRACE-FO dates, please refer to GRACE dates in the Supplementary Table S1). The time series of the auxiliary variable used in the present work to downscale GRACE TWSA, i.e., GPM IMERG, is shown in Figure 7. The corresponding downscaled TWSA shown in Figure 6, can be found in the Supplementary material accompanying the present work (GREECE_TWSA.tiff). The spatial pattern of GRACE-FO original data in Figure 5 indicates that the north and eastern parts of the country are mostly affected by negative TWSA, especially during late summer (August) and autumn months. Those parts correspond to areas where most agricultural activities are found; the water demand is high and receives much less precipitation compared to western Greece. This specific spatial pattern is also reflected in the downscaled results shown in Figure 6; however, the impact of low precipitation is also evident from May to December 2020, where most of the country demonstrates negative TWSA in Figure 6, which agrees with the low precipitation patterns evidenced in Figure 7.

Results of the downscaling methodology are presented as Water District means for the whole country. The WD means for the coarse resolution GRACE TWSAs were evaluated after resampling the coarse resolution dataset to 0.1° by a bilinear interpolation and then extracting the regional mean TWSA from the new resampled GRACE TWSAs. Thus, Figure 8 presents the GRACE-FO TWSA before and after downscaling along with GPM precipitation, averaged over each one of the 14 Water Districts of Greece.

The associated uncertainty related to each Water District can be found in the Supplementary Material (Table S1) acquired from the gridded fields of leakage and GRACE measurement errors [44], where a mean error of 15.9 mm at the country scale is estimated. GR13 and GR14 Water District refer to Crete and Aegean Islands, respectively, and their results in terms of GRACE TWSA error are reported only slightly higher compared to those of the continental part of the country. However, since the land areas occupied by those two regions are below the typical GRACE footprint and are surrounded by sea, the downscaling outcome should be evaluated very cautiously, as it might have been impacted by sea mass changes. Comparing the graphs of Figure 8, it is evident that at the regional scale, there is consistency between the original and downscaled TWSA, i.e., the downscaled result preserves the major GRACE patterns, whereas the time lag of 2 months slightly shifted the downscaled TWSA. The Water Districts in the eastern and northern parts of the country (GR6 to GR12) received much lower precipitation and demonstrated mostly negative TWSA with higher temporal variability. On the contrary, the western Water Districts with much higher precipitation demonstrated mostly positive TWSA and much lower temporal variability compared to those in northeastern Greece. Regarding the time lags used in the downscaling of TWSA, Figure 8 reveals that at the Water District level, the downscaled product offers a more consistent time variation of TWSA with that of precipitation. In some Water Districts, there might be additional time lags that could offer additional information to the downscaling process. This is because the downscaling process has been conducted at the country level, thus suppressing local differences in the correlation of precipitation lags with TWSA. Thus, in the next section, a demonstration of the downscaling methodology is presented for two individual Water Districts.

3.2. Comparison of Downscaled Outcome with Modeled Results in Thrace and Thessaly

The methodology outlined in the previous sections has been applied in the Thrace and Thessaly Water Districts. Initially, the GPM dataset for the time period 2005–2015 was compared to measured precipitation from 4 and 6 meteorological stations operating in Thrace and Thessaly, respectively. Spatial averages for the whole study basins were estimated for each time step from point measurements using Thiessen polygons. Scatterplots of the observed (ground measured) and GPM-IMERG monthly precipitation are shown in Figure 9 for the two examined basins, indicating a satisfactory agreement of the two datasets at the monthly time step. This finding is in agreement with other evaluation studies of the GPM IMERG dataset conducted previously in the study area [58] and concluded on the reliable performance of this specific dataset.

To determine the time lags that could possibly contribute to the downscaling, the cross-correlation analysis presented in Section 3.1 was applied at the two study areas from 2005 to 2015 and comprised time lags up to 12 months, in order to estimate any possible contribution of precipitation up to one year before. Analogous time lags could not be covered with the GRACE-FO period until today, because it was too short to allow estimation of such time lags. Results of the cross-correlation analysis at the two test basins are shown in Figure 10 and indicate that in the Thrace area, a time lag of 1 month is high enough to support its role in the regression process. In the Thessaly basin, both time lags of 1 and 2 months demonstrate high enough values for their use in the downscaling process. The verification outcome of the downscaling approach is shown in Figure 11 and Figure 12. In Figure 11, the computed pixel-wise intercept and slope for the Thessaly and Thrace regions using the time series from 2005 to 2015 are presented. A comparison of the modeled and downscaled TWSA is demonstrated in Figure 12. Therein, the modeled TWSA during 2005–2015 is examined against the ensemble of GRACE TWSA and downscaled GRACE TWSA (the associated datasets are provided in the Supplementary material Table S1).

When it comes to the basin scale, it can be seen that the results are improved, indicating that the downscaled GRACE TWSA captures both the regional and basin-scale variability of TWS. Therefore, r² is considerably improved between modeled and downscaled TWSA, reaching a value of 0.85 and 0.94 in Thrace and Thessaly, respectively, whereas the r² between the original GRACE TWSA and the modeled TWSA is 0.42 and 0.49 for the predefined areas. An improvement is also observed comparing r² for the ERA5 Land TWSA and the downscaled TWSAs. In that case, the r² for Thrace is 0.94 and for Thessaly 0.92, while r² for ERA5 Land TWSAs and GRACE TWSA was found to be 0.74 and 0.79 for Thrace and Thessaly, respectively. Two other performance metrics were evaluated to measure the performance of the downscaling algorithm. In that way, the Mean Absolute Error (MAE), which measures the distance between observed ($O_i$) and predicted (P_i) values of a dataset of size N was computed [23]:

$$MAE=\frac{1}{N}{\displaystyle \sum }_{i=1}^N|P_i-O_i|$$

(7)

as well as the Scaled Root Mean Squared Error ($R^{*}$), where ${\sigma }_o$ is the standard deviation of observed values:

$$R^{*}=\frac{RMSE}{{\sigma }_o}=\frac{\sqrt{\frac{1}{N}{\sum }_{i=1}^N{\left(P_i-O_i\right)}^2}}{{\sigma }_o}$$

(8)

The downscaled TWSA compared to SWAT-modeled TWSA demonstrated MAE 24.0 mm and 16.5 mm for Thrace and Thessaly basins, whereas, for the original GRACE time series, the MAE ranges from 51.5 mm (Thrace) to 47.0 mm (Thessaly). Regarding the comparison with the ERA5 TWSAs, MAE decreased from 30.6 to 13.4 mm in Thrace and from 28.6 to 16.9 in Thessaly. Analogous improvement was observed while analyzing the $R^{*}$ index. Therefore, compared to SWAT TWSAs, $R^{*}$ decreased from 0.83 to 0.41 in the Thrace area for the downscaled TWSA, and from 0.78 to 0.28 in Thessaly. Compared to ERA5 TWSAs, the $R^{*}$ index was also improved in the downscaled product, from 0.59 to 0.25 in Thrace and from 0.48 to 0.30 in Thessaly. In all examined metrics, the outcome indicates that there is a considerable improvement in the downscaled TWSA in both areas. Observing both graphs in Figure 12, it is evident that the downscaled TWSAs better represent the timing of TWSA, as a result of the incorporation of the auxiliary variable, i.e., GPM IMERG, at the detected lags, i.e., lag 1 for Thrace and lag 1 and 2 for Thessaly. The above-presented results highlight the advantages of the analysis at the basin scale, where time lags are customized based on the cross-correlation analysis for each basin separately. The close performance of the downscaled and modeled TWSA indicate that the downscaled product can possibly contribute to the constraining of hydrological models, which has been reported to offer a substantial improvement to model results [16].

3.3. Limitations and Future Challenges

The methodology presented herein for downscaling GRACE TWSA is a simple but reliable approach to acquire TWSA estimates at considerably higher spatial resolution than the typical GRACE footprint. It can be applied using times series of GRACE/GRACE-FO TWSA and GPM IMERG, where pixel-wise parameters of the regression equation are evaluated, considering the time lags between TWSA and precipitation. An obvious limitation is the inherited uncertainty of the remotely sensed information and the uncertainty introduced in the various computational steps, e.g., the resampling process. Previous works have relied mostly on a combination of modeled and remote sensing variables as auxiliary downscaling variables [15,59,60]. In the present work, the downscaling ability of a single remotely sensed dataset, i.e., GPM IMERG was evaluated using a regression formula with a residual correction algorithm, and the results are satisfactory. Other computational approaches, like machine learning, are also challenging alternatives, which may result in improved outcomes. Future works may focus on the use of corrected GPM IMERG datasets with ground measurements to acquire a better representation of the spatial variability of precipitation. Although GPM IMERG is considered as a global state-of-the-art precipitation dataset that is constantly improved, it has an inherent source of uncertainty, like all remotely sensed products. While previous works have highlighted the value of GPM IMERG products in hydrological research, there is an uncertainty in acquired estimates, and correction using ground measurements improves the reliability of the precipitation estimates [47], and this, in turn, can have a better representation of water resources variability and consequently in the downscaling outcome. Other auxiliary variables, known to influence the TWS, like topography in the form of the Digital Elevation Model (DEM), can also be incorporated easily in the downscaling process; however, topography implicitly impacts the GPM IMERG algorithm by the numerous gauge stations used in the validation efforts of the GPM products [61]. Nevertheless, one should keep in mind that incorporating many different auxiliary variables in the downscaling process may result in a complex process and may introduce additional sources of uncertainty. In the present work, the GRACE-FO data period was used to develop our methodology, as the pre-2018 period is influenced by temporal data gaps in the GRACE datasets. However, it should be noted that the presented approach can also be applied as a possible gap-filling method for GRACE missing months, especially during 2015–2018, where data gaps are frequent. A future challenge is to evaluate the potential for improvement of GRACE data temporal resolution using the daily GPM IMERG product.

4. Conclusions

Hydrological models have expanded from their traditional role in water resource management and are becoming increasingly useful tools for nowcasting and forecasting natural disasters such as droughts and floods and for the planning of measures against impacts of climate change, wildfires and landslides. One of the main obstacles while simulating hydrological processes is the lack of sufficient ground observations to calibrate and validate the models. With the increasing information offered from remote sensing observations, these models can be improved, provided that remote sensing data are consistent with the spatial and temporal scales required for these hydrological predictions. The present work evaluates GRACE TWSA at an enhanced spatial representation, i.e., from 1° to 0.1°, developing a simple yet reliable approach and a suitable output to be used as a constraining parameter in hydrological models. The methodology is based on a regression formula with a residual correction algorithm. A single hydrological dataset, i.e., GPM IMERG providing daily precipitation retrievals at 0.1°, was evaluated for its downscaling ability of the GRACE TWSA, also considering the time lags between the changes in Total Water Storage and precipitation. The residual correction improved the consistency of the original and downscaled TWSA. The GRACE-FO period was used to develop the downscaling approach, and the methodology was tested computing the pixel-wise regression formula in two Water Districts of Greece (Thrace and Thessaly) and was found to improve the TWSA estimates compared to modeled TWSA from two independent datasets, for the period 2005 to 2015, in all examined metrics. Since GRACE TWSA has been mainly used for large basins, the simple downscaling technique presented in this work may prove to be useful for the applicability of GRACE data at finer scales.