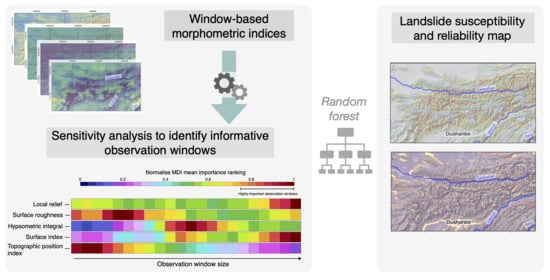
Window-Based Morphometric Indices as Predictive Variables for Landslide Susceptibility Models
Abstract
:1. Introduction
2. Study Area
Landslides
3. Methodology
- compilation and/or construction of several predictive variables from the information of the study area;
- set up of a random forest algorithm for the predictive variables and landslide catalogue characteristics;
- sensitivity analysis to identify informative observation windows; and,
- evaluation of results and reliability assessment.
3.1. Predictive Variables
3.1.1. Available Thematic Information
3.1.2. DEM-Based Predictive Variables
Hydrological Indices
Simple Morphometric Indices
Window-Based Morphometric Indices
3.2. Set Up of the Random Forest Algorithm for Landslide Susceptibility Assessment
3.3. Sensitivity Analysis to Identify Highly Informative Observation Windows
3.4. Evaluation Metrics
4. Results
4.1. Predictive Variable
4.2. Sensitivity Analysis to Identify Informative Observation Windows
4.2.1. Base Models
4.2.2. Fixed Observation Window
4.2.3. Independent Observation Window
4.3. Landslide Susceptibility Map and Reliability
5. Discussion
5.1. General Observations
5.2. Contribution of Predicting Variables to the Landslide Susceptibility Models
5.3. Evaluation Metrics
5.4. Portability and Reproducibility
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DEM | Digital elevation model |
| MDI | Mean decrease impurity |
| ROC | Receiver operator curve |
| AUC-ROC | Area under the receiver operator curve |
| PRC | Precision-recall curve |
| AUC-PRC | Area under the precision-recall curve |
| TWI | Topographic wetness index |
| NDVI | Normalized difference vegetation index |
Appendix A. Datasets







Appendix B. Landslide Density

References
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Fabbri, A.G.; Chung, C.J.F.; Cendrero, A.; Remondo, J. Is prediction of future landslides possible with a GIS? Nat. Hazards 2003, 30, 487–503. [Google Scholar] [CrossRef]
- Marchesini, I.; Ardizzone, F.; Alvioli, M.; Rossi, M.; Guzzetti, F. Non-susceptible landslide areas in Italy and in the Mediterranean region. Nat. Hazards Earth Syst. Sci. 2014, 14, 2215–2231. [Google Scholar] [CrossRef] [Green Version]
- Burrough, P.A.; McDonnell, R.; McDonnell, R.A.; Lloyd, C.D. Principles of Geographical Information Systems; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Shahzad, F.; Gloaguen, R. TecDEM: A MATLAB based toolbox for tectonic geomorphology, Part 2: Surface dynamics and basin analysis. Comput. Geosci. 2011, 37, 261–271. [Google Scholar] [CrossRef]
- Andreani, L.; Stanek, K.; Gloaguen, R.; Krentz, O.; Domínguez-González, L. DEM-based analysis of interactions between tectonics and landscapes in the Ore Mountains and Eger Rift (East Germany and NW Czech Republic). Remote Sens. 2014, 6, 7971–8001. [Google Scholar] [CrossRef] [Green Version]
- Domínguez-González, L.; Andreani, L.; Stanek, K.; Gloaguen, R. Geomorpho-tectonic evolution of the Jamaican restraining bend. Geomorphology 2015, 228, 320–334. [Google Scholar] [CrossRef]
- Andreani, L.; Gloaguen, R. Geomorphic analysis of transient landscapes in the Sierra Madre de Chiapas and Maya Mountains (northern Central America): Implications for the North American–Caribbean–Cocos plate boundary. Earth Surf. Dyn. 2016, 4, 71–102. [Google Scholar] [CrossRef] [Green Version]
- Othman, A.A.; Gloaguen, R.; Andreani, L.; Rahnama, M. Improving landslide susceptibility mapping using morphometric features in the Mawat area, Kurdistan Region, NE Iraq: Comparison of different statistical models. Geomorphology 2018, 319, 147–160. [Google Scholar] [CrossRef]
- Conforti, M.; Ietto, F. Influence of tectonics and morphometric features on the landslide distribution: A case study from the Mesima Basin (Calabria, South Italy). J. Earth Sci. 2020, 31, 393–409. [Google Scholar] [CrossRef]
- Aizen, E.M.; Aizen, V.B.; Melack, J.M.; Nakamura, T.; Ohta, T. Precipitation and atmospheric circulation patterns at mid-latitudes of Asia. Int. J. Climatol. J. R. Meteorol. Soc. 2001, 21, 535–556. [Google Scholar] [CrossRef]
- Pohl, E.; Gloaguen, R.; Seiler, R. Remote sensing-based assessment of the variability of winter and summer precipitation in the Pamirs and their effects on hydrology and hazards using harmonic time series analysis. Remote Sens. 2015, 7, 9727–9752. [Google Scholar] [CrossRef] [Green Version]
- Havenith, H.B.; Strom, A.; Torgoev, I.; Torgoev, A.; Lamair, L.; Ischuk, A.; Abdrakhmatov, K. Tien Shan geohazards database: Earthquakes and landslides. Geomorphology 2015, 249, 16–31. [Google Scholar] [CrossRef]
- Brookfield, M. Geological development and Phanerozoic crustal accretion in the western segment of the southern Tien Shan (Kyrgyzstan, Uzbekistan and Tajikistan). Tectonophysics 2000, 328, 1–14. [Google Scholar] [CrossRef]
- Worthington, J.R.; Kapp, P.; Minaev, V.; Chapman, J.B.; Mazdab, F.K.; Ducea, M.N.; Oimahmadov, I.; Gadoev, M. Birth, life, and demise of the Andean–syn-collisional Gissar arc: Late Paleozoic tectono-magmatic-metamorphic evolution of the southwestern Tian Shan, Tajikistan. Tectonics 2017, 36, 1861–1912. [Google Scholar] [CrossRef]
- Käßner, A.; Ratschbacher, L.; Jonckheere, R.; Enkelmann, E.; Khan, J.; Sonntag, B.L.; Gloaguen, R.; Gadoev, M.; Oimahmadov, I. Cenozoic intracontinental deformation and exhumation at the northwestern tip of the India-Asia collision—southwestern Tian Shan, Tajikistan, and Kyrgyzstan. Tectonics 2016, 35, 2171–2194. [Google Scholar] [CrossRef]
- Abdulhameed, S.; Ratschbacher, L.; Jonckheere, R.; Ga˛gała, Ł.; Enkelmann, E.; Käßner, A.; Kars, M.A.; Szulc, A.; Kufner, S.K.; Schurr, B.; et al. Tajik basin and southwestern Tian Shan, northwestern India-Asia collision zone: 2. Timing of basin inversion, Tian Shan mountain building, and relation to Pamir-plateau advance and deep India-Asia indentation. Tectonics 2020, 39, e2019TC005873. [Google Scholar] [CrossRef]
- Arrowsmith, J.R.; Strecker, M.R. Seismotectonic range-front segmentation and mountain-belt growth in the Pamir-Alai region, Kyrgyzstan (India-Eurasia collision zone). Geol. Soc. Am. Bull. 1999, 111, 1665–1683. [Google Scholar] [CrossRef]
- Evans, S.G.; Roberts, N.J.; Ischuk, A.; Delaney, K.B.; Morozova, G.S.; Tutubalina, O. Landslides triggered by the 1949 Khait earthquake, Tajikistan, and associated loss of life. Eng. Geol. 2009, 109, 195–212. [Google Scholar] [CrossRef]
- Dodonov, A.E.; Baiguzina, L. Loess stratigraphy of Central Asia: Palaeoclimatic and palaeoenvironmental aspects. Quat. Sci. Rev. 1995, 14, 707–720. [Google Scholar] [CrossRef]
- Zech, R.; Röhringer, I.; Sosin, P.; Kabgov, H.; Merchel, S.; Akhmadaliev, S.; Zech, W. Late Pleistocene glaciations in the Gissar Range, Tajikistan, based on 10Be surface exposure dating. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2013, 369, 253–261. [Google Scholar] [CrossRef]
- Vinninchenko, S. Landslide blockages in Tadjikistan mountains (Gissar-Alai & Pamirs): Their origin and development. In Security of Natural and Artificial Rockslide Dams: Extended Abstract Volume; NATO Advanced Res. Workshop: Bishkek, Kyrgyzstan, 2004; pp. 189–194. [Google Scholar]
- Krestnikov, V.; Nersesov, I.; Stange, D. The relationship between the deep structure and Quaternary tectonics of the Pamir and Tien-Shan. Tectonophysics 1984, 104, 67–83. [Google Scholar] [CrossRef]
- Ishiara, K.; Okusa, S.; Oyagi, N.; Ischuk, A. Liquefaction-induced flow slide in the collapsible loess deposit in Soviet Tajik. Soils Found. 1990, 30, 73–89. [Google Scholar] [CrossRef] [Green Version]
- Strom, A. Landslide dams in Central Asia region. J. Jpn. Landslide Soc. 2010, 47, 309–324. [Google Scholar] [CrossRef] [Green Version]
- Saponaro, A.; Pilz, M.; Wieland, M.; Bindi, D.; Moldobekov, B.; Parolai, S. Landslide susceptibility analysis in data-scarce regions: The case of Kyrgyzstan. Bull. Eng. Geol. Environ. 2014, 74. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.H.; Sameen, M.I.; Pradhan, B.; Park, H.J. Modeling landslide susceptibility in data-scarce environments using optimized data mining and statistical methods. Geomorphology 2018, 303, 284–298. [Google Scholar] [CrossRef]
- Carrara, A.; Cardinali, M.; Detti, R.; Guzzetti, F.; Pasqui, V.; Reichenbach, P. GIS techniques and statistical models in evaluating landslide hazard. Earth Surf. Process. Landforms 1991, 16, 427–445. [Google Scholar] [CrossRef]
- Lee, S.; Ryu, J.H.; Kim, I.S. Landslide susceptibility analysis and its verification using likelihood ratio, logistic regression, and artificial neural network models: Case study of Youngin, Korea. Landslides 2007, 4, 327–338. [Google Scholar] [CrossRef]
- Yilmaz, I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: A case study from Kat landslides (Tokat—Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Dai, F.; Saraf, A.K. Comparison of different models for susceptibility mapping of earthquake triggered landslides related with the 2008 Wenchuan earthquake in China. Comput. Geosci. 2012, 46, 317–329. [Google Scholar] [CrossRef]
- Ozdemir, A.; Altural, T. A comparative study of frequency ratio, weights of evidence and logistic regression methods for landslide susceptibility mapping: Sultan Mountains, SW Turkey. J. Asian Earth Sci. 2013, 64, 180–197. [Google Scholar] [CrossRef]
- Catani, F.; Lagomarsino, D.; Segoni, S.; Tofani, V. Landslide susceptibility estimation by random forests technique: Sensitivity and scaling issues. Nat. Hazards Earth Syst. Sci. 2013, 13, 2815. [Google Scholar] [CrossRef] [Green Version]
- Federal State Budgetary Institution A.P. Karpinsky Russian Geological Research Institute (FGUP VSEGEI). Cartographic Resources on Regional Geology. 2018. Available online: http://webmapget.vsegei.ru/index.html (accessed on 16 December 2020).
- Mohadjer, S.; Ehlers, T.A.; Bendick, R.; Stübner, K.; Strube, T. A Quaternary fault database for central Asia. Nat. Hazards Earth Syst. Sci. 2016, 16, 529. [Google Scholar] [CrossRef] [Green Version]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Climatologies at high resolution for the Earth’s land surface areas. Sci. Data 2017, 4, 170122. [Google Scholar] [CrossRef] [Green Version]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Segoni, S.; Pappafico, G.; Luti, T.; Catani, F. Landslide susceptibility assessment in complex geological settings: Sensitivity to geological information and insights on its parameterization. Landslides 2020, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Schuster, R.L.; Wieczorek, G.F. Landslide triggers and types. In Proceedings of the First European Conference on Landslides, Prague, Czech Republic, 24–26 June 2002; pp. 59–78. [Google Scholar]
- Zeimetz, F.; Schaefli, B.; Artigue, G.; Hernández, J.G.; Schleiss, A.J. Relevance of the correlation between precipitation and the 0 °C. isothermal altitude for extreme flood estimation. J. Hydrol. 2017, 551, 177–187. [Google Scholar] [CrossRef]
- Kriegler, F. Preprocessing transformations and their effects on multispectral recognition. In Proceedings of the Sixth International Symposium on Remote Sensing of the Environment, University of Michigan, Ann Arbor, MI, USA, 2–6 October 1969; pp. 97–131. [Google Scholar]
- Lu, N.; Godt, J. Infinite slope stability under steady unsaturated seepage conditions. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vision Graph. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Fairfield, J.; Leymarie, P. Drainage networks from grid digital elevation models. Water Resour. Res. 1991, 27, 709–717. [Google Scholar] [CrossRef]
- Jones, R. Algorithms for using a DEM for mapping catchment areas of stream sediment samples. Comput. Geosci. 2002, 28, 1051–1060. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Sørensen, R.; Seibert, J. Effects of DEM resolution on the calculation of topographical indices: TWI and its components. J. Hydrol. 2007, 347, 79–89. [Google Scholar] [CrossRef]
- Rennó, C.D.; Nobre, A.D.; Cuartas, L.A.; Soares, J.V.; Hodnett, M.G.; Tomasella, J. HAND, a new terrain descriptor using SRTM-DEM: Mapping terra-firme rainforest environments in Amazonia. Remote Sens. Environ. 2008, 112, 3469–3481. [Google Scholar] [CrossRef]
- Taylor, D.W. Fundamentals of Soil Mechanics; John Wiley & Sons, Inc.: New York, NY, USA, 1948; Volume 66. [Google Scholar]
- Budimir, M.; Atkinson, P.; Lewis, H. A systematic review of landslide probability mapping using logistic regression. Landslides 2015, 12, 419–436. [Google Scholar] [CrossRef] [Green Version]
- Ahnert, F. Local relief and the height limits of mountain ranges. Am. J. Sci. 1984, 284, 1035–1055. [Google Scholar] [CrossRef]
- Weiss, A. Topographic position and landforms analysis. In Poster Presentation; ESRI User Conference: San Diego, CA, USA, 2001; Volume 200. [Google Scholar]
- De Reu, J.; Bourgeois, J.; Bats, M.; Zwertvaegher, A.; Gelorini, V.; De Smedt, P.; Chu, W.; Antrop, M.; De Maeyer, P.; Finke, P.; et al. Application of the topographic position index to heterogeneous landscapes. Geomorphology 2013, 186, 39–49. [Google Scholar] [CrossRef]
- Trentin, R.; de Souza Robaina, L.E. Study of the landforms of the Obicuí river basin with use of topographic position index. Rev. Bras. Geomorfol. 2018, 19. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.W. Roughness in the Earth Sciences. Earth Sci. Rev. 2014, 136, 202–225. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale analysis of topographic surface roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote. Sens. 2010, 49, 1200–1213. [Google Scholar] [CrossRef] [Green Version]
- Hobson, R.D. Surface roughness in topography: Quantitative approach. In Spatial Analysis in Geomorphology; Chorley, R.J., Ed.; Methuer: London, UK, 1972; pp. 225–245. [Google Scholar]
- Grohmann, C.H. Morphometric analysis in Geographic Information Systems: Applications of free software GRASS and R. Comput. Geosci. 2004, 30, 1055–1067. [Google Scholar] [CrossRef] [Green Version]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Surface roughness of topography: A multi-scale analysis of landform elements in Midland Valley, Scotland. Proceedings of Geomorphometry 2009, Zurich, Switzerland, 31 August–2 September 2009; pp. 140–148. [Google Scholar]
- Strahler, A.N. Hypsometric (area-altitude) analysis of erosional topography. Geol. Soc. Am. Bull. 1952, 63, 1117–1142. [Google Scholar] [CrossRef]
- Schumm, S.A. Evolution of drainage systems and slopes in badlands at Perth Amboy, New Jersey. Geol. Soc. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Pike, R.J.; Wilson, S.E. Elevation-relief ratio, hypsometric integral, and geomorphic area-altitude analysis. Geol. Soc. Am. Bull. 1971, 82, 1079–1084. [Google Scholar] [CrossRef]
- Goetz, J.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in Lianhua County (China): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef] [Green Version]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Chapman and Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Havenith, H.B.; Torgoev, A.; Schlögel, R.; Braun, A.; Torgoev, I.; Ischuk, A. Tien Shan geohazards database: Landslide susceptibility analysis. Geomorphology 2015, 249, 32–43. [Google Scholar] [CrossRef]
- Chang, K.T.; Merghadi, A.; Yunus, A.P.; Pham, B.T.; Dou, J. Evaluating scale effects of topographic variables in landslide susceptibility models using GIS-based machine learning techniques. Sci. Rep. 2019, 9, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wang, Y.; Basu, S.; Kumbier, K.; Yu, B. A debiased MDI feature importance measure for random forests. Adv. Neural Inf. Process. Syst. 2019, 32, 8049–8059. [Google Scholar]
- Hapfelmeier, A.; Hothorn, T.; Ulm, K.; Strobl, C. A new variable importance measure for random forests with missing data. Stat. Comput. 2014, 24, 21–34. [Google Scholar] [CrossRef] [Green Version]
- Nicodemus, K.K. Letter to the editor: On the stability and ranking of predictors from random forest variable importance measures. Briefings Bioinform. 2011, 12, 369–373. [Google Scholar] [CrossRef] [Green Version]
- Saponaro, A.; Pilz, M.; Bindi, D.; Parolai, S. The contribution of EMCA to landslide susceptibility mapping in Central Asia. Ann. Geophys. 2015, 58. [Google Scholar] [CrossRef]
- Kufner, S.K.; Schurr, B.; Ratschbacher, L.; Murodkulov, S.; Abdulhameed, S.; Ischuk, A.; Metzger, S.; Kakar, N. Seismotectonics of the Tajik basin and surrounding mountain ranges. Tectonics 2018, 37, 2404–2424. [Google Scholar] [CrossRef] [Green Version]
- Zimmermann, R.; Brandmeier, M.; Andreani, L.; Mhopjeni, K.; Gloaguen, R. Remote sensing exploration of Nb-Ta-LREE-enriched carbonatite (Epembe/Namibia). Remote Sens. 2016, 8, 620. [Google Scholar] [CrossRef] [Green Version]
- Süzen, M.L.; Kaya, B.Ş. Evaluation of environmental parameters in logistic regression models for landslide susceptibility mapping. Int. J. Digit. Earth 2012, 5, 338–355. [Google Scholar] [CrossRef]
- Erokhin, S.A.; Zaginaev, V.V.; Meleshko, A.A.; Ruiz-Villanueva, V.; Petrakov, D.A.; Chernomorets, S.S.; Viskhadzhieva, K.S.; Tutubalina, O.V.; Stoffel, M. Debris flows triggered from non-stationary glacier lake outbursts: The case of the Teztor Lake complex (Northern Tian Shan, Kyrgyzstan). Landslides 2018, 15, 83–98. [Google Scholar] [CrossRef]
- Pohl, E.; Gloaguen, R.; Andermann, C.; Knoche, M. Glacier melt buffers river runoff in the Pamir Mountains. Water Resour. Res. 2017, 53, 2467–2489. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Vakhshoori, V.; Zare, M. Is the ROC curve a reliable tool to compare the validity of landslide susceptibility maps? Geomat. Nat. Hazards Risk 2018, 9, 249–266. [Google Scholar] [CrossRef] [Green Version]








| Hyperparameter | Definition |
|---|---|
| max_features | Number of features considered for splitting a node. |
| min_sample_split | Minimum number of observations in any given node in order to split the node. |
| min_sample_leaf | Minimum number of samples that should be present in the leaf node after splitting a node. |
| Thematic Group | Predictive Variable | Significance |
|---|---|---|
| Geology | Geology | Rock type association |
| Distance to fault | Effects of seismicity and fragility on surface materials | |
| Climatic | Mean annual precipitation | Soil saturation and rainfall trigger |
| Isothermality | Seasonal temperature influence on rock fragility and snow melting | |
| Landcover | Normalized Difference vegetation index | Slope instabilities in relation to presence or absence of vegetation |
| Hydrology | Elevation above channel | Influence of gradient and potential energy |
| Distance to channel | Influence of river erosion and deposition | |
| Topographic wetness index | Potential saturation | |
| Geomorphology | Slope | Potential energy to mobilize material |
| Aspect | Effects of sun/wind exposition and favorable surfaces for sliding | |
| Local relief | River incision | |
| Topographic position index | Separation of ridges, valley bottoms, and flats | |
| Surface roughness | Erosion | |
| Hypsometric integral | Characterization of degree of landscape erosion and geomorphological evolution | |
| Surface Index | Discrimination between erosional and steady-state landscapes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbosa, N.; Andreani, L.; Gloaguen, R.; Ratschbacher, L. Window-Based Morphometric Indices as Predictive Variables for Landslide Susceptibility Models. Remote Sens. 2021, 13, 451. https://doi.org/10.3390/rs13030451
Barbosa N, Andreani L, Gloaguen R, Ratschbacher L. Window-Based Morphometric Indices as Predictive Variables for Landslide Susceptibility Models. Remote Sensing. 2021; 13(3):451. https://doi.org/10.3390/rs13030451
Chicago/Turabian StyleBarbosa, Natalie, Louis Andreani, Richard Gloaguen, and Lothar Ratschbacher. 2021. "Window-Based Morphometric Indices as Predictive Variables for Landslide Susceptibility Models" Remote Sensing 13, no. 3: 451. https://doi.org/10.3390/rs13030451
APA StyleBarbosa, N., Andreani, L., Gloaguen, R., & Ratschbacher, L. (2021). Window-Based Morphometric Indices as Predictive Variables for Landslide Susceptibility Models. Remote Sensing, 13(3), 451. https://doi.org/10.3390/rs13030451