Joint Hapke Model and Spatial Adaptive Sparse Representation with Iterative Background Purification for Martian Serpentine Detection
Abstract
:1. Introduction
- A joint Hapke model and spatially adaptive sparse representation approach was proposed for subpixel mineral detection. We address the nonlinear issue by introducing the Hapke model, which significantly boosts the detection performance. Furthermore, an iterative background purification strategy is proposed to alleviate the target interference issue, which can be easily implanted into other sparse representation detection algorithms;
- We used a well-designed mineral mixture HSI to evaluate the detection capabilities of our method. The MGS-1 and serpentine were mixed by six different mass fractions to assess the detection performance of the proposed algorithm. This dataset includes detailed groundtruth information, which can serve as a benchmark dataset for martian mineral detection;
- A systematic comparison of several representative detection algorithms was conducted on the laboratory HSI. The detection limit of serpentine abundance by the proposed method was derived. Finally, the proposed method was applied to CRISM images. This study provides a critical link between laboratory measurement and orbital observation.
2. Related Work
2.1. Martian Mineral Mapping Methods
2.2. Sparse Representation for Target Detection
3. Datasets and Methodology
3.1. Datasets
3.1.1. Laboratory Data
3.1.2. Orbital Data
3.2. Methodology
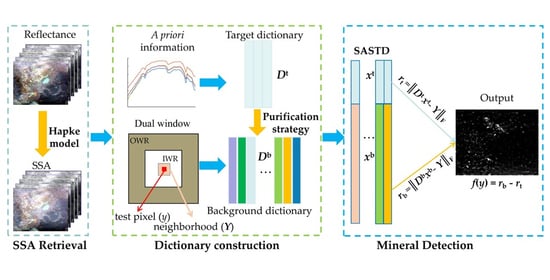
- Single-scattering albedo retrieval. The multiple scattering among mineral particles introduces nonlinearities in reflectance. The SSA is linearly additive in visible and near-infrared wavelengths [27]. The purpose of this step is to convert the reflectance to SSA. Consequently, the linear target detection method can be implemented on SSA data;
- Background and target dictionaries construction. The target dictionary Dt is constructed using a priori knowledge of target spectra, while the background dictionary Db is generated locally through a dual window. However, target pixels may fall into Db due to improper window size settings relative to mineral distribution size or the sliding window process. We propose an iterative background purification method to remove the potential target pixels in Db.
- Spectral reconstruction and target detection. A spatially adaptive sparse representation for target detection (SASTD) is adopted in this work, which incorporates spatial information into target detection. The final detection is in favor of the class that has the lowest reconstruction error.
3.2.1. Single-Scattering Albedo Retrieval
3.2.2. Iterative Background Dictionary Purification
3.2.3. Spectral Reconstruction and Target Detection
3.3. Experimental Settings and Evaluation Metrics
4. Experimental Results
4.1. Experiments with Laboratory Data
4.1.1. Detection Performance
4.1.2. Parameter Analysis
4.2. Application on CRISM Data
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviation | Description |
|---|---|
| AUC | Area Under ROC Curve |
| CAT | CRISM Analysis Toolkit |
| CEM | Constrained Energy Minimization |
| CRISM | Compact Reconnaissance Imaging Spectrometer for Mars |
| hCEM | Hierarchical Constrained Energy Minimization |
| HSI | Hyperspectral Image |
| IBP | Iterative Background Dictionary Purification |
| IWR | Inner Window Region |
| MF | Matched Filter |
| MGS-1 | Mars Global Simulant |
| MRO | Mars Reconnaissance Orbiter |
| OWR | Outer Window Region |
| RELAB | Reflectance Experiment Laboratory |
| ROC curve | Receiver Operating Characteristic Curve |
| ROI | Region of Interest |
| SAD | Spectral Angle Distance |
| SAM | Spectral Angle Mapper |
| SASTD | Spatially Adaptive Sparse Representation for Target Detection |
| Serp | Serpentine |
| HSASTD-IBP | Joint the Hapke model and SASTD with IBP |
| SSA | Single-Scattering Albedo |
| STD | Sparse Representation for Target Detection |
| SWIR | Shortwave Infrared |
References
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- Bibring, J.P.; Langevin, Y.; Gendrin, A.; Gondet, B.; Poulet, F.; Berthé, M.; Soufflot, A.; Arvidson, R.; Mangold, N.; Mustard, J. Mars surface diversity as revealed by the OMEGA/Mars Express observations. Science 2005, 307, 1576–1581. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murchie, S.; Arvidson, R.; Bedini, P.; Beisser, K.; Bibring, J.P.; Bishop, J.; Boldt, J.; Cavender, P.; Choo, T.; Clancy, R.T. Compact Reconnaissance Imaging Spectrometer for Mars (CRISM) on Mars Reconnaissance Orbiter (MRO). J. Geophys. Res. Atmos. 2007, 112, 431–433. [Google Scholar] [CrossRef]
- Ehlmann, B.L.; Edwards, C.S. Mineralogy of the Martian Surface. Earth Planet. Sci. 2014, 42, 291–315. [Google Scholar] [CrossRef] [Green Version]
- Murchie, S.L.; Mustard, J.F.; Ehlmann, B.L.; Milliken, R.E.; Bishop, J.L.; Mckeown, N.K.; Dobrea, E.Z.N.; Seelos, F.P.; Buczkowski, D.L.; Wiseman, S.M. A synthesis of Martian aqueous mineralogy after 1 Mars year of observations from the Mars Reconnaissance Orbiter. J. Geophys. Res. Planets 2009, 114, E00D06. [Google Scholar] [CrossRef]
- Carter, J.; Poulet, F.; Bibring, J.P.; Mangold, N.; Murchie, S. Hydrous minerals on Mars as seen by the CRISM and OMEGA imaging spectrometers: Updated global view. J. Geophys. Res. Atmos. 2013, 118, 831–858. [Google Scholar] [CrossRef]
- Mustard, J.F.; Murchie, S.L.; Pelkey, S.M.; Ehlmann, B.L.; Milliken, R.E.; Grant, J.A.; Bibring, J.P.; Poulet, F.; Bishop, J.; Dobrea, E.N. Hydrated silicate minerals on Mars observed by the Mars Reconnaissance Orbiter CRISM instrument. Nature 2008, 454, 305–309. [Google Scholar] [CrossRef]
- Ehlmann, B.L.; Mustard, J.F.; Swayze, G.A.; Clark, R.N.; Bishop, J.L.; Poulet, F.; Des Marais, D.J.; Roach, L.H.; Milliken, R.E.; Wray, J.J.; et al. Identification of hydrated silicate minerals on Mars using MRO-CRISM: Geologic context near Nili Fossae and implications for aqueous alteration. J. Geophys. Res. 2009, 114, 538–549. [Google Scholar] [CrossRef]
- Liu, Y.; Glotch, T.D.; Scudder, N.A.; Kraner, M.L.; Condus, T.; Arvidson, R.E.; Guinness, E.A.; Wolff, M.J.; Smith, M.D. End-member Identification and Spectral Mixture Analysis of CRISM Hyperspectral Data: A Case Study on Southwest Melas Chasma, Mars. J. Geophys. Res. Planets 2016, 121, 2004–2036. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, X. Retrieving the hydrous minerals on Mars by sparse unmixing and the Hapke model using MRO/CRISM data. Icarus 2017, 288, 160–171. [Google Scholar] [CrossRef]
- Wray, J.J.; Murchie, S.L.; Bishop, J.L.; Ehlmann, B.L.; Milliken, R.E.; Wilhelm, M.B.; Seelos, K.D.; Chojnacki, M. Orbital evidence for more widespread carbonate-bearing rocks on Mars. J. Geophys. Res. Planets 2016, 121, 652–677. [Google Scholar] [CrossRef] [Green Version]
- Sun, V.Z.; Milliken, R.E. Ancient and recent clay formation on Mars as revealed from a global survey of hydrous minerals in crater central peaks. J. Geophys. Res. Planets 2015, 120, 2293–2332. [Google Scholar] [CrossRef]
- Pelkey, S.M.; Mustard, J.F.; Murchie, S.; Clancy, R.T.; Wolff, M.; Smith, M.; Milliken, R.; Bibring, J.P.; Gendrin, A.; Poulet, F.; et al. CRISM multispectral summary products: Parameterizing mineral diversity on Mars from reflectance. J. Geophys. Res. 2007, 112, 1–18. [Google Scholar] [CrossRef]
- Viviano-Beck, C.E.; Seelos, F.P.; Murchie, S.L.; Kahn, E.G.; Seelos, K.D.; Taylor, H.W.; Taylor, K.; Ehlmann, B.L.; Wiseman, S.M.; Mustard, J.F.; et al. Revised CRISM spectral parameters and summary products based on the currently detected mineral diversity on Mars. J. Geophys. Res. Planets 2014, 119, 1403–1431. [Google Scholar] [CrossRef] [Green Version]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-Based Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef] [Green Version]
- Poulet, F.; Carter, J.; Bishop, J.L.; Loizeau, D.; Murchie, S.M. Mineral abundances at the final four curiosity study sites and implications for their formation. Icarus 2014, 231, 65–76. [Google Scholar] [CrossRef]
- Lin, H.; Mustard, J.F.; Zhang, X. A methodology for quantitative analysis of hydrated minerals on Mars with large endmember library using CRISM near-infrared data. Planet. Space Sci. 2019, 165, 124–136. [Google Scholar] [CrossRef]
- Manolakis, D.; Truslow, E.; Pieper, M.; Cooley, T. Detection Algorithms in Hyperspectral Imaging Systems: An Overview of Practical Algorithms. IEEE Signal Process. Mag. 2014, 31, 24–33. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral Target Detection: An Overview of Current and Future Challenges. IEEE Signal Process. Mag. 2014, 31, 34–44. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Simultaneous Joint Sparsity Model for Target Detection in Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2011, 8, 676–680. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse Representation for Target Detection in Hyperspectral Imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L. A Sparse Representation-Based Binary Hypothesis Model for Target Detection in Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1346–1354. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, Y.; Zhang, L. Spatially Adaptive Sparse Representation for Target Detection in Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1923–1927. [Google Scholar] [CrossRef]
- Heylen, R.; Parente, M.; Gader, P. A review of nonlinear hyperspectral unmixing methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, X.; Cen, Y. Multi-task Joint Sparse and Low-rank Representation Target Detection for Hyperspectral Image. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1756–1760. [Google Scholar] [CrossRef]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Solid Earth 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Cannon, K.M.; Britt, D.T.; Smith, T.M.; Fritsche, R.F.; Batcheldor, D. Mars global simulant MGS-1: A Rocknest-based open standard for basaltic martian regolith simulants. Icarus 2019, 317, 470–478. [Google Scholar] [CrossRef] [Green Version]
- Allender, E.; Stepinski, T.F. Automatic, exploratory mineralogical mapping of CRISM imagery using summary product signatures. Icarus 2017, 281, 151–161. [Google Scholar] [CrossRef]
- Van Ruitenbeek, F.J.A.; Bakker, W.H.; van der Werff, H.M.A.; Zegers, T.E.; Oosthoek, J.H.P.; Omer, Z.A.; Marsh, S.H.; van der Meer, F.D. Mapping the wavelength position of deepest absorption features to explore mineral diversity in hyperspectral images. Planet. Space Sci. 2014, 101, 108–117. [Google Scholar] [CrossRef]
- Carter, J.; Poulet, F.; Murchie, S.; Bibring, J.P. Automated processing of planetary hyperspectral datasets for the extraction of weak mineral signatures and applications to CRISM observations of hydrated silicates on Mars. Planet. Space Sci. 2013, 76, 53–67. [Google Scholar] [CrossRef]
- Combe, J.P.; Mouélic, S.L.; Sotin, C.; Gendrin, A.; Mustard, J.F.; Deit, L.L.; Launeau, P.; Bibring, J.P.; Gondet, B.; Langevin, Y. Analysis of OMEGA/Mars Express data hyperspectral data using a Multiple-Endmember Linear Spectral Unmixing Model (MELSUM): Methodology and first results. Planet. Space Sci. 2008, 56, 951–975. [Google Scholar] [CrossRef]
- Gilmore, M.S.; Thompson, D.R.; Anderson, L.J.; Karamzadeh, N.; Mandrake, L.; Castaño, R. Superpixel segmentation for analysis of hyperspectral data sets, with application to Compact Reconnaissance Imaging Spectrometer for Mars data, Moon Mineralogy Mapper data, and Ariadnes Chaos, Mars. J. Geophys. Res. Planets 2011, 116, E07001. [Google Scholar] [CrossRef]
- Schmidt, F.; Bourguignon, S.; Mouelic, S.L.; Dobigeon, N. Accuracy and Performance of Linear Unmixing Techniques for Detecting Minerals on OMEGA/Mars Express. In Proceedings of the Workshop on Hyperspectral Image & Signal Processing: Evolution in Remote Sensing, Lisbon, Portugal, 6–9 June 2011; pp. 1–4. [Google Scholar]
- Farrand, W.H.; Harsanyi, J.C. Mapping the distribution of mine tailings in the Coeur d’Alene River Valley, Idaho, through the use of a constrained energy minimization technique. Remote Sens. Environ. 1997, 59, 64–76. [Google Scholar] [CrossRef]
- Ehlmann, B.L.; Mustard, J.F.; Murchie, S.L. Geologic setting of serpentine deposits on Mars. Geophys. Res. Lett. 2010, 37, 53–67. [Google Scholar] [CrossRef] [Green Version]
- Leask, E.K.; Ehlmann, B.L.; Dundar, M.M.; Murchie, S.L.; Seelos, F.P. Challenges in the Search for Perchlorate and Other Hydrated Minerals With 2.1-mu m Absorptions on Mars. Geophys. Res. Lett. 2018, 45, 12180–12189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGuire, P.C.; Bishop, J.L.; Brown, A.J.; Fraeman, A.A.; Marzo, G.A.; Frank Morgan, M.; Murchie, S.L.; Mustard, J.F.; Parente, M.; Pelkey, S.M.; et al. An improvement to the volcano-scan algorithm for atmospheric correction of CRISM and OMEGA spectral data. Planet. Space Sci. 2009, 57, 809–815. [Google Scholar] [CrossRef] [Green Version]
- Goudge, T.A.; Mustard, J.F.; Head, J.W.; Salvatore, M.R.; Wiseman, S.M. Integrating CRISM and TES hyperspectral data to characterize a halloysite-bearing deposit in Kashira crater, Mars. Icarus 2015, 250, 165–187. [Google Scholar] [CrossRef]
- Mustard, J.F.; Pieters, C.M. Photometric phase functions of common geologic minerals and applications to quantitative analysis of mineral mixture reflectance spectra. J. Geophys. Res. Solid Earth 1989, 94, 13619–13634. [Google Scholar] [CrossRef]
- Matteoli, S.; Diani, M.; Theiler, J. An Overview of Background Modeling for Detection of Targets and Anomalies in Hyperspectral Remotely Sensed Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2317–2336. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)—interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Zou, Z.; Shi, Z. Hierarchical Suppression Method for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 330–342. [Google Scholar] [CrossRef]
- Shi, Y.; Lei, J.; Yin, Y.; Cao, K.; Li, Y.; Chang, C.-I. Discriminative feature learning with distance constrained stacked sparse autoencoder for hyperspectral target detection. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1462–1466. [Google Scholar] [CrossRef]













| Name | Meaning | Formulation [14] | Rationale | Caveats |
|---|---|---|---|---|
| BD1900 | 1.9 μm H2O band depth | H2O | ||
| D2200 | 2.2 μm dropoff | Al-OH minerals | Chlorite, Prehnite | |
| D2300 | 2.3 μm dropoff | Hydroxylated Fe, Mg silicates strongly > 0 | Mg-Carbonate |
| Dataset | Reflectance | SSA | |||
|---|---|---|---|---|---|
| Algorithm | AUC | Time | AUC | Time | |
| CEM | 0.5090 | 0.19 | 0.5924 | 0.20 | |
| MF | 0.5584 | 0.32 | 0.5971 | 0.41 | |
| hCEM | 0.5848 | 1.86 | 0.5998 | 1.93 | |
| STD | 0.7455 | 130.78 | 0.8025 | 139.27 | |
| SASTD | 0.7469 | 161.62 | 0.8121 | 160.28 | |
| SASTD-IBP | 0.7799 | 179.34 | 0.8965 | 181.79 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Zhang, X.; Mustard, J.; Tarnas, J.; Lin, H.; Liu, Y. Joint Hapke Model and Spatial Adaptive Sparse Representation with Iterative Background Purification for Martian Serpentine Detection. Remote Sens. 2021, 13, 500. https://doi.org/10.3390/rs13030500
Wu X, Zhang X, Mustard J, Tarnas J, Lin H, Liu Y. Joint Hapke Model and Spatial Adaptive Sparse Representation with Iterative Background Purification for Martian Serpentine Detection. Remote Sensing. 2021; 13(3):500. https://doi.org/10.3390/rs13030500
Chicago/Turabian StyleWu, Xing, Xia Zhang, John Mustard, Jesse Tarnas, Honglei Lin, and Yang Liu. 2021. "Joint Hapke Model and Spatial Adaptive Sparse Representation with Iterative Background Purification for Martian Serpentine Detection" Remote Sensing 13, no. 3: 500. https://doi.org/10.3390/rs13030500
APA StyleWu, X., Zhang, X., Mustard, J., Tarnas, J., Lin, H., & Liu, Y. (2021). Joint Hapke Model and Spatial Adaptive Sparse Representation with Iterative Background Purification for Martian Serpentine Detection. Remote Sensing, 13(3), 500. https://doi.org/10.3390/rs13030500