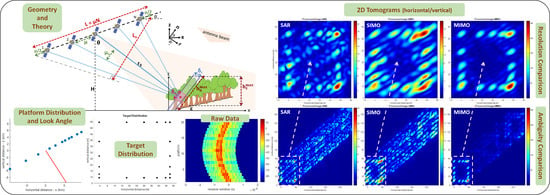
Tomographic Performance of Multi-Static Radar Formations: Theory and Simulations
Abstract
:1. Introduction
2. Theory of Tomographic Imaging
2.1. Resolution
2.2. Ambiguities
2.3. Minimum Number of Platforms
3. Tomography Simulations
3.1. Raw Data Generation in 1D
3.2. Tomogram Generation in 1D
3.3. Raw Data Generation in 2D
3.4. Tomogram Generation in 2D
4. Results
4.1. Comparison of SAR, SIMO, and MIMO Modes via Analytical Equations
4.2. 1D Simulations
4.3. 2D Simulations
4.3.1. Example 1: Reference Scenario
4.3.2. Example 2: Changing SNR
4.3.3. Example 3: Changing Frequency and Bandwidth
4.3.4. Example 4: Changing PRI and Pulse Width
4.3.5. Example 5: Changing Altitude
4.3.6. Example 6: Changing Baseline Tilt and Look Angle
4.3.7. Example 7: Changing Number of Platforms and Tomographic Aperture
4.3.8. Example 8: Changing Tomographic Aperture and Platform Spacing (Equal Spacing)
4.3.9. Example 9: Changing Tomographic Aperture and Platform Spacing (Unequal Spacing)
5. Discussion
- Larger baseline, same spacing results in same ambiguity, better resolution, more platforms.
- Same baseline, larger spacing results in worse ambiguity, same resolution, less platforms.
- Larger baseline, larger spacing results in worse ambiguity, better resolution, same number of platforms
- Smaller baseline, smaller spacing results in better ambiguity, worse resolution, same number of platforms
- SAR has the best resolution but the worst ambiguity performance. In addition, it has lower SNR and higher sidelobes than MIMO. Similar to MIMO, SAR requires all platforms to have TX capability. However, unlike MIMO, SAR does not require clock synchronization as each platform receives its own signal. SAR requires less data size than MIMO.
- SIMO has better ambiguity performance than SAR but the worst resolution performance. Nevertheless, SIMOe has as good target resolving capability as SAR (even though its resolution is worse than SAR). On the other hand, SIMOm has the worst resolving capability. In addition, SIMO has lower SNR and higher sidelobes than MIMO. To its advantage, SIMO requires only one platform with TX capability which translates into lower costs. Furthermore, TX/RX timing and clock synchronization are less challenging in SIMO than MIMO. SIMO requires less data size than MIMO.
- MIMO has the best overall performance in terms of tomographic SNR, resolution, ambiguity, and sidelobes. Even though its resolution is not the best, it is superior in terms of SNR and sidelobes. Its ambiguities can also be reduced by nonlinear platform spacing at the expense of sidelobes since it can tolerate higher sidelobes. However, MIMO requires all platforms to have TX capability as well as clock synchronization among platforms to synchronize timing and preserve phase coherence both of which translate into higher costs. MIMO also requires either orthogonal codes to be able to transmit simultaneously or more complex TX/RX timing to avoid eclipsing of multiple TX/RX pulses. Moreover, MIMO data (before tomographic processing) require significantly larger data size (depending on the number of platforms), which poses requirements on downlink capacity and/or onboard processing.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jordan, R. The Seasat-A synthetic aperture radar system. IEEE J. Ocean. Eng. 1980, 5, 154–164. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–380. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
- Bamler, P.H.R. Synthetic Aperture Radar Interferometry. Inverse Probl. 1998, 14, 1–54. [Google Scholar] [CrossRef]
- Gini, F.; Lombardini, F.; Montanari, M. Layover solution in multibaseline SAR interferometry. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 1344–1356. [Google Scholar] [CrossRef]
- Reigber, A.; Moreira, A. First demonstration of airborne SAR tomography using multibaseline L-band data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2142–2152. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Lombardini, F.; Montanari, M.; Gini, F. Reflectivity estimation for multibaseline interferometric radar imaging of layover extended sources. IEEE Trans. Signal Process. 2003, 51, 1508–1519. [Google Scholar] [CrossRef]
- Fornaro, G.; Serafino, F.; Soldovieri, F. Three-dimensional focusing with multipass SAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 507–517. [Google Scholar] [CrossRef]
- Pasquali, P.; Prati, C.; Rocca, F.; Seymour, M.; Fortuny, J.; Ohlmer, E.; Sieber, A. A 3-D SAR experiment with EMSL data. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium, IGARSS ’Quantitative Remote Sensing for Science and Applications, Firenze, Italy, 10–14 July 1995; Volume 1, pp. 784–786. [Google Scholar]
- Farhat, N.H.; Werner, C.L.; Chu, T.H. Prospects for three-dimensional projective and tomographic imaging radar networks. Radio Sci. 1984, 19, 1347–1355. [Google Scholar] [CrossRef]
- Homer, J.; Longstaff, I.; Callaghan, G. High resolution 3-D SAR via multi-baseline interferometry. In Proceedings of the IGARSS ’96. 1996 International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31 May 1996; IEEE: New York, NY, USA, 2002. [Google Scholar]
- Aghababaee, H.; Ferraioli, G.; Ferro-Famil, L.; Huang, Y.; D’Alessandro, M.M.; Pascazio, V.; Schirinzi, G.; Tebaldini, S. Forest SAR Tomography: Principles and Applications. IEEE Geosci. Remote Sens. Mag. 2020, 8, 30–45. [Google Scholar] [CrossRef]
- Tebaldini, S. Single and Multipolarimetric SAR Tomography of Forested Areas: A Parametric Approach. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2375–2387. [Google Scholar] [CrossRef]
- Minh, D.H.T.; Le Toan, T.; Rocca, F.; Tebaldini, S.; D’Alessandro, M.M.; Villard, L. Relating P-Band Synthetic Aperture Radar Tomography to Tropical Forest Biomass. IEEE Trans. Geosci. Remote Sens. 2013, 52, 967–979. [Google Scholar] [CrossRef]
- Pardini, M.; Tello, M.; Cazcarra-Bes, V.; Papathanassiou, K.P.; Hajnsek, I. L- and P-Band 3-D SAR Reflectivity Profiles versus Lidar Waveforms: The AfriSAR Case. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3386–3401. [Google Scholar] [CrossRef]
- Frey, O.; Meier, E. 3-D Time-Domain SAR Imaging of a Forest Using Airborne Multibaseline Data at L- and P-Bands. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3660–3664. [Google Scholar] [CrossRef]
- Yu, Y.; D’Alessandro, M.M.; Tebaldini, S.; Liao, M. Signal Processing Options for High Resolution SAR Tomography of Natural Scenarios. Remote Sens. 2020, 12, 10. [Google Scholar]
- Huang, Y.; Ferro-Famil, L.; Reigber, A. Under-Foliage Object Imaging Using SAR Tomography and Polarimetric Spectral Estimators. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2213–2225. [Google Scholar] [CrossRef] [Green Version]
- Cazcarra-Bes, V.; Pardini, M.; Tello, M.; Papathanassiou, K.P. Comparison of Tomographic SAR Reflectivity Reconstruction Algorithms for Forest Applications at L-band. IEEE Trans. Geosci. Remote Sens. 2019, 58, 147–164. [Google Scholar] [CrossRef]
- Aguilera, E.; Nannini, M.; Reigber, A. A Data-Adaptive Compressed Sensing Approach to Polarimetric SAR Tomography of Forested Areas. IEEE Geosci. Remote Sens. Lett. 2012, 10, 543–547. [Google Scholar] [CrossRef]
- Joerg, H.; Pardini, M.; Hajnsek, I.; Papathanassiou, K.P. 3-D Scattering Characterization of Agricultural Crops at C-Band Using SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3976–3989. [Google Scholar] [CrossRef]
- Lombardini, F. Differential tomography: A new framework for SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2004, 43, 37–44. [Google Scholar] [CrossRef]
- Lombardini, F.; Pardini, M. Superresolution Differential Tomography: Experiments on Identification of Multiple Scatterers in Spaceborne SAR Data. IEEE Trans. Geosci. Remote Sens. 2011, 50, 1117–1129. [Google Scholar] [CrossRef]
- Pauciullo, A.; Reale, D.; De Maio, A.; Fornaro, G. Detection of Double Scatterers in SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3567–3586. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Let’s Do the Time Warp: Multicomponent Nonlinear Motion Estimation in Differential SAR Tomography. IEEE Geosci. Remote Sens. Lett. 2011, 8, 735–739. [Google Scholar] [CrossRef] [Green Version]
- Siddique, M.A.; Wegmüller, U.; Hajnsek, I.; Frey, O. Single-Look SAR Tomography as an Add-On to PSI for Improved Deformation Analysis in Urban Areas. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6119–6137. [Google Scholar] [CrossRef]
- Budillon, A.; Diaz-Fuentes, G. GLRT Based on Support Estimation for Multiple Scatterers Detection in SAR Tomography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 1086–1094. [Google Scholar] [CrossRef]
- Banda, F.; Dall, J.; Tebaldini, S. Single and Multipolarimetric P-Band SAR Tomography of Subsurface Ice Structure. IEEE Trans. Geosci. Remote Sens. 2015, 54, 2832–2845. [Google Scholar] [CrossRef]
- Rekioua, B.; Davy, M.; Ferro-Famil, L.; Tebaldini, S. Snowpack permittivity profile retrieval from tomographic SAR data. Comptes Rendus Phys. 2017, 18, 57–65. [Google Scholar] [CrossRef]
- Xu, X.; Baldi, C.A.; De Bleser, J.-W.; Lei, Y.; Yueh, S.; Esteban-Fernandez, D. Multi-Frequency Tomography Radar Observations of Snow Stratigraphy at Fraser During SnowEx. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: New York, NY, USA, 2018; pp. 6269–6272. [Google Scholar]
- Frey, O.; Werner, C.L.; Wiesmann, A. Tomographic profiling of the structure of a snow pack at X-/Ku-Band using SnowScat in SAR mode. In Proceedings of the 2015 European Radar Conference (EuRAD), Paris, France, 9–11 September 2015; IEEE: New York, NY, USA, 2015; pp. 21–24. [Google Scholar]
- Morrison, K.; Bennett, J. Tomographic Profiling—A Technique for Multi-Incidence-Angle Retrieval of the Vertical SAR Backscattering Profiles of Biogeophysical Targets. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1350–1355. [Google Scholar] [CrossRef]
- Frey, O.; Werner, C.L.; Caduff, R.; Wiesmann, A. Tomographic Profiling with Snowscat within the ESA Snowlab Campaign: Time Series of Snow Profiles Over three Snow Seasons. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: New York, NY, USA, 2018; pp. 6512–6515. [Google Scholar]
- Frey, O.; Meier, E. Analyzing Tomographic SAR Data of a Forest with Respect to Frequency, Polarization, and Focusing Technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3648–3659. [Google Scholar] [CrossRef] [Green Version]
- Tebaldini, S.; Rocca, F. Multibaseline Polarimetric SAR Tomography of a Boreal Forest at P- and L-Bands. IEEE Trans. Geosci. Remote Sens. 2011, 50, 232–246. [Google Scholar] [CrossRef]
- Ulander, L.M.H.; Monteith, A.R.; Soja, M.J.; Eriksson, L.E.B. Multiport Vector Network Analyzer Radar for Tomographic Forest Scattering Measurements. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1897–1901. [Google Scholar] [CrossRef]
- Lavalle, M.; Hawkins, B.; Hensley, S. Tomographic imaging with UAVSAR: Current status and new results from the 2016 AfriSAR campaign. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: New York, NY, USA, 2017; pp. 2485–2488. [Google Scholar]
- Khati, U.; LaValle, M.; Singh, G. Spaceborne tomography of multi-species Indian tropical forests. Remote Sens. Environ. 2019, 229, 193–212. [Google Scholar] [CrossRef]
- Cloude, S.R. Polarization coherence tomography. Radio Sci. 2006, 41. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef] [Green Version]
- Shiroma, G.H.X.; Lavalle, M. Digital Terrain, Surface, and Canopy Height Models From InSAR Backscatter-Height Histograms. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3754–3777. [Google Scholar] [CrossRef]
- Pardini, M.; Armston, J.; Qi, W.; Lee, S.K.; Tello, M.; Bes, V.C.; Choi, C.; Papathanassiou, K.P.; Dubayah, R.O.; Fatoyinbo, L.E. Early Lessons on Combining Lidar and Multi-baseline SAR Measurements for Forest Structure Characterization. Surv. Geophys. 2019, 40, 803–837. [Google Scholar] [CrossRef]
- D’Alessandro, M.M.; Tebaldini, S. Digital Terrain Model Retrieval in Tropical Forests Through P-Band SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6774–6781. [Google Scholar] [CrossRef]
- Krieger, G.; Zonno, M.; Rodriguez-Cassola, M.; Lopez-Dekker, P.; Mittermayer, J.; Younis, M.; Huber, S.; Villano, M.; De Almeida, F.Q.; Prats-Iraola, P.; et al. MirrorSAR: A fractionated space radar for bistatic, multistatic and high-resolution wide-swath SAR imaging. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: New York, NY, USA, 2017; pp. 149–152. [Google Scholar]
- Grasso, M.; Renga, A.; Fasano, G.; Graziano, M.; Grassi, M.; Moccia, A. Design of an end-to-end demonstration mission of a Formation-Flying Synthetic Aperture Radar (FF-SAR) based on microsatellites. Adv. Space Res. 2020. [Google Scholar] [CrossRef]
- Nannini, M.; Scheiber, R.; Moreira, A. Estimation of the Minimum Number of Tracks for SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2009, 47, 531–543. [Google Scholar] [CrossRef]
- Frey, O.; Meier, E.; Hajnsek, I. On the sensitivity of measured backscattering properties to variations of incidence angle and baselines in tomographic SAR data. In Proceedings of the 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Korea, 26–30 September 2011. [Google Scholar]
- Richards, M.A.; Scheer, J.A.; Holm, W.A. (Eds.) Principles of Modern Radar: Basic Principles; Institution of Engineering and Technology: Stevenage, UK, 2010. [Google Scholar]
- Krieger, G.; Rommel, T.; Moreira, A. MIMO-SAR Tomography. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016. [Google Scholar]
- Mittermayer, J.; Krieger, G.; Moreira, A. Concepts and Applications of Multi-static MirrorSAR Systems. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; IEEE: New York, NY, USA, 2020; pp. 1–6. [Google Scholar]
- Nannini, M.; Scheiber, R. Time Domain Beamforming Algorithm for SAR Tomography. In Proceedings of the EUSAR, 2006: 6th European Conference on Synthetic Aperture Radar, Dresden, Germany, 16–18 May 2006. [Google Scholar]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]



































| Parameter | Value |
|---|---|
| Frequency | 1.2 GHz |
| Altitude | 700 km |
| Number of Targets | 1 |
| Number of Platforms | 12 |
| Tomographic Aperture | 16.5 km |
| Platform Spacing | 1500 m |
| Target Location | 0 m |
| Scene Extend | 150 m |
| Scene Resolution | 1 cm |
| Theoretical Resolution | Measured Resolution | Theoretical Ambiguity Location | Measured Ambiguity Location | Measured PSLR | |||
|---|---|---|---|---|---|---|---|
| Rayleigh | 3.9 dB | Rayleigh | 3.9 dB | ||||
| SAR | 4.9 m | 4.9 m | 4.9 m | 4.9 m | 58 m | 58 m | −13 dB |
| SIMO | 9.7 m | 9.7 m | 9.7 m | 9.7 m | 117 m | 117 m | −13 dB |
| MIMO | 9.7 m | 7.0 m | 9.7 m | 7.0 m | 117 m | 117 m | −26 dB |
| Resolution along Elevation | PSLR | |||||
|---|---|---|---|---|---|---|
| No Window | Taylor Window (−40 dB, nbar = 5) | No Window | Taylor Window (−40 dB, nbar = 5) | |||
| Rayleigh | 3.9 dB | Rayleigh | 3.9 dB | |||
| SAR | 4.9 m | 4.9 m | 17.7 m | 6.9 m | −13 dB | −38 dB |
| SIMOe | 9.7 m | 9.7 m | 19.4 m | 9.7 m | −13 dB | −13 dB |
| SIMOm | 9.7 m | 9.7 m | 35.4 m | 13.7 m | −13 dB | −38 dB |
| MIMO | 9.7 m | 7.0 m | 19.4 m | 8.1 m | −26 dB | −28 dB |
| Parameter | Value |
|---|---|
| Frequency | 1.2 GHz |
| Bandwidth | 40 MHz |
| Pulse Width | 10 us |
| PRI | 100 us |
| Altitude | 700 km |
| Number of Platforms | 12 |
| Tomographic Aperture | 11 km |
| Platform Spacing | 1 km |
| Baseline Tilt | 30° |
| Look Angle | 30° |
| SNR | 50 dB |
| Parameter | Value |
|---|---|
| Frequency | 1.2 GHz |
| Bandwidth | 40 MHz |
| Pulse Width | 10 us |
| PRI | 100 us |
| Altitude | 700 km |
| Number of Platforms | 12 |
| Tomographic Aperture | 11 km |
| Platform Spacing | 1 km |
| Baseline Tilt | 30° |
| Look Angle | 30° |
| SNR | 20 dB |
| Parameter | Value |
|---|---|
| Frequency | 0.6 GHz |
| Bandwidth | 20 MHz |
| Pulse Width | 10 us |
| PRI | 100 us |
| Altitude | 700 km |
| Number of Platforms | 12 |
| Tomographic Aperture | 11 km |
| Platform Spacing | 1 km |
| Baseline Tilt | 30° |
| Look Angle | 30° |
| SNR | 50 dB |
| Parameter | Value |
|---|---|
| Frequency | 1.2 GHz |
| Bandwidth | 40 MHz |
| Pulse Width | 0.5 us |
| PRI | 1 us |
| Altitude | 700 km |
| Number of Platforms | 12 |
| Tomographic Aperture | 11 km |
| Platform Spacing | 1 km |
| Baseline Tilt | 30° |
| Look Angle | 30° |
| SNR | 50 dB |
| Parameter | Value |
|---|---|
| Frequency | 1.2 GHz |
| Bandwidth | 40 MHz |
| Pulse Width | 10 us |
| PRI | 100 us |
| Altitude | 400 km |
| Number of Platforms | 12 |
| Tomographic Aperture | 11 km |
| Platform Spacing | 1 km |
| Baseline Tilt | 30° |
| Look Angle | 30° |
| SNR | 50 dB |
| Parameter | Value |
|---|---|
| Frequency | 1.2 GHz |
| Bandwidth | 40 MHz |
| Pulse Width | 10 us |
| PRI | 100 us |
| Altitude | 700 km |
| Number of Platforms | 12 |
| Tomographic Aperture | 11 km |
| Platform Spacing | 1 km |
| Baseline Tilt | 50° |
| Look Angle | 50° |
| SNR | 50 dB |
| Parameter | Value |
|---|---|
| Frequency | 1.2 GHz |
| Bandwidth | 40 MHz |
| Pulse Width | 10 us |
| PRI | 100 us |
| Altitude | 700 km |
| Number of Platforms | 6 |
| Tomographic Aperture | 5 km |
| Platform Spacing | 1 km |
| Baseline Tilt | 30° |
| Look Angle | 30° |
| SNR | 50 dB |
| Parameter | Value |
|---|---|
| Frequency | 1.2 GHz |
| Bandwidth | 40 MHz |
| Pulse Width | 10 us |
| PRI | 100 us |
| Altitude | 700 km |
| Number of Platforms | 12 |
| Tomographic Aperture | 22 km |
| Platform Spacing | 2 km |
| Baseline Tilt | 30° |
| Look Angle | 30° |
| SNR | 50 dB |
| Parameter | Value |
|---|---|
| Frequency | 1.2 GHz |
| Bandwidth | 40 MHz |
| Pulse Width | 10 us |
| PRI | 100 us |
| Altitude | 700 km |
| Number of Platforms | 12 |
| Tomographic Aperture | 22 km |
| Platform Spacing | variable |
| Baseline Tilt | 30° |
| Look Angle | 30° |
| SNR | 50 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seker, I.; Lavalle, M. Tomographic Performance of Multi-Static Radar Formations: Theory and Simulations. Remote Sens. 2021, 13, 737. https://doi.org/10.3390/rs13040737
Seker I, Lavalle M. Tomographic Performance of Multi-Static Radar Formations: Theory and Simulations. Remote Sensing. 2021; 13(4):737. https://doi.org/10.3390/rs13040737
Chicago/Turabian StyleSeker, Ilgin, and Marco Lavalle. 2021. "Tomographic Performance of Multi-Static Radar Formations: Theory and Simulations" Remote Sensing 13, no. 4: 737. https://doi.org/10.3390/rs13040737
APA StyleSeker, I., & Lavalle, M. (2021). Tomographic Performance of Multi-Static Radar Formations: Theory and Simulations. Remote Sensing, 13(4), 737. https://doi.org/10.3390/rs13040737