Modeling and Simulation of Very High Spatial Resolution UXOs and Landmines in a Hyperspectral Scene for UAV Survey
Abstract
:1. Introduction
1.1. Motivation
1.2. Possible Terrain Case
1.3. The Civilian Aerial Survey Technologies for Explosive Threats
“No export restrictions. Platforms as small as possible. We want to operate equipment ourselves, not rely on external personnel. In the short term, detection capabilities are more important than the interface. Need to see real evidence of value before committing to field trials. Detection is only one stage of the clearance process. The combination of sensors and platforms must offer some advantage in terms of reduced false alarms or detection ability, not just the speed of coverage. Vegetation cover will be a major limiting factor in many places usually we cannot remove this in advance because of safety, cost, or environmental damage. The abilities of the sensor/data processing are what matters. Possible sensors: Thermal IR, Hyperspectral, Magnetometers?”[11].
1.4. The Direct Detection of Explosive Targets and Detection of Their Secondary Indicators
1.5. Hyperspectral Sensors and Platforms
1.5.1. Sensors
1.5.2. Ground-Based and Aerial Platforms
1.5.3. Portable Carry-on and Handheld Hyperspectral Cameras
2. Materials and Methods
2.1. The True Hyperspectral Data Cubes of UXO on the Ground
2.2. Landmines and Plastic Objects, Whose Spectra Are Provided by Point-Like Measurements with ASD





2.3. Hyperspectral Cubes of the Terrain Acquired by UHD-185
2.4. Simulation of the Spatial Distribution of the Explosive Objects
2.5. The Implanting Spectral Data of Explosive Targets in the Hyperspectral Scene of the Terrain
2.5.1. Spectral Angle Mapping
2.5.2. Target Simulation Options
- 1.
- The true spectral data of explosive targets, measured by a hyperspectral imaging scanner, and pixels matched to pixels of terrain scene spectra.
- 2.
- The average spectral data of explosive targets measured by a point measuring spectrometer. This kind of target’s spectral data for land mines has only appeared in the literature.
- 3.
- Modeling the partial random obscuring of explosive targets on the ground surface.
- 4.
- Modeling the partial mixing spectra of the explosive targets and the background.
- 5.
- Simulation of random spectral data in the interval between the maximum and minimum of the spectral data of explosive targets, measured by a point measuring spectrometer. We tested the random generation of data using a uniform probability distribution and considered several other distributions.
2.5.3. Modeling the Obscured Spectra of the Explosive Target and the Overlayed Target’s Spectra and the Spectra of Background
2.6. Model of Target Detection
3. Results
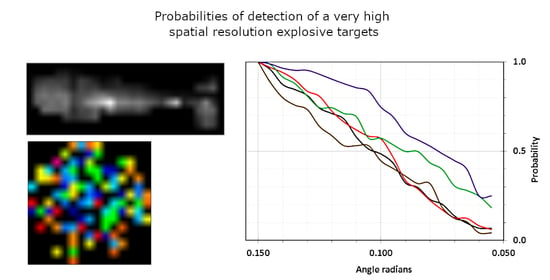
3.1. Probability of Target Detection POD, Confidence Intervals
3.2. Polynomial Approximations of POD, PODupper, and PODlower
3.3. Simulation of Target Placement
3.4. SAM Detection Endmembers and Results
4. Discussion
- -
- The true spectral data of the UXO and landmines were measured by ground-based hyperspectral imaging sensors, with ground resolving distance (GRD) of 0.954 mm.
- -
- The spectral data of the terrain—that is, of the minefields and their surroundings—were acquired by UAV with hyperspectral imaging sensors, with GRD of 18.68 mm.
- -
- The best value of GRD target/terrain ratio was 0.05058 (or 5.058%) for the available explosive targets and terrain spectral images. Smaller values of this ratio cannot provide acceptable outcomes.
- -
- Without interaction with its neighborhood, such that the whole area of the target was visible to the imaging hyperspectral sensor.
- -
- The area of the target was partially hidden or obscured or covered by terrain (for which, we used the term obscured).
- -
- The spectrum of a target was mixed or overlaid by the spectra of terrain surface (e.g., partially by soil, sand, gravel, vegetation; for this, we used the term overlaid).
5. Conclusions
- 1.
- The motivation for our research into methods for modeling and simulating the implantation of spectral data of explosive targets into terrain spectral data was caused by the lack of civilian (or public military) hyperspectral data, regarding the considered explosive devices, in a realistic, non-laboratory environment. The lack of considered data can be compensated for by using the developed modeling and simulation methods.
- 2.
- The empirical research presented started with taking measurements using imaging hyperspectral sensors, line scanners, and snapshot cameras onboard a UAV and on a ground-based gantry, considering terrain, unexploded ordnances (UXO), and landmines on the ground surface.
- 3.
- The endmembers of explosive targets should be acquired with an imaging sensor having a very high spatial resolution. For artillery shells, bullets, cluster munitions, mortar mines, and small UXOs, we collected 19,251–45,661 spectral samples. For other types of UXO, these data will differ.
- 4.
- The implantation of targets into terrain spectra was done after decreasing the spatial dimensions of the targets and spatially matching their pixels to pixels of the terrain. In the considered cases, the spatial decrease was to 5.058% of the original dimension. The corresponding number of endmembers ranged from 52 to 108; for other types of UXO, this number will be different.
- 5.
- In this study, we demonstrated, for the first time, that larger values of spectral angle mapping classification outcomes are achieved if the endmembers are used from smaller (spatially decreased) explosive targets, and not from full-scale targets.
- 6.
- If the area of the target is partially hidden or obscured, or if the spectra of a target and terrain are mixed or overlaid, the variability of the SAM data has different behavior.
- 7.
- The SAM classifier was used as the detector, where its outputs were considered as a binary outcome of the Bernoulli statistical model, along with its confidence intervals.
- 8.
- Further research should analyze more terrain spectral images, a statistically relevant number of simulated explosive targets, and a variety of terrain–targets spectral influence.
- 9.
- The empirical and analytical findings of this study provide a new understanding of the hyperspectral behavior of UXOs and landmines in natural environments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Target Spectra Overlaid with 10% of the Terrain 147 Spectra




Appendix B. Targets Obstructed by 25.7% in Terrain 227




Appendix C. Terrain with Several Targets


References
- Dorn, A.W. Eliminating hidden killers: How can technology help humanitarian demining? Stab. Int. J. Secur. Dev. 2019, 8, 5. [Google Scholar] [CrossRef] [Green Version]
- Asylbek Kyzy, G.; Jung, Y.; Rapillard, P.; Hofmann, U. Geneva International Centre for Humanitarian Demining; SIPRI. In Global Mapping and Analysis of Anti-Vehicle Mine Incidents in 2017; Geneva International Centre for Humanitarian Demining (GICHD): Geneva, Switzerland, 2018. [Google Scholar]
- Geneva International Centre for Humanitarian Demining. IMAS 08.10. Non-Technical Survey 2009; Geneva International Centre for Humanitarian Demining: Geneva, Switzerland, 2017. [Google Scholar]
- Mats, H. Norwegian peoples IRAQ drone use and lessons learned. Norwegian People’s Aid Workshop on Lessons Learned from the Use of Unmannedaerial Vehicles for the Identification and Assessment of Explosive Devices Threats, Presentation, Podgorica, Montenegro, 16–17 October 2019.
- Mats, H. Video acquired by RPAS. In Norwegian People’s Aid Workshop on Lessons Learned from the Use of Unmannedaerial Vehicles for the Identification and Assessment of Explosive Devices Threats, Podgorica, Montenegro, 16–17 October 2019.
- United Nations: Department of Peacekeeping Operations, Department of Field Support. Guidelines on Improvised Explosive Devices (IED) Threat Mitigation in Mission Settings; United Nations, Department of Peacekeeping Operations, Department of Field Support: New York, NY, USA, 2018. [Google Scholar]
- Kalbarczyk, M. Eda Ied Detection (IEDDET) Programme, Presentation. Available online: http://www.irsd.be/website/images/images/Activites/Colloques/presentation/2016-05-17/05-Mr-Marek-KALBARCZYK.pdf (accessed on 10 February 2020).
- Shutte, K.; Sahli, H.; Schrottmayer, D.; Eisl, M.; Varas, F.J.; Bajic, M.; Uppsal, M.; den Breejen, E. ARC: A camcopter based minefield detection system. In Proceedings of the 5th International Airborne Remote Sensing Conference, San Francisco, CA, USA, 17–20 September 2001. [Google Scholar]
- Toolbox Implementation for Removal of Anti-Personnel Mines, Sub-Munitions and UXO—TIRAMISU, EU FP7 Project 2012–2015, Grant Agreement Number 284747. Available online: http://www.fp7-tiramisu.eu/ (accessed on 9 January 2021).
- Fardoulis, J. Drones in HMA lessons from the field 2019. In Proceedings of the 7th Mine Action Technology Workshop, GCIHD, Basel, Switzerland, 7–8 November 2019. [Google Scholar]
- Nevard, M.; Mansel, R.; Torbet, N. Use of aerial imagery in urban survey & use of RPASs in mine Action—Lessons learned from six countries. In Proceedings of the 7th Mine Action Technology Workshop, GCIHD, Basel, Switzerland, 7–8 November 2019. [Google Scholar]
- Lisica, D. Evaluation on use of UAVs in-country assessment of suspected hazardous areas in Bosnia and Herzegovina 2019. In Proceedings of the Norwegian People’s Aid Workshop on Lessons Learned from the Use of Unmanned Aerial Vehicles for the Identification and Assessment of Explosive Devices Threats, Podgorica, Montenegro, 16–17 October 2019. [Google Scholar]
- McFee, J.E.; Ripley, H.T. Detection of buried land mines using a casi hyperspectral imager. In Detection and Remediation Technologies for Mines and Minelike Targets II; International Society for Optics and Photonics: San Diego, CA, USA, 1997; Volume 3079, pp. 738–749. [Google Scholar]
- Yoresh, A.B. Mine detection by air photography. In Proceedings of the 7th International Symposium; Humanitarian Demining; HCR Center for testing, development and training, Šibenik, Croatia, 27–30 April 2010; Volume 27. [Google Scholar]
- Yoresh, A.B. Identification of minefields by aerial photography 2010. In Proceedings of the Third Mine Action Technology Workshop, Geneva, Switzerland, 6–8 September 2010. [Google Scholar]
- Geneva International Centre for Humanitarian Demining. Geomine Demonstration Test 2012/2013; Geneva International Centre for Humanitarian Demining: Geneva, Switzerland, 2013. [Google Scholar]
- Bajic, M.; Ivelja, T.; Brook, A. Development of a hyperspectral non -technical survey of the minefields from the UAV and the helicopter. J. Conv. Weapons Destr. 2017, 21, 11. [Google Scholar]
- Bajić, M.; Krajnović, M.; Brook, A.; Ivelja, T. Ground vehicle based system for hyperspectral measurement of minefields. In Book of Papers—International Symposium “Mine Action”; HCR Center for Testing, Development and Training: Zagreb, Croatia, 2014; p. 13. [Google Scholar]
- Manley, P.V.; Sagan, V.; Fritschi, F.B.; Burken, J.G. Remote sensing of explosives-induced stress in plants: Hyperspectral imaging analysis for remote detection of unexploded threats. Remote Sens. 2019, 11, 1827. [Google Scholar] [CrossRef] [Green Version]
- Smit, R.; Schmitz, P.; du Plooy, N.; Cooper, A.; van Dyk, T.; Smit, E.; Ramaloko, P. The influence of explosives on plants using in-situ hyperspectral data, Presentation. In Proceedings of the 5th UNMAS/GICHD Bi-Annual Technology Workshop, Pretoria, South Africa, 18–20 June 2014. [Google Scholar]
- Berg, A. Detection and Tracking in Thermal Infrared Imagery; Linköping University Electronic Press: Linköping, Sweden, 2016. [Google Scholar]
- Nikulin, A.; de Smet, T.; Baur, J.; Frazer, W.; Abramowitz, J. Detection and identification of remnant PFM-1 ‘Butterfly Mines’ with a UAV-Based thermal-imaging protocol. Remote Sens. 2018, 10, 1672. [Google Scholar] [CrossRef] [Green Version]
- Smirnov, A.; Nikulin, A. Long-Range and tethered UAVs in UXO detection 2019, long-range and tethered UAVs in UXO detection, presentation. In Proceedings of the 7th Mine Action Technology Workshop, GCIHD, Basel, Switzerland, 7–8 November 2019. [Google Scholar]
- Bajic, M. Testing of detectors for non-explosive components of the IED, the non-linear junction, and the control line-wire 2017. In “Synergistic Technologies to Defeat Improvised Threat,” Proceedings of the 3rd C-IED Technology Workshop; Madrid, Spain, 24–26 October 2017, C-IED Centre of Excellence: Madrid, Spain, 2017. [Google Scholar]
- Bajić, M. Propagation model of harmonic radar for detection of nonlinear contacts of improvised explosive device. Polytech. Des. 2017, 210–218. [Google Scholar] [CrossRef]
- Šipoš, D.; Gleich, D.; Malajner, M. Stepped frequency radar for landmine detection attached to hexacopter. Presentation and paper. In Book of Papers, Proceedings of the 16th International Symposium MINE ACTION; Dubrovnik, Croatia, 10 April 2019, HCR Center for testing, development and training: Dubrovnik, Croatia, 2019. [Google Scholar]
- Šipoš, D.; Gleich, D. A Lightweight and low-power UAV-Borne ground penetrating radar design for landmine detection. Sensors 2020, 20, 2234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mayr, W. FindMine UAV im humanitären einsatz presentation, Urs Endress Foundation. In Proceedings of the 7th Mine Action Technology Workshop, GCIHD, Basel, Switzerland, 7–8 November 2019. [Google Scholar]
- Fasano, G.; Renga, A.; Vetrella, A.R.; Ludeno, G.; Catapano, I.; Soldovieri, F. Proof of concept of Micro-UAV-Based radar imaging. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1316–1323. [Google Scholar]
- Targett, K. Amulet UAS with GPR. In Proceedings of the 7th Mine Action Technology Workshop, GCIHD, Basel, Switzerland, 7–8 November 2019. [Google Scholar]
- Guldin, D. Development and Tests of a UXO Survey Drone System 2019. In Book of Papers, Proceedings of the 16th International Symposium MINE ACTION, Dubrovnik, Croatia, 10 April 2019; HCR Center for testing, development and training: Dubrovnik, Croatia, 2019. [Google Scholar]
- Guldin, D. Development and Tests of a UXO Survey Drone System 2019. In Proceedings of the 7th Mine Action Technology Workshop, GCIHD, Basel, Switzerland, 7–8 November 2019. [Google Scholar]
- Krtalić, A.; Bajić, M.; Ivelja, T.; Racetin, I. The AIDSS Module for data acquisition in crisis situations and environmental protection. Sensors 2020, 20, 1267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makki, I.; Younes, R.; Francis, C.; Bianchi, T.; Zucchetti, M. A Survey of landmine detection using hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2017, 124, 40–53. [Google Scholar] [CrossRef]
- Makki, I. Hyperspectral Imaging for Landmine Detection. Ph.D. Thesis, Lebanese Univerity and Politecnico di Torino, Torino, Italy, 2017. [Google Scholar]
- Makki, I.; Younes, R.; Khodor, M.; Khoder, J.; Francis, C.; Bianchi, T.; Rizk, P.; Zucchetti, M. RBF Neural network for landmine detection in H yperspectral imaging. In Proceedings of the 2018 7th European Workshop on Visual Information Processing (EUVIP), Tampere, Finland, 26–28 November 2018; pp. 1–6. [Google Scholar]
- Aikio, M. Hyperspectral Prism-Grating-Prism Imaging Spectrograph; VTT Publications: Espoo, Finland, 2001. [Google Scholar]
- Bajić, M.; Ivelja, T.; Krtalić, A.; Tomić, M.; Vuletić, D. The Multisensor and Hyper spectral survey of the UXO around the exploded ammunition depot, of the land mines test site vegetation. In Proceedings of the 10th International Symposium HUDEM, HCR Center for Testing, Development and Training. Šibenik, Croatia, 27–30 April 2013; Volume 9206, pp. 91–96. [Google Scholar]
- Bajic, M.; Gold, H.; Pračić, Ž.; Vuletić, D. Airborne sampling of the reflectivity by the hyperspectral line scanner in a visible and near infrared wavelengths. In Proceedings of the 24th Symposium of the European Association of Remote Sensing Laboratories, Dubrovnik, Croatia, 15–27 May 2004; pp. 25–27. [Google Scholar]
- Bajić, M. Airborne hyperspectral surveillance of the ship-based oil pollution in Croatian part of the Adriatic sea. Geod. List 2012, 66, 77–100. [Google Scholar]
- Bajić, M.; Ivelja, T. Transfer of knowledge and technologies from mine action to counter improvised explosive devices (C-IED) domain. Polytech. Des. 2016, 4, 300–309. [Google Scholar]
- Miljković, V.; Gajski, D. Adaptation of industrial hyperspectral line scanner for archaeological applications. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 5, 343–345. [Google Scholar] [CrossRef]
- Krtalić, A.; Miljković, V.; Gajski, D.; Racetin, I. Spatial distortion assessments of a low-cost laboratory and field hyperspectral imaging system. Sensors 2019, 19, 4267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bajic, M. Impact of Mine polluted area characteristics on the suitability of the airborne multisensor mine field Detection—The case of Croatia. In Proceedings of the International Airborne Remote Sensing Conference and Exhibition, 4th/21st Canadian Symposium on Remote Sensing, Ottawa, ON, Canada, 21–24 June 1999. [Google Scholar]
- Yvinec, Y.; Bajić, M.; Dietrich, B.; Bloch, I.; Vanhuysse, S.; Wolff, E.; Willekens, J. Space and Airborne Mined Area Reduction Tools, SMART Project Final Report, V2.2, Classification: Public; European Commission IST-2000-25044; European Commission: Brussels, Belgium, 2005. [Google Scholar]
- Bajic, M.; Beckel, L.; Breejen, E.; Sahli, H.; Schrotmeier, D.; Upsal, M.; Varas, F.J. Airborne Minefield Area Reduction-ARC; European Commission Research Directorates General Project 2001–2003; IST-2000-25300; Information Society Technologies Programme: Brussels, Belgium, 2000. [Google Scholar]
- Donohue, J. Introductory Review of Target Discrimination Criteria; Final Report, 16 April 1991–31 December 1991; Phillips Laboratory Air Force Systems, Command Hanscom Air Force Base: Wilmington, MA, USA, 1991. [Google Scholar]
- Agarwal, S. Modeling and Performance Estimation for Airborne Minefield Detection System. Master’s Thesis, University of Missouri-Rolla, Rolla, MO, USA, 2008. [Google Scholar]
- Lerner, W.D. Predicting the Emplacement of Improvised Explosive Devices: An Innovative Solution. Ph.D. Thesis, Capitol College, Laurel, MD, USA, April 2013. [Google Scholar]
- Johnson, D.; Ali, A. Modeling and simulation of landmine and improvised explosive device detection with multiple loops. J. Def. Model. Simul. Appl. Methodol. Technol. 2015, 12, 257–271. [Google Scholar] [CrossRef]
- Rajagopal, A.; Agarwal, S.; Ramakrishnan, S. Simulation-Based performance modeling for war fighter in loop minefield detection system. In Proceedings of the Winter Simulation Conference, New York, NY, USA, 4–7 December 2005; pp. 1160–1169. [Google Scholar]
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Manolakis, D.G. Taxonomy of detection algorithms for hyperspectral imaging applications. Opt. Eng. 2005, 44, 066403. [Google Scholar] [CrossRef]
- Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral image processing for automatic target detection applications. Linc. Lab. J. 2003, 14, 79–116. [Google Scholar]
- Matteoli, S.; Diani, M.; Corsini, G. A tutorial overview of anomaly detection in hyperspectral images. IEEE Aerosp. Electron. Syst. Mag. 2010, 25, 5–28. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, C. Hyperspectral Image Processing; Springer: Berlin, Germany, 2015; ISBN 978-7-118-08646-1. [Google Scholar]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The Spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Basener, W.F.; Nance, E.; Kerekes, J. The target implant method for predicting target difficulty and detector performance in hyperspectral imagery. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVII, SPIE, Orlando, FL, USA, 13 May 2011; p. 80481H. [Google Scholar]
- Evans, M.; Hastings, N.; Peacock, B. Statistical Distributions, 3rd ed.; Wiley: Hoboken, NJ, USA, 2000; pp. 31–33. [Google Scholar]
- Simonson, K.M. Statistical Considerations in Designing Tests of Mine Detection Systems: I-Measures Related to the Probability of Detection; Sandia National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 1998. [Google Scholar]
- Vollset, S.E. Confidence intervals for a binomial proportion. Stat. Med. 1993, 12, 809–824. [Google Scholar] [CrossRef] [PubMed]
- Abramowitz, J. MATLAB. Available online: https://www.mathworks.com/help/stats/betainv.html (accessed on 9 January 2021).




























| No | Action | Description |
|---|---|---|
| 1 | Correcting the geometry of measured target data by NN interpolation. | Use raw measured data of the target Figure 4a. Corrected targets are shown in Figure 4b and Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. ENVI |
| 2 | Extracting the target from its nearest environment | ENVI. |
| 3 | Decrease the extracted target (small target) to 0.05058 of its original dimensions. | ENVI: After decreasing dimension, export to the stack tifs. Match target pixels (0.945 mm) to pixels (18.681 cm) of terrain field (Figure 21b). |
| 4 | Export hyperspectral terrain field spectral data; 1000 × 1000 × 90, in 32-bit tiff stack. Co-ordinates can be pixel numbers or meters (if georeferenced). | Figure 18 (scene 147) and Figure 19 (scene 227). If desired scenes should be georeferenced, co-ordinates of pixels (in m) can be used. We recommend applying pixel co-ordinates and doing the georeferencing (if needed) on the simulation outcomes. |
| 5 | Implanting small targets in a blackboard stack (1000 × 1000 × 90), where blackboard pixels have value = 0; format 32 bits tiff. | Figure 22a. The targets are visible on the black background. ImageJ. |
| 6 | Inversing blackboard of step 5. Change targets area values to 1, and the values of the blackboard to 0, all in 32 bits floating-point format, in 90 channels. | This can be seen by inversing Figure 22b. ImageJ. |
| 7 | Implant areas of inversed small targets in blackboard stack of 1000 × 1000 × 90. | Figure 22b. ImageJ. |
| 8 | Locations of small targets into the scene of terrain | Figure 22c. Multiplying Figure 22b with the scene of the terrain in Figure 19. ImageJ. |
| 9 | Implanting small targets onto the scene of the terrain | Add blackboard array (Figure 22a) to the outcome of step 8. Result shown in Figure 22d. |
| Target | Samples per Band in the Measured Target | Samples per Band in the Decreased Target | Percentage % of Implanted Spectral Samples | Target Area m2 |
|---|---|---|---|---|
| Artillery shell | 45,661 | 108 | 0.2365 | 0.037690 |
| Bullet | 36,243 | 87 | 0.2400 | 0.030362 |
| Cluster munition | 24,653 | 63 | 0.2555 | 0.021986 |
| Mortar mine | 45,285 | 116 | 0.2562 | 0.040482 |
| UXOX | 19,251 | 52 | 0.2701 | 0.018147 |
| Landmine PMR2A | 7 | 1 | 14.2857 | 0.009500 |
| Landmine TMA-4 | 8 | 1 | 12.5000 | 0.063340 |
| Polynomial Approximation | |
|---|---|
| ASR 147 | |
| PODupper | y = 4E6x6 − 3E6x5 + 1E6x4 − 166833x3 + 14875x2 − 663.1x + 11.849 |
| POD | y = −4E6x6 + 2E6x5 − 240255x4 − 662.15x3 + 2877.7x2 − 220.25x + 5.0015 |
| PODlower | y = −9E6x6 + 6E6x5 − 1E6x4 + 177823x3 − 11922x2 + 400.99x − 5.2922 |
| BR 147 | |
| PODupper | y = 6E6x6 − 4E6x5 + 940755x4 − 131459x3 + 10406x2 − 429.58x + 7.4796 |
| POD | y = 1E7x6 − 7E6x5 + 2E6x4 − 199237x3 + 14057x2 − 526.59x + 8.1301 |
| PODlower | y = 1E7x6 − 6E6x5 + 1E6x4 − 152510x3 + 9421.4x2 − 306.4x + 4.1181 |
| CMR 147 | |
| PODupper | y = 8E6x6 − 5E6x5 + 1E6x4 − 202551x3 + 15760x2 − 620.39x + 10.161 |
| POD | y = 1E7x6 − 7E6x5 + 2E6x4 − 303933x3 + 24386x2 − 990.91x + 16.095 |
| PODlower | y = 8E6x6 − 6E6x5 + 2E6x4 − 250338x3 + 20267x2 − 835.47x + 13.698 |
| MMR 147 | |
| PODupper | y = 806.5x3 − 319.41x2 + 42.148x − 0.8546 |
| POD | y = 217.42x3 − 141.66x2 + 29.343x − 0.9423 |
| PODlower | y = −403.37x3 + 89.372x2 + 2.0295x − 0.259 |
| UXOXR 147 | |
| PODupper | y = 19706x4 − 8375.7x3 + 1204.7x2 − 61.222x + 1.3705 |
| POD | y = 13569x4 − 6690.5x3 + 1123.3x2 − 65.845x + 1.3051 |
| PODlower | y = 1E7x6 − 7E6x5 + 2E6x4 − 226501x3 + 16046x2 − 599.6x + 9.1702 |
| Function | Polynomial Approximation |
|---|---|
| ASR 227 | |
| PODupper | y = 1E7x6 − 7E6x5 + 2E6x4 − 242706x3 + 18625x2 − 743.66x + 12.321 |
| POD | y = 1E7x6 − 7E6x5 + 2E6x4 − 227551x3 + 16594x2 − 637.76x + 10.023 |
| PODlower | y = 6E6x6 − 3E6x5 + 681375x4 − 70842x3 + 4006.8x2 − 119.2x + 1.4781 |
| BR 227 | |
| PODupper | y = −3E7x6 + 2E7x5 − 5E6x4 + 643587x3 − 45100x2 + 1633x − 23.579 |
| POD | y = −5E7x6 + 3E7x5 − 7E6x4 + 884396x3 − 62088x2 + 2252.8x − 33.03 |
| PODlower | y = −3E7x6 + 2E7x5 − 4E6x4 + 572692x3 − 40514x2 + 1480x − 21.823 |
| CMR 227 | |
| PODupper | y = 1E7x6 − 7E6x5 + 2E6x4 − 222440x3 + 16107x2 − 590.99x + 9.0346 |
| POD | y = −1E6x6 + 302964x5 + 37216x4 − 19070x3 + 2276.7x2 − 103.6x + 1.7106 |
| PODlower | y = −9E6x6 + 5E6x5 − 1E6x4 + 145792x3 − 9412.4x2 + 316.94x − 4.3969 |
| MMR 227 | |
| PODupper | y = −1E6x6 + 1E6x5 − 346262x4 + 57389x3 − 5092.5x2 + 241.73x − 4.1651 |
| POD | y = −3E6x6 + 3E6x5 − 997759x4 + 163684x3 − 14079x2 + 621.58x − 10.871 |
| PODlower | y = −4E6x6 + 4E6x5 − 1E6x4 + 188319x3 − 15692x2 + 663.92x − 11.22 |
| UXOXR 227 | |
| PODupper | y = 1E7x6 − 1E7x5 + 3E6x4 − 427371x3 + 34075x2 − 1388.2x + 22.829 |
| POD | y = 2E7x6 − 1E7x5 + 4E6x4 − 523864x3 + 40335x2 − 1605.7x + 25.685 |
| PODlower | y = 1E7x6 − 8E6x5 + 2E6x4 − 269836x3 + 19689x2 − 755.96x + 11.847 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bajić, M., Jr.; Bajić, M. Modeling and Simulation of Very High Spatial Resolution UXOs and Landmines in a Hyperspectral Scene for UAV Survey. Remote Sens. 2021, 13, 837. https://doi.org/10.3390/rs13050837
Bajić M Jr., Bajić M. Modeling and Simulation of Very High Spatial Resolution UXOs and Landmines in a Hyperspectral Scene for UAV Survey. Remote Sensing. 2021; 13(5):837. https://doi.org/10.3390/rs13050837
Chicago/Turabian StyleBajić, Milan, Jr., and Milan Bajić. 2021. "Modeling and Simulation of Very High Spatial Resolution UXOs and Landmines in a Hyperspectral Scene for UAV Survey" Remote Sensing 13, no. 5: 837. https://doi.org/10.3390/rs13050837
APA StyleBajić, M., Jr., & Bajić, M. (2021). Modeling and Simulation of Very High Spatial Resolution UXOs and Landmines in a Hyperspectral Scene for UAV Survey. Remote Sensing, 13(5), 837. https://doi.org/10.3390/rs13050837