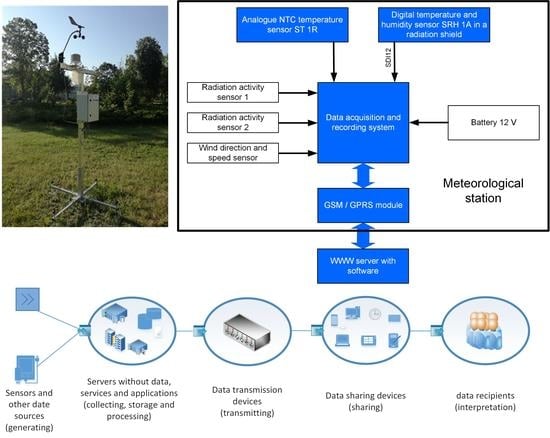
The Analysis and Modelling of the Quality of Information Acquired from Weather Station Sensors
Abstract
:1. Introduction
- publications on analyses of data obtained from sensors and their correctness,
- publications on the quality of information obtained from sensors used in meteorological stations,
- publications on the estimation of missing data in meteorological information,
- publications on the quality assessment of weather information.
2. Uncertainty Modelling Applied to Estimate the Quality of Information Obtained from Sensors of a Meteorological Station
2.1. Information Quality
- Availability (Dav)—a dimension that defines the possibility of using an information and communication technologies (ICT) element on demand, at a given time, and by an authorized process. This dimension is directly related to information security.
- Appropriate amount of data (Daad)—a dimension that determines how much data are adequate to complete the task while indicating that the amount is sufficient and more data could reduce information quality.
- Believability (Dbel)—a dimension which determines the degree to which information reflects reality. It may also be related to the credibility of the information source itself.
- Completeness (Dcom)—a dimension that determines whether the data are sufficient to perform a specific task.
- Concise representation (Dccr)—a dimension that determines the degree to which data are represented.
- Consistent representation (Dcsr)—a dimension that specifies to what extent data are represented in the same format.
- Ease of manipulation (Deom)—a dimension that determines how easily these data can be processed when applied to other tasks.
- Free of error (Dfoe)—the dimension that determines the extent to which the data are error-free.
- Interpretability (Dinter)—a dimension that defines the extent to which data are clear and represented in appropriate languages and symbols.
- Objectivity (Dobj)—the dimension which determines to what extent data are not subjective.
- Relevancy (Drelev)—a dimension that determines the usefulness of data in performing a specific task.
- Reputation (Dreput)—a dimension that determines the extent to which data are assessed in terms of its sources and content.
- Security (Dsec)—a dimension that determines the access limits to data to isolate them from unauthorized access.
- Timeliness (Dtim)—the dimension that determines the extent to which data are available on time to complete a task.
- Understandability (Duns)—a dimension that determines the understandability of data.
- Value-added (Dvadd)—a dimension that determines the benefits of using data and whether they themselves are beneficial to the task.
- m—the number of dimensions, information quality components (equals 16 according to the number of the above dimensions),
- w—a variable that determines the impact of a given dimension (i.e., a value in the range <0.1>).
2.2. Modelling Certainty Factor of Hypothesis
- CF—certainty factor,
- MB—knowledge mapping, i.e., measure of belief,
- MD—hypothesis based on some information.
- P—probability,
- s—hypothesis based on some information.
2.2.1. Parallel basic model
2.2.2. Serial basic model
2.3. Parallel-Serial Model of the Analysed Solution of the Meteorological Station
- Dimensions related to the main data source. In this case, the data source is the weather station. The dimensions associated with this source influence the value of the indirect hypothesis h1. In the case of data source redundancy, the h1 hypothesis consists of many indirect hypotheses.
- Dimensions related to collecting, storing, and processing of data. In this case, it is a computer system dedicated to performing specific tasks. The dimensions related to this state of information influence the value of the indirect hypothesis h2.
- Dimensions related to data transmission. This group includes devices for data transport and transmission. Data transport factors influence the value of the indirect hypothesis h3.
- Dimensions related to data sharing systems. This group includes imaging and sound devices transmitting data for interpretation as well as interfaces if the interpreter is a computer system, e.g., artificial intelligence (AI). The dimensions related to this state of information influence the value of the indirect hypothesis h4.
- Dimensions related to data interpretation. This group includes people and—as in this case –computer systems, e.g., AI. The dimensions related to this state of information influence the value of the indirect hypothesis h5.
- h1a—Basic data source provides valid data. Based on the observations of e1a.
- h1b—Auxiliary data source provides valid data. Based on observations from e1b.
- h1—The weather station delivers valid data. Based on observations of e1a and e1b.
- h2—Data collection, storage, and processing work properly. Based on the observations of e2.
- h3—Data transport systems work properly. Based on observations from e3.
- h4—Data sharing systems work properly and share data in the correct way. Based on the observations of e4.
- h5—Data are interpreted correctly. Based on observations e5.
- e1a.1—The detector is working properly.
- e1a.2—Detector failure.
- e1a.3—Lack of power.
- e1b.1—The detector is working properly.
- e1b.2—Detector failure.
- e1b.3—Lack of power.
- e2.1—Data collection, storage, and processing work properly.
- e2.2—Interruption of data transmission.
- e2.3—Data are not collected (e.g., lack of resources).
- e2.4—The data are not processed (e.g., insufficient capacity of the data processing system).
- e3.1—Data transport systems are working properly.
- e3.2—Link failure.
- e4.1—Data sharing systems are working properly and sharing data in the correct way.
- e4.3—Defective data sharing methods.
- e5.1—Data are interpreted correctly.
- e5.2—Badly trained staff (e.g., does not understand the message).
- e5.3—Incorrect data response of the interpreter.
3. Method Verification and its Computer Exemplification
- Digital temperature and relative humidity sensor marked with the catalogue symbol SRH1A (abbreviation comes from the words: sensor, relative humidity) placed in an anti-radiation shield.
- Analogue temperature sensor with negative temperature coefficient (NTC) thermistor marked with the catalogue symbol ST1R (abbreviation comes from words: sensor, temperature) placed in an anti-radiation shield.
- Wind speed and direction sensor.
- Two independent solar radiation intensity sensors.
- Operation temperature range −50 …+70 °C,
- Measurement accuracy ±0.5 °C,
- Measurement element 100 kΩ NTC,
- Sensor’s dimensions ø6 × 60 mm,
- Level of security IP 67.
- e1a—these are observations related to an analogue temperature sensor with a cable connection,
- e1b—these are observations related to a digital temperature sensor with a cable connection,
- e2—these are observations related to the system for data acquisition and recording with an input expansion card and a memory card,
- e3—these are observations related to the digital cellular communication module.
- e1a.1—the sensors work correctly, the observation coefficient is 0.95,
- e1a.2—faulty analogue sensor or broken signal wire, observation coefficient is 0.02 based on observations, data from the manufacturer, and wiring reliability analysis,
- e1a.3—battery voltage supply below 11 V or interrupted power line, the observation coefficient is 0.04 based on observation of the facility exploitation.
- e1b.1—the sensor and the SDI-12 link work correctly, the observation factor is 0.99,
- e1b.2—faulty sensor or serial data transmission error, the observation coefficient is 0.01 determined on the basis of observations and data from the manufacturer,
- e1b.3—battery voltage supply below 4 V or interrupted power line, the observation coefficient is 0.002 based on observation of the facility exploitation.
- e2.1—the recorder is working correctly, the observation coefficient is 0.99,
- e2.2—faulty microcontroller or expansion modules, the observation factor is 0.005 determined on the basis of observations and data from the manufacturer,
- e2.3—data archiving not possible due to overflow or memory card fault, the observation factor is 0.004 determined on the basis of observations and data from the manufacturer
- e2.4—battery supply voltage below 5 V or power line interruption, the observation factor is 0.002 based on the observation of the facility exploitation.
4. Simulation and Results using Real Measurements
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dorman, C.E. Early and Recent Observational Techniques for Fog. In Marine Fog: Challenges and Advancements in Observations, Modeling, and Forecasting; Koračin, D., Dorman, C., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Ilčev, S.D. Meteorological Ground Stations. In Global Satellite Meteorological Observation (GSMO) Applications; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Olchowik, W. Simulation of systems with solar collectors in relation to the raw meteorological data. Bull. Mil. Univ. Technol. 2017, 66, 37–54. [Google Scholar] [CrossRef]
- Sarkar, I.; Pal, B.; Datta, A.; Roy, S. Wi-Fi-Based Portable Weather Station for Monitoring Temperature, Relative Humidity, Pressure, Precipitation, Wind Speed, and Direction. In Information and Communication Technology for Sustainable Development; Tuba, M., Akashe, S., Joshi, A., Eds.; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Sugiarto, B.; Sustika, R. Data classification for air quality on wireless sensor network monitoring system using decision tree algorithm. In Proceedings of the 2nd International Conference on Science and Technology-Computer (ICST), Yogyakarta, Indonesia, 27–28 October 2016; pp. 172–176. [Google Scholar] [CrossRef]
- Płanda, B.; Skorupski, J. Methods of air traffic management in the airport area including the environmental factor. Int. J. Sustain. Transp. 2017, 11, 295–307. [Google Scholar] [CrossRef]
- Jaeger, A. Weather Hazard. Warning Application in Car-to-X Communication; Springer: Wiesbaden, Germany, 2016. [Google Scholar] [CrossRef]
- Ryguła, A.; Brzozowski, K.; Konior, A. Utility of Information from Road Weather Stations in Intelligent Transport Systems Application. In Tools of Transport Telematics; TST 2015; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Boulanger, J.; Aizpuru, J.; Leggieri, L.; Marino, M. A procedure for automated quality control and homogenization of historical daily temperature and precipitation data (APACH): Part 1: Quality control and application to the Argentine weather service stations. Clim. Change 2010, 98, 471–491. [Google Scholar] [CrossRef]
- Li, X.; Zou, D.; Feng, W.; Xie, W.; Shi, L. Study of Quality Control Methods for Moored Buoys Observation Data. In Proceedings of the International Conference on Meteorology Observations (ICMO), Chengdu, China, 28–31 December 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Qu, S.; Feng, Y.; Li, T. Comparative Study on the Reliability of Weather Radar Intensity Data. In Proceedings of the International Conference on Meteorology Observations (ICMO), Chengdu, China, 28–31 December 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Vas, Á.; Tóth, L. Investigation of a Hybrid Sensor- and Computational Network for Numerical Weather Prediction Calculations. In Distributed Computer and Communication Networks; DCCN 2019; Vishnevskiy, V., Samouylov, K., Kozyrev, D., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Hema, N.; Kant, K. Reconstructing missing hourly real-time precipitation data using a novel intermittent sliding window period technique for automatic weather station data. J. Meteorol Res. 2017, 31, 774–790. [Google Scholar] [CrossRef]
- Rosillon, D.; Huart, J.P.; Goossens, T.; Journée, M.; Planchon, V. The Agromet Project: A Virtual Weather Station Network for Agricultural Decision Support Systems in Wallonia, South of Belgium. In Ad-Hoc, Mobile, and Wireless Networks; ADHOC-NOW 2019; Palattella, M., Scanzio, S., Coleri Ergen, S., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Juneja, A.; Das, N. Big Data Quality Framework: Pre-Processing Data in Weather Monitoring Application. In Proceedings of the International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 559–563. [Google Scholar] [CrossRef]
- Sattar, F.; Karray, F.; Kamel, M.; Nassar, L.; Golestan, K. Recent Advances on Context-Awareness and Data/Information Fusion in ITS. Int. J. Intell. Transp. Syst. Res. 2016, 14, 1–19. [Google Scholar] [CrossRef]
- Schubert, R.; Obst, M. The Role of Multisensor Environmental Perception for Automated Driving. In Automated Driving; Watzenig, D., Horn, M., Eds.; Springer: Cham, Switzerland, 2017; pp. 161–182. [Google Scholar] [CrossRef]
- Penenko, V.V.; Tsvetova, E.A.; Penenko, A.V. Methods based on the joint use of models and observational data in the framework of variational approach to forecasting weather and atmospheric composition quality. Russ. Meteorol. Hydrol. 2015, 40, 365–373. [Google Scholar] [CrossRef]
- Wei, C.-C.; Hsu, C.-C. Extreme Gradient Boosting Model for Rain Retrieval using Radar Reflectivity from Various Elevation Angles. Remote Sens. 2020, 12, 2203. [Google Scholar] [CrossRef]
- Tang, G.; Long, D.; Behrangi, A.; Wang, C.; Hong, Y. Exploring deep neural networks to retrieve rain and snow in high latitudes using multisensor and reanalysis data. Water Resour. Res. 2018, 54, 8253–8278. [Google Scholar] [CrossRef] [Green Version]
- International Organization for Standardization. Data Quality—Part 8: Information and Data Quality: Concepts and Measuring; ISO/IEC 8000-8:2015; ISO: Geneva, Switzerland, 2015. [Google Scholar]
- International Organization for Standardization. Quality Management Systems—Fundamentals and Vocabulary; ISO/IEC 9000:2015; ISO: Geneva, Switzerland, 2015. [Google Scholar]
- International Organization for Standardization. Quality Management Systems—Requirements; ISO/IEC 9001:2015; ISO: Geneva, Switzerland, 2015. [Google Scholar]
- Massachusetts Institute of Technology Information Quality (MITIQ) Program. Available online: http://mitiq.mit.edu (accessed on 2 May 2020).
- Fisher, C.; Lauria, E.; Chengalur-Smith, S.; Wang, R. Introduction to Information Quality; Authorhouse: Bloomington, IN, USA, 2011. [Google Scholar]
- Wang, R.Y.; Pierce, E.M.; Madnick, S.; Fisher, C.W. (Eds.) Information Quality. Advances in Management Information Systems; M.E. Sharpe: Armonk, NY, USA, 2005. [Google Scholar]
- Dempster, A.P. Upper and Lower Probabilities Inducted by a Multi-valued Mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Krzykowska, K.; Krzykowski, M. Forecasting Parameters of Satellite Navigation Signal through Artificial Neural Networks for the Purpose of Civil Aviation. Int. J. Aerosp. Eng. 2019, 1, 1–11. [Google Scholar] [CrossRef]
- Mazur, M. Qualitative Information Theory; Scientific and Technical Publishers: Warsaw, Poland, 1970. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NY, USA, 1976. [Google Scholar]
- Heckerman, D. The certainty-factor model. In Encyclopedia of Artificial Intelligence; Shapiro, S., Ed.; Wiley: New York, NY, USA, 1992; pp. 131–138. [Google Scholar]
- Shortliffe, E.H.; Buchanan, B.G. Rule-Based Expert Systems: The MYCIN Experiments of the Stanford Heuristic Programming Project; Addison-Wesley Publishing Co. Inc.: Boston, MA, USA, 1984. [Google Scholar]
- Oleński, J. Economics of Information. The Basics; Polish Economic Publishing House: Warsaw, Poland, 2001. [Google Scholar]
- Rychlicki, M.; Kasprzyk, Z.; Rosiński, A. Analysis of Accuracy and Reliability of Different Types of GPS Receivers. Sensors 2020, 20, 6498. [Google Scholar] [CrossRef]
- Jacyna, M.; Żak, J.; Gołębiowski, P. The EMITRANSYS model and the possibilities of its application for the analysis of the development of sustainable transport systems. Combust. Engines 2019, 179, 243–248. [Google Scholar] [CrossRef]
- Jurczyk, A.; Szturc, J.; Otop, I.; Ośródka, K.; Struzik, P. Quality-Based Combination of Multi-Source Precipitation Data. Remote Sens. 2020, 12, 1709. [Google Scholar] [CrossRef]
- Siergiejczyk, M.; Krzykowska, K.; Rosiński, A. Evaluation of the influence of atmospheric conditions on the quality of satellite signal. In Marine Navigation; Weintrit, A., Ed.; CRC Press/Balkema: London, UK, 2017; pp. 121–128. [Google Scholar] [CrossRef]
- Bednarek, M.; Dąbrowski, T.; Olchowik, W. Selected practical aspects of communication diagnosis in the industrial network. J. KONBiN 2019, 49, 383–404. [Google Scholar] [CrossRef] [Green Version]
- Dudek, E.; Kozłowski, M. Analysis of aeronautical information potential incompatibility—Case study. J. KONBiN 2017, 41, 59–82. [Google Scholar] [CrossRef] [Green Version]
- Stawowy, M. Method of Multilayer Modeling of Uncertainty in Estimating the Information Quality of ICT Systems in Transport; Publishing House of Warsaw University of Technology: Warsaw, Poland, 2019. [Google Scholar]
- Baggini, A. (Ed.) Handbook of Power Quality; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Watral, Z.; Michalski, A. Selected Problems of Power Sources for Wireless Sensors Networks. IEEE Instrum. Meas. Mag. 2013, 16, 37–43. [Google Scholar] [CrossRef]
- Michalski, A.; Watral, Z.; Jakubowski, J. Energy Harvesting—A real possibility of alternative power supply to wireless sensor networks. In Selected Aspects of the Use of “Energy Harvesting” Technology in Supplying Wireless Sensor Networks; Military Academy of Technology: Warsaw, Poland, 2017; pp. 39–88. [Google Scholar]
- Paś, J.; Rosiński, A.; Chrzan, M.; Białek, K. Reliability-Operational Analysis of the LED Lighting Module Including Electromagnetic Interference. IEEE Trans. Electromagn. Compat. 2020, 62, 2747–2758. [Google Scholar] [CrossRef]
- Paś, J.; Rosiński, A.; Szulim, M.; Łukasiak, J. Modelling the Safety Levels of ICT Equipment Exposed to Strong Electromagnetic Pulses. In Proceedings of the 14th International Conference on Dependability of Computer Systems DepCoS-RELCOMEX 2019, Brunów, Poland, 1–5 July 2019; Zamojski, W., Mazurkiewicz, J., Sugier, J., Walkowiak, T., Kacprzyk, J., Eds.; Springer: Cham, Switzerland, 2020; pp. 393–401. [Google Scholar] [CrossRef]
- Stawowy, M.; Perlicki, K.; Sumiła, M. Comparison of Uncertainty Multilevel Models to Ensure ITS Services. In Safety and Reliability: Theory and Applications. In Proceedings of the European Safety and Reliability Conference ESREL 2017, Portoroz, Slovenia, 18–22 June 2017; Cepin, M., Bris, R., Eds.; CRC Press/Balkema: London, UK, 2017; pp. 2647–2652. [Google Scholar] [CrossRef]
- Humidity and Temperature Sensor SRH1A. Available online: http://www.pmecology.com/pl/wp-content/uploads/2019/09/RH_TEMP-Sensor-PM-Ecology_spec.pdf (accessed on 5 March 2020).
- Temperature Sensor. Available online: https://www.pmecology.com/wp-content/uploads/2018/08/Temperature-sensor-ST1R-PM-Ecology_spec.pdf (accessed on 5 March 2020).
- Będkowski, L.; Dąbrowski, T. Basics of Maintenance, Vol. II Basic of Operational Reliability; Military University of Technology: Warsaw, Poland, 2006. [Google Scholar]
- Klimczak, T.; Paś, J. Basics of Exploitation of Fire Alarm Systems in Transport Facilities; Military University of Technology: Warsaw, Poland, 2020. [Google Scholar]
- Duer, S.; Duer, R.; Mazuru, S. Determination of the expert knowledge base on the basis of a functional and diagnostic analysis of a technical object. Rom. Assoc. Nonconv. Technol. 2016, 2, 23–29. [Google Scholar]
- Grabski, F. Semi-Markov Processes: Applications in System Reliability and Maintenance; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]















| Parameter | Relative Humidity (RH) Measurement | Temperature Measurement |
|---|---|---|
| Measurement range | 0 … 100%RH | −40 … +70 °C |
| Accuracy at 25 °C | ±1.8%RH (0 … 90%RH) ±3.0%RH (>90%RH) | ±0.3 °C (0 … 70 °C), ±0.5 °C for the remaining values |
| Nonlinearity | <0.1%RH | - |
| Long-term stability | <0.25%RH/year | <0.02 °C/year |
| Measurement resolution | 0.01%RH | 0.01 °C |
| e1a | e1b | e2 | e3 | e4 | e5 | |
|---|---|---|---|---|---|---|
| 1. | 0.95 | 0.99 | 0.99 | 0.892 | 0.865 | 0.781 |
| 2. | −0.02 | −0.01 | −0.005 | −0.122 | −0.152 | −0.185 |
| 3. | −0.04 | −0.002 | −0.004 | −0.03 | −0.114 | −0.251 |
| 4. | −0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stawowy, M.; Olchowik, W.; Rosiński, A.; Dąbrowski, T. The Analysis and Modelling of the Quality of Information Acquired from Weather Station Sensors. Remote Sens. 2021, 13, 693. https://doi.org/10.3390/rs13040693
Stawowy M, Olchowik W, Rosiński A, Dąbrowski T. The Analysis and Modelling of the Quality of Information Acquired from Weather Station Sensors. Remote Sensing. 2021; 13(4):693. https://doi.org/10.3390/rs13040693
Chicago/Turabian StyleStawowy, Marek, Wiktor Olchowik, Adam Rosiński, and Tadeusz Dąbrowski. 2021. "The Analysis and Modelling of the Quality of Information Acquired from Weather Station Sensors" Remote Sensing 13, no. 4: 693. https://doi.org/10.3390/rs13040693
APA StyleStawowy, M., Olchowik, W., Rosiński, A., & Dąbrowski, T. (2021). The Analysis and Modelling of the Quality of Information Acquired from Weather Station Sensors. Remote Sensing, 13(4), 693. https://doi.org/10.3390/rs13040693