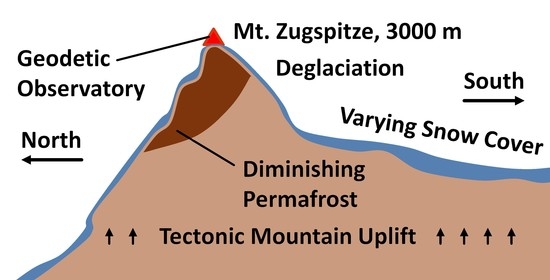
Geodetic-Gravimetric Monitoring of Mountain Uplift and Hydrological Variations at Zugspitze and Wank Mountains (Bavarian Alps, Germany)

Abstract

In 2004, first absolute gravity (AG) measurements were performed on the top of Mt. Zugspitze (2 sites) and at the foot (1 site) and top (1 site) of Mt. Wank. Mt. Wank (summit height 1780 m) and Mt. Zugspitze (2960 m) are about 15 km apart from each other and belong geologically to different parts of the Northern Limestone Alps. Bridging a time span of 15 years, the deduced gravity variations for Zugspitze are in the order of −0.30 μm/s² with a standard uncertainty of 0.04 μm/s². The Wank stations (foot and top) show no significant gravity variation. The vertical stability of Wank summit is also confirmed by results of continuous GNSS recordings. Because an Alpine mountain uplift of 1 or 2 mm/yr cannot explain the obtained gravity decline at Zugspitze, the dominating geophysical contributions are assumed to be due to the diminishing glaciers in the vicinity. The modelled gravity trend caused by glacier retreat between epochs 1999 and 2018 amounts to −0.012 μm/s²/yr at both Zugspitze AG sites. This explains more than half of the observed gravity decrease. Long-term variations on inter-annual and climate-relevant decadal scale will be investigated in the future using as supplement superconducting gravimetry (installed in 2019) and GNSS equipment (since 2018).

1. Introduction

With a height of almost 3000 m above sea level Mt. Zugspitze in southern Germany is the country’s highest mountain. Due to its touristic infrastructure, it is an ideal location for geodynamic research to study the long-term uplift of the Alpine orogeny, which started in the late Cretaceous and is still an active mountain building process [1]. In addition to the tectonic uplift caused by the collision of the Eurasian and African lithospheric plates, a secular uplift is superimposed due to the crustal viscoelastic rebound since the deglaciation after the last glacial maximum (LGM). E.g. in [2], it is supposed that ≈90% of the geodetically measured rock uplift in the Alps is explainable by the Earth’s viscoelastic response to LGM deglaciation. Therein, postglacial isostatic adjustment and erosional unloading are compared with geodetic measurements, which are presented in [3] and are obtained from precise levelling in Austria performed over a time span of more than 60 years. In the western part of Austria along the alpine main ridge, uplift rates of 1 to 2 mm/yr have been derived from these geometric levellings. The Austrian levelling lines also surround the area of Mt. Zugspitze which is part of the Wetterstein Mountains (Northern Limestone Alps). According to the map published by [3] there is an uplift rate of about 1.5 mm/yr in this region. [4] analyzed more than 12 years of GNSS data and derived an ongoing average vertical rate of 1.8 mm/yr for the main mountain ridge of the Alps. At several places in the central area of the Western Alps, in the Swiss Alps, and in the Southern Alps they observe fastest uplift rates of more than 2 mm/yr. The uplift decreases towards the margins of the mountains to rates between 0.0 and 0.5 mm/yr. According to [4], the northern foreland basin of the Alps is not active.

In addition to the proposed explanation in [2], other ongoing processes like elastic deformation due to recent ice mass changes and decadal variations in the terrestrial water storage might also contribute to mountain uplift [5,6]. Uplift rates from present day glacier retreat in the Alps are estimated to be around 0.1–0.2 mm/yr in the whole Alpine belt with localized maxima of up to 0.9 mm/yr (Mount Blanc region) in areas of significant mass loss. For the northern rim of the Alps, uplift rates of 0.05–0.1 mm/yr are calculated. A continuation of geodetic and gravimetric observations with a best possible long-term stability will support investigations to understand the ongoing uplift processes.

The Zugspitze catchment offers an almost ideal infrastructure for hydrological and climate research with the Environmental Research Station Schneefernerhaus situated just 300 m below the summit and taking key meteorological measurements at several sites in the area [7,8]. The seasonal to inter-annual variability of the hydrological situation, particularly the change of snow cover in a warming climate has also been studied there, viewing the catchment as an accessible representative of processes in the entire Alps [9,10]. Also the diminishing permafrost in the north face of the summit has been monitored for over a decade.

The Bavarian Environmental Agency (Bayerisches Landesamt für Umwelt) reports that the increase of the mean temperature at Zugspitze of about 1.6 K during the past 100 years has reduced the permafrost in a borehole close to the peak from a total length of 34 m in 1915 to 24.5 m in 2015 [11]. It is projected that the increasing ambient temperature will lead to the disappearance of permafrost at Zugspitze in the second half of this century. In [12], the authors concluded from experiments that ice segregation in near-surface permafrost leads progressively to rock fracture and heave, whereas permafrost degradation leads episodically to melt of segregated ice and rock settlement.

For geodynamic as well as for hydrological research, the geodetic combination of ground-based gravimetric and geometric measurements is a promising way to monitor such variations and to support model predictions by observational data, see for example [13,14]. Gravity measurements are not only sensitive to height changes (distance change to Earth’s center of mass) but also to mass variabilities (e.g. water, soil moisture, permafrost and glacier ice variations). Applying gravimetric and geometric techniques enables discrimination between subsurface mass variations associated or not associated with vertical surface deformation. Therefore, absolute gravimetry, superconducting gravimetry and GNSS are complementary measuring techniques in geodesy, which is exploited in this paper, cf. [15].

2. Methodology and Observational Results

In this section, we explain absolute gravimetry supported by two other geodetic methods, GNSS and superconducting gravimetry, to monitor and investigate gravity variations in the Bavarian Alps. We explain how data of each geodetic method are collected, analyzed, and processed. The joint examination allows verification of results from long-term absolute gravimetry and will allow for a more complex interpretation in the future by demonstrating seasonal and inter-annual hydrological mass variations.

2.1. Absolute Gravimetry with the Hannover Free-Fall Gravimeter FG5 No. 220

In 2002, the University of Hannover (now Leibniz University Hannover, LUH) received the new absolute gravity meter FG5-220 from Micro-g Solutions, Inc. (Erie, CO, USA, cf. [16]). The commercial FG5 system is the succeeding generation of the JILA free-fall system which was developed at the University of Colorado Joint Institute of Laboratory Astrophysics [17]. In 2012, the Hannover gravimeter was upgraded to the X-version [18] benefitting from the optimizations w.r.t. instrumental vibrations (recoil compensation), less sensitivity to Coriolis force and the longer free-fall distance of the test mass. The free-fall length of the X-version is about 30 cm instead of 20 cm and the top point of the measuring segment along the vertical has changed to 138 cm (previously 128 cm) above floor level.

2.1.1. Long-Term Measuring Repeatability

In geoscientific research, the precise measurement of gravity variations and the determination of secular trends over years to many decades is a central aim. Observed gravity differences between two epochs should not be compromised by an instable measuring level of the absolute gravimeter. For example, the determination of the post glacial rebound in Fennoscandia [19] requires a gravimeter to be stable within 0.02 μm/s² over many years. Episodic comparisons with many qualified absolute gravimeters are performed to verify the instrumental stability or to determine a shift of the gravimeter’s measuring level. A rigorous control of the stability with respect to a ‘‘true’’ gravity value at the moment of an absolute gravity measurement is not feasible. The real g-value is not known with superior accuracy, and a ‘‘standard’’ absolute gravimeter, which is superior to the state-of-the-art FG5 meters, does not exist. In [20], it is described how the accuracy and the measuring stability of FG5-220 is controlled with reference to the SI units. The Hannover group demonstrated their capability in absolute gravimetry within a project to determine the Fennoscandian land-uplift characterized by small gravity rates between 0.00 and 0.02 μm/s² at the observation sites, see [19].

Table 1. Compilation of gravity discrepancies (with standard uncertainties Std.U) between the FG5-220 results and the comparison reference values (CRV). Several European Comparison of Absolute Gravimeters (ECAG) were performed in Walferdange (Wal.), Luxembourg, other comparisons were organized in Sévres (Sév.), France, Belval (Bel.), Luxembourg, and Wettzell (Wet.), Germany. The different CRVs solutions are presented by [23] for ECAG2003, [24] for ECAG2007, and by [25] for the others.

Comparisons	Site	Epoch	No. of Gravimeters	Δg [μm/s2] (FG5-220 − CRV)	Std.U of Δg [μm/s2]
ECAG2003	Wal.	November 2003	13	−0.019	0.028
ECAG2007	Wal.	November 2007	19	+0.024	0.022
CCM.G-K1	Sév.	October 2009	21	+0.006	0.021
EURAMET.M.G-K1	Wal.	November 2011	21	+0.014	0.020
CCM.G-K2	Wal.	November 2013	25	+0.018	0.019
EURAMET.M.G-K2	Bel.	October 2015	17	+0.038	0.021
EURAMET.M.G-K3	Wet.	April 2018	16	0.000	0.021

summarizes the results of FG5-220 obtained from international comparison campaigns. Since 2009, the comparisons are called “key comparisons” strictly following metrological standards. They are organized by the Consultative Committee for Mass and Related Quantities (CCM) and EURAMET, cf. [21,22].

Shortly after the comparison in 2003, an instrumental instability was detected and eliminated: the input beam fiber was only poorly attached to the interferometer base and started to loosen. Since the beginning of 2004, the absolute gravimeter FG5-220 is assumed to be in its optimal adjustment condition (from the operators’ point of view) and specific instrumental reasons for the varying Δg-values in Table 1 cannot be given. Overall, the deviations from the CRVs are consistent with the given uncertainty estimates Std.U, which are defined with a statistical level of confidence of 68.3% corresponding to the classical definition of the standard deviation (1-σ estimate). Thus, as conservative estimate for the long-term stability from 2004 to present, we state here an instrumental uncertainty of 0.02 μm/s². With the upgrade of the instrument to the X-version in 2012, the measuring level has not changed. This empirical estimate agrees with the derived precision of FG5-220 as presented in [19] where FG5-220 was compared with several other FG5 instruments participating in the Fennoscandian land-uplift project.

2.1.2. Measurement Procedure and Applied Gravity Reductions

For the reduction of local noise and other disturbances, a few thousand computer controlled drops (free-fall experiments) are performed per site. Generally, the measurements are subdivided into sets of 50 or 100 drops each (Δt_drop= 10 s, Δt_set = 30 or 60 min), and distributed over 1 to 3 days. A sequence of sets, which is automatically performed and started by pushing the run button of the PC, is called a run and spans a time period of, e.g., 12 h (one night). Its result is the average of all drops, reduced for gravity variations due to Earth’s body and ocean tides, polar motion, and atmospheric mass movements. Because the assembly of the gravimeter components and the careful arranging of the tripod feet on the non-perfect floor foundation cause a slight dependency of the g-result on each gravimeter setup, two or more setups with different orientations of the tripod feet are used for internal control. The final station result is the arithmetic mean of g-results from the different setups.

Within the vacuum chamber of the FG5 gravimeter, the free-fall path of the accelerating test mass along the plumb line has a length of up to 30 cm. Gravity is strongly height dependent which requires to determine the vertical gravity gradient by relative gravimetry along the plumb line above the ground mark of the absolute point. In the campaigns with the Hannover FG5-220 in the Bavarian Alps, the gradients were derived from gravity differences (Δg values) measured with a tripod at different heights above floor level (e.g., sensor heights at Zugspitze in 2004: h_down = 0.265 m and h_up = 1.311 m; in 2018: 0.218 m and 1.248 m; in 2019: 0.215 m and 1.593 m). After about 10 Δg measurements, the average gravity differences are obtained with a standard deviation of about 0.01 μm/s². In general, the height differences for the gradient determination are always close to 1 m, and the upper point is always close to the so-called effective instrumental height of the FG5 gravimeter (around 1.25 m), where the influence of any uncertainty of the gradient becomes almost zero [26,27]. Only in 2019, the upper height was chosen close to 1.6 m above floor level instead of 1.25 m. Combining the 2018 and 2019 relative measurements at the three height levels of around 0.2 m, 1.25 m and 1.60 m allows the determination of a quadratic component of the vertical gravity gradient. With this, an improved gradient (constant term) can be provided for the FG5’s free-fall distance above the ground mark which is between about 108 to 138 cm height.

The effective instrumental height for the mean g-result of a single run varies slightly with a new setup and depends on the installation of the gravimeter, the height of the floor mark above the surrounding floor level and on the used free-fall distance in the data processing. In 2004, the effective height of FG5-220 was about 1.22 m above floor mark, and in 2018 the height of the improved X-version was 1.26 m above floor mark. To avoid or minimize any deterioration of the results (g-values) caused by uncertainties of the vertical gradient, which is actually not a constant factor along the plumb line, the final absolute g-result is transferred to the reference height h_ref = 1.250 m for FG5-220, X-version, and to h_ref = 1.200 m for the original version of FG5-220. This ensures that the vertical gradient is applied to transfer the g-value over a small distance of a few centimeters only. In this way, the station time series (history) of the gravimeter point can be used best to investigate a secular gravity change over years to decades. If gravity determinations from different epochs and different instruments are referred to an identical reference height of a site, all g-results can directly be compared. A gravity value close to floor level supports the connection of relative gravimetric ties with absolute points. The sensor height of the used Hannover relative gravimeter Scintrex CG3M-4492 is about 0.26 m above floor level. Thus, a reference height of 0.260 m has been chosen for the relative connections.

The gravimetric effect of atmospheric mass variations on the absolute measurements were reduced using local barometric readings and applying the factor −3.0 nm/s² per hPa to the pressure differences compared to a standard atmosphere which is recommended in the IGRS Conventions 2020 [28].

Table A1. Applied Earth tide data set with amplitude factors and phase shifts observed at ZUGOG with superconducting gravimeter OSG#052. The tidal waves with periods longer than 1 month are considered with the general values 1.160 (Ampl. factor) and 0.000° (Phase lead). The parameter of the partial tides M4 and M5 are assumed to be caused by non-linear shallow water tides of unknown source. The amplitudes of the M4 and M5 body tides are almost zero which is why these tides do not have any significance for absolute gravimetry.

Frequency [cpd] [cpd]		Ampl.	Phase	Tide
Start	End	Factor	Lead [°]	Symbol
0.000000	0.000001	1.00000	0.0000	DC
0.000100	0.004107	1.16000	0.0000	Long
0.004108	0.020884	1.16000	0.0000	SSA
0.020885	0.054747	1.15470	7.5156	MM
0.054748	0.091348	1.09556	5.7125	MF
0.091349	0.122801	1.37233	−8.4336	MTM
0.122802	0.501369	0.93361	15.5671	MQM
0.501370	0.911390	1.14762	−0.2793	Q1
0.911391	0.947991	1.15066	0.0377	O1
0.947992	0.981854	1.14759	0.2371	NO1
0.981855	0.998631	1.15131	0.0423	P1
0.998632	1.001369	1.35650	22.1020	S1
1.001370	1.023622	1.13835	0.1450	K1
1.023623	1.035379	1.15820	1.1338	TET1
1.035380	1.057485	1.15392	0.2098	J1
1.057486	1.071833	1.12218	−0.0208	SO1
1.071834	1.470243	1.14903	0.3559	OO1
1.470244	1.880264	1.16169	2.2840	2N2
1.880265	1.914128	1.17266	2.0763	N2
1.914129	1.950419	1.18621	1.5197	M2
1.950420	1.984282	1.17365	2.6148	L2
1.984283	2.002736	1.18443	0.1055	S2
2.002737	2.451943	1.18732	0.4413	K2
2.451944	3.381378	1.07683	−0.1141	M3
3.381379	4.347615	0.06782	37.7596	M4
4.347616	7.000000	2.68314	125.1959	M5

in the Appendix A compiles the Earth tide parameters for the tidal reduction. These parameters have been determined from continuous recordings with the GWR superconducting gravimeter (SG) OSG#052 since 1st of January, 2019 (15 months length). For details on the OSG#052, see [15]. SGs are manufactured by GWR Instruments, Inc., San Diego. Overviews and information in great detail are given, e.g., by [29,30]. Applying the most precise SG tidal results, a complete re-processing of all absolute gravity observations at Mt. Zugspitze and Mt. Wank with the Hannover instrument has been conducted to improve the reduction of unwanted gravity effects. For a more detailed description of gravity reductions applied to FG5-220 measurements, refer to [31].

2.1.3. Absolute Gravimetric Measurements at Mt. Zugspitze and Mt. Wank since 2004

Four absolute gravity stations were occupied in 2004, with two of them at the top of Mt. Zugspitze, cf. [32,33]. They are close to the German town Garmisch-Partenkirchen, see Figure 1. The Wank stations are located in the cable car stations at the foot and at the top of the mountain with a height difference of about 1000 m. Mt. Wank belongs to the Ester Mountains which are a small mountain range in Bavaria. They are classified as part of Bavarian Prealps or of the larger chain of Northern Limestone Alps. Mt. Zugspitze is part of the Wetterstein Mountains (Northern Limestone Alps), is crossed by the German-Austrian border and has a peak height of 2960 m.

Due to technical demands in the Environmental Research Station Schneefernerhaus, the absolute point 200, see [32], was relocated to an adjacent place in 2011 (new point 202). This was possible with the help of a witness point nearby which was set up in 2004. In addition to the absolute point from 2004 in an old telecommunication building (Telekom) on the summit of Zugspitze, a second point in the Zugspitze Geodynamic Observatory Germany (ZUGOG, GFZ Potsdam, [15]) was established very close to the Telekom site in September 2018. ZUGOG is located in an oddly shaped building that will not allow any snow cover on its steep roof (Figure 2). Its aim is to investigate in detail climate-relevant hydrological processes by means of a continuous gravity record with high temporal resolution. Thus, the superconducting gravimeter (SG) OSG#052 and GNSS equipment was set up at ZUGOG operating since September 2018. Recurring absolute gravity observations are needed to determine the long-term drift of the OSG#052 record and its calibration. In the future, due to the new ZUGOG site, absolute gravity observations are no longer planned in the Telekom building. But it will still be a witness point. Figure 2 shows the top of Mt. Zugspitze with the facilities where the absolute gravity sites are located. The twin station configuration on Mt. Zugspitze (ZUGOG and Schneefernerhaus) supports relative gravimetry to control the calibration of relative instruments within this extreme environment regarding air pressure and gravity range. In addition, the two sites increase the reliability of absolute gravimetry on Mt. Zugspitze. The absolute observations on both sites should verify each other. All observation campaigns were carried out during the annual season with minimum snow coverage, which is from end of summer to autumn. This time window was chosen to avoid varying effects of snow masses in the gravimetric trend signal (aliasing) as best as possible.

Table 2. Coordinates (WGS1984) of the absolute gravity sites occupied by the Hannover FG5-220.

Station	Start	φ [°]	λ [°]	H [m NN]	Description
Wank Berg	2004	47.5072	11.1443	1738.03	Station of the Wank cable car (summit)
Wank Tal	2004	47.5041	11.1062	735.29	Station of the Wank cable car (foot)
Zugspitze Telekom	2004	47.4211	10.9851	2940.96	Telecom building at summit
Schneefernerhaus 200	2004	47.4164	10.9798	2659.81	Environmental Research Station Schneefernerhaus, point 200 destroyed
Schneefernerhaus 202	2011	47.4164	10.9798	2659	New point 202 adjacent to former 200
Zugspitze ZUGOG	2018	47.4207	10.9847	2938	Adjacent to the superconducting gravimeter OSG#052 in ZUGOG

provides the coordinates of the absolute gravity sites with the installation dates and a short description. The coordinates are used to apply reductions for tides and atmospheric mass redistribution. The site Schneefernerhaus 200 is no longer available. In 2004, the heights were determined within the national height network by levelling to available bench marks. Figure 3 shows the Hannover absolute gravimeter in the cable car station Wank Berg in 2019 (excellent place w.r.t. working space, supply of electrical power, light, temperature stability) and in ZUGOG in front of the superconducting gravimeter in 2018 (severe problems with stable temperature).

Illustratively, a depictive representation of the station determination at Wank Berg (2019) is given with Figure 4. This provides an overview of the quality of that station determination. The upper part shows the drop-to-drop scatter of two runs. The scatter looks homogeneous and small. Thus, the environmental conditions (noise by wind, running machines, traffic, etc.) were favourable. A small shift is visible between the first and second run. The two runs correspond to two gravimeter setups, one in south and one in north direction. The orientation of FG5-220 is simply defined by one of the tripod feet which has a spirit level attached to its top. Also the set-to-set scatter diagram (lower panel) reveals a clear bias between the two setups. The two runs were performed at night time which often helps to avoid man-made disturbances during the day or to avoid the impact of temperature variations on the adjustment of the gravimeter during a sunny day. The histogram in the middle part depicts the statistical distribution around the mean g-value of all drops and statistical quantities are given. The standard deviation of the mean value is small, below 1 nm/s², and the standard deviation of the scatter is close to the best precision, FG5-220 can provide (best: 20 to 30 nm/s²). More numerical details about the measurements at Wank Berg (2019) are given in

Table A2. Absolute gravity values of the FG5-220 measurements at the bottom and top of Mt. Wank (facilities of Bayerische Zugspitzbahn Bergbahn AG). The gradient insensitive sensor height depends on the gravimeter setup and is about 1.25 m above floor level for the 2019 setups (FG5-220, X-version) and 1.20 m for the 2004 setups with the original gravimeter version of FG5-220. For the Wank stations, the reference height h = 1.200 m (above floor point) has been chosen for comparison reasons. The average of a station determination has been calculated as the arithmetic mean of the different setups. Before, a setup mean was calculated as a weighted mean of the runs (no. of drops is the weight of a run). Std.dev. is the standard deviation calculated from the drop scatter.

Site	Orientation: N(North)/S(South)	Mean Epoch	Drops	g1.200 m [μm/s2]	Std.dev. (Single gi)
Wank Berg (2004), δg/δh = −3.877 μm/s2/m, href =1.200 m
Run 1/setup1	S	1 December 2004,10:19	198	9,803,733.437
Run 2/setup1	S	1 December 2004, 4:27	596	9,803,733.463
Run 3/setup2	N	2 December 2004, 00:40	1196	9,803,733.473
Average			1990	9,803,733.465	0.085
Wank Berg (2019), δg/δh = −3.877 μm/s2/m, href =1.200 m
Run 1/setup1	S	20 September 2019, 22:38	1193	9,803,733.483
Run 2/setup2	N	21 September 2019, 21:32	1197	9,803,733.457
Average			2390	9,803,733.470	0.033
Wank Tal (2004), δg/δh = −2.847μm/s2/m, href =1.200 m
Run 1/setup1	S	3 December 2004, 13:20	150	9,805,844.342
Run 2/setup1	S	3 December 2004, 15:14	150	9,805,844.335
Run 3/setup1	S	4 December 2004, 00:54	1392	9,805,844.296
Run 4/setup2	N	4 December 2004, 14:06	698	9,805,844.348
Run 5/setup2	N	4 December 2004, 21:32	799	9,805,844.362
Average			3189	9,805,844.330	0.105
Wank Tal (2019), δg/δh = −2.847μm/s2/m, href =1.200 m
Run 1/setup1	S	23 September 2019, 20:03	1197	9,805,844.276
Run 2/setup2	W	24 September 2019, 12:27	797	9,805,844.267
Average			1994	9,805,844.271	0.061

in the Appendix A, like the applied vertical gradient, reference height of the result, mean epoch, single run results.

Besides the numerical details of all station determinations since 2004 (Table A1, Table A2 and

Table A3. Absolute gravity values of the FG5-220 measurements at the top of Mt. Zugspitze (facilities of Environmental Research Station Schneefernerhaus, DFMG Deutsche Funkturm GmbH and GFZ German Research Centre for Geosciences). The gradient insensitive sensor height depends on the gravimeter setup and is about 1.25 m above floor level for the 2019 setups (FG5-220, X-version) and 1.20 m for the 2004 setups with the original gravimeter version of FG5-220. The average of a station determination has been calculated as the arithmetic mean of the different setups. Before, a setup mean has been calculated as a weighted mean of the runs (no. of drops is the weight of a run). Std.dev. is the standard deviation calculated from the drop scatter.

Session	Orientation: N(North)/S(South)	Mean Epoch	Drops	ghref [μm/s2]	Std.dev. (Single gi)
Zugspitze Telekom (2004), δg/δh = −4.653 μm/s2/m, href =1.200 m
Run 1/setup1	S	18 September 2004, 11:14	442	9,800,621.483
Run 2/setup1	S	18 September 2004, 14:47	249	9,800,621.475
Run 3/setup2	S	18 September 2004, 23:58	1292	9,800,621.490
Average			1983	9,800,621.485	0.103
Schneefernerhaus 200 (2004), δg/δh = −3.505 μm/s2/m, href =1.200 m
Run 1/setup1	N	9 September 2004, 17:28	546	9,801,546.893
Run 2/setup2	N	10 September 2004, 01:03	938	9,801,546.854
Average			1484	9,801,546.873	0.148
Schneefernerhaus 202 (2016), δg/δh = −3.416 μm/s2/m, href =1.250 m
Run 1/setup1	ESE	28 September 2016, 13:56	598	9,801,547.864	0.075
Zugspitze ZUGOG (2018), δg/δh = −5.045 μm/s2/m, href =1.250 m
Run 1/setup1	N	15 October 2018, 21:12	2386	9,800,631.389
Run 2/setup1	N	16 October 2018, 19:01	3584	9,800,631.378
Run 3/setup2	S	17 October 2018, 19:47	3366	9,800,631.368
Run 4/setup2	S	18 October 2018, 08:03	198	9,800,631.337
Run 5/setup3	S	18 October 2018, 13:34	298	9,800,631.355
Run 6/setup3	S	19 October 2018, 17:14	3186	9,800,631.348
Average			13,018	9,800,631.366	0.095
Zugspitze ZUGOG (2019), δg/δh = −5.045 μm/s2/m, href =1.250 m
Run 1/setup1	N	26 September 2019, 10:18	194	9,800,631.451
Run 2/setup1	N	26 September 2019, 20:24	1798	9,800,631.452
Run 3/setup2	S	27 September 2019, 11:41	485	9,800,631.432
Average			2477	9,800,631.442	0.091

), Figure A1 in the Appendix A shows two additional examples of graphical compilations which demonstrates that the precision of the measurements at Zugspitze with the FG5-220 in 2004 and in 2018 were similar (standard deviation in 2004: 103 nm/s²; 2018: 95 nm/s²). The much larger number of measurements in 2018 is attributable to the calibration of the new superconducting gravimeter OSG#052 at ZUGOG.

For the comparison of results since 2004, the relative and absolute gravity observations have been combined to obtain common reference points with comparable g-values for the different epochs. The transfer of observed absolute g-values to another position with relative gravimetric Δg-values was needed for comparison reasons especially for the measurements at Mt. Zugspitze. At Mt. Wank, the absolute gravity determinations (2004, 2019) were performed at similar sensor heights above the ground markers. Thus, only vertical gravity gradients have to be considered for transferring g-results to the chosen sensor reference height of 1.200 m. The Δg-values from relative gravimetry used to transfer absolute observations at Mt. Zugspitze to common points are compiled in

Table 3. Gravity differences Δg observed by relative gravimetry at Mt. Zugspitze. All ties are referred to a reference height of 0.260 m above floor level which is approx. the sensor-height of the CG-3 gravimeter (sensor-height CG-6 ≈ 0.22 m). Std.U is the standard uncertainty calculated in a least squares adjustment as the standard deviation of the resulting gravity difference.

From	To	Epoch	Δg	Std.U	Gravimeter	Remarks
(href = 0.260 m)			[μm/s2]		Scintrex
Schneef. 308	Schneef. 200	2004	−22.616	0.008	CG-3 #4492	Point 308 inside Schneefernerhaus, witness point
Schneef. 308	Schneef. 202	2011	−22.333	0.012	CG-3 #4492	Tie to new abs. point
Schneef. 308	Schneef. 202	2016	−22.328	0.018	CG-3 #4492	Tie to new abs. point
Schneef. 202	Zug. Telekom	2016	−925.618	0.020	CG-3 #4492	Tie between 2 abs. points
Zug. Telekom	Zug. ZUGOG	2018	+10.893	0.009	CG-6 #0069	Tie between old and new absolute point at summit
Zug. Telekom	Zug. ZUGOG	2019	+10.910	0.022	CG-6 #0069	Tie at summit like in 2018

. The connection within Schneefernerhaus between point 202 (absolute point) and 308 (witness point) were measured in 2011 and 2016. The two results agree within 0.005 μm/s² which is excellent. The tie between the two Zugspitze points Telekom and ZUGOG was observed in 2018 and again in 2019. The discrepancy is 0.017 μm/s² only which is statistically not significant and can be related to measurement uncertainties as well as to differential gravity variations between the points due to assumed changes in water storage within the rock.

Table 4. Absolute gravity values (at reference height h_ref = 1.200 m or 1.250 m above floor mark) of the FG5-220 stations at Mt. Wank and Mt. Zugspitze as determined in the period 2004 to 2019. Scheme 5. which is derived as an empirical estimate. Because of the assumptions in the uncertainty estimates, they are given here as rounded values. In case of transferring an absolute observed g-value to another point by relative gravimetry (centred), the uncertainty has been increased from 0.02 μm/s² to 0.03 μm/s².

Station	Date	href [m]	g [μm/s2]	Std.U	Remarks
Wank Berg	1–2 December 2004	1.200	9,803,733.465	0.02	Absolute observation on mountain top
Wank Berg	20–22 September 2019	1.200	9,803,733.470	0.02
Wank Berg		Δg2019–2004 = +0.005 μm/s2		0.03
Wank Tal	3–5 December 2004	1.200	9,805,844.330	0.02	Absolute observation on mountain foot
Wank Tal	23–24 September 2019	1.200	9,805,844.271	0.02
Wank Tal		Δg2019–2004 = −0.059 μm/s2		0.03
Schneef. 202	9/10 September 2004	1.250	9,801,548.072	0.03	Abs. obs. on Schneefernerhaus 200, centred
Schneef. 202	28 September 2016	1.250	9,801,547.864	0.02	Abs. obs. on Schneef. 202
Schneef. 202		Δg2016–2004 = −0.208 μm/s2		0.04
Zug. Telekom	18/19 September 2004	1.200	9,800,621.485	0.02	Absolute observation on Telekom
Zug. Telekom	28 September 2016	1.200	9,800,621.254	0.03	Abs. obs. on Schneef. 202, centred
Zug. Telekom	15–20 October 2018	1.200	9,800,621.157	0.03	Abs. obs. on ZUGOG, centred
Zug. Telekom	26–27 September 2019	1.200	9,800,621.216	0.03	Abs. obs. on ZUGOG, centred
Zug. Telekom		Δg2019–2004 = −0.269 μm/s2		0.04

summarizes the epoch results from 2004 to 2019. For Mt. Zugspitze, the common points are Telekom and Schneefernerhaus 202. The epoch comparisons are depicted in Figure 5. First of all, we focus on the Wank results. Wank Berg (summit) does not show any change between 2004 and 2019. The very small difference of 0.005 μm/s² indicates a long-term stability. Wank Tal (foot, valley) shows a decrease in gravity of 0.06 μm/s² which is not a significant discrepancy (95% confidence level) but may indicate a real change which can possibly be caused by hydrological variations in the subsurface sediments and rocks. We have tried to align the gravity variations with groundwater data provided by the Hydrological Service of the Bavarian Environmental Agency. Based on the questionable hypothesis that groundwater levels measured at two nearby groundwater gauges are representative for the whole of the Loisach valley (river Loisach represents the western edge of the Ester Mountains, roughly following road B23 in Figure 1), we estimated the related gravity change at Wank Tal between the observational epochs 2004 and 2019. The resulting effect, however, indicates an insignificant increase in gravity (0.002 μm/s²) and cannot explain the observed decrease.

Also a local uplift of the crustal surface would result in a gravity decrease but seems to be unrealistic. We conclude from the Wank measurements that the long-term situation (over almost two decades) is stable. This will be a helpful premise for assessing the Zugspitze measurements.

Figure 5 implies a secular trend of up to −0.02 μm/s² per year for the sites at Zugspitze. The observed gravity rate (trend) between 2004 and 2016 at site Schneefernerhaus 202 and the rate between 2004 and 2019 at site Telekom are quite similar and are each statistically significant. Just studying the observations from 2016 to 2019 at Telekom, no contradiction to the rate of about −0.02 μm/s² per year emerges, cf. Section 2.2. Of course, short-term variations due to hydrological effects are superimposing the long-term trend. Therefore, the 15-year time base becomes useful. The newly available OSG#052 will solve the issue with short-term gravity variations.

In 2016, the relative tie between the twin stations at Zugspitze has been measured by relative gravimetry.

Table 5. Gravity differences between the two Zugspitze stations Telekom (summit) and Schneefernerhaus 202 (≈300 m below summit) measured in 2004 (absolute gravimetry and centring) and in 2016 (relative gravimetry).

From	To	Epoch	Δg	Std.U	Remarks
(href = 1.200 m)	(href = 1.250 m)		[μm/s2]
Zug. Telekom	Schneef. 202	September 2004	+926.587	0.030	Absolute observ. on Schneef. 200 (transferred to 202) and on Zug. Telekom
Zug. Telekom	Schneef. 202	September 2016	+926.618	0.020	Relative gravity tie
	Δg2016–2004 = +0.031 μm/s2			0.036

compares this result with the Δg-result from 2004 which is based on absolute measurements. They differ by 0.03 μm/s² only (no significance). This implies that the relative conditions w.r.t. mass distribution (water, snow, ice) between site Schneefernerhaus 202 and site Telekom at the respective dates in September were largely constant.

2.2. Superconducting Gravimetry

In September 2018, the Zugspitze Geodynamic Observatory Germany has been set up by GFZ at the summit of Mt. Zugspitze including the observatory superconducting gravimeter (SG) OSG#052 by GWR Instruments, Inc., a permanent GNSS station and a local hydro-meteorological sensor network [15]. During the first simultaneous measurements of the absolute gravimeter FG5-220 and the OSG#052 at the end of September 2018, the SG showed an instrumental malfunction accompanied by a large negative drift of some nm/s²/day and several steps after being transported at operating temperatures of 4 K from GFZ to Mt. Zugspitze. An amplitude factor of −746.68 nm/s²/V was determined with a reduced uncertainty of 1-σ = 1.30 nm/s²/V similar to the one determined at Sutherland station, South Africa, where the instrument was located before transferring the SG back to Germany (−748.3 nm/s²/V). However, the first absolute measurements cannot be used as reference value for the drift estimation, as the SG had to be warmed up and cooled again for re-initialization at the end of December 2018. Since then, the SG has been in nominal mode. The continuous time series of gravity residuals from the OSG#052 so far provides seasonal minimum gravity values on 1 October 2019 and 20 September 2020 after reduction of Earth’s body and ocean tides, polar motion, and atmospheric mass movements [15] which is consistent with the absolute gravity measurements. The time series gives evidence that the periods of absolute gravity observations at late September were well chosen to keep the aliasing effects as small as possible.

Within the context of applied reductions, we have to note that non-tidal loading effects of the Atlantic Ocean (North Sea and Gulf of Biscay), which are forced by the atmosphere, are not considered and may have a significant effect on the AG and SG measurements during storm surges in the ocean. In [34], crustal deformation has been modelled considering the loading of a typical storm surge of 2 m in the southern North Sea. The predicted maximal impact on gravity in the German Alps is up to 0.01 μm/s². The non-tidal loading effects of seas like the Mediterranean Sea are of much smaller magnitude due to the smaller amplitude of the surge water height and the much smaller areal dimension but have not been investigated for this article. The effect of non-modelled ocean or sea signals on the AG trend result is negligible.

As a reliable assumption, largest aliasing effects on absolute measurements may be related to hydrological processes in the vicinity of the observatory. More specifically, these are precipitation events for periods around the seasonal minimum gravity values. Figure 6 shows hourly gravity variations from OSG#052 and daily precipitation heights at the summit station Zugspitze extracted from the DWD Climate Data Center [35]. The high correlation is clearly visible. Rain events in September and October generally cause a rapid cumulative gravity increase followed by an equally fast but only partial decrease and a slower subsequent decline due to the lagged drainage back to the gravity level before the specific rain event. Snow events from November lead to continuous gravity rise due to an accumulative growing of the snowpack over the winter months. The aliasing effect from precipitation can be quantified for the second parallel campaign at ZUGOG from 26 to 27 September 2019 with a gravity increase of 0.04 µm/s² (SG) compared to the seasonal minimum on 1 October 2019. Figure 7 compiles daily precipitation heights from [35] at least 3 weeks before and during the absolute measurements at Mt. Zugspitze in 2004, 2016, 2018 and 2019 (cf. Table 4). It can be seen that all absolute gravity measurements were carried out during completely dry periods—except 2019. This explains the positive deviation from the trend line in Figure 5. Moreover, the 2004 and 2019 measurements show some precipitation in the week before the absolute measurements. However, the effect of a daily maximum of 15 mm precipitation 4 days before the absolute measurements in 2004 should not have a significant impact on the FG5 measurements, whereas the negative deviation for the absolute measurements in October 2018 can be assigned to the anomalous heat and drought of summer 2018.

2.3. GNSS Observations

Today, continuously operating stations of the Global Navigation Satellite Systems (CO-GNSS stations) allow the determination of coordinates in the range of a few millimeters and the detection of changes in position by repeated observations. Therefore, based on the repeated observations, station velocities can be estimated. This has been demonstrated by [4] for the Alpine region. Long-term observations with GNSS [36] are not available for Mt. Zugspitze itself. The situation is different for the mountain top of Mt. Wank. The Bavarian Mapping Agency operates a permanent GNSS reference station as part of the Satellite Positioning Service (SAPOS) of the German Surveying and Mapping agencies. Based on a network of CO-GNSS stations, SAPOS provides the official spatial reference frame for Germany. CO-GNSS data of the station on the summit of Mt. Wank has been used to determine the horizontal and vertical motion between the years 2007 and 2016. Even GNSS observations from 2004 are available, but the station was moved to a new marker in the summer of 2007. The relocation was necessary because the old station was only attached to the railing on top of a building. This site characteristic does not guarantee that movements of the surface and movements of the building are decoupled. The new monument is founded in bedrock and is not more than a meter away from the old point. The new setup thus meets the requirements for observing geodynamic processes. The analysis of the data between 2007 and 2016 follows the same principles as the analysis presented in [4] but this time it only covers the southern part of the Bavarian SAPOS network including several stations of the International GNSS Service (IGS) network [37] and the EUREF Permanent Network [38] to ensure a reliable geodetic datum realization. The GNSS analysis is consistent with the conventions of the International Earth Rotation and Reference Systems Service (IERS) for the determination of the ITRF [39]. The GNSS-specific guidelines are in agreement with IGS guidelines for the 2nd data reprocessing campaign [40]. Therefore, corrections for solid Earth tide, permanent tide, and solid Earth pole tide are applied as described in the IERS conventions. Ocean tide loading is estimated using the FES2004 model [41] and the atmospheric tide loading caused by the semidiurnal constituents S1 and S2 is estimated following the model of [42]. Non-tidal loadings due to atmospheric pressure, ocean bottom pressure, or surface hydrology are not reduced.

In order to guarantee the consistency of the analysis over several years, we used identical correction models over the entire time span and used reprocessed GNSS satellite orbits that refer to the IGb08 reference frame [43]. The analysis of the GNSS data (GPS and GLONASS) for each day was performed with Bernese GNSS Software V5.2 [44]. Based on these daily solutions, a multi-year solution with a position for a specific date and constant velocity for each CO-GNSS station was computed. This includes an iterative time series analysis to detect outliers and discontinuities in the daily station positions. In the multi-year solution, the geodetic datum is realized with respect to the coordinates and velocities of selected reference stations. The station velocity represents the mean displacement of the CO-GNSS station 1285 (Wank summit) over the entire investigation period in meters per year.

Figure 8 shows the position residuals for the site 1285, which is the SAPOS reference station on the summit of Mt. Wank. The time-series of residuals for the horizontal components are smaller having a standard deviation of 1.1 mm for the north and 1.3 mm for the east component, while the standard deviation for the height component of 2.5 mm is larger by approximately a factor of two. The increase in noise for the height component is typical and caused by the geometry of the GNSS satellite constellation. The position time series are cleaned from seasonal periodical signals and offsets. The latter are often caused by equipment changes (receiver or antenna) or alterations to the setup. Seasonal signals are common and can be caused, for example, by the surrounding hydrology or thermal expansion. The estimation of offsets and periodic signals can be performed either by a software program called FODITS [45], which is part of BERNESE 5.2, or by a program called HECTOR [46]. HECTOR offers both, the estimation of the model parameters (velocity/trend, bias and/or periodic signals) and the parameters of the chosen noise model using the Maximum Likelihood Estimation (MLE) method. In our case, the program HECTOR was used to estimate the annual periodic signals at station 1285, which have an amplitude of 0.85 mm for the north, 1.44 mm for the east and 0.78 mm for the height component. Semiannual signals were not significant and therefore not estimated. The annual linear velocities for this analysis (marked as “continuous”) are given in

Table 6. Velocities of the GNSS site 1285 based on two different approaches. The accuracy estimates for the “continuous” approach are based on the analysis with program HECTOR. The standard deviations s for the “campaign” approach are crude estimates derived by scaling the internal error estimates by a factor of 10 which ensures to have more realistic figures.

Mode	Period	North [mm/yr]	East [mm/yr]	UP [mm/yr]
continuous	2007–2016	14.98 s = 0.11	20.55 s = 0.18	0.29 s = 0.16
campaigns	2004–2019	16.18 s = 0.1	21.25 s = 0.1	0.18 s = 0.2

for each component.

The main drawback of this first GNSS analysis is that it only covers the years between 2007 and 2016. However, the absolute gravity measurements of this study were conducted in the years 2004 and 2019. It is rather unlikely that geodynamic signals based on plate tectonics or isostatic adjustment show a sudden change. Therefore, we argue that the mean velocity determined between 2007 and 2016 does not significantly deviate from the mean velocity expected between 2004 and 2019. To account for uncertainties of this assumption, we estimated the velocity of the SAPOS station on Mt. Wank using an alternative approach.

As mentioned earlier, GNSS observations have been available since 2004 up until now. A repeated and complete analysis that covers the last years is not yet available. The reason is that the first analysis is based on orbits, Earth rotation parameters (ERPs) and antenna correction models based on the IGb08. In recent years we use the new IGS14 [47] as realization of the International Terrestrials Reference System (ITRS). A complete consistent and continuous analysis between 2004 and 2019 is only possible, when reprocessed orbits and EOPs in IGS14 will be available, which is not yet the case. Therefore, we have processed the GNSS data of station 1285 together with 23 CO-GNSS sites in Europe, which are part of the global IGS14 network using the standards of the IGS14. These sites realize the datum and allow the estimation of coordinates and velocities of the CO-GNSS site 1285. Two weeks of data were processed in 2004 and 2019 covering the time of the gravimetric measurement campaigns in 2004 and 2019. As mentioned above, the SAPOS site on Mt. Wank was moved to a new location in 2007. Therefore, we have processed another three weeks of data in 2007, when data was recorded at the old location (0285) and the new site (1285) in parallel. This allows the precise estimation of the baseline components between the two locations. The multiyear solution is again based on daily solutions. However, this time there are no continuous time series, but measurements from the multi-week campaigns in 2004, 2007 and 2019. To determine the velocity of station 0285 and 1285, we specify the condition that the velocities of these two stations should be the same over the entire period.

The advantage of this alternative approach is that we cover the entire time between 2004 and 2019. The drawback is that based on this data we are not able to estimate offsets caused by changes in the setup and we cannot compute seasonal signals. Nevertheless, mean velocities for station 1285 based on this last analysis is given in Table 6 (marked as “campaigns”). The results between these two approaches differ slightly, which is mainly due to the different setups. In the continuous analysis we have observed several offsets that have been corrected. This cannot be done for the campaign style analysis. We see the largest discrepancy in the velocity of the north component which is about 1.2 mm/yr. The velocity difference of 0.7 mm/yr in the east component is slightly smaller. The most important result is that the vertical velocity in both analyses is very small and can hardly be considered significant in terms of its standard deviations. Based on this study we can conclude that we do not see any vertical motion on the summit of Mt. Wank.

The gravity point itself lies in the basement of the cable car station. The distance between the SAPOS stations and the point in the basement is roughly 250 m with a height difference of approximately 30 m. The height determination between the SAPOS station and the point in the basement was carried out using a combination of GNSS observations and spirit levelling. The results were consistent and did not show a significant height change between the gravity point and the SAPOS station for the epochs 2004 and 2019. Therefore, we can conclude that also the height of the gravity point did not change in time.

A concrete statement on the vertical movement of Mt. Zugspitze on the basis of the analysis of GNSS observations cannot be made for the time being. A CO-GNSS station nearby ZUGOG has only been installed in 2018 [15], but it takes well over three to five years to determine even small, significant vertical movements.

3. Results Compared with Predicted Secular Variations Caused by Glacier Retreat

Secular gravity variations are affected by mass variations of nearby glaciers. In [13], a combination of relative and absolute gravimetry is used to validate geodetic mass balance estimates of Vernagtferner, Austria. In [48], the authors evaluate the contribution of glacier retreat in the Austrian Ötztal and Stubai valleys on absolute gravity values observed between 1987 and 2009 at the AG reference station in Obergurgl, Austria. They show that around 2/3 of the observed positive trend of 14 nm/s²/yr can be explained by glacier mass loss. The observed trend is in the same order of magnitude as the one discussed in the present paper for Mt. Zugspitze. The opposing sign of the trends (−20 nm/s²/yr in Figure 5 and +14 nm/s²/yr in [48]) is caused by the fact that glaciers in the Zugspitze area are located below the AG sites (summit and Schneefernerhaus), while Obergurgl is a valley station and the relevant ice masses are located above it. This also causes glacier induced gravity trends in Obergurgl to counteract small negative gravity trends caused by the general uplift of the Alpine area, while at Mt. Zugspitze effects from ice mass loss and uplift add up. In the following, we quantify the contribution of glacier retreat at Mt. Zugspitze on the observed gravity trends.

The Zugspitze area comprises three small mountain glaciers which have all experienced considerable mass loss since 1892 when Finsterwalder and Jäger created the first map of the area which is usable for quantitative analysis, see [49]. The mass loss is in line with the general retreat of glaciers in the Alps since the end of the Little Ice Age around 1850 [50]. The three glaciers in the Zugspitze area are Höllentalferner (HTF, mean height 2400 m above sea level) which is located to the northeast of Zugspitze summit, Nördlicher Schneeferner (NTF, 2630 m) located at the Zugspitze plateau almost below Schneefernerhaus, and Südlicher Schneeferner (SSF, 2550 m) located further away from Schneefernerhaus on the southern side of the plateau. The areal extend of all three glaciers at epochs 1999 and 2018 are shown in Figure 9. In this period Höllentalferner has lost about 38% of its area (area decreased from 0.26 km² to 0.16 km²), Nördlicher Schneeferner has lost about 58% (from 0.36 km² to 0.15 km²) and Südlicher Schneeferner about 84% (from 0.12 km² to 0.02 km²).

Systematic mapping of glacier area and volume was conducted by glaciologist at the Bavarian Academy of Sciences and Humanities since the 1960s with roughly decadal sampling, see [49] and references therein. Maps of glacier surface elevations for most epochs are available at the project website http://www.bayerische-gletscher.de (accessed on 9 November 2020). From these maps the contribution of glacier mass to gravity acceleration measured at Zugspitze summit and Schneefernerhaus are evaluated using an average density of 900 kg/m³ for volume to mass scaling. The related gravity effect is computed from 3-dimensional modeling using rectangular prisms [51] with a basis area of 2m × 2m. Unfortunately, epochs of glacier mapping and gravity observations do not coincide. However, glacier volume as well as the corresponding gravitational attraction have decreased almost linearly since the 1980s, so that the linear trend derived from glacier maps between epochs 1999 and 2018 can be assumed to be a good estimate for the glacier contribution to the gravity trend between 2004 and 2019 (see Figure 5).

Figure 10 shows the gravity effect of glacier masses since around 1980. The left panel shows the gravity effect evaluated at AG station Zugspitze Telekom, the right panel shows the gravity effect evaluated at AG station Schneefernerhaus. In both panels the individual contributions of all three glaciers are shown along with their combined effect. We observe that SSF has no significant contribution (below observational precision) over the whole time span, while HTF and NSF have. Because HTF is closer to the summit station Zugspitze Telekom, its contribution dominates there, while NSF dominates at Schneefernerhaus. The combined effect of HTF and NSF is similar at both AG sites. This fits well to observational evidence from absolute and relative gravimetry (see Section 2).

The linear trend caused by glacier retreat between epochs 1999 and 2018 amounts to −12 nm/s²/yr at both AG sites. This is more than half the observed trend of −20 nm/s²/yr. It is likely that glacier retreat is the main contributing process causing the gravity decline at Mt. Zugspitze.

4. Summary and Conclusions

The absolute gravity determinations of FG5-220 at the top of Mt. Zugspitze in 2004, 2016, 2018 and 2019 show gravity decreases of 0.21 μm/s² (2016–2004), 0.33 μm/s² (2018–2004) and 0.27 μm/s² (2019–2004). These results are estimated with standard uncertainties of 0.03 to 0.04 μm/s² and are highly significant. Deducing an average value of yearly g-changes, a trend of about −0.02 μm/s²/yr is obtained. The variability of the absolute g-results at Mt. Zugspitze from 2016 to 2019 can be explained with the continuous record of the superconducting gravimeter OSG#052 (since beginning of 2019), which reveals the gravity dependency on rain and snow precipitation. The epochs of absolute measurements were well chosen, always between mid of September to end of October (conditions with minimum snow coverage) to avoid aliasing effects in the derivation of a secular trend. But short-term hydrological effects of some 0.01 μm/s² are still disturbing the trend determination. In the future, the common evaluation of episodic absolute gravity measurements and continuous records of the superconducting gravimeter will overcome the lack of non-continuous time series.

In parallel to the Zugspitze measurements in 2004 and 2019, absolute g-observations were performed at Mt. Wank which also belongs to the Northern Limestone Alps but is classified as part of the Bavarian Prealps. The horizontal distance between Zugspitze and Wank is approximately 15 km. The observed gravity changes after the time span of 15 years is almost zero at the site close to the summit of Mt. Wank and it is 0.06 μm/s² at the foot of Mt. Wank. Thus, for Wank summit a stable situation is implied. GNSS data continuously recorded between 2007 and 2016 as well as GNSS measurement campaigns in 2004, 2007 and 2019 confirm that there is no significant vertical motion of the summit. At the foot of Mt. Wank a small gravity variation has been measured gravimetrically, but is statistically not significant. This site is located at the edge of the valley of the Loisach River where hydrological variations within the valley sediments may cause such a temporal change in gravity. It is noteworthy how different the gravity acceleration field of the Earth’s crust is behaving with respect to time over a lateral distance of 15 km. Whereas the Wank situation has to be assumed as stable over a period of 15 years, a prevailing gravity decline is determined for the top of Mt. Zugspitze.

Published geodetic results from geometric levelling and from GNSS observations state a vertical uplift up to more than 2 mm/yr for the central ridge of the Alps which becomes less to the margins of the mountain chain [3,4]. In [52], a summary is given listing published observations of the ratio between temporal variations of gravity and height in previously glaciated areas. The proportionality factor is about −0.002 μm/s²/mm (provided here as a rounded average but might be wrong by 10% or even more). Assuming a vertical uplift of Mt. Zugspitze of about 1.5 mm/yr and applying the above given proportionality factor, the vertical movement would result in a gravity change of −0.003 μm/s²/yr only. Adding this secular contribution to the modelled effect of glacier retreat yields -0.015 μm/s²/yr which explains 75% of the observed gravity trend at the summit of Mt. Zugspitze. The discrepancy of 25% accumulates to 0.075 μm/s² between the AG epochs 2004 and 2019. This is geodetically not significant considering an observational uncertainty of 0.04 μm/s² as well as an undefined uncertainty of the model prediction but may also reflect a small unconsidered inter-annual hydrological signal in the local subsurface (diminishing permafrost) or local mass variations from debris flow or rock fall.

A continuation of the gravimetric monitoring embedded in an intensive interdisciplinary research is needed to examine and demonstrate the reasons for the gravity variations on inter-annual and climate-relevant decadal scales. Appropriate steps have already been initiated within a cooperation of geodesists, geophysicists and hydrologists, see also [15].