An Exponential Algorithm for Bottom Reflectance Retrieval in Clear Optically Shallow Waters from Multispectral Imagery without Ground Data

Abstract

Bottom reflectance is a significant parameter characterizing the bottom types for clear optically shallow waters, typically in oceanic islands and reefs. However, there is not an effective physics-based method for inverting the bottom reflectance using multispectral images. In this study, we propose a novel approach for quantitatively inverting the bottom reflectance at 550 nm without the dependence of in situ bottom reflectance data or any other priori knowledge. By linking different pixels in the same image and utilizing the strong linear relationship between their water depths and the spectral related parameters, the global situation of the radiative transfer model was constrained, and an exponential relationship between the log-transformed ratio of the blue–green band reflectance and the bottom reflectance was established. The proposed model was checked by comparing the Hydrolight input bottom reflectance with that inverted from Hydrolight simulated spectrum, resulting in correlating well. Our method has successfully performed using WorldView-2 and Landsat-8 in Midway Island in the North Pacific Ocean, with the cross- and indirectly checking and obtained reliable and robust results. In addition, we assessed the potential of the quantitative bottom reflectance in benthic classification and inversion ranges under different bottom reflectance. These results indicated that compared with those methods relying on in situ data or hyperspectral imagery, our algorithm is more likely to efficiently improve the parameterization of bottom reflectance, which can be very useful for benthic habitat mapping and transferred to large-scale regions in clean reef waters, as well as monitor time-series dynamics of oceanic bottom types to forecast coral reef bleaching.

1. Introduction

In the context of deteriorating marine environment and increasing threats [1,2], detailed, consistent, and accurate information in real time on seafloor conditions is critical for sustainability and conservation of marine ecosystems. This is especially important for oceanic islands and reefs with high organic productivity to support necessary habitats for oceanic flora and fauna [3,4]. Bottom types, such as coral reef, sand, and rubble play an important role in understanding the physical benthic habitat and developing management strategies [5]. Moreover, bottom reflectance is a significant indicator to effectively monitor the composition of bottom types.

Remote sensing, as a low-cost and time-efficient technology, has attracted substantial attention and prompted the combination with other technologies, such as multibeam echosounders [6,7]. Remote sensing images are usually applied to optically shallow waters, where the optical information of the bottom types in the visible wavelengths can be obtained radiometrically by optical sensors above the water, typically in clean oceanic islands and reefs with depth less than 30 m. The most widely used spectral range is blue–green bands that have a stronger penetrating ability, because the attenuation of visible wavelengths in seawater is weaker compared with other longer wavelengths [8,9]. In recent decades, the methods applied to explore the seafloor through satellite remote sensing can be roughly divided into two categories: empirical methods and model based analytic algorithm. These empirical methods are also called statistical algorithms, such as a neural networks [10], supervised classification [11], unsupervised classification [12], cluster analysis [13], object-based classification [14,15], and feature selection based on maximum likelihood classifier [16], which map the bottom types effectively without considering any physical mechanism. Such methods rely heavily on the availability of a large volume of field-based training data for targeting a statistical robustness. This is impracticable to collect in in-situ bottom types or reflectance in dangerous areas that are inaccessible by ship or unmanned aerial vehicles. In addition, some uncertainties will remain due to differences in the optical conditions of different image scenes when transfer the training model to other regions.

The other method that based on radiative transfer model can be applied to both hyperspectral and multispectral imagery which can simultaneously invert the bottom reflectance and bathymetry, even water optical parameters [17,18,19,20,21,22]. The major advantage of using hyperspectral data is that it can directly invert water properties without in situ data. But compared the two data sources, there are some spatial and temporal resolution limitations of hyperspectral data, and multispectral remote sensing has a longer development history and richer data source, such as Landsat-5/7/8, Sentinel-2, WorldView-2/3, GeoEye-1, QuickBird, IKONOS, Planet Dove, Gaofen-1/2, and other medium- and high-resolution images. However, the number of bands for multispectral data is inadequate to separate the components of the bottom reflection and water column scattering; typically, water depth (from the top of a bottom-type object to the surface of the water) will interfere with the identification of bottom types [10,23,24]. In this scenario, some ground-based measurements or empirical coefficients will be needed to reduce the number of unknown parameters [25,26,27,28,29], which makes it difficult for a precise and large-scale mapping of coral reefs, especially a quantitative bottom reflectance without any prior knowledge. Furthermore, pixel by pixel iteration of high spatial resolution imagery through a physics-based approach is inefficient and time-consuming work.

To address the above-mentioned problems, we integrated an empirical and semi-analytical model and aim to propose a novel relationship between the subsurface reflectance and bottom reflectance without ground–based measurements or a priori information. The empirical model based on the log-ratio model of Stumpf et al. [30] was used to constrain the entire situation, to build more equations and reduce the unknown parameters of the semi-analytical model. Through the combination of the log-ratio model and semi-analytical model, we can iteratively invert the bottom reflectance using the semi-analytical model of Lee et al. [19] (the specific algorithm of this calculation process is in Appendix A). Then, we can build an exponential model between the bottom reflectance we inverted above and the log-transformed subsurface reflectance of blue–green bands, which can invert the bottom reflectance quantitatively with most multispectral remote sensing images and not interfered by underwater terrain; i.e., the Log rotation Ratio and Semi-analytical model (we called LR-S model). We used two different multispectral remote sensing images (i.e., WorldView-2 and Landsat-8) to perform the method in Midway Island. The model and results were then checked using the Hydrolight simulation dataset, a benthic map of the Allen Coral Atlas, and in-situ data of multibeam soundings.

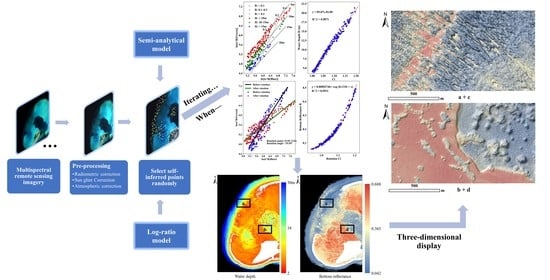
2. Methods

2.1. Basic Model

According to single- or quasi-single-scattering theory and the single radiation transmission process in optically shallow water, the subsurface remote-sensing reflectance can be approximated and simplified as a sum of the contributions from the water column and the bottom [7,18].

$$r_{rs}=r_{rs}^{dp}\left[1-\exp \left(-0.75\times gH\right)\right]+r_b\exp \left(-gH\right)$$

(1)

where $r_{rs}^{dp}$ is the subsurface remote sensing reflectance of optically deep waters, g is the sum of the diffuse attenuation coefficients of upwelling light, $r_b$ is the ratio of the bottom irradiance reflectance to $\pi$, and H is the water depth. The bottom is assumed to be a Lambertian reflector.

By taking the logarithm of Equation (1) and combined the subsurface reflectance $r_{rs1}$ with $r_{rs2}$ of the blue–green bands:

$$\begin{gathered} H=\left(-\frac{1}{2g_1}\right)\ln \left[\left(r_{rs1}-r_{rs1}^{dp}\right)/\left(r_{b1}-A{r}_{rs1}^{dp}\right)\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left(-\frac{1}{2g_2}\right)\ln \left[\left(r_{rs2}-r_{rs2}^{dp}\right)/\left(r_{b2}-A{r}_{rs2}^{dp}\right)\right] \end{gathered}$$

(2)

In the HOPE model of Lee et al. (1999), $\rho \left(\lambda \right)$ is expressed as $\rho \left(\lambda \right)=B{\rho }_{normal}\left(\lambda \right)$, for $\rho \left(\lambda \right)$ a 550-nm-normalized albedo shape ${\rho }_{normal}\left(\lambda \right),$ which was a linear function that was used, where B is the bottom albedo value at 550 nm (green band), then the bottom reflectance in the blue band was simplified. Thus, we can establish a connection between the bottom reflectance of blue ($r_{b1}$) and green ($r_{b2}$) wavelength, which is $\ln \left[r_{b1}\right]=\mathrm{c}\ast \ln \left[r_{b2}\right]$. In this way, Equation (2) can be rewritten as:

$$\begin{gathered} \ln \left[r_{b2}-A{r}_{rs1}^{dp}\right]=\left[\left(\frac{1}{2g_1}\right)/\left(\frac{1}{2g_1}+\frac{c}{2g_2}\right)\right]\ln \left[r_{rs1}-r_{rs1}^{dp}\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left[\left(\frac{1}{2g_2}\right)/\left(\frac{1}{2g_1}+\frac{c}{2g_2}\right)\right]\ln \left[r_{rs2}-r_{rs2}^{dp}\right]+H/\left(\frac{1}{2g_1}+\frac{c}{2g_2}\right) \end{gathered}$$

(3)

where $A=\exp \left(0.25\times gH\right)$.

Based on Equation (2), Stumpf et al. [30] built the log-ratio model (the ratio of the logarithm values of the two bands) which corrected different bottom types to invert water depth. Following Stumpf et al. and according to Equation (3), we found an alternative exponential solution on the logarithmic ratio of the two bands in inverting the bottom reflectance at 550 nm by rotating the $\ln \left[r_{rs1}\right]-\ln \left[r_{rs2}\right]$ coordinate system. If this ratio condition applies, we would expect that the transformed ratio would approximate the bottom reflectance independently of water depth and needs not be scaled to the actual bottom types (LR-S model):

$$B=a_1\times \exp \left(a_2\times C_i^{\prime }\right)$$

(4)

where $B=r_b$, which is the bottom reflectance at 550 nm, $C_i^{\prime }=\frac{{\left[\ln \left(n\times R_{blue}\right)\right]}^{\prime }}{{\left[\ln \left(n\times R_{green}\right)\right]}^{\prime }}$, ${\left[\ln \left(n\times R_{blue}\right)\right]}^{\prime }$, and ${\left[\ln \left(n\times R_{green}\right)\right]}^{\prime }$ are the logarithmic values of the blue- and green-band subsurface reflectance after rotation, respectively. a₁ and a₂ are determined by the first two items on the right side of Equation (3), $\left(\frac{1}{2g_1}\right)/\left(\frac{1}{2g_1}+\frac{c}{2g_2}\right)$ and $\left(\frac{1}{2g_2}\right)/\left(\frac{1}{2g_1}+\frac{c}{2g_2}\right)$ which can be seen as the rotation transformation. The last term on the right side of Equation (3) can be regarded as the translation transformation. n, is typically set to 10,000 to ensure that the logarithmic value is greater than 1.

2.2. Model Checking Using Hydrolight Simulation Dataset

Hydrolight version 5.3 [31] was used to simulate the propagation of light in clean shallow reef waters. Based on the assumption that the inherent and apparent optical properties are highly similar across oceanic and reef waters (Case-1 phytoplankton dominated water), we only considered one dominant Inherent Optical Property (IOP) of Chl-a [32], which we set at 0.05, 0.1, 0.15 and 0.2 mg/m³, respectively [33,34,35,36]. Please note that the content of the simulation shown in the following is a result at 0.2 mg/m³ of Chl-a (the other three situation results are in the Appendix B, Figure A1, Figure A2, Figure A3). The detailed simulation steps are described in the Appendix B, and the settings for each parameter are shown in

Table A1. Environmental inputs used in the Hydrolight simulations.

Variable	Inputs
Particle phase function	Petzold average particle
Inelastic scattering	Ignore
Chlorophyl a [chl-a](mg/m3)	0.05, 0.1, 0.15, 0.2
B (550 nm): ooid_sand	0.44, 0.49, 0.54, 0.59, 0.64, 0.69, 0.74, 0.79
H: water depth	0.5–20 m, every 0.5 m
λ	400–700 nm, every 10 nm
Sea surface wind speed	5 m/s
Salinity	0.035
Solar zenith angle	30°

.

After simulating the reflectance of different wavelengths in each scenario, we represented the logarithmic value of the blue–green band for the $\ln \left(\mathrm{n}\times R_{blue}\right)-\ln \left(\mathrm{n}\times R_{green}\right)$ coordinate system (Figure 1a). Figure 1b shows a scatter plot of H and $C_i$, which is the ratio of $\ln \left(\mathrm{n}\times R_{blue}\right)-\ln \left(\mathrm{n}\times R_{green}\right)$ for the scenarios. Based on Equation (3), we rotated the $\ln \left(\mathrm{n}\times R_{blue}\right)-\ln \left(\mathrm{n}\times R_{green}\right)$ coordinate system around the center of gravity from –90–90° (i.e., the stipulation that the clockwise rotation is negative). Prior to rotation, $C_i^{\prime }$ and B were arranged regularly, and there was no specific functional relationship (Figure 1d). As the rotation angle was gradually adjusted, there was a significant change in the correlation coefficient of the exponential relationship between them (Figure 1e). The rotation angle at which the relationship had the largest correlation coefficient was selected as the optimal rotation angle (Figure 1c). In this case, Figure 1f shows the relationship between B and $C_i^{\prime }$, which is the optimal exponential correlation.

To evaluate the applicability of our LR-S model, the subsurface reflectance of the blue–green–red–Nir band values were used as the input for the LR-S model to perform the inversion of the bottom reflectance at 550 nm and water depth. The effectiveness of our method was quantitatively checked by comparing the input bottom reflectance B1 and water depth H1 with the inverted bottom reflectance B2 and water depth H2. Figure 2 shows the specific checking workflow.

Figure 3a shows the overall fit between the inverted bottom reflectance and the input values from Hydrolight. We used different colors to display the bottom reflectance under different water depths. In some bias exits, B2 was distributed in all water depth ranges as we input B1 from 0.35 to 0.90, and the overall fit showed high accuracy with an RMSE of 0.06, indicating that the bottom reflectance we inverted was independent of underwater topography. Figure 3b shows that the bathymetric inversion results were not limited by bottom-covering types either, although the accuracy of approximately 20 m was slightly worse. Similarly, with a whole RMSE of 1.12 m, the water depth inversion results were consistent with the input depth of H1. Therefore, the good results of this quantitative checking proved the applicability of our algorithm.

2.3. Workflow

The workflow of the proposed LR-S model is shown in Figure 4. When the model was applied to invert the bottom reflectance, a series of multispectral image preprocessing steps had to be completed. Then, based on the semi-analytical and log-ratio models, the multispectral remote sensing images were used to simultaneously obtain the bottom reflectance and water depth of each self-inferred point (SIP) selected on the corrected imagery according to the spectral characteristics randomly [37] (the specific algorithm of this calculation process is in the Appendix A). With the results of the above steps, the LR-S model was applied to the whole corrected image to invert the bottom reflectance, B, and the water depth, H, over the study area.

3. Case Study

3.1. Study Area, In-Situ Water Depth Data and Benthic Mapping

Midway Island is part of the Hawaiian archipelago, approximately 2100 km northwest of Honolulu in the central Pacific Ocean. Midway is a coral atoll with a circumference of 24 km and a land area of 5 km². The terrain is low and flat. The highest point of the island is 13 m above sea level. The central longitude and latitude of the study area are 28°12′38″ N and 177°21′16″ W. Figure 5a shows the geographical location of Midway Island.

This study used measured water depth data from the NOAA Pacific Island Fisheries Science Center and the Coral Reef Ecosystem Division Pacific Islands Benthic Habitat Mapping Center (ftp://ftp.soest.hawaii.edu/pibhmc/website/data/nwhi/bathymetry/, accessed on 29 January 2021). The bathymetric data were measured from 29 July 2003, to 7 December 2011, and published on 21 December 2011. As mentioned in the metadata files, the measured data were obtained with multibeam soundings, a depth measurement range of 0–200 m, and a sampling interval of 1 m. GPS was used for geo-positioning, with a horizontal positioning accuracy of 25 m and a depth-measurement accuracy of 1 m. Figure 5b shows the distribution of measured depth points within the study area.

We used the University of Queensland Habitat Map (https://github.com/CoralMapping/AllenCoralAtlas, accessed on 29 January 2021) for comparison with the bottom reflectance we inverted. Figure 5c shows this benthic map, which includes coral/algae, microalgal mats, rock, rubble, and sand. Their classification scheme was determined according to machine learning random forest classification followed by an object-based cleaning approach using eco-geomorphological rules and without relying on in situ data, which may create inaccuracies.

3.2. Satellite Images

A WorldView-2 multispectral image over Midway Island acquired on 14 March 2016, was used. The WorldView-2 high-resolution commercial imaging satellite runs in a sun-synchronous orbit at a height of 770 km, which provides a multispectral image with a resolution of 2 m. Figure 6a shows the WorldView-2 original image. In the image selected, cloud coverage was only 0.3%.

A Landsat-8 multispectral image with the spatial resolution of 30 m acquired on February 02, 2016 (Figure 6c) over Midway Island was also used to invert the bottom reflectance and water depth. The image scene over the study case exhibited excellent environmental quality, with little to no cloud cover. In order to make our method universal to all available multispectral remote sensing imagery, we mainly considered four bands from the visible bands to the near-infrared band (WorldView-2: band 2, 3, 5, 7; Landsat-8: band 2–5).

3.3. Preprocessing of the Images

The preprocessing of the WorldView-2 (Figure 6a) and Landsat-8 (Figure 6c) multispectral remote sensing images of Midway Island included radiometric, sun glint, and atmospheric corrections. First, we used radiation correction to eliminate, as far as possible, the difference between the sensor’s measured value and the target’s spectral reflectance caused by the sensor’s own conditions (i.e., atmospheric conditions such as mist, solar position, and angle conditions). Then, we converted the raw digital numbers to the remote sensing reflectance.

3.3.1. Sun Glint Correction

We effectively suppressed the interference of sun glint on sea surface signals through the linear relationship between the visible and near-infrared bands [37]. First of all, we assume that the multispectral image satisfies the following conditions: that the near-infrared band sea surface radiation is very low, and that the near-infrared band sea surface radiation value has only the environmental constant and the sun glint contribution. The mathematical model is as follows:

$${\rho }_{TOC}^{deg}\left(\lambda \right)= {\rho }_{TOC}\left(\lambda \right)-b_{\lambda }\left({\rho }_{NIR}-MIN{\rho }_{NIR}\right)$$

(5)

where ${\rho }_{TOC}^{deg}\left(\lambda \right)$ is the surface reflectance after the sun glint is removed, ${\rho }_{TOC}\left(\lambda \right)$ is the apparent reflectance at the top of the atmosphere, ${\rho }_{NIR}$ is the reflectance in the near-infrared band, $MIN{\rho }_{NIR}$ is the minimum reflectance of the near-infrared band in a given range, $b_{\lambda }$ is the regression coefficient of the near-infrared band and the visible bands in a given range, and λ is the center wavelength.

3.3.2. Atmospheric Correction

In marine remote-sensing, nearly 90% of the signals received by satellite sensors come from the atmosphere. Therefore, in order to achieve more accurate inversion results of bottom reflectance and water properties, it is necessary to perform an accurate atmospheric correction first. The physics-based correction methods by radiative transfer model are usually hard for users to operate practically, which require synchronous measurement of atmospheric aerosol parameters at the imaging time. In this way, some researchers [38,39] proposed the image-based methods which are solely based on remote sensing images and without the dependence of in situ measurement. The dark object subtraction (DOS) method is one of the techniques and has been widely used [8,37,40], which assumes stable dark objects (nearly zero-pixel value) exist, such as the clear optically deep waters.

Based on these considerations, we used the DOS method to eliminate radiation errors due to the atmospheric absorption and scattering. We regarded the spectrum of the optically deep-water pixels of the synchronous MODIS RRS product as the benchmark, wherein the dark objects’ remote-sensing reflectance of the blue, green and red bands during the correction was estimated 0.0060, 0.0020 and 0.0002, respectively. The atmosphere in the study area was assumed to be uniform, then the pixel values of each band in optically deep waters were corrected to this datum. Finally, the sea surface remote sensing reflectance of the optically shallow waters was calculated according to the correction amount in the deep waters. Figure 6b,d shows the preprocessing resulting image of WorldView-2 and Landsat-8, respectively.

3.4. Inversion of Bottom Reflectance and Water Depth

According to Xia et al. [37], we selected a total of 209 SIPs from the WorldView-2 image (Figure 6b) and 181 SIPs from the Landsat-8 image (Figure 6d) and simultaneously obtained the bottom reflectance, B, and water depth, H, of each SIP. The results had a good exponential relationship between the rotated $C_i^{\prime }$ and the inverted bottom reflectance (Figure 7c) which was consistent with the simulated data (Figure 1f). Figure 7a,b corresponded to Figure 1a,b, respectively.

The LR-S model was finally used to invert the bottom reflectance (550 nm) and the water depth of the entire WorldView-2 image. We used the OSU Tidal Prediction software [41] to calculate the tide level corresponding to the imaging time (−0.04 m), and we corrected the water depth inversion results accordingly. Figure 8a,d show the final calculation results. Figure 8b,c showed the local fine-structure characteristics of the underwater terrain, while Figure 8e,f showed the local fine-structure features of the change in bottom reflectance. Based on Figure 8a, deep water was located outside the atoll area and shallow water was located inside this area. The circle lagoon, obtained by inversion, in the southwest of the image corresponded to what was shown in the remote sensing image. The enlarged image in Figure 8c, the contours of the middle reef flats were accurately identified. The distribution of the bottom reflectance in Figure 8d showed clear spatial patterns, which was not as regular as the water depth.

The variation trend in the bottom reflectance from inside the reef to the outside was more complicated. In the atoll and middle island reef areas, the bottom reflectance was relatively homogeneous (generally between 0.02 and 0.2). In contrast, the reflectance of the bottom in shallow water beyond these areas was higher, i.e., between 0.3 and 0.56. The enlarged diagrams (Figure 8e,f) showed that the bottom reflectance in the shallow water area may be high or low. In addition, the maximum inverted water depth at the outer edge of the reef may not reach 30 m in some places due to the bottom types, i.e., section EF we selected was 30 m, which corresponded to a larger sediment reflectivity, while the maximum water depth of section GH was 20 m, which corresponded to a lower sediment reflectivity.

To produce a certain three-dimensional effect from the above results, we used the hillshade tool to create a shaded relief from the bathymetry which were then overlaid with the bottom reflectance map. The overlay effect and the partial magnification maps are shown in Figure 8g–i. The superposition showed the texture structure visually and intuitively, i.e., the blue-striped bulge areas and the gaps between them and the convex point reefs, which had a good stereoscopic effect.

The LR-S model was further used to invert the bottom reflectance and the water depth of the entire Landsat-8 image of Midway Island with similar imaging time using the same process as with the WorldView-2 image. The mapped results from the Landsat-8 image had a coarser spatial resolution but similar gradients of bottom reflectance and water depth as compared to those from the WorldView-2 image (Figure 8; Figure 9). Such results suggest that our method is robust for different satellites.

4. Discussion

4.1. Cross-Checking Using WorldView-2 and Landsat-8 Images

To further check the reliability and robustness of our algorithm, certain samples were selected for a quantitative assessment of the Landsat-8 and WorldView-2 inversion results. We reduced the spatial resolution of the raster data of the bottom reflectance and the water depth inverted from the WorldView-2 and resampled them to the same as Landsat-8 to ensure consistency in space. We then created thousands of random points on the overlapping area of the two data sets and distributed them in different pixels, which meant one sample point at most was positioned in a pixel, and the pixel values were then extracted at the corresponding positions of the two data inversion results. Figure 10a showed the distribution of the sample points while Figure 10b,c provided a scatter density map of the results.

The bottom reflectance at 550 nm and water depth inversion results of the two data sets had high correlation coefficients and both fluctuated near the 1:1 line with a mean deviation of 0.05 and 1.02 m, respectively. There were two clusters of the bottom reflectance between 0.05–0.20 and 0.35–0.50 in (b), indicating that low reflectivity and high reflectivity areas made up most of the Midway Island. The water depth in the range of 5–10 m had the highest density, while in other ranges, the fitting results were slightly scattering.

4.2. Indirect Checking Using In-Situ Water Depth Data

The LR-S model can simultaneously invert the bottom reflectance and water depth, so that the quantitative validation of the inverted water depth can be used to indirectly check the reliability of the bottom reflectance results. When the water depth meets the accuracy, the bottom reflectance is considered to be reasonable. Here, we selected two representative sections (AB and CD) on WorldView-2 imagery with large variations in water depth, as marked in Figure 6b, and compared the inversion data to in-situ data. As shown in Figure 11a,b, the variation trends of the inverted and measured depth were basically the same. In regions where there was no matching validation data, the results also accurately reflected the changes in water depth shallower than 5 m, based on a trend perspective.

Additionally, we generated a series of random points in the range of 5–30 m of the two sections to quantitatively validate the inversion depth. Figure 11c shows a scatter density plot of WorldView-2 with a root mean square error (RMSE) of 1.25 m, which had a high accuracy. In addition, it is worth noting that the positioning error of measured water depth data may slightly affect the accuracy of the result.

4.3. Indication of the Bottom Reflectance for Benthic Habitat Mapping

The benthic habitat mapping in our study is defined by us as “The use of multispectral remote sensing imagery to indirectly obtain the dominant coverage types (e.g., coral/algal, sand, rubble) distributions on the shallow seafloor areas which are different from their surroundings in terms of bottom reflectance characteristics, when observed at particular spatial and temporal scales” [42,43]. For example, coral habitat is any hard bottom area supporting living corals and/or algae, with a dark signal (lower reflectance on the whole, typically at 550 nm) and potentially occurring in the sand class; sand includes any soft-bottom area dominated by fine unconsolidated sediments, with bright signal characteristics (higher reflectance on the whole, typically at 550 nm) [44].

Figure 12 visualizes the assessment result between our inverted bottom reflectance and the benthic map of the Allen Coral Atlas for each type. According to the Atlas in Figure 5c, there are three dominant types (coral/algae: 28.43%, rubble: 22.84%, and sand: 44.95%) and one low coverage type of Microalgal Mats (3.41%). The area of the other type of rock in this atlas corresponding to the remote sensing images were covered by broken waves which we masked in the pre-processing, comprising the remaining 0.21% (1.85% before masking). Therefore, the bottom reflectance of Sand, Coral/Algae, Microalgal Mats and Rubble in Figure 12 were distributed normally, while the bottom reflectance distribution of Rock cannot represent the true shape. Although there was a small proportion part outside the 80% confidence interval, sand had the highest reflectance peak range, followed by Microalgal Mats and rubble, and coral/algae was the lowest, which was consistent with empirical knowledge.

Due to the coverage being nearly zero, there may be larger errors in the classification of rock and Microalgal Mats, which had a scattered distribution in Allen Atlas and did not have sufficient statistical conditions. The classification of the Allen Atlas itself may create some inaccuracy as the empirical method they used was not entirely based on in situ data. However, this would not make a substantial difference to our result because we only use this atlas to evaluate the indicative role of bottom reflectance for benthic habitat mapping in this section.

From Figure 11b, the bottom reflectance between 0.05–0.20 and 0.35–0.50 of the two inversion results was the most concentrated, which corresponded to coral/algae and sand in Figure 12, respectively, while the bottom reflectance in the middle range between 0.20–0.35 corresponded to Rubble or Microalgal Mats accordingly. These all showed that the quantitative bottom reflectance we inverted would greatly contribute to the determination of sediment types, which has great potential and application value in benthic classification.

4.4. Inversion Ranges under Different Bottom Reflectance

Within a small geographic region in the study area, the maximum inversion depth could not be consistent. As we have seen, it could only reach 20 m in the northernmost part of the island which indicated that our vertical detection range would be restricted under certain conditions. Thus, to evaluate the inversion ranges in vertical direction under different bottom reflectance, we selected the EF and GH sections in Figure 8a, with significantly different variation ranges. Figure 13a comprehensively showed the inversion ranges in the verticality corresponding to the respective bottom reflectance B across the two sections. Here, EF’s bottom reflectance was generally high, and the range that can be inverted in the vertical direction was large, while the bottom reflectance of GH was lower on the whole, and the range that can be inverted was small. As we can see, the red line broke at minimum B which was almost zero (after transect 400) while the blue line can reach a deeper value. Why did this phenomenon occur?

From the subsurface reflectance changes of the blue bands (has the strongest penetration) across the two sections in Figure 13b, GH contained much less reflected energy from the substrate with a lower bottom reflectance which was almost completely absorbed or scattered and cannot reach the subsurface, especially after transect 400. Accordingly, it was impossible to perform a large inversion range in such areas. By contrast, the subsurface reflectance of EF remained higher such that we can obtain a deeper range. Thus, we used the dotted line in Figure 13b to define an approximate blue band threshold, below which the inversion range was beyond our detection. Only the part above the dotted line is the applicable and reliable range for the inversion of B and H.

5. Conclusions

We developed a novel method for quantitatively inverting the bottom reflectance of oceanic reefs without a priori knowledge, by integrating a semi-analytical model and a log-ratio model. Through linking different pixels in the same image and utilizing the strong linear relationship between their water depths and the spectral related parameters, a physics-based LR-S model between the bottom and subsurface reflectance was established. Based on a Hydrolight simulation spectrum, which was the result after inputting bottom reflectance B1, water depth H1 and other parameters, we inverted B2, H2, which both correlated well with the input values, indicating that the application of the bottom reflectance inversion method we proposed is feasible, robust, and reliable. In addition, the two interfering variables we obtained, i.e., bottom reflectance and water depth, were separated successfully in the inversion process. Future work that collect the field-based bottom reflectance spectra, is required for direct validation.

In the case study of Midway Island, the bottom reflectance mapping we inverted showed clear spatial patterns and the water depth mapping conformed to the actual situation. We conducted a cross-checking for this method using Landsat-8, whose imaging time is similar to that of WorldView-2. The results showed that the inversion results of the two datasets were highly consistent and the mean deviation between the bottom reflectance was 0.05, which were highly convincing and indicated that we obtained reasonable and fine-resolution inversion results of the bottom reflectance. The water depth inversion results of WorldView-2 correlated well with the in-situ data, which indirectly indicated the reliability of the inversion results of the bottom reflectance and the applicability of the LR-S model we developed. The bottom coverage distributions in Figure 8d and Figure 9d was basically consistent with the two clusters in Figure 11b and the distribution in Figure 5c. Additionally, according to Figure 8; Figure 9, in deeper waters around the atoll, healthy corals, seagrass, or algae may be located, which had a reflectance equal to the lower bottom reflectance in the study area. The bottom in the middle island reef area may be bleached coral or sand, which coincided with the higher reflectance shown in Figure 8d.

From the textural structure in Figure 8h, the reflectance of the blue striped bulge area was low, which we predicted as a typical growth zone of coral reefs. The yellow and red parts in their growth gaps were sand with a high reflectance. In Figure 8i, the bottom reflectance at the water depth of approximately 10 m was low, in which the bottom coverage in the flat area might correspond to small seagrass or algae; the convex part might be submarine coral reefs, while the bottom of the area around 7 m may be covered by sand with a high reflectance. The histogram of each bottom type in Figure 12 corresponded well with the benthic map of Allen Coral Atlas. These all illustrated that the quantitative bottom reflectance we inverted is an important factor in determining bottom types, which has great potential in benthic mapping. We also found that the inversion ranges in vertical direction within a small region may vary greatly under different bottom reflectance. The higher the bottom reflectance was, the much the reflected energy from the bottom would be contained, then the higher the subsurface reflectance would remain, finally the deeper range we would obtain.

The physics-based method we proposed is the first to quantitatively invert the bottom reflectance using multispectral images without the dependence of in situ data, which can be used to establish a unified bottom index on a large regional scale (even the global scale) to understand the composition of bottom types. Specifically, it can be used to quantitatively compare the bottom reflectance among different research areas or image scenes. In addition, this method weakens the influence of water depth by simultaneously obtaining water depth and the bottom reflectance. Consequently, it is helpful to more reliably map the bottom reflectance, while not interfering with water depth. Moreover, the method is robust for different remote sensing images with various spatial resolutions. With the increasing availability of medium- and high-resolution remote sensing data, our method holds promise in detecting oceanic island reef bottoms, benthic mapping, and the early forecast of the coral reef bleaching because of the important indication of the quantitative bottom reflectance for bottom types. Our physics-based method can be transferred to other clear optically shallow regions, and the inverted bottom reflectance can provide essential information of benthic types, which is of great importance for environmental conservation and sustainability.