Next Article in Journal
Hyperspectral Empirical Absolute Calibration Model Using Libya 4 Pseudo Invariant Calibration Site
Next Article in Special Issue
Dynamics of Vegetation Greenness and Its Response to Climate Change in Xinjiang over the Past Two Decades
Previous Article in Journal
Managing Agricultural Water Considering Water Allocation Priority Based on Remote Sensing Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 8
10.3390/rs13081535
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Mapping the Forest Canopy Height in Northern China by Synergizing ICESat-2 with Sentinel-2 Using a Stacking Algorithm

by
Fugen Jiang
1,2,3,
Feng Zhao
4,
Kaisen Ma
1,2,3,
Dongsheng Li
5 and
Hua Sun
1,2,3,*
1
Research Center of Forestry Remote Sensing and Information Engineering, Central South University of Forestry and Technology, Changsha 410004, China
2
Key Laboratory of Forestry Remote Sensing Based Big Data and Ecological Security for Hunan Province, Changsha 410004, China
3
Key Laboratory of State Forestry Administration on Forest Resources Management and Monitoring in Southern Area, Changsha 410004, China
4
State Key Laboratory of Estuarine and Coastal Research, Institute of Eco-Chongming, East China Normal University, Shanghai 200241, China
5
Hebei Academy of Forestry and Grassland Investigation and Planning, Shijiazhuang 050051, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(8), 1535; https://doi.org/10.3390/rs13081535
Submission received: 9 March 2021 / Revised: 13 April 2021 / Accepted: 13 April 2021 / Published: 15 April 2021
(This article belongs to the Special Issue Applications of Remote Sensing in Earth Observation and Geo-Information Science)
Browse Figures
Versions Notes

Abstract

:
The forest canopy height (FCH) plays a critical role in forest quality evaluation and resource management. The accurate and rapid estimation and mapping of the regional forest canopy height is crucial for understanding vegetation growth processes and the internal structure of the ecosystem. A stacking algorithm consisting of multiple linear regression (MLR), support vector machine (SVM), k-nearest neighbor (kNN), and random forest (RF) was used in this paper and demonstrated optimal performance in predicting the forest canopy height by synergizing Sentinel-2 images acquired from the cloud-based computation platform Google Earth Engine (GEE) with data from ICESat-2 (Ice, Cloud, and Land Elevation Satellite-2). This research was conducted to achieve continuous mapping of the canopy height of plantations in Saihanba Mechanical Forest Plantation, which is located in Chengde City, northern Hebei province, China. The results show that stacking achieved the best prediction accuracy for the forest canopy height, with an R2 of 0.77 and a root mean square error (RMSE) of 1.96 m. Compared with MLR, SVM, kNN, and RF, the RMSE obtained by stacking was reduced by 25.2%, 24.9%, 22.8%, and 18.7%, respectively. Since Sentinel-2 images and ICESat-2 data are publicly available, this opens the door for the accurate mapping of the continuous distribution of the forest canopy height globally in the future.

Graphical Abstract

1. Introduction

The forest canopy height plays a significant role in vegetation health assessment [1,2], and is also critical for deriving several key biophysical parameters, such as the aboveground biomass (AGB), carbon storage, biodiversity, vegetation photosynthesis, carbon cycle, and global climate change [3,4,5]. Obtaining accurate, large-scale, and multitemporal forest canopy height information can provide policymakers with scientific information on deforestation, forest degradation, and forest quality [6].
The application of remote sensing technology in forest surveying has greatly improved the efficiency of forest management [7]. Optical remote sensing, synthetic aperture radar (SAR), and light detection and ranging (LiDAR) data have been widely used in land change and vegetation cover mapping [8,9,10,11,12,13]. Among these, LiDAR has proved to be the most accurate in estimating forest vertical structure parameters, with its unique advantage of penetrating through the upper forest canopy to characterize the understory and bare ground [4,12,14].
The advanced topographic laser altimeter system (ATLAS) carried by the Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2) is one of the latest space-borne LiDAR systems, and was launched on September 15, 2018. It has a high repetition rate and high sensitivity [15,16,17]. ICESat-2/ATLAS adopts micropulse multibeam photon counting LiDAR (PCL) technology and represented the first time that this technology had been applied to a space-borne platform [17]. A more sensitive single photon detector was used in ATLAS, which has higher pulse repetition rate, and can obtain photon point cloud data with a smaller spot and higher density, so as to achieve more precise surface 3D information extraction [18]. ICESat-2 can provide forest vertical structure parameters and obtain global forest dynamic change information, and it has the potential to reveal the current situation and change law of the vegetation canopy height and biomass in large regions [15,19].
Coupling spatially contiguous optical data with LiDAR-derived vegetation attributes to map the spatial distribution of the forest canopy height is a widely used approach now [17,19]. Optical satellite technologies such as those of MODIS [20], Hyperion [21], Landsat [22], Sentinel [23], and Worldview [24] can provide multiple spatial resolution and multispectral data and obtain surface feature information on different bands [8]. Compared with other optical data, Sentinel-2 data have a moderate spatial resolution, and because the red-edge bands carried by its multispectral imager (MSI) sensor are more sensitive to vegetation growth, it can provide more accurate information on land changes and vegetation growth [25].
Google Earth Engine (GEE) is a powerful cloud-based geospatial processing platform that can be used for large-scale terrestrial ecosystem monitoring [17,26]. GEE archives a large amount of remote sensing data for public use, and users are able to apply their algorithms directly to the data. Due to its high efficiency, GEE has been widely used by researchers for land cover and land use change (LCLUC) assessment, disaster management, and forest monitoring [27,28,29].
Since space-borne LiDAR data are spatially discontinuous, optical remote sensing data need to be employed for extrapolation to map the forest canopy height [17,19]. Parametric and nonparametric models have been used for extrapolation purposes [17]. Parametric models (e.g., multiple linear regression (MLR)) are intuitive and easy to understand, and they can directly build the relationship between remote sensing variables and forest parameters such as the AGB and leaf area index (LAI) [30,31]. However, many parameters in parametric models are difficult to obtain from the forest inventory. In addition, parametric models are not able to explain nonlinear relationships among the parameters well [32,33]. Compared with parametric models, nonparametric models are flexible and require no model assumptions or a specific sample distribution (e.g., normal distribution) [34]. In addition, nonparametric models can ignore the collinearity between remote sensing variables used to estimate forest parameters, which greatly improves the utilization of remote sensing information and the efficiency of the model [32,35]. Commonly used nonparametric methods include support vector machine (SVM) [36], k-nearest neighbor (kNN) [37], and random forest (RF) [38]. The kernel function is the inner product of the mapping relationship, which can be used to increase the feature dimension for better classification [39]. Support vector machine (SVM) has many kernel functions (e.g., radial basis function (RBF), Gaussian, and the exponential kernel [40,41]) for different classifications and regressions. Compared with the traditional regression model, SVM is more robust and can eliminate partial overfitting [34]. kNN determines the attributes of the samples to be tested by sorting the spectral distances between the samples and the nearest k samples. kNN does not need parameter estimation and training, and it is easy to understand and implement [36]. Random forest is a nonparametric ensemble learning method that effectively processes large data sets. Multiple decision trees can be quickly created by RF for classification and regression [35,38]. Nonparametric methods have been widely used in estimating vegetation parameters [34,35,36]. Compared with individual models, ensemble learning is able to combine multiple base models that are functionally independent classifiers or regressors to obtain a better and more comprehensive prediction model [7,38]. Even if one base learner gives a wrong prediction, other base models can correct and improve it [42]. As the representative of ensemble learning, the stacking algorithm is able to train a model to combine other base models. Stacking can integrate the advantages of each individual base model to establish a prediction model with a better estimation effect and applicability [43]. Li et al. [44] mapped the growing stem volume (GSV) of plantations in northeast China successfully using the stacking approach and achieved satisfactory estimation results. In addition, the algorithm has also been applied to predict soil organic matter [45].
This study aimed to develop a stacking approach for estimating and mapping the forest canopy height in northern China with satisfactory accuracy. Specifically, this study combined ICESat-2 data with synthetic Sentinel-2 images obtained from GEE for developing of the stacking, and the derived forest heights were validated with ground-truth data collected in Saihanba, Heibei, China.

2. Materials and Methods

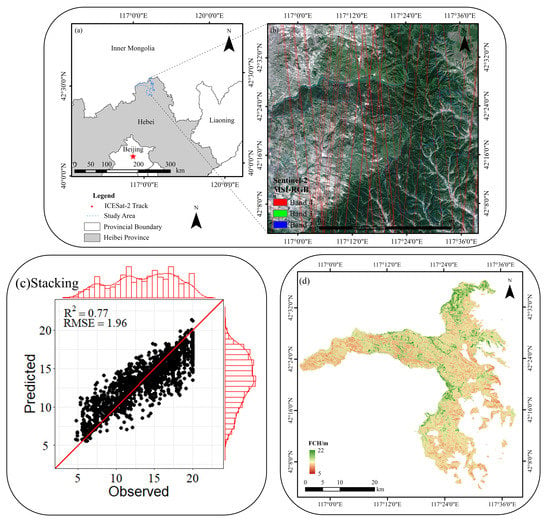
2.1. Study Area

The Saihanba Mechanical Forest Plantation is located in Chengde City, northern Hebei province, China (116°51′~117°39′ E, 42°02′~42°36′ N) (Figure 1) and covers an area of 933.33 km2, with an elevation ranging from 1010 to 1940 m. The study area is characterized by a temperate continental monsoon climate, with a minimum temperature of −43.2 °C and an average annual snow cover of 7 months. The annual mean precipitation is about 490 mm, with an average annual frost-free period of 68 days. The Saihanba forest farm was established in 1962, and the total volume of trees has reached 10.12 million m3 currently. The dominant tree species are larch (Larix ologensis), Scots pine (Pinus sylvestris), birch (Betula platyphylla Suk), and spruce (Picea asperata Mast).

2.2. Measurement of the Forest Canopy Height in Saihanba

The forest management inventory (FMI), which is carried out every ten years in China, plays a key role in forest resources monitoring and evaluation. A forest resource database composed of irregular blocks was established and is updated once a year in the FMI to guide the management of forests [26,46]. The database was updated in 2017, including land type, block area, forest canopy height, and tree species, and this information was analyzed to obtain the forest canopy information of Saihanba.
In our study, 5404 sample plots composed of seven tree species were selected from Saihanba forest experiment sites (Figure 2). As the most widely distributed tree species, larch accounted for 56.2% of all sample plots. Its canopy height ranged from 3.7 m to 20.0 m, and the mean, standard deviation, and coefficient of variation were 15.39 m, 3.69 m, and 23.9%, respectively. The canopy height of spruce had the largest coefficient of variation of all the tree species, while the mean value and standard deviation of oak was the lowest (Table 1).

2.3. ICESat-2 ATLAS Data and Processing

The ICESat-2 carries an advanced terrain laser altimeter system (ATLAS), which emits three pairs of beams. The distance between each pair of beams is about 3.3 km, and the distance between two trajectories in the beam is 90 m. Three pairs of laser beams represent six ground trajectories, and the corresponding data numbers from left to right are, respectively, Ground Track 1 Left (GT1L) to Ground Track 3 Right (GT3R) [14,19,47,48].
The ICESat-2 products include three levels, from ATL01 to ATL21, and the ATL08 data (level 3) covering the whole study area from 5 November 2018 to 8 December 2019 were downloaded from the National Ice and Snow Data Center (NSIDC) (https://nsidc.org/data/ATL08/ accessed on 8 March 2021) (Figure 3a). The ATL08 product directly provides data on the terrain, height metrics, and apparent surface reflectance (ASR) (Table 2) in fixed 100 m data segments along the track, with a diameter of 17 m (Figure 3) [23]. The height metrics include minimum height, mean height, median height, maximum height, and 10 height profile quantiles, which can be used as variables for forest height modeling and estimation, together with ASR.
Terrain, height metrics, and apparent surface reflectance attributes from the ATL08 product for our study area were extracted. The canopy height was calculated from 98% of all individual relative canopy heights in the region. As a PCL system, ATL08 is easily affected by the noise from the atmosphere and the sun background. Therefore, ATL08 was denoised before processing and obtaining the vegetation products [49]. Segments of less than 50 signal photons were filtered out, as they did not characterize the ground surface accurately. To make full use of available ATL08, the differential, regressive, and Gaussian adaptive nearest neighbor (DRAGANN) methods were developed to identify and remove noise photons from the histogram of photon point clouds [49,50]. In addition, the segments with an average canopy height greater than 50 m and less than 2 m were excluded as invalid values.
Table 3 shows the canopy height distribution for all 5404 segments covering the study area. The canopy height of the segments ranged from 15 to 20 m, accounting for 48.5% of all segments. By contrast, the canopy height for all the segments varied broadly from 4.26 to 26.41 m, with a mean, standard deviation, and coefficient of variation of 15.11 m, 3.62 m, and 23.9%, respectively.

2.4. Sentinel-2 Image Preprocessing and Spectral Variable Calculation

While ICESat-2 cannot provide wall-to-wall coverage, combining it with continuous remote sensing data, such as those from Sentinel-2, proved to be an effective method with which to map the forest canopy heights [17]. Sentinel-2 was launched in June 2015, and it is now widely used in forest parameter estimation and land cover mapping, as the red-edge bands are sensitive to the chlorophyll of vegetation leaves [23]. Level-2A Sentinel-2 images in the growing season (June–September) from 2018 to 2019 were downloaded with the cloud-based computation platform Google Earth Engine (GEE, https://code.earthengine.google.com/ accessed on 8 March 2021). The Sentinel-2 images obtained were a Level-2A product; they were atmospherically corrected by the Sen2Cor module, and the pixels were transformed to account for surface reflectance. The quality assessment band (QA60) was used for cloud masking [26]. To obtain more stable and higher resolution pixel values, the visible bands (red, green, blue, and near-infrared), with a resolution of 10 m, and three red-edge bands (RedEdge 1–3), with a resolution of 20 m, were selected and applied to obtain a median image composition. A total of eight vegetation indices, including five common vegetation indices and three red-edge vegetation indices, were extracted as spectral features to establish a link between ICESat-2 and the mapping (Table 4).

2.5. Model Development and Assessment

2.5.1. Parametric and Nonparametric Models

Parametric and nonparametric models are commonly used for forest parameter estimation [30,31,32,35]. Parametric models, such as multiple linear regression (MLR), are easy to implement and can describe the quantitative relationship between multiple variables and the forest canopy height. However, under complex forest conditions, the relationship between remote sensing variables and the forest canopy height may be complex [32]. Nonparametric models have the potential to estimate forest parameters with satisfactory accuracy and have been proved to be effective [35]. This study used support vector machine (SVM), k-nearest neighbor (kNN), and random forest (RF) to estimate forest height compared with MLR. In addition, a stacking algorithm composed of these four models was established to explore its potential in estimating the forest canopy height.
MLR assumes that there is a highly linear relationship between the dependent variable and independent variables; it can measure the effect of multiple variables on the prediction, and it is a commonly used parametric model [30]. It is more effective and practical to predict or estimate the dependent variable with a combination of multiple independent variables than by using only one independent variable [31]. The general expression of a multiple linear regression equation is shown in Equation (1).
  Y = β 1   X 1 + β 2   X 2 + β 3   X 3 + … + β n   X n + C
where Y is the dependent variable,   X 1 ,   X 2 ,   X 3 … X n is the independent variable, β 1 , β 2 ,   β 3 β n is the regression coefficient, and C is a constant.
SVM can achieve good prediction performance, even if there are few samples available. The nonlinear kernel function can transform the input data into high-dimensional feature space and reduce the error and complexity of the model [36,40,41]. The radial basis function, Gaussian function, and exponential kernel function were established and compared, and the kernel function with the minimum estimation error was determined. The “tune.svm” function in R (package “e1071” [55]) can be used to set the initial values of the penalty coefficient (cost) and kernel function parameter (gamma) (usually 10−3–103), and then the value with the minimum error rate is selected as the optimal parameter [34].
The kNN algorithm searches the k samples nearest to the sample plot to be predicted by spectral distance, and then uses the specific prediction rules and the attributes of the selected samples to predict the sample plot to be predicted [37]. Samples with a normal distribution are not required in kNN, making it flexible, and it is widely used in estimating forest parameters and biodiversity mapping. The distance measurement, k value, and prediction rules can strongly affect the estimation results [36]. In Saihanba, the Euclidean distance and reciprocal weighting of the distance method were used to predict the forest canopy height (Equation (2)). The k value was set from 1 to 50, and the number of samples with the minimum estimation error was determined.
F C H p = ∑ j = 1 k ( 1 d p j ) × y j ∑ j = 1 k 1 d p j
where F C H p   denotes the predicted FCH at the pixel P, y j   denotes the FCH observation corresponding to the jth sample plot, d p j is the spectral distance from the pixel P to the jth sample plot, and k denotes the optimal number of sample plots.
RF is a widely used nonparametric algorithm in land classification and forest parameter estimation because it is robust, relatively easy to understand, and insensitive to noise data [38]. In addition, it is an ensemble learning method; it constructs a large number of regression trees for the prediction. The number of regression trees (ntree, with a default value of 500) and the number of nodes (mtry, within the number of input variables) are the basic parameters of random forests. The package “randomForest” [56] in R was used for the RF process.

2.5.2. The Stacking Algorithm

The stacking algorithm combines the advantages of the base models, which can greatly improve the prediction effect [44]. First, stacking used the base models to combine training samples to build its own prediction models; then, all the prediction results were set as independent variables to conduct new joint modeling. Stacking generalizes the output of all base models, which can significantly improve the prediction accuracy and reduce the overall error.
In Saihanba, a stacking algorithm consisting of MLR, SVM, kNN, and RF was developed to estimate and map the forest canopy height (Figure 4). The four base models were also used for a direct comparison.

2.5.3. Model Assessment

The ICESat-2 segments were randomly divided into two groups: 70% (training set, n = 3782) for model training and 30% (testing set, n = 1622) for independent validation. The coefficient of determination (R2) and the RMSE [57] were calculated to evaluate the model performance with the testing set.
  R 2 = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ¯ ) 2
RMSE = ∑ i = 1 n ( y ^ i − y i ) 2 n
where y i is the observed value, y ^ i   is the predicted value based on the models, y ¯ is the mean of all the observed values, and n is the sample size. All of the models and calculations were carried out using R 4.0.3 software.

3. Results

3.1. Forest Canopy Height Estimation Models with ICESat-2

All the parameters were significantly and positively correlated with the forest canopy height (p < 0.001) (Table 5). Among them, the 98th percentile height had the highest correlation coefficient of 0.71.
The Pearson correlation coefficient was used to detect linear relationships between the variables and forest height. However, the relationship between the variables and height is not always simply linear in dense forest situations. To add more variable evaluation methods, importance evaluation based on random forest was added to explore the nonlinear relationship between ASR, height metrics, and the measured forest canopy height. The random forest algorithm was used to evaluate the importance of all variables, and the importance ranking was obtained, as shown in Figure 5. The 98th percentile height had the highest importance, while the minimum had the lowest.
The performances of MLR, SVM, kNN, and RF were similar. Stacking achieved the highest fitting and the lowest error, and the RMSE from the stacking model was reduced by 25.2%, 24.9%, 22.8%, and 18.7% compared with each individual model. Figure 6 shows the forest canopy height values predicted by the five models versus the observed values. There were different degrees of overestimation and underestimation when predicting the forest canopy height in Saihanba. However, compared with the other models, stacking greatly reduced overestimation and underestimation, achieving the best fit. The residuals obtained by stacking tended to be randomly distributed.

3.2. ICESat-2 Derived Estimation for Sentinel-2

The importance of variables obtained from the RF model showed that ARVI contributed the most to the model, followed by RECI and NDVI (Figure 7a). The least important variable in the model was the enhanced vegetation index (EVI). The variables were selected with the random forest algorithm based on importance ranking, and the final combination of variables was used to map the forest canopy height continuously, combined with the stacking algorithm. The spatial pattern of the forest canopy height predicted by stacking was highly consistent with those from ICESat-2 (Figure 7b). By extracting continuous optical features from Sentinel-2 and combining them with stacking, the ICESat-2 derived forest canopy height could be predicted with satisfactory accuracy. The R2 and RMSE of the estimation model were 0.92 and 1.37 m, respectively (Figure 7b).

3.3. Discontinuous and Continuous Mapping

ICESat-2 can provide fixed spacing footprints for estimating the forest canopy height with satisfactory accuracy. However, discontinuous footprints are limited for predicting a comprehensive spatial distribution (Figure 8a). The Sentinel-2 images, which were obtained in the growing season of the vegetation, were used as the medium to extract continuous optical variables and were combined with stacking to map the forest canopy height distribution of Saihanba (Figure 8b).
Most of the larger forest canopy height prediction values were distributed in the northeast and south, while the values in the central region were relatively small. The minimum forest canopy height values were distributed in the western part of the region (Figure 8). The spatial pattern of the predicted forest canopy height followed the actual distribution in Saihanba.

4. Discussion

4.1. ICESat-2 Metrics for Canopy Height Estimation

Height metrics extracted from ICESat-2 ATL08 are crucial for improving the efficiency of the stacking model and achieving high-precision canopy height estimation [17,33]. However, ICESat-2 can provide only a limited number of height metrics, and thus all variables need to be employed in the stacking model. Our results showed that the height metrics and ASR extracted from ICESat-2 were closely related to the forest canopy height. The lowest RMSE was achieved by using these variables together with the stacking model. Although the correlation between the ASR, minimum height, and forest canopy height were also significant (p < 0.001), the correlation coefficients were less than 0.1. To verify the effectiveness of these two variables for estimating the forest canopy height, the rest of the variables (excluding the ASR and minimum height) were used to established models to estimate the forest canopy height. The results showed that stacking still achieved the best fitting, and the smallest RMSE. Compared with MLR, SVM, kNN, and RF, the RMSE of stacking was reduced by 20.1%, 21.0%, 20.4%, and 18.3%, respectively. However, after excluding the ASR and minimum height, the RMSE of all models increased sharply. By contrast, the RMSE of stacking increased by 8.4%, indicating that the two variables significantly improved the estimation of the forest canopy height.
In addition, Narine et al. [14] used stepwise regression combined with the collinear elimination method to select variables from all height metrics for AGB estimation and obtained satisfactory accuracy. The method was also used in Saihanba, and the RMSE of the linear variable selection method was 10.9% higher than the results in Table 5, although the best model was still stacking. The height metrics provided by ATL08 were mainly percentile values of canopy height, which may lead to collinearity among variables. In complex forest conditions, the relationship between variables and forest parameters is not simply linear, so collinearity may not be crucial for nonparametric models with a higher estimation accuracy [31]. However, due to the limited number of variables and high correlation, modeling with all the variables extracted from ATL08 did not lead to redundancy and reduced the estimation efficiency.

4.2. Uncertainty, Limitations, and Suggestions

The accuracy of modeling of the forest canopy height is influenced by several factors, such as the topographic relief, tree species, and canopy cover [7,24,26]. Firstly, with the increase of the forest canopy cover, a limited number of photons can reach the ground and be reflected back to the sensor, thus limiting the application of ICESat-2 in forests with high canopy cover [18]. To reduce the uncertainty associated with high canopy cover, footprints with few photons were excluded from the forest canopy height modeling. Second, the forest canopy height model may vary from one species to another.
Out results showed that the poplar (n = 17), Chinese pine (n = 3), and spruce (n = 23) had a small number of samples in the testing set, and the RMSEs were 1.44, 0.45, and 2.41 m, respectively. Larch and birch accounted for the largest number of samples, with RMSEs of 1.96 and 1.95 m, respectively, which was reasonable given the overall estimation accuracy (Figure 9). However, oak had the largest estimation error. Similar to spruce, the accuracy of oak was limited due to the large variation coefficients (33.6% and 26.4%) of the samples.
It is also worth noting that ground-truth data were not collected in the same season and year as the ICESat-2 data. In our study, the ground-truth forest canopy height was measured in 2017, while the ICESat-2 data covering Saihanba was acquired between November 2018 and December 2019. This mismatch between ground-truth data collection and satellite data acquisition may have affected the forest canopy modeling.
The ICESat-2 data does not provide wall-to-wall spatial coverage [14]. Comprehensive mapping of the forest canopy height requires optical data for extrapolation [18]. As a powerful cloud platform, GEE can provide a variety of time series data, such as those from Landsat, Sentinel, and MODIS, to synthesize more stable median images after cloud masking [27]. Combining ICESat-2 with continuous coverage optical images has become an effective method to obtain a high-precision forest canopy height [18,19]. In addition, the Global Ecosystem Dynamics Investigation (GEDI) can provide vertical canopy information between 52°N and S latitudes, which adds another source of LiDAR data [19,58]. Integrating ICESat-2, GEDI, and LiDAR with other forms of optical data, as well as environmental variables, and using machine learning algorithms to estimate the forest canopy height, may have significant potential in the future [59,60,61,62,63,64,65].

5. Conclusions

The accurate estimation of the forest canopy height is of great significance for assessing forest health and terrestrial ecosystem dynamics. In this study, a stacking algorithm consisting of MLR, SVM, kNN, and RF was developed to map the spatial pattern of the forest canopy height in the Saihanba forest experiment site in northern China by coupling the ICESat-2 and synthesized Sentinel-2 time series imagery. The results demonstrated that: (1) the canopy height parameters extracted from ICESat-2 were highly correlated with the field measurements. The correlation between the height metrics and the measured forest canopy height was higher than that of ASR, the 98th percentile height achieved the best correlation (R = 0.71), and (2) compared to individual algorithms (MLR, SVM, kNN, and RF), the stacking algorithm was able to reduce the RMSE by 25.2%, 24.9%, 22.8%, and 18.7%, respectively. To conclude, by combining ICESat-2 and continuous Sentinel-2 images, the forest canopy heights retrieved from the stacking algorithm were more consistent with the actual distribution of forest canopy heights derived from each individual algorithm, suggesting that our stacking algorithm can effectively estimate and map the spatial distribution of the forest canopy height and provide a reference for forest dynamic change monitoring and forest management.

Author Contributions

All authors read the manuscript; conceptualization and methodology, H.S. and F.Z.; validation, F.J. and F.Z.; formal analysis, F.J.; investigation, F.J., D.L., and H.S.; draft, F.J., H.S., and K.M.; supervision, H.S.; review, editing, and revision, F.Z. and K.M.; funding acquisition, H.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the project of the National Natural Science Foundation of China, grant number 31971578; Scientific Research Fund of Hunan Provincial Education Department, grant number 17A225; National Bureau to Combat Desertification, State Forestry Administration of China, grant number 101-9899; and the Forestry Administration of Hunan Province, grant number XLK201986.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
  2. Hayashi, M.; Saigusa, N.; Oguma, H.; Yamagata, Y. Forest canopy height estimation using ICESat/GLAS data and error factor analysis in Hokkaido, Japan. ISPRS J. Photogramm. Remote Sens. 2013, 81, 12–18. [Google Scholar] [CrossRef]
  3. Zeng, Z.; Piao, S.; Li, L.Z.X.; Zhou, L.; Ciais, P.; Wang, T.; Li, Y.; Lian, X.; Wood, E.F.; Friedlingstein, P.; et al. Climate mitigation from vegetation biophysical feedbacks during the past three decades. Nat. Clim. Chang. 2017, 7, 432–436. [Google Scholar] [CrossRef]
  4. Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote sensing of the terrestrial carbon cycle: A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
  5. Vicente-Serrano, S.M.; Camarero, J.J.; Olano, J.M.; Martín-Hernández, N.; Peña-Gallardo, M.; Tomás-Burguera, M.; Gazol, A.; Azorin-Molina, C.; Bhuyan, U.; El Kenawy, A. Diverse relationships between forest growth and the Normalized Difference Vegetation Index at a global scale. Remote Sens. Environ. 2016, 187, 14–29. [Google Scholar] [CrossRef] [Green Version]
  6. Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Espirito-Santo, F.D.B.; Hunter, M.O.; De Oliveira, R. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
  7. Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2014, 9, 63–105. [Google Scholar] [CrossRef]
  8. Gleason, C.J.; Im, J. A Review of Remote Sensing of Forest Biomass and Biofuel: Options for Small-Area Applications. GISci. Remote Sens. 2011, 48, 141–170. [Google Scholar] [CrossRef]
  9. Myneni, R.; Maggion, S.; Iaquinta, J.; Privette, J.; Gobron, N.; Pinty, B.; Kimes, D.; Verstraete, M.; Williams, D. Optical remote sensing of vegetation: Modeling, caveats, and algorithms. Remote Sens. Environ. 1995, 51, 169–188. [Google Scholar] [CrossRef]
  10. Cutler, M.; Boyd, D.; Foody, G.; Vetrivel, A. Estimating tropical forest biomass with a combination of SAR image texture and Landsat TM data: An assessment of predictions between regions. ISPRS J. Photogramm. Remote Sens. 2012, 70, 66–77. [Google Scholar] [CrossRef] [Green Version]
  11. Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random forest wetland classification using ALOS-2 L-band, RADARSAT-2 C-band, and TerraSAR-X imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
  12. Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. Earth Environ. 2003, 27, 88–106. [Google Scholar] [CrossRef] [Green Version]
  13. Vierling, K.T.; Vierling, L.A.; Gould, W.A.; Martinuzzi, S.; Clawges, R.M. Lidar: Shedding new light on habitat characterization and modeling. Front. Ecol. Environ. 2008, 6, 90–98. [Google Scholar] [CrossRef] [Green Version]
  14. Narine, L.L.; Popescu, S.C.; Malambo, L. Synergy of ICESat-2 and Landsat for Mapping Forest Aboveground Biomass with Deep Learning. Remote Sens. 2019, 11, 1503. [Google Scholar] [CrossRef]
  15. Sun, T.; Qi, J.; Huang, H. Discovering forest height changes based on spaceborne lidar data of ICESat-1 in 2005 and ICESat-2 in 2019: A case study in the Beijing-Tianjin-Hebei region of China. For. Ecosyst. 2020, 7, 1–12. [Google Scholar] [CrossRef]
  16. Neuenschwander, A.L.; Magruder, L.A. Canopy and Terrain Height Retrievals with ICESat-2: A First Look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef] [Green Version]
  17. Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
  18. Neuenschwander, A.L.; Magruder, L.A. The Potential Impact of Vertical Sampling Uncertainty on ICESat-2/ATLAS Terrain and Canopy Height Retrievals for Multiple Ecosystems. Remote Sens. 2016, 8, 1039. [Google Scholar] [CrossRef] [Green Version]
  19. Lin, X.; Xu, M.; Cao, C.; Dang, Y.; Bashir, B.; Xie, B.; Huang, Z. Estimates of Forest Canopy Height Using a Combination of ICESat-2/ATLAS Data and Stereo-Photogrammetry. Remote Sens. 2020, 12, 3649. [Google Scholar] [CrossRef]
  20. Hansen, M.C.; Shimabukuro, Y.E.; Potapov, P.; Pittman, K. Comparing annual MODIS and PRODES forest cover change data for advancing monitoring of Brazilian forest cover. Remote Sens. Environ. 2008, 112, 3784–3793. [Google Scholar] [CrossRef]
  21. Abdel-Rahman, E.M.; Ahmed, F.B.; Ismail, R. Random forest regression and spectral band selection for estimating sugarcane leaf nitrogen concentration using EO-1 Hyperion hyperspectral data. Int. J. Remote Sens. 2013, 34, 712–728. [Google Scholar] [CrossRef]
  22. Banskota, A.; Kayastha, N.; Falkowski, M.J.; Wulder, M.A.; Froese, R.E.; White, J.C. Forest Monitoring Using Landsat Time Series Data: A Review. Can. J. Remote Sens. 2014, 40, 362–384. [Google Scholar] [CrossRef]
  23. Puliti, S.; Saarela, S.; Gobakken, T.; Ståhl, G.; Næsset, E. Combining UAV and Sentinel-2 auxiliary data for forest growing stock volume estimation through hierarchical model-based inference. Remote Sens. Environ. 2018, 204, 485–497. [Google Scholar] [CrossRef]
  24. Cho, M.A.; Malahlela, O.; Ramoelo, A. Assessing the utility WorldView-2 imagery for tree species mapping in South African subtropical humid forest and the conservation implications: Dukuduku forest patch as case study. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 349–357. [Google Scholar] [CrossRef]
  25. Vuolo, F.; Żółtak, M.; Pipitone, C.; Zappa, L.; Wenng, H.; Immitzer, M.; Weiss, M.; Baret, F.; Atzberger, C. Data Service Platform for Sentinel-2 Surface Reflectance and Value-Added Products: System Use and Examples. Remote Sens. 2016, 8, 938. [Google Scholar] [CrossRef] [Green Version]
  26. Hu, Y.; Xu, X.; Wu, F.; Sun, Z.; Xia, H.; Meng, Q.; Huang, W.; Zhou, H.; Gao, J.; Li, W.; et al. Estimating Forest Stock Volume in Hunan Province, China, by Integrating In Situ Plot Data, Sentinel-2 Images, and Linear and Machine Learning Regression Models. Remote Sens. 2020, 12, 186. [Google Scholar] [CrossRef] [Green Version]
  27. Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.; Adeli, S.; Brisco, B. Google Earth Engine for geo-big data applications: A meta-analysis and systematic review. ISPRS J. Photogramm. Remote Sens. 2020, 164, 152–170. [Google Scholar] [CrossRef]
  28. Tassi, A.; Vizzari, M. Object-Oriented LULC Classification in Google Earth Engine Combining SNIC, GLCM, and Machine Learning Algorithms. Remote Sens. 2020, 12, 3776. [Google Scholar] [CrossRef]
  29. Seydi, S.; Akhoondzadeh, M.; Amani, M.; Mahdavi, S. Wildfire Damage Assessment over Australia Using Sentinel-2 Imagery and MODIS Land Cover Product within the Google Earth Engine Cloud Platform. Remote Sens. 2021, 13, 220. [Google Scholar] [CrossRef]
  30. Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods – A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
  31. Li, G.; Xie, Z.; Jiang, X.; Lu, D.; Chen, E. Integration of ZiYuan-3 Multispectral and Stereo Data for Modeling Aboveground Biomass of Larch Plantations in North China. Remote Sens. 2019, 11, 2328. [Google Scholar] [CrossRef] [Green Version]
  32. Tokola, T.; Pitkänen, J.; Partinen, S.; Muinonen, E. Point accuracy of a non-parametric method in estimation of forest characteristics with different satellite materials. Int. J. Remote Sens. 1996, 17, 2333–2351. [Google Scholar] [CrossRef]
  33. Chen, Y.; Li, L.; Lu, D.; Li, D. Exploring Bamboo Forest Aboveground Biomass Estimation Using Sentinel-2 Data. Remote Sens. 2018, 11, 7. [Google Scholar] [CrossRef] [Green Version]
  34. García-Gutiérrez, J.; Martínez-Álvarez, F.; Troncoso, A.; Riquelme, J. A comparison of machine learning regression techniques for LiDAR-derived estimation of forest variables. Neurocomputing 2015, 167, 24–31. [Google Scholar] [CrossRef]
  35. Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef] [Green Version]
  36. Zhou, J.-J.; Zhou, Z.; Zhao, Q.; Han, Z.; Wang, P.; Xu, J.; Dian, Y. Evaluation of Different Algorithms for Estimating the Growing Stock Volume of Pinus massoniana Plantations Using Spectral and Spatial Information from a SPOT6 Image. Forests 2020, 11, 540. [Google Scholar] [CrossRef]
  37. Gjertsen, A. Accuracy of forest mapping based on Landsat TM data and a kNN-based method. Remote Sens. Environ. 2007, 110, 420–430. [Google Scholar] [CrossRef]
  38. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  39. Xie, F.; Han, M.; Zhang, W. Singular Homoclinic Bifurcations in a Planar Fast-Slow System. J. Dyn. Control. Syst. 2005, 11, 433–448. [Google Scholar] [CrossRef]
  40. Heumann, B.W. An Object-Based Classification of Mangroves Using a Hybrid Decision Tree—Support Vector Machine Approach. Remote Sens. 2011, 3, 2440–2460. [Google Scholar] [CrossRef] [Green Version]
  41. Wu, C.-H.; Tzeng, G.-H.; Lin, R.-H. A Novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression. Expert Syst. Appl. 2009, 36, 4725–4735. [Google Scholar] [CrossRef]
  42. Tang, L.; Yu, L.; Wang, S.; Li, J.; Wang, S. A novel hybrid ensemble learning paradigm for nuclear energy consumption forecasting. Appl. Energy 2012, 93, 432–443. [Google Scholar] [CrossRef]
  43. Schofield, J.; Daniels, D.; Hammerton, P. A Multiple Migration and Stacking Algorithm Designed for Land Mine Detection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6983–6988. [Google Scholar] [CrossRef] [Green Version]
  44. Li, X.; Liu, Z.; Lin, H.; Wang, G.; Sun, H.; Long, J.; Zhang, M. Estimating the Growing Stem Volume of Chinese Pine and Larch Plantations based on Fused Optical Data Using an Improved Variable Screening Method and Stacking Algorithm. Remote Sens. 2020, 12, 871. [Google Scholar] [CrossRef] [Green Version]
  45. Tsakiridis, N.L.; Tziolas, N.V.; Theocharis, J.B.; Zalidis, G.C. A genetic algorithm-based stacking algorithm for predicting soil organic matter from vis–NIR spectral data. Eur. J. Soil Sci. 2019, 70, 578–590. [Google Scholar] [CrossRef]
  46. Tang, X.; Fehrmann, L.; Guan, F.; Forrester, D.I.; Guisasola, R.; Kleinn, C. Inventory-based estimation of forest biomass in Shitai County, China: A comparison of five methods. Ann. For. Res. 2014, 59, 269–280. [Google Scholar] [CrossRef] [Green Version]
  47. Zhang, Z.; Liu, X.; Ma, Y.; Xu, N.; Zhang, W.; Li, S. Signal Photon Extraction Method for Weak Beam Data of ICESat-2 Using Information Provided by Strong Beam Data in Mountainous Areas. Remote Sens. 2021, 13, 863. [Google Scholar] [CrossRef]
  48. Berninger, A.; Siegert, F. The Potential of ICESat-2 to Identify Carbon-Rich Peatlands in Indonesia. Remote Sens. 2020, 12, 4175. [Google Scholar] [CrossRef]
  49. Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
  50. Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The Ice, Cloud, and Land Elevation Satellite–2 mission: A global geolocated photon product derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef]
  51. Sun, H.; Wang, Q.; Wang, G.; Lin, H.; Luo, P.; Li, J.; Zeng, S.; Xu, X.; Ren, L. Optimizing kNN for Mapping Vegetation Cover of Arid and Semi-Arid Areas Using Landsat images. Remote Sens. 2018, 10, 1248. [Google Scholar] [CrossRef] [Green Version]
  52. Gitelson, A.A.; Viña, A.; Arkebauer, T.J.; Rundquist, D.C.; Keydan, G.; Leavitt, B. Remote estimation of leaf area index and green leaf biomass in maize canopies. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef] [Green Version]
  53. Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
  54. Wallis, C.I.; Homeier, J.; Peña, J.; Brandl, R.; Farwig, N.; Bendix, J. Modeling tropical montane forest biomass, productivity and canopy traits with multispectral remote sensing data. Remote Sens. Environ. 2019, 225, 77–92. [Google Scholar] [CrossRef]
  55. Dimitriadou, E.; Hornik, K.; Leisch, F.; Meyer, D.; Weingessel, A. Misc Functions of the Department of Statistics (e1071); TU Wien: Vienna, Austria, 2008. [Google Scholar]
  56. Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar] [CrossRef] [Green Version]
  57. Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; LeGates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Space Phys. 1985, 90, 8995–9005. [Google Scholar] [CrossRef] [Green Version]
  58. Healey, S.; Yang, Z.; Gorelick, N.; Ilyushchenko, S. Highly Local Model Calibration with a New GEDI LiDAR Asset on Google Earth Engine Reduces Landsat Forest Height Signal Saturation. Remote Sens. 2020, 12, 2840. [Google Scholar] [CrossRef]
  59. Sanchez-Lopez, N.; Boschetti, L.; Hudak, A.; Hancock, S.; Duncanson, L. Estimating Time Since the Last Stand-Replacing Disturbance (TSD) from Spaceborne Simulated GEDI Data: A Feasibility Study. Remote Sens. 2020, 12, 3506. [Google Scholar] [CrossRef]
  60. Adam, M.; Urbazaev, M.; Dubois, C.; Schmullius, C. Accuracy Assessment of GEDI Terrain Elevation and Canopy Height Estimates in European Temperate Forests: Influence of Environmental and Acquisition Parameters. Remote Sens. 2020, 12, 3948. [Google Scholar] [CrossRef]
  61. Rishmawi, K.; Huang, C.; Zhan, X. Monitoring Key Forest Structure Attributes Across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data. Remote Sens. 2021, 13, 442. [Google Scholar] [CrossRef]
  62. Marshak, C.; Simard, M.; Duncanson, L.; Silva, C.; Denbina, M.; Liao, T.-H.; Fatoyinbo, L.; Moussavou, G.; Armston, J. Regional Tropical Aboveground Biomass Mapping with L-Band Repeat-Pass Interferometric Radar, Sparse Lidar, and Multiscale Superpixels. Remote Sens. 2020, 12, 2048. [Google Scholar] [CrossRef]
  63. Boucher, P.B.; Hancock, S.; Orwig, D.A.; Duncanson, L.; Armston, J.; Tang, H.; Krause, K.; Cook, B.; Paynter, I.; Li, Z.; et al. Detecting Change in Forest Structure with Simulated GEDI Lidar Waveforms: A Case Study of the Hemlock Woolly Adelgid (HWA; Adelges tsugae) Infestation. Remote Sens. 2020, 12, 1304. [Google Scholar] [CrossRef] [Green Version]
  64. Silva, C.A.; Duncanson, L.; Hancock, S.; Neuenschwander, A.; Thomas, N.; Hofton, M.; Fatoyinbo, L.; Simard, M.; Marshak, C.Z.; Armston, J.; et al. Fusing simulated GEDI, ICESat-2 and NISAR data for regional aboveground biomass mapping. Remote Sens. Environ. 2021, 253, 112234. [Google Scholar] [CrossRef]
  65. DiMiceli, C.; Townshend, J.; Carroll, M.; Sohlberg, R. Evolution of the representation of global vegetation by vegetation continuous fields. Remote Sens. Environ. 2021, 254, 112271. [Google Scholar] [CrossRef]
Remotesensing 13 01535 g001 550
Figure 1. (a) Locations of the study area; (b) synthetic color image from Sentinel-2 covering Saihanba forest farm, with ICESat-2.
Figure 1. (a) Locations of the study area; (b) synthetic color image from Sentinel-2 covering Saihanba forest farm, with ICESat-2.
Remotesensing 13 01535 g001
Remotesensing 13 01535 g002 550
Figure 2. Histogram of tree species from the FMI in the Saihanba forest farm.
Figure 2. Histogram of tree species from the FMI in the Saihanba forest farm.
Remotesensing 13 01535 g002
Remotesensing 13 01535 g003 550
Figure 3. (a) ATL08 segments covering Saihanba forest farm; (b) the schematic of the ATL08 data; (c) the detailed parameters in the ATL08 segments; (d) larch; (e) Scots pine; (f) spruce.
Figure 3. (a) ATL08 segments covering Saihanba forest farm; (b) the schematic of the ATL08 data; (c) the detailed parameters in the ATL08 segments; (d) larch; (e) Scots pine; (f) spruce.
Remotesensing 13 01535 g003
Remotesensing 13 01535 g004 550
Figure 4. The framework of the stacking algorithm.
Figure 4. The framework of the stacking algorithm.
Remotesensing 13 01535 g004
Remotesensing 13 01535 g005 550
Figure 5. Importance ranking (with standard deviation) of the ASR and height metrics obtained using random forest.
Figure 5. Importance ranking (with standard deviation) of the ASR and height metrics obtained using random forest.
Remotesensing 13 01535 g005
Remotesensing 13 01535 g006 550
Figure 6. Scatter plots of the predicted forest canopy height against the observed values in Saihanba using: (a) MLR; (b) kNN; (c) SVM; (d) RF; (e) stacking.
Figure 6. Scatter plots of the predicted forest canopy height against the observed values in Saihanba using: (a) MLR; (b) kNN; (c) SVM; (d) RF; (e) stacking.
Remotesensing 13 01535 g006
Remotesensing 13 01535 g007 550
Figure 7. (a) Variable importance plot with standard deviations of the random forest analysis resulting from our stacking model; (b) scatterplot of forest canopy height estimates from ICESat-2, and those predicted from Sentinel-2.
Figure 7. (a) Variable importance plot with standard deviations of the random forest analysis resulting from our stacking model; (b) scatterplot of forest canopy height estimates from ICESat-2, and those predicted from Sentinel-2.
Remotesensing 13 01535 g007
Remotesensing 13 01535 g008 550
Figure 8. Spatial distributions of forest canopy height predictions in Saihanba, obtained using stacking, and consisting of (a) predictions from the ICESat-2 footprint area, overlaid on altitude imagery; (b) the spatial distribution of the forest canopy height derived from Sentinel-2.
Figure 8. Spatial distributions of forest canopy height predictions in Saihanba, obtained using stacking, and consisting of (a) predictions from the ICESat-2 footprint area, overlaid on altitude imagery; (b) the spatial distribution of the forest canopy height derived from Sentinel-2.
Remotesensing 13 01535 g008
Remotesensing 13 01535 g009a 550Remotesensing 13 01535 g009b 550
Figure 9. Scatter plots of the predicted forest canopy height by stacking of (a) birch, (b) larch, (c) oak, (d) Scots pine, (e) poplar, and (f) spruce.
Figure 9. Scatter plots of the predicted forest canopy height by stacking of (a) birch, (b) larch, (c) oak, (d) Scots pine, (e) poplar, and (f) spruce.
Remotesensing 13 01535 g009aRemotesensing 13 01535 g009b
Table
Table 1. List of tree species measured in Saihanba.
Table 1. List of tree species measured in Saihanba.
Tree SpeciesNumberValue Range MeanStandard DeviationCoefficient of Variation (%)
Birch12106.1–19.212.472.4920.0
Larch30353.7–20.015.393.6923.9
Poplar736.3–18.614.072.3716.8
Chinese Pine193.7–17.914.473.4824.1
Spruce604.7–18.910.323.4733.6
Oak1454.2–14.36.961.8426.4
Scots Pine8624.9–19.011.162.9926.8
Total54043.7–20.013.763.8828.2
Table
Table 2. Height metrics and apparent surface reflectance extracted from ATL08 used in the study.
Table 2. Height metrics and apparent surface reflectance extracted from ATL08 used in the study.
Independent VariableDescriptionNumber
ASRApparent surface reflectance1
MinimumMinimum height1
MeanMean height1
MedianMedian height1
MaximumMaximum height1
Percentile height25th, 50th, 60th, 70th, 75th, 80th, 85th, 90th, 95th and 98th percentile height10
Table
Table 3. The 98% vegetation canopy height obtained from the ATL08 data in the Saihanba forest farm.
Table 3. The 98% vegetation canopy height obtained from the ATL08 data in the Saihanba forest farm.
Study AreaNumberValue Range MeanStandard DeviationCoefficient of Variation (%)
Saihanba5580–108.161.3816.9
184010–1512.971.3810.6
264015–2017.211.347.8
36520–2521.371.215.6
5404 (Total)4.26–26.4115.113.6223.9
Table
Table 4. List of vegetation indices (VI) used in this study.
Table 4. List of vegetation indices (VI) used in this study.
Vegetation IndexDescriptionReference
Normalized difference vegetation index (NDVI)(NIR − RED)/(NIR + RED)[36]
Red–green vegetation index (RGVI)(RED − GREEN)/(RED + GREEN)[51]
Atmospherically resistant vegetation index (ARVI)NIR − (2 × RED − BLUE)/ NIR+(2 × RED − BLUE)[36]
Enhanced vegetation index (EVI)2.5 × (NIR − RED)/(NIR + 6RED − 7.5 × BLUE + 1)[36]
Visible atmospherically resistant index (VARI)(GRN−RED)/(GRN+RED−BLUE)[51]
Red-edge normalized difference vegetation index a (RENDVI a)(RedEdge1 − RED)/(RedEdge1 + RED)[52]
Red-edge normalized difference vegetation index b (RENDVI b) (RedEdge2 − RedEdge1)/(RedEdge2 + RedEdge1)[53]
Red-edge chlorophyll index (RECI)(RedEdge3/RedEdge1) − 1[54]
Table
Table 5. The correlation coefficient between the ASR, height metrics, and measured forest canopy height.
Table 5. The correlation coefficient between the ASR, height metrics, and measured forest canopy height.
Independent VariableCorrelation CoefficientpIndependent VariableCorrelation Coefficientp
ASR0.060.0070th percentile height0.450.00
Minimum0.050.0075th percentile height0.500.00
Mean0.470.0080th percentile height0.550.00
Median0.320.0085th percentile height0.610.00
Maximum0.660.0090th percentile height0.660.00
25th percentile height0.200.0095th percentile height0.700.00
50th percentile height0.320.0098th percentile height0.710.00
60th percentile height0.380.00---
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the Forest Canopy Height in Northern China by Synergizing ICESat-2 with Sentinel-2 Using a Stacking Algorithm. Remote Sens. 2021, 13, 1535. https://doi.org/10.3390/rs13081535

AMA Style

Jiang F, Zhao F, Ma K, Li D, Sun H. Mapping the Forest Canopy Height in Northern China by Synergizing ICESat-2 with Sentinel-2 Using a Stacking Algorithm. Remote Sensing. 2021; 13(8):1535. https://doi.org/10.3390/rs13081535

Chicago/Turabian Style

Jiang, Fugen, Feng Zhao, Kaisen Ma, Dongsheng Li, and Hua Sun. 2021. "Mapping the Forest Canopy Height in Northern China by Synergizing ICESat-2 with Sentinel-2 Using a Stacking Algorithm" Remote Sensing 13, no. 8: 1535. https://doi.org/10.3390/rs13081535

APA Style

Jiang, F., Zhao, F., Ma, K., Li, D., & Sun, H. (2021). Mapping the Forest Canopy Height in Northern China by Synergizing ICESat-2 with Sentinel-2 Using a Stacking Algorithm. Remote Sensing, 13(8), 1535. https://doi.org/10.3390/rs13081535

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop