Probing the Fault Complexity of the 2017 Ms 7.0 Jiuzhaigou Earthquake Based on the InSAR Data
Abstract
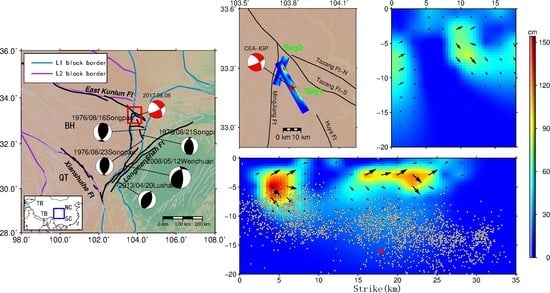
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
3. Model Tests and Results
4. Discussion
4.1. Uncertainty Test
4.2. Fault Geometry and Properties
4.3. Aftershock Distribution
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Q.; Tan, K.; Wang, D.Z.; Zhao, B.; Zhang, R.; Li, Y.; Qi, Y.J. Joint inversion of GNSS and teleseismic data for the rupture process of the 2017 Mw6.5 Jiuzhaigou, China, earthquake. J. Seism. 2018, 22, 805–814. [Google Scholar] [CrossRef]
- Zheng, A.; Yu, X.; Xu, W.; Chen, X.; Zhang, W. A hybrid source mechanism of the 2017 Mw 6.5 Jiuzhaigou earthquake revealed by the joint inversion of strong-motion, teleseismic and InSAR data. Tectonophysics 2020, 789, 228538. [Google Scholar] [CrossRef]
- Ji, L.; Liu, C.; Xu, J.; Liu, L.; Long, F.; Zhang, Z. InSAR observation and inversion of the seismogenic fault for the 2017 Jiuzhaigou MS7.0 earthquake in China. Chin. J. Geophys. 2017, 60, 4069–4082. [Google Scholar]
- Deng, Q.; Cheng, S.; Ma, J.; Du, P. Seismic activities and earthquake potential in the Tibetan Plateau. Chin. J. Geophys. 2014, 57, 2025–2042. [Google Scholar]
- Xu, X.; Chen, G.; Wang, Q.; Chen, L.; Ren, Z.; Xu, C.; Wei, Z.; Lu, R.; Tan, X.; Dong, S.; et al. Discussion on seismogenic structure of Jiuzhaigou earthquake and its implication for current strain state in the southeastern Qinghai-Tibet Plateau. Chin. J. Geophys. 2017, 60, 4018–4026. [Google Scholar]
- Fang, L.; Wu, J.; Su, J.; Wang, M.; Jiang, C.; Fan, L.; Wang, W.; Wang, C.; Tan, X. Relocation of mainshock and aftershock sequence of the Ms7.0 Sichuan Jiuzhaigou earthquake. Chin. Sci. Bull. 2018, 63, 649–662. [Google Scholar] [CrossRef] [Green Version]
- Zebker, H.A.; Rosen, P.A.; Goldstein, R.M.; Gabriel, A.; Werner, C.L. On the derivation of coseismic displacement fields using differential radar interferometry: The Landers earthquake. J. Geophys. Res. Space Phys. 1994, 99, 19617–19634. [Google Scholar] [CrossRef]
- Hussain, E.; Wright, T.J.; Walters, R.J.; Bekaert, D.P.S.; Lloyd, R.; Hooper, A. Constant strain accumulation rate between major earthquakes on the North Anatolian Fault. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef]
- Nie, Z.; Wang, D.-J.; Jia, Z.; Yu, P.; Li, L. Fault model of the 2017 Jiuzhaigou Mw 6.5 earthquake estimated from coseismic deformation observed using Global Positioning System and Interferometric Synthetic Aperture Radar data. Earthplanets Space 2018, 70, 55. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Yue, H.; Shen, Z.; Fang, L.; Zhan, Y.; Sun, X. The 2017 Jiuzhaigou Earthquake: A Complicated Event Occurred in a Young Fault System. Geophys. Res. Lett. 2018, 45, 2230–2240. [Google Scholar] [CrossRef]
- Zhao, D.; Qu, C.; Bürgmann, R.; Gong, W.; Shan, X. Relaxation of Tibetan Lower Crust and Afterslip Driven by the 2001 Mw7.8 Kokoxili, China, Earthquake Constrained by a Decade of Geodetic Measurements. J. Geophys. Res. Solid Earth 2021, 126. [Google Scholar] [CrossRef]
- Malinowska, A.A.; Witkowski, W.T.; Guzy, A.; Hejmanowski, R. Mapping ground movements caused by mining-induced earthquakes applying satellite radar interferometry. Eng. Geol. 2018, 246, 402–411. [Google Scholar] [CrossRef]
- Sopata, P.; Stoch, T.; Wójcik, A.; Mrocheń, D. Land Surface Subsidence Due to Mining-Induced Tremors in the Upper Silesian Coal Basin (Poland)—Case Study. Remote Sens. 2020, 12, 3923. [Google Scholar] [CrossRef]
- Shan, X.; Qu, C.; Gong, W.; Zhao, D.; Zhang, G. Coseismic deformation field of the Jiuzhaigou MS7.0 earthquake from Sentinel-1A InSAR data and fault slip inversion. Chin. J. Geophys. 2017, 60, 4527–4536. [Google Scholar]
- Hong, S.; Zhou, X.; Zhang, K.; Meng, G.; Dong, Y.; Su, X.; Zhang, L.; Li, S.; Ding, K. Source Model and Stress Disturbance of the 2017 Jiuzhaigou Mw 6.5 Earthquake Constrained by InSAR and GPS Measurements. Remote Sens. 2018, 10, 1400. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Qu, C.; Shan, X.; Gong, W.; Zhang, Y.; Zhang, G. InSAR and GPS derived coseismic deformation and fault model of the 2017 Ms7.0 Jiuzhaigou earthquake in the Northeast Bayanhar block. Tectonophyicsics 2018, 726, 86–99. [Google Scholar] [CrossRef]
- Chen, W.; Qiao, X.J.; Liu, G.; Xiong, W.; Jia, Z.G.; Li, Y.; Wang, Y.B.; You, Z.L.; Long, F. Study on the coseismic slip model and Coulomb stress of the 2017 Jiuzhaigou MS7.0 earthquake constrained by GNSS and InSAR measurements. Chin. J. Geophys. 2018, 61, 2122–2132. [Google Scholar]
- Shen, W.; Li, Y.S.; Jiao, Q.; Xie, Q.; Zhang, J. Joint inversion of strong motion and InSAR/GPS data for fault slip distribution of the Jiuzhaigou 7.0 earthquake and its application in seismology. Chin. J. Geophys. 2019, 61, 115–129. [Google Scholar]
- Xie, Z.; Zheng, Y.; Yao, H.; Fang, L.; Liu, C.; Wang, M.; Shan, B.; Zhang, H.; Ren, J.; Ji, L.; et al. Preliminary analysis on the source properties and seismogenic structure of the 2017 Ms7.0 Jiuzhaigou earthquake. Sci. China Earth Sci. 2018, 61, 339–352. [Google Scholar] [CrossRef]
- Gui-Xi, Y.; Feng, L.; Ming-Jian, L.; Hui-Ping, Z.; Min, Z.; You-Qing, Y.; Zhi-Wei, Z.; Yu-Ping, Q.; Si-Wei, W.; Yue, G.; et al. Focal mechanism solutions and seismogenic structure of the 8 August 2017 M7.0 Jiuzhaigou earthquake and its aftershocks, northern Sichuan. Chin. J. Geophys. 2017, 60, 4083–4097. [Google Scholar]
- Hu, X.; Sheng, S.; Wang, Y.; Liang, S. Fault Plane Parameters of 2017 Jiuzhaigou Ms7. 0 Earthquake Determined by Aftershock Distribution. J. Seismol. Res. 2019, 42, 366–371. [Google Scholar]
- Liu, G.; Xiong, W.; Wang, Q.; Qiao, X.; Ding, K.; Li, X.; Yang, S. Source Characteristics of the 2017 Ms 7.0 Jiuzhaigou, China, Earthquake and Implications for Recent Seismicity in Eastern Tibet. J. Geophys. Res. Solid Earth 2019, 124, 4895–4915. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S.B. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. Space Phys. 2005, 110, 1–17. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Coseismic Coulomb stress changes associated with the 2017 MW6.5 Jiuzhaigou earthquake (China) and its impacts on surrounding major faults. Chin. J. Geophys. 2017, 60, 4398–4420. [Google Scholar]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 4, 441–500. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
- Rosen, P.A.; Hensley, S.; Zebker, H.A.; Webb, F.H.; Fielding, E.J. Surface deformation and coherence measurements of Kilauea Volcano, Hawaii, from SIR-C radar interferometry. J. Geophys. Res. Space Phys. 1996, 101, 23109–23125. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. B Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Guo, R.; Zheng, Y.; Diao, F.; Xu, J. Rupture model of the 2013 M W 6.6 Lushan (China) earthquake constrained by a new GPS data set and its effects on potential seismic hazard. Earthq. Sci. 2018, 31, 117–125. [Google Scholar]
- Guo, R.; Zheng, Y.; Xu, J.; Jiang, Z. Seismic and Aseismic Fault Slip Associated with the 2017 M w 8.2 Chiapas, Mexico, Earthquake Sequence. Seismol. Res. Lett. 2019, 90, 1111–1120. [Google Scholar] [CrossRef]
- Wang, R.; Diao, F.; Hoechner, A. SDM—A geodetic inversion code incorporating with layered crust structure and curved fault geometry. In Proceedings of the EGU General Assembly 2013, Vienna, Austria, 7–12 April 2013. [Google Scholar]
- Wang, R.; Martín, F.L.; Roth, F. Computation of deformation induced by earthquakes in a multi-layered elastic crust—FORTRAN programs EDGRN/EDCMP. Comput. Geosci. UK 2003, 29, 195–207. [Google Scholar] [CrossRef]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M.E. CRUST1.0: An updated global model of Earth’s crust. In Proceedings of the EGU General Assembly 2012, Vienna, Austria, 22–27 April 2012. [Google Scholar]
- Wang, Y.; Zhao, T.; Li, C.X.; Liu, C. Relocations and focal mechanism solutions of the 2017 Jiuzhaigou, Sichuan MS 7.0 earthquake sequence. Process Geophys. 2019, 34, 469–478. [Google Scholar]
- Yi, S.-J.; Wu, C.-H.; Li, Y.-S.; Huang, C. Source tectonic dynamics features of Jiuzhaigou Ms 7.0 earthquake in Sichuan Province, China. J. Mt. Sci. 2018, 15, 2266–2275. [Google Scholar] [CrossRef]
- Schnaidt, S.; Heinson, G. Bootstrap resampling as a tool for uncertainty analysis in 2-D magnetotelluric inversion modelling. Geophys. J. Int. 2015, 203, 92–106. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, K.L. Maximum-likelihood event magnitude estimation with bootstrapping for uncertainty estimation. B Seismol. Soc. Am. 1988, 78, 855–862. [Google Scholar]
- Efron, B.; Tibshirani, R. Bootstrap Methods for Standard Errors, Confidence Intervals, and Other Measures of Statistical Accuracy. Stat. Sci. 1986, 1, 54–75. [Google Scholar] [CrossRef]
- Fliss, S.; Bhat, H.S.; Dmowska, R.; Rice, J.R. Fault branching and rupture directivity. J. Geophys. Res. Space Phys. 2005, 110, 110. [Google Scholar] [CrossRef] [Green Version]
- Oglesby, D.D.; Day, S.M.; Li, Y.; Vidale, J.E. The 1999 Hector Mine Earthquake: The Dynamics of a Branched Fault System. B. Seismol. Soc. Am. 2003, 93, 2459–2476. [Google Scholar] [CrossRef]
- Li, Y.; Bürgmann, R.; Zhao, B. Evidence of Fault Immaturity from Shallow Slip Deficit and Lack of Postseismic Deformation of the 2017 Mw 6.5 Jiuzhaigou Earthquake. Bull. Seism. Soc. Am. 2020, 110, 154–165. [Google Scholar] [CrossRef]
- Stein, R.S.; King, G.C.P.; Lin, J. Stress Triggering of the 1994 M = 6.7 Northridge, California, Earthquake by Its Predecessors. Science 1994, 265, 1432–1435. [Google Scholar] [CrossRef]
- Guo, R.; Zheng, Y.; An, C.; Xu, J.; Jiang, Z.; Zhang, L.; Riaz, M.S.; Xie, J.; Dai, K.; Wen, Y. The 2018 Mw 7.9 Offshore Kodiak, Alaska, Earthquake: An Unusual Outer Rise Strike-Slip Earthquake. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019267. [Google Scholar]
- Wang, R.; Lorenzo-Martín, F.; Roth, F. PSGRN/PSCMP—a new code for calculating co- and post-seismic deformation, geoid and gravity changes based on the viscoelastic-gravitational dislocation theory. Comput. Geosci. 2006, 32, 527–541. [Google Scholar] [CrossRef] [Green Version]
- Guo, R.; Zheng, Y.; Xu, J. Stress modulation of the seismic gap between the 2008 M s 8.0 Wenchuan earthquake and the 2013 M s 7.0 Lushan earthquake and implications for seismic hazard. Geophys. J. Int. 2020, 221, 2113–2125. [Google Scholar] [CrossRef]
- Lin, X.; Chu, R.; Zeng, X. Rupture processes and Coulomb stress changes of the 2017 Mw 6.5 Jiuzhaigou and 2013 Mw 6.6 Lushan earthquakes. Earthplanets Space 2019, 71, 1–15. [Google Scholar] [CrossRef]
- Shan, B.; Zheng, Y.; Liu, C.; Xie, Z.; Kong, J. Coseismic Coulomb failure stress changes caused by the 2017 M7.0 Jiuzhaigou earthquake, and its relationship with the 2008 Wenchuan earthquake. Sci. China Earth Sci. 2017, 60, 2181–2189. [Google Scholar] [CrossRef]
- Helmstetter, A.; Shaw, B.E. Relation between stress heterogeneity and aftershock rate in the rate-and-state model. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]









| Nodal Plane I | Nodal Plane II | Magnitude (Mw) | Depth (km) | |
|---|---|---|---|---|
| Strike, Dip, Rake | Strike, Dip, Rake | |||
| GCMT | 242°, 77°, −168° | 150°, 78°, −13° | 6.5 | 14.9 |
| USGS | 246°, 57°, −173° | 153°, 84°, −33° | 6.5 | 13.5 |
| CEA-IGP | 328°, 48°, −11° | 65°, 82°, 137° | 6.5 | 20.0 |
| CEA-IEF | 59°, 77°, 164° | 152°, 75°, 13° | 6.5 | 5.0 |
| Faults | Strike | Dip | Average Error (m) | Maximum Residual (m) | ||
|---|---|---|---|---|---|---|
| One-fault | Main fault | 154° | 51° | 0.0211 | −0.0900 | 6.4 |
| Two-fault | Northern fault | 154° | 66° | 0.0203 | −0.0684 | 6.4 |
| Southern fault | 147° | 74° | ||||
| Three-fault | Northern fault | 156° | 77° | 0.0198 | −0.0602 | 6.4 |
| Southern fault | 147° | 82° | ||||
| Secondary fault | 204° | 80° | ||||
| New two-fault | Main fault | 151° | 77° | 0.0188 | −0.0487 | 6.5 |
| Secondary fault | 196° | 77° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Guo, R.; Xu, J.; Sun, H.; Chen, X.; Zhou, J. Probing the Fault Complexity of the 2017 Ms 7.0 Jiuzhaigou Earthquake Based on the InSAR Data. Remote Sens. 2021, 13, 1573. https://doi.org/10.3390/rs13081573
Tang X, Guo R, Xu J, Sun H, Chen X, Zhou J. Probing the Fault Complexity of the 2017 Ms 7.0 Jiuzhaigou Earthquake Based on the InSAR Data. Remote Sensing. 2021; 13(8):1573. https://doi.org/10.3390/rs13081573
Chicago/Turabian StyleTang, Xiongwei, Rumeng Guo, Jianqiao Xu, Heping Sun, Xiaodong Chen, and Jiangcun Zhou. 2021. "Probing the Fault Complexity of the 2017 Ms 7.0 Jiuzhaigou Earthquake Based on the InSAR Data" Remote Sensing 13, no. 8: 1573. https://doi.org/10.3390/rs13081573
APA StyleTang, X., Guo, R., Xu, J., Sun, H., Chen, X., & Zhou, J. (2021). Probing the Fault Complexity of the 2017 Ms 7.0 Jiuzhaigou Earthquake Based on the InSAR Data. Remote Sensing, 13(8), 1573. https://doi.org/10.3390/rs13081573