Water Budget Closure in the Upper Chao Phraya River Basin, Thailand Using Multisource Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
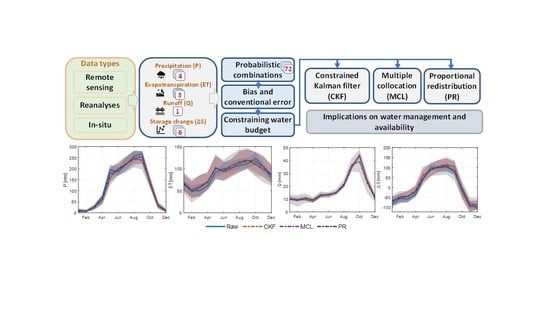
2.2. Water Budget Closure
2.3. Enforcing Water Budget Closure
2.3.1. Constrained Kalman Filter (CKF)
2.3.2. Multiple Collocation (MCL)
2.3.3. Proportional Redistribution (PR)
2.4. Data Used
2.4.1. Precipitation and Evapotranspiration
2.4.2. Terrestrial Water Storage
2.5. Artificial Neural Network
3. Results and Discussion
3.1. Variability among Precipitation and Evapotranspiration Data Products
3.2. Observed Runoff
3.3. Generating Continuous TWSA Time Series
3.4. Raw Ensembles of the Water Budget and Residual Error
3.5. Comparison of Three Water Budget Closure Techniques
3.6. Long-Term Variations and Trends in Corrected Water Budget Components
4. Conclusions
- Various data products, which are based on remote sensing, reanalysis, and in-situ observations, have similar seasonal and annual dynamics, and the variations across products can be attributed to the different retrieval algorithms, model inadequacies, and other biases.
- The ANN model has the potential to fill data gaps between the GRACE and GRACE-FO TWS time series (11 months missing values) and for the sporadically missing values due to battery management practices (a total of 23 missing values during the study period); the latter of which is otherwise filled by using the linear interpolation of the bounding values and thus may underestimate the TWS especially during the peak of the dry or wet season.
- Generally, P tends to have wet bias while ET, Q, and have dry biases. Seasonal time series of the closure constraints of various water budget components reveal a mixed behavior, while the absolute mean annual variability follows the order as > P > ET > Q. Interestingly, a negative (or positive) closure constraint in P does not necessarily imply a positive (or negative) constraint in the remaining components on an annual scale. Knowledge of wet or dry biases of individual components of the water cycle has potential implications for water resources, climate, and agriculture in the basin. For example, correction of an overestimation (underestimation) implicit to P (ET) in the rainy season may avert inaccurate flood (drought) projections.
- The magnitude and sign of closure constraints on various water budget components using the three closure techniques and the resultant partitioning of the water cycle when combined with long term trends in various hydrological and water storage components in our companion study [4] can be effectively used to inform water management especially for mitigation of the adverse effects of drought and floods and for water availability in the basin.
- Although the currently employed water balance closure techniques utilize the unique information from the available scatter of various data products for any given component, the derived combination, though physically consistent, may not be most accurate. This could happen because of similar biases (e.g., dry bias in both P and ET), biases with opposite directions, correlation among various components arising from geophysical variabilities, or simply due to the mathematical artifact [69]. However, the results may serve as the basis for the starting point of getting insights into water availability and other hydrological applications for guiding potential users.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Pan, M.; Sahoo, A.K.; Troy, T.J.; Vinukollu, R.K.; Sheffield, J.; Wood, A.E.F. Multisource estimation of long-term terrestrial water budget for major global river basins. J. Clim. 2012, 25, 3191–3206. [Google Scholar] [CrossRef]
- Abolafia-Rosenzweig, R.; Pan, M.; Zeng, J.L.; Livneh, B. Remotely sensed ensembles of the terrestrial water budget over major global river basins: An assessment of three closure techniques. Remote Sens. Environ. 2021, 252, 112191. [Google Scholar] [CrossRef]
- Abhishek; Kinouchi, T. Synergetic application of GRACE gravity data, global hydrological model, and in-situ observations to quantify water storage dynamics over Peninsular India during 2002–2017. J. Hydrol. 2021, 596, 126069. [Google Scholar] [CrossRef]
- Abhishek; Kinouchi, T.; Sayama, T. A comprehensive assessment of water storage dynamics and hydroclimatic extremes in the Chao Phraya River Basin during 2002–2020. J. Hydrol. 2021, 603, 126868. [Google Scholar] [CrossRef]
- Rodell, M.; Beaudoing, H.K.; L’Ecuyer, T.S.; Olson, W.S.; Famiglietti, J.S.; Houser, P.R.; Adler, R.; Bosilovich, M.G.; Clayson, C.A.; Chambers, D.; et al. The observed state of the water cycle in the early twenty-first century. J. Clim. 2015, 28, 8289–8318. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Karoly, D.; Vicarelli, M.; Neofotis, P.; Wu, Q.; Casassa, G.; Menzel, A.; Root, T.L.; Estrella, N.; Seguin, B.; et al. Attributing physical and biological impacts to anthropogenic climate change. Nature 2008, 453, 353–357. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, M.; Sheffield, J.; Siemann, A.L.; Fisher, C.K.; Liang, M.; Beck, H.E.; Wanders, N.; MacCracken, R.F.; Houser, P.R.; et al. A Climate Data Record (CDR) for the global terrestrial water budget: 1984-2010. Hydrol. Earth Syst. Sci. 2018, 22, 241–263. [Google Scholar] [CrossRef] [Green Version]
- Penatti, N.C.; Almeida, T.I.R.; Ferreira, L.G.; Arantes, A.E.; Coe, M.T. Satellite-based hydrological dynamics of the world’s largest continuous wetland. Remote Sens. Environ. 2015, 170, 31. [Google Scholar] [CrossRef]
- Sheffield, J.; Ferguson, C.R.; Troy, T.J.; Wood, E.F.; McCabe, M.F. Closing the terrestrial water budget from satellite remote sensing. Geophys. Res. Lett. 2009, 36, 07403. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Schmied, H.M.; Van Beek, L.P.H.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C.; et al. Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef] [Green Version]
- Food and Agriculture Organization of the United Nations (FAO). FAO AQUASTAT Country Profile—Thailand; Food and Agriculture Organization of the United Nations: Rome, Italy, 2011. [Google Scholar]
- Turral, H.; Burke, J.; Faurès, J.-M. FAO Water Report 36: Climate Change, Water and Food Security; Food and Agriculture Organization of the United Nations: Rome, Italy, 2008; ISBN 9789251067956. [Google Scholar]
- Supharatid, S. Skill of precipitation projectionin the Chao Phraya river Basinby multi-model ensemble CMIP3-CMIP5. Weather Clim. Extrem. 2015, 12, 14. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, A.K.; Pan, M.; Troy, T.J.; Vinukollu, R.K.; Sheffield, J.; Wood, E.F. Reconciling the global terrestrial water budget using satellite remote sensing. Remote Sens. Environ. 2011, 115, 1850–1865. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Tang, Q.H.; Ferguson, C.R.; Wood, E.F.; Lettenmaier, D.P. Estimating the water budget of major US river basins via remote sensing. Int. J. Remote Sens. 2010, 31, 3955–3978. [Google Scholar] [CrossRef]
- Wang, S.; Huang, J.; Li, J.; Rivera, A.; McKenney, D.W.; Sheffield, J. Assessment of water budget for sixteen large drainage basins in Canada. J. Hydrol. 2014, 512, 15. [Google Scholar] [CrossRef]
- Szeto, K.K.; Tran, H.; MacKay, M.D.; Crawford, R.; Stewart, R.E. The MAGS water and energy budget study. J. Hydrometeorol. 2008, 9, 96–115. [Google Scholar] [CrossRef]
- Panday, P.K.; Coe, M.T.; Macedo, M.N.; Lefebvre, P.; de Almeida Castanho, A.D. Deforestation offsets water balance changes due to climate variability in the Xingu River in eastern Amazonia. J. Hydrol. 2015, 523, 822–829. [Google Scholar] [CrossRef]
- Armanios, D.E.; Fisher, J.B. Measuring water availability with limited ground data: Assessing the feasibility of an entirely remote-sensing-based hydrologic budget of the Rufiji Basin, Tanzania, using TRMM, GRACE, MODIS, SRB, and AIRS. Hydrol. Process. 2014, 28, 853–867. [Google Scholar] [CrossRef]
- Azarderakhsh, M.; Rossow, W.B.; Papa, F.; Norouzi, H.; Khanbilvardi, R. Diagnosing water variations within the Amazon basin using satellite data. J. Geophys. Res. Atmos. 2011, 116, 15997. [Google Scholar] [CrossRef] [Green Version]
- Tang, Q.; Gao, H.; Yeh, P.; Oki, T.; Su, F.; Lettenmaier, D.P. Dynamics of terrestrial water storage change from satellite and surface observations and modeling. J. Hydrometeorol. 2010, 11, 156–170. [Google Scholar] [CrossRef] [Green Version]
- Pan, M.; Fisher, C.K.; Chaney, N.W.; Zhan, W.; Crow, W.T.; Aires, F.; Entekhabi, D.; Wood, E.F. Triple collocation: Beyond three estimates and separation of structural/non-structural errors. Remote Sens. Environ. 2015, 171, 299–310. [Google Scholar] [CrossRef]
- Shiklomanov, A.I.; Yakovleva, T.I.; Lammers, R.B.; Karasev, I.P.; Vörösmarty, C.J.; Linder, E. Cold region river discharge uncertainty-estimates from large Russian rivers. J. Hydrol. 2006, 326, 231–256. [Google Scholar] [CrossRef]
- Pan, M.; Wood, E.F. Data assimilation for estimating the terrestrial water budget using a constrained ensemble Kalman filter. J. Hydrometeorol. 2006, 7, 534–547. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, 25285. [Google Scholar] [CrossRef]
- Long, D.; Chen, X.; Scanlon, B.R.; Wada, Y.; Hong, Y.; Singh, V.P.; Chen, Y.; Wang, C.; Han, Z.; Yang, W. Have GRACE satellites overestimated groundwater depletion in the Northwest India Aquifer? Sci. Rep. 2016, 6, 24398. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
- Longuevergne, L.; Scanlon, B.R.; Wilson, C.R. GRACE hydrological estimates for small basins: Evaluating processing approaches on the High Plains aquifer, USA. Water Resour. Res. 2010, 46, 46. [Google Scholar] [CrossRef]
- Klees, R.; Zapreeva, E.A.; Winsemius, H.C.; Savenije, H.H.G. The bias in GRACE estimates of continental water storage variations. Hydrol. Earth Syst. Sci. 2007, 11, 1227–1241. [Google Scholar] [CrossRef] [Green Version]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, W04531. [Google Scholar] [CrossRef]
- Vishwakarma, B.D.; Horwath, M.; Devaraju, B.; Groh, A.; Sneeuw, N. A Data-Driven Approach for Repairing the Hydrological Catchment Signal Damage Due to Filtering of GRACE Products. Water Resour. Res. 2017, 53, 9824–9844. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Reedy, R.C.; Pool, D.R.; Save, H.; Long, D.; Chen, J.; Wolock, D.M.; Conway, B.D.; Winester, D. Hydrologic implications of GRACE satellite data in the Colorado River Basin. Water Resour. Res. 2015, 51, 9891–9903. [Google Scholar] [CrossRef]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the Global Mass Change Data Record: GRACE Follow-On Instrument and Science Data Performance. Geophys. Res. Lett. 2020, 47, 88306. [Google Scholar] [CrossRef]
- Velicogna, I.; Mohajerani, Y.; Geruo, A.; Landerer, F.; Mouginot, J.; Noel, B.; Rignot, E.; Sutterley, T.; van den Broeke, M.; van Wessem, M.; et al. Continuity of Ice Sheet Mass Loss in Greenland and Antarctica From the GRACE and GRACE Follow-On Missions. Geophys. Res. Lett. 2020, 47, 87291. [Google Scholar] [CrossRef] [Green Version]
- Ciracì, E.; Velicogna, I.; Swenson, S. Continuity of the Mass Loss of the World’s Glaciers and Ice Caps From the GRACE and GRACE Follow-On Missions. Geophys. Res. Lett. 2020, 47, 47. [Google Scholar] [CrossRef]
- Tropical Rainfall Measuring Mission TRMM (TMPA/3B43) Rainfall Estimate L3 1 Month 0.25 Degree × 0.25 Degree V7, Greenbelt, MD, Goddard Earth Sciences Data and Information Services Center (GES DISC). Available online: https://disc.gsfc.nasa.gov/datasets/TRMM_3B42_7/summary (accessed on 15 July 2021).
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Jackson, T. GPM IMERG Final Precipitation L3 Half Hourly 0.1 degree × 0.1 degree V06, Greenbelt, MD, Goddard Earth Sciences Data and Information Services Center (GES DISC). Available online: https://disc.gsfc.nasa.gov/datasets/GPM_3IMERGM_06/summary?keywords=%22IMERG%20final%22 (accessed on 15 July 2021).
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [Green Version]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-present). J. Hydrometeorol. 2003, 4, 7541. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Beaudoing, H.; Rodell, M. NASA/GSFC/HSL GLDAS Noah Land Surface Model L4 monthly 0.25 × 0.25 degree V2.1; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2020. [Google Scholar]
- Martens, B.; Miralles, D.G.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- Reichle, R.H.; Draper, C.S.; Liu, Q.; Girotto, M.; Mahanama, S.P.P.; Koster, R.D.; De Lannoy, G.J.M. Assessment of MERRA-2 land surface hydrology estimates. J. Clim. 2017, 30, 2937–2960. [Google Scholar] [CrossRef] [Green Version]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Save, H. CSR GRACE and GRACE-FO RL06 Mascon Solutions v02. Mascon Solut. 2020, 12, 24. [Google Scholar] [CrossRef]
- Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W.; Watkins, M.M. JPL GRACE Mascon Ocean, Ice, and Hydrology Equivalent Water Height Release 06 Coastal Resolution Improvement (CRI) Filtered Version 1.0.; Physical Oceanography Distributed Active Archive Center: Sacramento, CA, USA, 2020. [Google Scholar]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Dahle, C.; Flechtner, F.; Murböck, M.; Michalak, G.; Neumayer, H.; Abrykosov, O.; Reinhold, A.; König, R. GRACE 327-743 (Gravity Recovery and Climate Experiment), GFZ Level-2 Processing Standards Document for Level-2 Product Release 06 (Rev. 1.0, October 26, 2018), (Scientific Technical Report STR-Data; 18/04); GFZ German Research Centre for Geosci: Potsdam, Germany, 2018. [Google Scholar]
- Dahle, C.; Flechtner, F.; Murböck, M.; Michalak, G.; Neumayer, K.H.; Abrykosov, O.; Reinhold, A.; König, R. GRACE-FO Geopotential GSM Coefficients GFZ RL06. GFZ Data Serv. 2019, 11, 145. [Google Scholar] [CrossRef]
- Meyer, U.; Jaeggi, A.; Dahle, C.; Flechtner, F.; Kvas, A.; Behzadpour, S.; Mayer-Gürr, T.; Lemoine, J.-M.; Bourgogne, S. International Combination Service for Time-variable Gravity Fields (COST-G) Monthly GRACE Series. V. 01. GFZ Data Serv. 2020, 14, 5880. [Google Scholar] [CrossRef]
- Jean, Y.; Meyer, U.; Jäggi, A. Combination of GRACE monthly gravity field solutions from different processing strategies. J. Geod. 2018, 92, 1313–1328. [Google Scholar] [CrossRef] [Green Version]
- Lemoine, J.-M.; Biancale, R.; Reinquin, F.; Bourgogne, S.; Gégout, P. CNES/GRGS RL04 Earth Gravity Field Models, from GRACE and SLR Data. GFZ Data Services. Available online: https://dataservices.gfz-potsdam.de/icgem/showshort.php?id=escidoc:4656890 (accessed on 20 July 2021).
- Loomis, B.D.; Luthcke, S.B.; Sabaka, T.J. Regularization and error characterization of GRACE mascons. J. Geod. 2019, 93, 1381–1398. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Cattani, E.; Merino, A.; Levizzani, V. Evaluation of monthly satellite-derived precipitation products over East Africa. J. Hydrometeorol. 2016, 17, 2555–2573. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Guan, K.; Pan, M.; Li, H.; Wolf, A.; Wu, J.; Medvigy, D.; Caylor, K.K.; Sheffield, J.; Wood, E.F.; Malhi, Y.; et al. Photosynthetic seasonality of global tropical forests constrained by hydroclimate. Nat. Geosci. 2015, 8, 284–289. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef] [Green Version]
- FAO-AQUASTAT Global Information System on Water and Agriculture: Water Resources. Available online: http://www.fao.org/aquastat/en/overview/methodology/water-use%0Ahttp://www.fao.org/aquastat/en/overview/methodology/water-resources/ (accessed on 20 July 2021).
- Pascolini-Campbell, M.; Reager, J.T.; Chandanpurkar, H.A.; Rodell, M. A 10 per cent increase in global land evapotranspiration from 2003 to 2019. Nature 2021, 593, 543–547. [Google Scholar] [CrossRef]
- Richter, H.M.P.; Lück, C.; Klos, A.; Sideris, M.G.; Rangelova, E.; Kusche, J. Reconstructing GRACE-type time-variable gravity from the Swarm satellites. Sci. Rep. 2021, 11, 14. [Google Scholar] [CrossRef]
- Kiguchi, M.; Takata, K.; Hanasaki, N.; Archevarahuprok, B.; Champathong, A.; Ikoma, E.; Jaikaeo, C.; Kaewrueng, S.; Kanae, S.; Kazama, S.; et al. A review of climate-change impact and adaptation studies for the water sector in Thailand. Environ. Res. Lett. 2021, 16, 023004. [Google Scholar] [CrossRef]
- Wong, J.S.; Zhang, X.; Gharari, S.; Shrestha, R.R.; Wheater, H.S.; Famiglietti, J.S. Assessing water balance closure using multiple data assimilation– and remote sensing–based datasets for canada. J. Hydrometeorol. 2021, 22, 131. [Google Scholar] [CrossRef]








| Variable | Dataset | Spatial Resolution and Frequency | References | Remarks |
|---|---|---|---|---|
| Precipitation | TRMM (TMPA) 3B42 V7 | 0.25° × 0.25° Daily | TRMM [39] | Derived by the multi-channel microwave and IR observations from satellites, followed by rescaling based on gauge observations, summing (and applying a factor of three) 3-hourly valid retrievals in a grid cell. |
| GPM IMERG | 0.1° × 0.1° Monthly | Huffman et al. [40] | Intercalibrates and merges the satellite microwave precipitation estimates with microwave-calibrated IR satellite estimates and gauge data using the quasi-Lagrangian time interpolation. | |
| CHIRPS-2.0 | 0.05° × 0.05° Daily | Funk et al. [41] | Incorporates satellite data from NASA and NOAA, and in-situ station data followed by the removal of systematic bias based on IR CCD observations. | |
| GPCP Version 2.3 | 2.5° × 2.5° Monthly | Adler et al. [42] | Integration of various rain gauge stations, satellite data sets and sounding observations. | |
| PERSIANN-CDR | 0.25° × 0.25° Daily | Hsu et al. [43] | Uses the ANN algorithms on GridSat-B1 IR satellite data, ANN training using the NCEP stage IV precipitation data (hourly), and finally bias adjusted using the GPCP monthly product version 2.2. | |
| Evapotranspiration | GLDAS NOAH v2.1 | 0.25° × 0.25° Monthly | Beaudoing et al. [44] | Temporal averaging of 3-hourly GLDAS-2.1 Noah output (Princeton meteorological forcing input data) to produce monthly data followed by the post-processing with the MOD44W MODIS land mask. |
| GLEAM v3.5a | 0.25° × 0.25° Daily | Martens et al. [45] | Uses PT equation with an updated water balance module and updated evaporative stress functions. Extracts maximum information from different components of terrestrial ET (evaporation from bare land and open water, interception, sublimation, transpiration) from the satellite databases. | |
| MERRA-2 | 0.5° × 0.625° Daily | Reichle et al. [46] | Jointly uses the atmospheric general circulation model, atmospheric assimilation system (including modern hyperspectral radiance and microwave observations), an interactive aerosol scheme, and the observed precipitation at the land surface. |
| Variable | Dataset | Spatial Resolution and Frequency | References | Remarks |
|---|---|---|---|---|
| Terrestrial water storage | CSR Mascons RL06M v02 | 0.25° × 0.25° Monthly | Save et al. [47], Save [48] | Corrected for representation on ellipsoidal Earth applied separately to land and ocean to minimize signal leakage. ∆C30 coefficient was replaced with a more accurate estimate from SLR for computing GRACE-FO mascons. |
| JPL Mascons RL06M v02 | 0.5° × 0.5° Monthly | Wiese et al. [49], Watkins et al. [50] | Coastline Resolution Improvement (CRI) filter applied, which leads to reduced leakage errors across coastlines. Realistic geophysical information is introduced during the solution inversion to intrinsically remove correlated error | |
| GFZ Spherical Harmonics RL06 Level-2 | 1° × 1° Monthly | Dahle et al. [51], Dahle et al. [52] | A number of modifications in the static gravity background field, time-variable gravity background field, atmospheric mass variability models, model for planetary ephemerides, parameterization of the accelerometers, processing of GPS constellation have been incorporated compared to the previous versions. | |
| COST G Spherical Harmonics RL02 | 1° × 1° Monthly | Meyer et al. [53], Jean et al. [54] | A harmonization and quality control of the individual input solution level is performed, followed by application of variance component estimation. The resulting COST-G combined gravity fields are validated by assessing their signal and noise content in the spectral and spatial domain. | |
| CNES GRGS Spherical Harmonics RL05 | 1° × 1° Monthly | Lemoine et al. [55] | Latest version of L1B measurements, new model of ocean tides (FES2014b), and IGS orbits and clocks are used instead of GRGS ones are used. The normal matrices are first diagonalized, ordered by decreasing order of the Eigenvalues, and only the best-defined sets of linear combinations of the SH are solved, unlike other SH solutions, which use simple Cholesky inversion. | |
| GSFC Mascons RL06v1.0 | 0.5° × 0.5° Monthly | Loomis et al. [56] | GSFC monthly regularization matrices are determined by analyzing the geographical binning of the inter-satellite range-acceleration pre-fit residuals. The 1-arc-degree equal-area values have been placed on an equal angle 0.5° × 0.5° grid. Land values are determined with a least-squares estimator that conserves mass over each region. |
| TWSA Product | Training (161 Values; May 2002–June 2017) * | Validation (21 Values; June 2018–April 2020) ** | ||||
|---|---|---|---|---|---|---|
| r | NRMSE | NSE | r | NRMSE | NSE | |
| CSR | 0.97 | 0.27 | 0.93 | 0.97 | 0.32 | 0.92 |
| JPL | 0.97 | 0.24 | 0.94 | 0.96 | 0.26 | 0.93 |
| GFZ | 0.94 | 0.32 | 0.89 | 0.91 | 0.37 | 0.82 |
| COST-G | 0.96 | 0.28 | 0.92 | 0.95 | 0.35 | 0.90 |
| CNES GRGS | 0.96 | 0.29 | 0.91 | 0.97 | 0.28 | 0.92 |
| GSFC | 0.95 | 0.30 | 0.90 | 0.96 | 0.28 | 0.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abhishek; Kinouchi, T.; Abolafia-Rosenzweig, R.; Ito, M. Water Budget Closure in the Upper Chao Phraya River Basin, Thailand Using Multisource Data. Remote Sens. 2022, 14, 173. https://doi.org/10.3390/rs14010173
Abhishek, Kinouchi T, Abolafia-Rosenzweig R, Ito M. Water Budget Closure in the Upper Chao Phraya River Basin, Thailand Using Multisource Data. Remote Sensing. 2022; 14(1):173. https://doi.org/10.3390/rs14010173
Chicago/Turabian StyleAbhishek, Tsuyoshi Kinouchi, Ronnie Abolafia-Rosenzweig, and Megumi Ito. 2022. "Water Budget Closure in the Upper Chao Phraya River Basin, Thailand Using Multisource Data" Remote Sensing 14, no. 1: 173. https://doi.org/10.3390/rs14010173
APA StyleAbhishek, Kinouchi, T., Abolafia-Rosenzweig, R., & Ito, M. (2022). Water Budget Closure in the Upper Chao Phraya River Basin, Thailand Using Multisource Data. Remote Sensing, 14(1), 173. https://doi.org/10.3390/rs14010173