Coastal Mean Dynamic Topography Recovery Based on Multivariate Objective Analysis by Combining Data from Synthetic Aperture Radar Altimeter
Abstract
:1. Introduction
2. Method
2.1. Multivariate Objective Analysis
2.2. Error Estimates of Observations
3. Data and Study Area
3.1. Mean Sea Surface Model
3.2. Choice of Global Geopotential Model
3.3. Synthetic/Ocean MDT Models
3.4. Drifting Buoy Data
4. Results
4.1. The Choice of the Estimation of Observation Error on MDT Modeling
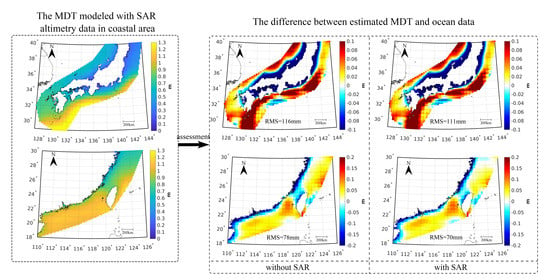
4.2. Assessment of MDTs Modeled with SAR Altimetry Data
5. Discussions
- (1)
- The improvement in the mean sea surface model with SAR altimetry data is limited. The differences between DTU21MSS and DTU18MSS (DTU15MSS) are less than 1 cm in most of the study area. Therefore, the improvement of MDT with SAR altimetry data is limited.
- (2)
- The accuracy and resolution of the reference model that we used for comparison are limited. The accuracy of ocean data ranges from several centimeters to decimeter level. The resolution of ocean data is 15′. The improvement of MDT with SAR altimetry data cannot be well reflected in coastal area.
- (3)
- The geoid model we used is a recently released GRACE/GOCE combined model (DIRR6). The contribution of GOCE is focus on the scale of about 80 km; the shorter scale of signals cannot be reflected in this geoid model. However, the improvement in the mean sea surface model with SAR altimetry data concentrates upon the signals of short scale (tens of kilometers). Moreover, the accuracy and resolution of estimated MDT are mainly restricted by the geoid model. Therefore, the estimated MDT may lack the short scale signals, which leads to the limited improvement of MDT-modeled with SAR altimetry data.
6. Conclusions
- (1)
- The informal approach we used in this study may be suitable for the error estimate of the observations of the multivariate objective analysis method. This approach is particularly useful when the formal errors of the geoid or MDT are difficult to estimate, even over coastal regions, where the errors of input datasets for MDT modeling are hard to model.
- (2)
- The use of the mean sea surface models computed with high-quality SAR altimetry data improves MDT modeling over coastal regions, by a magnitude of about several millimeters. The RMS of the differences between MDT modeled from DTU21MSS (with SAR altimetry data from Sentinel-3A/3B) and ocean data is 8 mm (5 mm) lower than that computed from DTU15MSS (without SAR altimetry data) over the coast of southeastern China (Japan).
- (3)
- Moreover, the use of a SAR-based mean sea surface model improves the computation of local geostrophic velocities, compared with the values computed from the mean sea surface modeled without the SAR altimetry data. The RMS of the differences between the zonal (meridian) velocities derived from MDT modeled with DTU21MSS and the in situ buoy data were 5 mm/s (1 mm/s) less than the results derived from DTU15MSS over the coast of Japan, which is 4 mm/s (2 mm/s) less than the results derived from DTU15MSS over the coast of southeastern China.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lyu, K.; Yang, X.-Y.; Zheng, Q.; Wang, D.; Hu, J. Intraseasonal Variability of the Winter Western Boundary Current in the South China Sea Using Satellite Data and Mooring Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2016, 9, 5079–5088. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Xue, H.; Wang, H. A simple predictive model for the eddy propagation trajectory in the northern South China Sea. Ocean Sci. 2019, 15, 401–412. [Google Scholar] [CrossRef] [Green Version]
- Lin, H.; Thompson, K.R.; Huang, J.; Véronneau, M. Tilt of mean sea level along the Pacific coasts of North America and Japan. J. Geophys. Res. Oceans 2015, 120, 6815–6828. [Google Scholar] [CrossRef] [Green Version]
- Filmer, M.S.; Hughes, C.W.; Woodworth, P.L.; Featherstone, W.E.; Bingham, R.J. Comparison between geodetic and oceanographic approaches to estimate mean dynamic topography for vertical datum unification: Evaluation at Australian tide gauges. J. Geod. 2018, 12, 1413–1437. [Google Scholar] [CrossRef] [Green Version]
- Featherstone, W.E.; Filmer, M.S. The north-south tilt in the Australian Height Datum is explained by the ocean’s mean dynamic topography. J. Geophys. Res. Oceans 2012, 117, C08035. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Abulaitijiang, A.; Featherstone, W.E.; McCubbine, J.C.; Andersen, O.B. Coastal gravity field refinement by combining airborne and ground-based data. J. Geod. 2019, 93, 2569–2584. [Google Scholar] [CrossRef]
- Xu, L.; He, Y.; Huang, W.; Cui, S. A multi-dimensional integrated approach to assess flood risks on a coastal city, induced by sea-level rise and storm tides. Environ. Res. Lett. 2016, 11, 014001. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.J.; Kirwan, M.L. Sea Level-Driven Marsh Migration Results in Rapid Net Loss of Carbon. Geophys. Res. Lett. 2021, 48, e2021GL092420. [Google Scholar] [CrossRef]
- Weisse, R.; Dailidienė, I.; Hünicke, B.; Kahma, K.; Madsen, K.; Omstedt, A.; Parnell, K.; Schöne, T.; Soomere, T.; Zhang, W.; et al. Sea level dynamics and coastal erosion in the Baltic Sea region. Earth Syst. Dyn. 2021, 12, 871–898. [Google Scholar] [CrossRef]
- Genchi, S.A.; Vitale, A.J.; Perillo, G.M.E.; Seitz, C.; Delrieux, C.A. Mapping Topobathymetry in a Shallow Tidal Environment Using Low-Cost Technology. Remote Sens. 2020, 12, 1394. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P. DNSC08 mean sea surface and mean dynamic topography models. J. Geophys. Res. Space Phys. 2009, 114, 1–12. [Google Scholar] [CrossRef]
- Schaeffer, P.; Faugére, Y.; Legeais, J.F.; Ollivier, A.; Guinle, T.; Picot, N. The CNES_CLS11 Global Mean Sea Surface Computed from 16 Years of Satellite Altimeter Data. Mar. Geod. 2012, 35, 3–19. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.; Chambers, D.P.; Bettadpur, S.; Ries, J.C. Large scale ocean circulation from the GRACE GGM01 Geoid. Geophys. Res. Lett. 2003, 30, 2163. [Google Scholar] [CrossRef] [Green Version]
- Pail, R.; Bruinsma, S.; Migliaccio, F.; Förste, C.; Goiginger, H.; Schuh, W.-D.; Höck, E.; Reguzzoni, M.; Brockmann, J.M.; Abrikosov, O.; et al. First GOCE gravity field models derived by three different approaches. J. Geod. 2011, 85, 819–843. [Google Scholar] [CrossRef] [Green Version]
- Pail, R.; Goiginger, H.; Schuh, W.-D.; Hock, E.; Brockmann, J.M.; Fecher, T.; Gruber, T.; Mayer-Gürr, T.; Kusche, J.; Jäggi, A.; et al. Combined satellite gravity field modelGOCO01Sderived from GOCE and GRACE. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Bruinsma, S.L.; Förste, C.; Abrikosov, O.; Marty, J.-C.; Rio, M.-H.; Mulet, S.; Bonvalot, S. The new ESA satellite-only gravity field model via the direct approach. Geophys. Res. Lett. 2013, 40, 3607–3612. [Google Scholar] [CrossRef] [Green Version]
- Bingham, R.J.; Knudsen, P.; Andersen, O.; Pail, R. An initial estimate of the North Atlantic steady-state geostrophic circulation from GOCE. Geophys. Res. Lett. 2011, 38, L01606. [Google Scholar] [CrossRef] [Green Version]
- Volkov, D.L.; Zlotnicki, V. Performance of GOCE and GRACE-derived mean dynamic topographies in resolving Antarctic Circumpolar Current fronts. Ocean Dyn. 2012, 62, 893–905. [Google Scholar] [CrossRef]
- Deng, X.; Featherstone, W.E. A coastal retracking system for satellite radar altimeter waveforms: Application to ERS-2 around Australia. J. Geophys. Res. Oceans 2006, 111, C06012. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O.B.; Scharroo, R. Range and geophysical corrections in coastal regions: And implications for mean sea surface determination. In Coastal Altimetry; Benveniste, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Abulaitijiang, A.; Andersen, O.B.; Stenseng, L. Coastal sea level from inland CryoSat-2 interferometric SAR altimetry. Geophys. Res. Lett. 2015, 42, 1841–1847. [Google Scholar] [CrossRef]
- Dinardo, S.; Fenoglio-Marc, L.; Buchhaupt, C.; Becker, M.; Scharroo, R.; Joana Fernandes, M.; Benveniste, J. Coastal SAR and PLRM altimetry in German bight and west Baltic sea. Adv. Space Res. 2017, 62, 1371–1404. [Google Scholar] [CrossRef]
- Landy, J.C.; Petty, A.A.; Tsamados, M.; Stroeve, J.C. Sea Ice Roughness Overlooked as a Key Source of Uncertainty in CryoSat-2 Ice Freeboard Retrievals. J. Geophys. Res. Oceans 2020, 125, e2019JC015820. [Google Scholar] [CrossRef]
- Gómez-Enri, J.; Vignudelli, S.; Cipollini, P.; Coca, J.; González, C. Validation of CryoSat-2 SIRAL sea level data in the eastern continental shelf of the Gulf of Cadiz (Spain). Adv. Space Res. 2018, 62, 1405–1420. [Google Scholar] [CrossRef] [Green Version]
- Idžanović, M.; Ophaug, V.; Andersen, O.B. Coastal sea level from CryoSat-2 SARIn altimetry in Norway. Adv. Space Res. 2018, 62, 1344–1357. [Google Scholar] [CrossRef] [Green Version]
- Buchhaupt, C.; Fenoglio, L.; Becker, M.; Kusche, J. Impact of vertical water particle motions on focused SAR altimetry. Adv. Space Res. 2021, 68, 853–874. [Google Scholar] [CrossRef]
- Bonnefond, P.; Laurain, O.; Exertier, P.; Boy, F.; Guinle, T.; Picot, N.; Labroue, S.; Raynal, M.; Donlon, C.; Féménias, P.; et al. Calibrating the SAR SSH of Sentinel-3A and CryoSat-2 over the Corsica Facilities. Remote Sens. 2018, 10, 92. [Google Scholar] [CrossRef] [Green Version]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Bretherton, F.P.; Davis, R.E.; Fandry, C.B. A technique for objective analysis and design of oceanographic experiments applied to MODE-73. Deep Sea Res. Oceanogr. Abstr. 1976, 23, 559–582. [Google Scholar] [CrossRef]
- Rio, M.H.; Guinehut, S.; Larnicol, G. New CNES-CLS09 global mean dynamic topography computed from the combination of GRACE data, altimetry, and in situ measurements. J. Geophys. Res. Oceans 2011, 116, C07018. [Google Scholar] [CrossRef]
- Rio, M.H.; Hernandez, F.A. Mean dynamic topography computed over the world ocean from altimetry, in situ measurements, and a geoid model. J. Geophys. Res. Oceans 2004, 109, C12032. [Google Scholar] [CrossRef] [Green Version]
- Rio, M.-H.; Mulet, S.; Picot, N. Beyond GOCE for the ocean circulation estimate: Synergetic use of altimetry, gravimetry, and in situ data provides new insight into geostrophic and Ekman currents. Geophys. Res. Lett. 2014, 41, 8918–8925. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, J.; Shi, H.; He, X. Mean Dynamic Topography Modeling Based on Optimal Interpolation from Satellite Gravimetry and Altimetry Data. Appl. Sci. 2021, 11, 5286. [Google Scholar] [CrossRef]
- Arhan, M.; De Verdiére, A.C. Dynamics of eddy motions in the eastern North Atlantic. J. Phys. Oceanogr. 1985, 15, 153–170. [Google Scholar] [CrossRef] [Green Version]
- Balmino, G. Efficient propagation of error covariance matrices of gravitational models: Application to GRACE and GOCE. J. Geod. 2009, 83, 989–995. [Google Scholar] [CrossRef]
- Bingham, R.J.; Haines, K.; Lea, D.J. How well can we measure the ocean’s mean dynamic topography from space? J. Geophys. Res. Oceans 2014, 119, 3336–3356. [Google Scholar] [CrossRef] [Green Version]
- Oka, E.; Kawabe, M. Dynamic Structure of the Kuroshio South of Kyushu in Relation to the Kuroshio Path Variations. J. Geophys. Res. 2003, 59, 595–608. [Google Scholar] [CrossRef]
- Andersen, O.; Knudsen, P.; Stenseng, L. A New DTU18 MSS Mean Sea Surface–Improvement from SAR Altimetry. In Proceedings of the 25 Years of Progress in Radar Altimetry Symposium, Ponta Delgada, Portugal, 24–29 September 2018. [Google Scholar]
- Zhu, C.; Liu, X.; Guo, J.; Yu, S.; Niu, Y.; Yuan, J.; Gao, Y. Sea Surface Heights and Marine Gravity Determined from SARAL/AltiKa Ka-band Altimeter Over South China Sea. Pure Appl. Geophys. 2021, 178, 1513–1527. [Google Scholar] [CrossRef]
- Jiang, L.; Nielsen, K.; Dinardo, S.; Andersen, O.B.; Bauer-Gottwein, P. Evaluation of Sentinel-3 SRAL SAR altimetry over Chinese rivers. Remote Sens. Environ. 2020, 237, 111546. [Google Scholar] [CrossRef]
- Andersen, O.B.; Abulaitijiang, A.; Zhang, S.; Rose, S.K. A new high resolution Mean Sea Surface (DTU21MSS) for improved sea level monitoring. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. EGU21-16084. [Google Scholar] [CrossRef]
- Förste, C.; Abrykosov, O.; Bruinsma, S.; Dahle, C.; König, R.; Lemoine, J.M. ESA’s Release 6 GOCE Gravity Field Model by Means of the Direct Approach Based on Improved Filtering of the Reprocessed Gradients of the Entire Mission; Data Publication; GFZ Data Services: Potsdam, Germany, 2019. [Google Scholar] [CrossRef]
- Gruber, T. GOCE Release 6 Products and Performance. In Proceedings of the 27th IUGG General Assembly, Montreal, QC, Canada, 8–18 July 2019. [Google Scholar]
- Carton, J.A.; Chepurin, G.A.; Chen, L. SODA3: A New Ocean Climate Reanalysis. J. Clim. 2018, 31, 6967–6983. [Google Scholar] [CrossRef]
- Zuo, H.; Balmaseda, M.A.; Tietsche, S.; Mogensen, K.; Mayer, M. The ECMWF operational ensemble reanalysis–analysis system for ocean and sea ice: A description of the system and assessment. Ocean Sci. 2019, 15, 779–808. [Google Scholar] [CrossRef] [Green Version]
- Mulet, S.; Rio, M.-H.; Etienne, H.; Artana, C.; Cancet, M.; Dibarboure, G.; Feng, H.; Husson, R.; Picot, N.; Provost, C.; et al. The new CNES-CLS18 global mean dynamic topography. Ocean Sci. 2021, 17, 789–808. [Google Scholar] [CrossRef]
- Mayer-Gürr, T.; Kvas, A.; Klinger, B.; Rieser, D.; Zehentner, N.; Pail, R. The combined satellite gravity field model GOCO05s. In Proceedings of the EGU General Assembly, Online, 12–17 April 2015. [Google Scholar]
- Bingham, R.J.; Haines, K. Mean dynamic topography: Intercomparisons and errors. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 903–916. [Google Scholar] [CrossRef] [PubMed]
- Ophaug, V.; Breili, K.; Gerlach, C. A comparative assessment of coastal mean dynamic topography in Norway by geodetic and ocean approaches. J. Geophys. Res. Oceans 2015, 120, 7807–7826. [Google Scholar] [CrossRef] [Green Version]
- Idžanović, M.; Ophaug, V.; Andersen, O.B. The coastal mean dynamic topography in Norway observed by CryoSat-2 and GOCE. Geophys. Res. Lett. 2017, 44, 5609–5617. [Google Scholar] [CrossRef] [Green Version]
- Shi, H.; He, X.; Wu, Y.; Huang, J. The parameterization of mean dynamic topography based on the Lagrange basis functions. Adv. Space Res. 2020, 66. [Google Scholar] [CrossRef]
- Wu, Y.; Abulaitijiang, A.; Andersen, O.B.; He, X.; Luo, Z.; Wang, H. Refinement of Mean Dynamic Topography Over Island Areas Using Airborne Gravimetry and Satellite Altimetry Data in the Northwestern South China Sea. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021805. [Google Scholar] [CrossRef]
- Johnson, G.C. The Pacific Ocean Subtropical cell surface limb. Geophys. Res. Lett. 2001, 28, 1771–1774. [Google Scholar] [CrossRef]
- Lumpkin, R.; Johnson, G.C. Global ocean surface velocities from drifters: Mean, variance, El Niño-Southern Oscillation response, and seasonal cycle. J. Geophys. Res. Oceans 2013, 118, 2992–3006. [Google Scholar] [CrossRef]
- Uchida, H.; Imawaki, S. Eulerian mean surface velocity field derived by combining drifter and satellite altimeter data. Geophys. Res. Lett 2003, 30, 33. [Google Scholar] [CrossRef]
- Hwang, C.; Chen, S.-A. Circulations and eddies over the South China Sea derived from TOPEX/Poseidon altimetry. J. Geophys. Res. Space Phys. 2000, 105, 23943–23965. [Google Scholar] [CrossRef]











| Study Area | Scheme | Min | Max | Mean | RMS |
|---|---|---|---|---|---|
| Coastal area of Japan | Scheme 1 | 111 | 810 | 371 | 397 |
| Scheme 2 | 116 | 830 | 375 | 397 | |
| Scheme 3 | 115 | 791 | 376 | 395 | |
| Southeastern coastal area of China | Scheme 1 | 66 | 1315 | 208 | 274 |
| Scheme 2 | 64 | 1449 | 205 | 273 | |
| Scheme 3 | 67 | 1135 | 220 | 272 |
| Area | Scheme | Min | Max | RMS |
|---|---|---|---|---|
| Coastal area of Japan | Scheme 1 | −465 | 250 | 123 |
| Scheme 2 | −460 | 233 | 120 | |
| Scheme 3 | −445 | 224 | 115 | |
| Southeastern coastal area of China | Scheme 1 | −454 | 154 | 80 |
| Scheme 2 | −478 | 146 | 79 | |
| Scheme 3 | −454 | 149 | 77 |
| Area | MSS Model | Min | Max | RMS |
|---|---|---|---|---|
| Coastal area of Japan | DTU15MSS | −448 | 228 | 116 |
| DTU18MSS | −445 | 224 | 115 | |
| DTU21MSS | −435 | 220 | 111 | |
| Southeastern coastal area of China | DTU15MSS | −450 | 144 | 78 |
| DTU18MSS | −454 | 149 | 77 | |
| DTU21MSS | −437 | 140 | 70 |
| Study Area | MSS Model | Geostrophic Velocities | Min | Max | RMS |
|---|---|---|---|---|---|
| Coastal area of Japan | DTU15MSS | u | −657 | 906 | 179 |
| v | −400 | 711 | 141 | ||
| DTU18MSS | u | −650 | 907 | 178 | |
| v | −401 | 709 | 141 | ||
| DTU21MSS | u | −651 | 901 | 174 | |
| v | −406 | 714 | 140 | ||
| Southeastern coastal area of China | DTU15MSS | u | −267 | 678 | 101 |
| v | −335 | 555 | 107 | ||
| DTU18MSS | u | −260 | 676 | 99 | |
| v | −326 | 553 | 105 | ||
| DTU21MSS | u | −251 | 664 | 97 | |
| v | −325 | 551 | 105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Huang, J.; He, X.; Luo, Z.; Wang, H. Coastal Mean Dynamic Topography Recovery Based on Multivariate Objective Analysis by Combining Data from Synthetic Aperture Radar Altimeter. Remote Sens. 2022, 14, 240. https://doi.org/10.3390/rs14010240
Wu Y, Huang J, He X, Luo Z, Wang H. Coastal Mean Dynamic Topography Recovery Based on Multivariate Objective Analysis by Combining Data from Synthetic Aperture Radar Altimeter. Remote Sensing. 2022; 14(1):240. https://doi.org/10.3390/rs14010240
Chicago/Turabian StyleWu, Yihao, Jia Huang, Xiufeng He, Zhicai Luo, and Haihong Wang. 2022. "Coastal Mean Dynamic Topography Recovery Based on Multivariate Objective Analysis by Combining Data from Synthetic Aperture Radar Altimeter" Remote Sensing 14, no. 1: 240. https://doi.org/10.3390/rs14010240
APA StyleWu, Y., Huang, J., He, X., Luo, Z., & Wang, H. (2022). Coastal Mean Dynamic Topography Recovery Based on Multivariate Objective Analysis by Combining Data from Synthetic Aperture Radar Altimeter. Remote Sensing, 14(1), 240. https://doi.org/10.3390/rs14010240