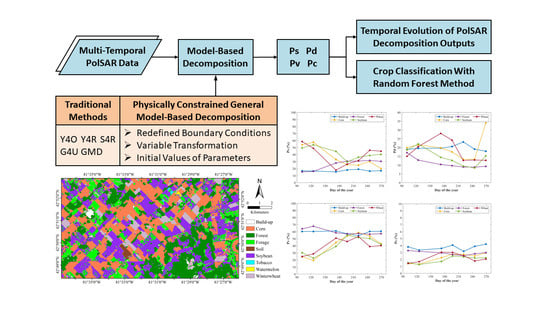
Crop Classification Based on the Physically Constrained General Model-Based Decomposition Using Multi-Temporal RADARSAT-2 Data
Abstract
:1. Introduction
2. Study Area and Dataset
2.1. Study Area and PolSAR Data
2.2. Ground Truth Data
3. Methodology
3.1. General Model-Based Decomposition (GMD)
3.1.1. Surface Scattering Model
3.1.2. Double-Bounce Scattering Model
3.1.3. Volume Scattering Model
3.1.4. Helix Scattering Model
3.1.5. Model Parameters Inversion
3.2. Physically Constrained General Model-Based Decomposition (PCGMD)
3.2.1. Redefined Boundary Conditions
3.2.2. Variable Transformation
3.2.3. Initial Values of Parameters
3.3. Classification Method
4. Results
4.1. PolSAR Decomposition Results
4.2. Crop Classification Results
5. Discussion
5.1. Temporal Evolution of PolSAR Decomposition Outputs
5.2. Crop Classification Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Chen, Z.; Shao, Y.; Chen, J.; Hasi, T.; Pan, H. Research Advances of SAR Remote Sensing for Agriculture Applications: A Review. J. Integr. Agric. 2019, 18, 506–525. [Google Scholar] [CrossRef] [Green Version]
- McNairn, H.; Shang, J.; Jiao, X.; Champagne, C. The Contribution of ALOS PALSAR Multipolarization and Polarimetric Data to Crop Classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3981–3992. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhang, C.; Zhang, S.; Atkinson, P.M. Crop Classification from Full-Year Fully-Polarimetric L-Band UAVSAR Time-Series Using the Random Forest Algorithm. Int. J. Appl. Earth Obs. Geoinf. 2020, 87, 102032. [Google Scholar] [CrossRef]
- Liu, C.; Shang, J.; Vachon, P.W.; McNairn, H. Multiyear Crop Monitoring Using Polarimetric RADARSAT-2 Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2227–2240. [Google Scholar] [CrossRef]
- Steele-Dunne, S.C.; McNairn, H.; Monsivais-Huertero, A.; Judge, J.; Liu, P.W.; Papathanassiou, K. Radar Remote Sensing of Agricultural Canopies: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2249–2273. [Google Scholar] [CrossRef] [Green Version]
- Busquier, M.; Lopez-Sanchez, J.M.; Bargiel, D. Added Value of Coherent Copolar Polarimetry at X-Band for Crop-Type Mapping. IEEE Geosci. Remote Sens. Lett. 2020, 17, 819–823. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J.; Shang, J.; Liao, C.; Liu, J. Application of Polarization Signature to Land Cover Scattering Mechanism Analysis and Classification Using Multi-Temporal C-Band Polarimetric RADARSAT-2 Imagery. Remote Sens. Environ. 2017, 193, 11–28. [Google Scholar] [CrossRef]
- Liao, C.; Wang, J.; Xie, Q.; Al Baz, A.; Huang, X.; Shang, J.; He, Y. Synergistic Use of Multi-Temporal RADARSAT-2 and VENμS Data for Crop Classification Based on 1D Convolutional Neural Network. Remote Sens. 2020, 12, 832. [Google Scholar] [CrossRef] [Green Version]
- Mestre-Quereda, A.; Lopez-Sanchez, J.M.; Vicente-Guijalba, F.; Jacob, A.W.; Engdahl, M.E. Time-Series of Sentinel-1 Interferometric Coherence and Backscatter for Crop-Type Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4070–4084. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, H.; Wang, C.; Zhang, B.; Liu, M. Crop Classification Based on Temporal Information Using Sentinel-1 SAR Time-Series Data. Remote Sens. 2019, 11, 53. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Wang, L.; Kamruzzaman, M.M. Spectral Classification of Ecological Spatial Polarization SAR Image Based on Target Decomposition Algorithm and Machine Learning. Neural Comput. Appl. 2020, 32, 5449–5460. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, J.; Liao, C.; Shang, J.; Lopez-Sanchez, J.M.; Fu, H.; Liu, X. On the Use of Neumann Decomposition for Crop Classification Using Multi-Temporal RADARSAt-2 Polarimetric SAR Data. Remote Sens. 2019, 11, 776. [Google Scholar] [CrossRef] [Green Version]
- Cloude, S.R.; Pottier, E. A Review of Target Decomposition Theorems in Radar Polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Cloude, S.R. Polarisation: Applications in Remote Sensing; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Li, D.; Zhang, Y. Adaptive Model-Based Classification of PolSAR Data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6940–6955. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Y.; Liang, L. A Mathematical Extension to the General Four-Component Scattering Power Decomposition with Unitary Transformation of Coherency Matrix. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7772–7789. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A Three-Component Scattering Model for Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-Component Scattering Model for Polarimetric SAR Image Decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Sato, A.; Boerner, W.M.; Sato, R.; Yamada, H. Four-Component Scattering Power Decomposition With Rotation of Coherency Matrix. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2251–2258. [Google Scholar] [CrossRef]
- Sato, A.; Yamaguchi, Y.; Singh, G.; Park, S.E. Four-Component Scattering Power Decomposition with Extended Volume Scattering Model. IEEE Geosci. Remote Sens. Lett. 2012, 9, 166–170. [Google Scholar] [CrossRef]
- Singh, G.; Yamaguchi, Y.; Park, S.E. General Four-Component Scattering Power Decomposition with Unitary Transformation of Coherency Matrix. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3014–3022. [Google Scholar] [CrossRef]
- Zhang, L.; Zou, B.; Cai, H.; Zhang, Y. Multiple-Component Scattering Model for Polarimetric SAR Image Decomposition. IEEE Geosci. Remote Sens. Lett. 2008, 5, 603–607. [Google Scholar] [CrossRef]
- Singh, G.; Yamaguchi, Y. Model-Based Six-Component Scattering Matrix Power Decomposition. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5687–5704. [Google Scholar] [CrossRef]
- Singh, G.; Malik, R.; Mohanty, S.; Rathore, V.S.; Yamada, K.; Umemura, M.; Yamaguchi, Y. Seven-Component Scattering Power Decomposition of POLSAR Coherency Matrix. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8371–8382. [Google Scholar] [CrossRef]
- Han, W.; Fu, H.; Zhu, J.; Wang, C.; Xie, Q. Polarimetric SAR Decomposition by Incorporating a Rotated Dihedral Scattering Model. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4–8. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Arii, M.; Kim, Y. Model-Based Decomposition of Polarimetric SAR Covariance Matrices Constrained for Nonnegative Eigenvalues. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3452–3459. [Google Scholar] [CrossRef]
- Antropov, O.; Rauste, Y.; Hame, T. Volume Scattering Modeling in PolSAR Decompositions: Study of ALOS PALSAR Data over Boreal Forest. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3838–3848. [Google Scholar] [CrossRef]
- Arii, M.; Van Zyl, J.J.; Kim, Y. A General Characterization for Polarimetric Scattering from Vegetation Canopies. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3349–3357. [Google Scholar] [CrossRef]
- Arii, M.; Van Zyl, J.J.; Kim, Y. Adaptive Model-Based Decomposition of Polarimetric SAR Covariance Matrices. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1104–1113. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Estimation of Forest Structure, Ground, and Canopy Layer Characteristics from Multibaseline Polarimetric Interferometric SAR Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1086–1104. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Wang, X.; Xiao, S.; Sato, M. General Polarimetric Model-Based Decomposition for Coherency Matrix. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1843–1855. [Google Scholar] [CrossRef]
- Xie, Q.; Ballester-Berman, J.D.; Lopez-Sanchez, J.M.; Zhu, J.; Wang, C. Quantitative Analysis of Polarimetric Model-Based Decomposition Methods. Remote Sens. 2016, 8, 977. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Ballester-Berman, J.; Lopez-Sanchez, J.; Zhu, J.; Wang, C. On the Use of Generalized Volume Scattering Models for the Improvement of General Polarimetric Model-Based Decomposition. Remote Sens. 2017, 9, 117. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Zhu, J.; Lopez-Sanchez, J.M.; Wang, C.; Fu, H. A Modified General Polarimetric Model-Based Decomposition Method with the Simplified Neumann Volume Scattering Model. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1229–1233. [Google Scholar] [CrossRef] [Green Version]
- Jiao, X.; Kovacs, J.M.; Shang, J.; McNairn, H.; Walters, D.; Ma, B.; Geng, X. Object-Oriented Crop Mapping and Monitoring Using Multi-Temporal Polarimetric RADARSAT-2 Data. ISPRS J. Photogramm. Remote Sens. 2014, 96, 38–46. [Google Scholar] [CrossRef]
- Li, H.; Zhang, C.; Zhang, S.; Atkinson, P.M. Full Year Crop Monitoring and Separability Assessment with Fully-Polarimetric L-Band UAVSAR: A Case Study in the Sacramento Valley, California. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 45–56. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Lai, K.; Wang, J.; Lopez-Sanchez, J.M.; Shang, J.; Liao, C.; Zhu, J.; Fu, H.; Peng, X. Crop Monitoring and Classification Using Polarimetric Radarsat-2 Time-Series Data across Growing Season: A Case Study in Southwestern Ontario, Canada. Remote Sens. 2021, 13, 1394. [Google Scholar] [CrossRef]
- Lee, J.S.; Schuler, D.L.; Ainsworth, T.L.; Krogager, E.; Kasilingam, D.; Boerner, W.M. On the Estimation of Radar Polarization Orientation Shifts Induced by Terrain Slopes. IEEE Trans. Geosci. Remote Sens. 2002, 40, 30–41. [Google Scholar] [CrossRef]
- An, W.; Cui, Y.; Yang, J. Three-Component Model-Based Decomposition for Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2732–2739. [Google Scholar] [CrossRef]
- An, W.; Xie, C.; Yuan, X.; Cui, Y.; Yang, J. Four-Component Decomposition of Polarimetric SAR Images With Deorientation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1090–1094. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Yajima, Y.; Yamada, H. A Four-Component Decomposition of POLSAR Images Based on the Coherency Matrix. IEEE Geosci. Remote Sens. Lett. 2006, 3, 292–296. [Google Scholar] [CrossRef]
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of Surface Parameters from Polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 727–744. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J.; Shang, J. An Integrated Surface Parameter Inversion Scheme over Agricultural Fields at Early Growing Stages by Means of C-Band Polarimetric RADARSAT-2 Imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2510–2528. [Google Scholar] [CrossRef]
- Di Martino, G.; Iodice, A.; Natale, A.; Riccio, D. Polarimetric Two-Scale Two-Component Model for the Retrieval of Soil Moisture under Moderate Vegetation via L-Band SAR Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2470–2491. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Deschamps, B.; McNairn, H.; Shang, J.; Jiao, X. Towards Operational Radar-Only Crop Type Classification: Comparison of a Traditional Decision Tree with a Random Forest Classifier. Can. J. Remote Sens. 2012, 38, 60–68. [Google Scholar] [CrossRef]
- Liao, C.; Wang, J.; Huang, X.; Shang, J. Contribution of Minimum Noise Fraction Transformation of Multi-Temporal RADARSAT-2 Polarimetric SAR Data to Cropland Classification. Can. J. Remote Sens. 2018, 44, 215–231. [Google Scholar] [CrossRef]
- Sonobe, R.; Tani, H.; Wang, X.; Kobayashi, N.; Shimamura, H. Random Forest Classification of Crop Type Using Multioral TerraSAR-X Dual-Polarimetric Data. Remote Sens. Lett. 2014, 5, 157–164. [Google Scholar] [CrossRef] [Green Version]
- Hariharan, S.; Mandal, D.; Tirodkar, S.; Kumar, V.; Bhattacharya, A.; Lopez-Sanchez, J.M. A Novel Phenology Based Feature Subset Selection Technique Using Random Forest for Multitemporal PolSAR Crop Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4244–4258. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Li, Y.; Wang, X.; Xiao, S.; Sato, M. Modeling and Interpretation of Scattering Mechanisms in Polarimetric Synthetic Aperture Radar: Advances and Perspectives. IEEE Signal Process. Mag. 2014, 31, 79–89. [Google Scholar] [CrossRef]
- Xiang, D.; Tang, T.; Ban, Y.; Su, Y.; Kuang, G. Unsupervised Polarimetric SAR Urban Area Classification Based on Model-Based Decomposition with Cross Scattering. ISPRS J. Photogramm. Remote Sens. 2016, 116, 86–100. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X.; Sato, M. Urban Damage Level Mapping Based on Scattering Mechanism Investigation Using Fully Polarimetric SAR Data for the 3. 11 East Japan Earthquake. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6919–6929. [Google Scholar] [CrossRef]









| Acquisition Date | Mode | Incidence | Resolution | Orbit | Look Direction |
|---|---|---|---|---|---|
| 12 April 2015 | FQ10W | 28.4–31.6° | 5.5 m × 4.7 m | Ascending | Right |
| 6 May 2015 | FQ10W | 28.4–31.6° | 5.5 m × 4.7 m | Ascending | Right |
| 23 June 2015 | FQ10W | 28.4–31.6° | 5.5 m × 4.7 m | Ascending | Right |
| 17 July 2015 | FQ10W | 28.4–31.6° | 5.5 m × 4.7 m | Ascending | Right |
| 10 August 2015 | FQ10W | 28.4–31.6° | 5.5 m × 4.7 m | Ascending | Right |
| 3 September 2015 | FQ10W | 28.4–31.6° | 5.5 m × 4.7 m | Ascending | Right |
| 27 September 2015 | FQ10W | 28.4–31.6° | 5.5 m × 4.7 m | Ascending | Right |
| Land Cover | Training Samples | Testing Samples | ||
|---|---|---|---|---|
| Number of Pixels | Number of Fields | Number of Pixels | Number of Fields | |
| Corn | 6257 | 4 | 20,246 | 16 |
| Soybean | 6505 | 4 | 15,995 | 12 |
| Forage | 3700 | 5 | 3615 | 7 |
| Winter wheat | 6018 | 3 | 17,723 | 16 |
| Watermelon | 310 | 1 | 309 | 1 |
| Tobacco | 416 | 1 | 301 | 1 |
| Forest | 5148 | 4 | 7292 | 6 |
| Built-up | 1267 | 1 | 1117 | 1 |
| Soil | 2331 | 1 | 1592 | 1 |
| Crop Type | Y4O | Y4R | S4R | G4U | GMD | PCGMD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PA | UA | PA | UA | PA | UA | PA | UA | PA | UA | PA | UA | |
| Corn | 95.08 | 85.75 | 95.13 | 85.98 | 95.25 | 85.30 | 95.56 | 86.29 | 94.71 | 84.20 | 96.59 | 88.28 |
| Forest | 99.81 | 97.39 | 99.16 | 98.73 | 99.23 | 98.60 | 99.25 | 98.50 | 99.35 | 96.92 | 99.30 | 98.26 |
| Forage | 84.98 | 61.91 | 86.92 | 61.13 | 85.89 | 62.08 | 86.58 | 61.35 | 85.67 | 65.56 | 88.22 | 67.95 |
| Soil | 93.78 | 100 | 95.04 | 100 | 94.97 | 100 | 95.67 | 100 | 92.21 | 100 | 93.84 | 99.87 |
| Soybean | 95.42 | 92.34 | 94.95 | 93.02 | 94.99 | 93.17 | 94.52 | 93.34 | 94.59 | 89.96 | 93.07 | 94.23 |
| Tobacco | 55.81 | 98.25 | 59.47 | 94.71 | 59.47 | 98.35 | 61.13 | 97.35 | 55.15 | 98.22 | 62.79 | 99.47 |
| Watermelon | 76.05 | 100 | 72.82 | 99.56 | 78.64 | 99.18 | 75.40 | 99.15 | 74.43 | 99.57 | 77.67 | 100 |
| Wheat | 75.14 | 96.78 | 76.26 | 96.88 | 75.71 | 96.69 | 76.54 | 96.49 | 73.16 | 96.65 | 83.48 | 97.76 |
| OA | 89.57 | 89.83 | 89.71 | 89.96 | 88.67 | 91.83 | ||||||
| Kappa | 86.44 | 86.79 | 86.62 | 86.95 | 85.26 | 89.36 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Q.; Dou, Q.; Peng, X.; Wang, J.; Lopez-Sanchez, J.M.; Shang, J.; Fu, H.; Zhu, J. Crop Classification Based on the Physically Constrained General Model-Based Decomposition Using Multi-Temporal RADARSAT-2 Data. Remote Sens. 2022, 14, 2668. https://doi.org/10.3390/rs14112668
Xie Q, Dou Q, Peng X, Wang J, Lopez-Sanchez JM, Shang J, Fu H, Zhu J. Crop Classification Based on the Physically Constrained General Model-Based Decomposition Using Multi-Temporal RADARSAT-2 Data. Remote Sensing. 2022; 14(11):2668. https://doi.org/10.3390/rs14112668
Chicago/Turabian StyleXie, Qinghua, Qi Dou, Xing Peng, Jinfei Wang, Juan M. Lopez-Sanchez, Jiali Shang, Haiqiang Fu, and Jianjun Zhu. 2022. "Crop Classification Based on the Physically Constrained General Model-Based Decomposition Using Multi-Temporal RADARSAT-2 Data" Remote Sensing 14, no. 11: 2668. https://doi.org/10.3390/rs14112668
APA StyleXie, Q., Dou, Q., Peng, X., Wang, J., Lopez-Sanchez, J. M., Shang, J., Fu, H., & Zhu, J. (2022). Crop Classification Based on the Physically Constrained General Model-Based Decomposition Using Multi-Temporal RADARSAT-2 Data. Remote Sensing, 14(11), 2668. https://doi.org/10.3390/rs14112668