An Improved Spatially Variant MOCO Approach Based on an MDA for High-Resolution UAV SAR Imaging with Large Measurement Errors

Abstract

For unmanned aerial vehicle (UAV) synthetic aperture radar (SAR) imaging, motion errors cannot be obtained accurately when high precision motion sensors are not equipped on the platform. This means that traditional data-based motion compensation (MOCO) cannot be directly implemented due to large measurement errors. In addition, classic autofocusing techniques, such as phase gradient autofocus (PGA) or map-drift algorithm (MDA), do not perform well with spatially variant errors, greatly affecting the imaging qualities, especially for high-resolution and large-swath cases. In this study, an improved spatially variant MOCO approach based on an MDA is developed to effectively eliminate the spatially variant errors. Based on the coarse and precise MDA chirp rate error estimation, motion errors are optimally acquired by the random sample consensus (RANSAC) iteration. Two-dimensional (2D) mapping is used to decouple the spatially variant residual errors into two linear independent dimensions so that the chirp-z transform (CZT) can be performed for echo data correction. Unlike traditional approaches, the spatially variant components can be compensated without any measured motion information, which indicates that the proposed approach can be applied to the common UAV SAR system with significant measurement errors. Simulations and real data experiments were used to evaluate the performance of the proposed method. The simulation results show that the proposed algorithm is able to effectively minimize spatially variant errors and generate much better imaging results.

1. Introduction

Airborne synthetic aperture radar (SAR) acquires two-dimensional (2D) high-resolution images using a long coherent integration of the wide bandwidth and pulse width chirp data collected in an aperture [1]. SAR has been widely used in various military and civil applications, such as ground reconnaissance and the detection and recognition of targets [2,3,4,5,6]. Compared with traditional optical and infrared cameras, SAR can be used at any time of the day and in most weather conditions to keep track of the targets and collect more information. In recent years, with the development of unmanned aerial vehicles (UAVs) and integrated circuit boards, mini-SAR systems have been equipped on various drone platforms. One such example is the consumer multi-motor vehicle used in various industrial and agricultural applications, including plant protection, infrastructure inspection, and traffic monitoring, given its easy-to-operate, easy-to-deploy, and low-cost advantages. Instead of its manned counterpart, the UAV SAR can be used for rescue in hazardous conditions, such as earthquakes or fires, to reduce accidental risks.

Ideally, a constant velocity is preferred to ensure that the ground scene can be evenly swept by the antenna beam when the airborne SAR flying; thus, the Doppler bandwidth is synthesized. However, motion can also cause problems in airborne SAR processing. In practice, the platform flight path cannot always be regarded as a straight line due to atmospheric airflows and attitude changes, which can introduce motion errors. In general, motion errors can be classified into two parts, i.e., cross-track and along-track errors [7,8,9].

Cross-track errors are important to identify because they can significantly affect Doppler frequency. The Doppler centroid offset shifts the target position, which generates geometric distortion. The Doppler chirp rate errors destroy the original Doppler pattern of the echo signal, which means that additional phase modulation and envelope migration are both introduced. Since the Doppler chirp rate errors vary with the slant range, they should be compensated at each cell differently instead of making the adjustments simultaneously.

For stable vehicles, such as large transport aircraft, the impact caused by SAR motion errors is not significant; whereas for drones, these errors cannot be ignored because of the frequent turbulence caused by their small size and light weight. Moreover, due to the limited payload of the UAV platform, the radar is usually designed to perform imaging with a high frequency so that the wavelength is very short (e.g., Ka- and Ku-band), resulting in significant phase errors compared to the X-band. In addition, compared to traditional airborne SARs, the detection range of the UAV SAR is so short that the pitch angle of the antenna beam should be large enough to cover the ground scene [10]. Thus, the spatially variant effects of motion errors become significant, which greatly deteriorates the imaging qualities, particularly for high-resolution cases.

Motion compensation (MOCO) for airborne SAR systems is always implemented using recorded data, such as posture (the pitch, the yaw, and the roll angle (PYR)), velocity (the north, the east, and the down (NED)), acceleration (XYZ), and position (the latitude, the longitude, and the radio height). These data are extracted using motion sensors (i.e., inertial navigation system (INS) and global positioning system (GPS)) equipped on the aircraft platform [11,12,13]. During the aperture time, the platform motion errors are acquired based on the instantaneous motion parameters of the navigation coordinate system. Then, the phase compensation and the envelope correction can be performed on the echo signal to implement MOCO. However, due to limitations on payload and cost, the UAVs (particularly consumer UAVs) generally are not equipped with high precision INS or GPS, which means that the measurement errors of motion sensors cannot be ignored and that the most traditional MOCO approaches cannot be directly applied for UAV SAR without improvement.

Several approaches have been developed to implement MOCO using a nonparametric autofocusing algorithm, which means that the de-focused phase errors can be indirectly acquired from the echo data. Autofocusing methods generally fall into two categories: phase-based and magnitude-based approaches. In phased-based systems, the phase differences from sample to sample of the echo data are used to estimate the non-linear phase errors (NPEs). The phase gradient autofocus (PGA) algorithm is a classical method to obtain the NPEs by a series of steps, including scatter selection, windowing, cyclic shifting, and phase gradient estimation [14,15,16]. As a typical phase-based approach, it requires that all targets in the interest area be covered in the same exposure time. PGA algorithm cannot be directly applied in strip-map processing except when de-ramping is used for each sub-aperture since different targets are exposed at different azimuths. Its performance is mainly influenced by prominent scatterers in the illuminated scene, which suggests that PGA applications are greatly limited and may not be applicable for particular locations (e.g., desert, prairie).

Different from the phase-based one, as one of the typical magnitude-based approaches, a map-drift algorithm (MDA) requires contrast features, such as edges and shadows, that are not dependent on strong scatterers [17,18,19,20,21]. The classical MDA has been widely used in lots of airborne SAR processors due to its good performance. In a classical MDA, the full aperture data is divided into a series of sub-apertures with a certain overlap so that the offset of spectrum between sub-looks of each de-focused sub-aperture (segment) can be obtained by cross correlation. Based on the offset, the chirp rate is calculated. In practice, the cross correlation is always summarized from each range cell and considered as the reference one. Thus, the accurate NPEs of full aperture can be integrated from the chirp rate of each segment after being resampled corresponding to the aperture time. By means of NPEs, the MOCO based on the reference can be implemented, which indicates that the variant errors are neglected during processing.

To address this problem, an improved spatially variant MOCO approach is proposed based on an MDA for high-resolution UAV SAR imaging. The received echo data is first divided into several sub-range blocks, and the two-step (coarse and precise) MDA with overlapped sub-apertures (OSA) is performed to estimate the NPEs of all sub-blocks and construct the equations for compensation. To derive the optimal solution, the random sample consensus (RANSAC) algorithm is designed with good robustness and high accuracy. Using the estimated motion errors, two-dimensional (2D) mapping is implemented to decouple the spatially variant residual into two linear independent directions so that the chirp-z transform (CZT) can be performed on the received echo data to remove the spatially variant errors. Compared to the conventional approach, the spatially variant aspects can be compensated without additional measured motion data, which means that the proposed method can be applied to common UAV SAR with significant measurement errors of motion sensors.

The rest of the paper is organized as follows. In Section 2, the geometry model of UAV SAR imaging with motion errors is established, and the effects of spatially variant components and measurement errors are analyzed. In Section 3, an improved spatially variant MOCO approach, consisting of three parts (i.e., a two-step MDA chirp rate estimation, motion errors solution, and spatially variant elimination), is presented in detail. Experimental results, including the simulation and real data processing, are provided in Section 4, and the conclusions are presented in Section 5.

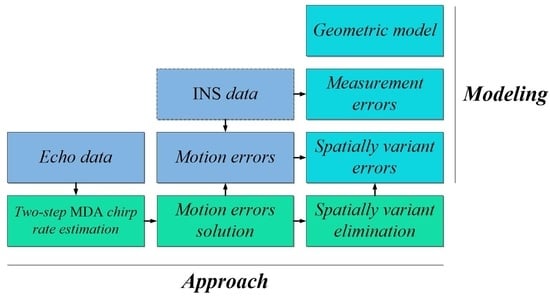
2. Modeling

In this section, the real geometry of the UAV SAR platform, in which the slant range error from the platform to the arbitrary target is expressed with respect to the motion errors is established. The spatially variant and measurement errors that significantly affect the image processing of the UAV SAR are also analyzed.

2.1. Geometric Model

In practice, the aircraft’s motion cannot always be kept constant due to atmospheric turbulence causing offsets from the desired course. The geometric model of the UAV SAR imaging with motion errors is presented in Figure 1. In the Cartesian coordinate system o-xyz, the platform is assumed to fly along the $y$-axis direction. In the figure, the average velocity and altitude are denoted as $v$ and $H$, respectively; $P$ is the center of the footprint; $B$ and $C$ indicate the platform’s instantaneous positions for the real (solid red line) and expected (blue dashed line) paths, the coordinates of which are denoted as $\left[x\left(\eta \right),y\left(\eta \right),z\left(\eta \right)\right]$ and $\left[0,v\eta ,0\right]$, respectively; $A$ is the beam center crossing moment in an aperture, which is always considered as the reference point when processing; and $R_{\mathrm{s}}$ is the reference slant range. The motion error, which is the difference between the real and ideal paths, is denoted as $\left[\mathsf{\Delta }x\left(\eta \right),\mathsf{\Delta }y\left(\eta \right),\mathsf{\Delta }z\left(\eta \right)\right]$. Based on the geometric relationship, the real instantaneous slant range history $r\left(\eta \right)$ of the arbitrary target $Q$ is given by

$$r\left(\eta \right)=\sqrt{{\left[x\left(\eta \right)-x^{\prime }\right]}^2+{\left[y\left(\eta \right)-y^{\prime }\right]}^2+{\left[z\left(\eta \right)-z^{\prime }\right]}^2}$$

(1)

where $\eta$ denotes the azimuth time, and $\left[x^{\prime },y^{\prime },z^{\prime }\right]$ indicates the position of $Q$. Currently, $r\left(\eta \right)$ is simplified by the Taylor series expansion with the high order terms being neglected, i.e.,

$$\begin{array}{ll}r\left(\eta \right)& =\sqrt{{\left[y\left(\eta \right)-y^{\prime }\right]}^2+R_{\mathrm{B}}^2+\mathsf{\Delta }x{\left(\eta \right)}^2+\mathsf{\Delta }z{\left(\eta \right)}^2+2\mathsf{\Delta }x\left(\eta \right)R_{\mathrm{B}}\cos {\theta }_{\mathrm{p}}+2\mathsf{\Delta }z\left(\eta \right)R_{\mathrm{B}}\sin {\theta }_{\mathrm{p}}}\\ & \approx \sqrt{{\left[y\left(\eta \right)-y^{\prime }\right]}^2+R_{\mathrm{B}}^2+2\mathsf{\Delta }x\left(\eta \right)R_{\mathrm{B}}\cos {\theta }_{\mathrm{p}}+2\mathsf{\Delta }z\left(\eta \right)R_{\mathrm{B}}\sin {\theta }_{\mathrm{p}}}\\ & \approx R_{\mathrm{B}}+\frac{{\left[y\left(\eta \right)-y^{\prime }\right]}^2}{2R_{\mathrm{B}}}+\mathsf{\Delta }x\left(\eta \right)\cos {\theta }_{\mathrm{p}}+\mathsf{\Delta }z\left(\eta \right)\sin {\theta }_{\mathrm{p}}\end{array}$$

(2)

where $R_{\mathrm{B}}=R_{\mathrm{s}}$ is assumed as the slant range of the closest approach (for side view, $R_{\mathrm{B}}=R_{\mathrm{s}}$), i.e., $R_{\mathrm{B}}=\sqrt{{x^{\prime }}^2+{z^{\prime }}^2}$; ${\theta }_{\mathrm{p}}$ is defined as the pitch angle, i.e., $x^{\prime }=-R_{\mathrm{B}}\cos {\theta }_{\mathrm{p}}$, $z^{\prime }=R_{\mathrm{B}}\sin {\theta }_{\mathrm{p}}$. The motion errors are extracted from the complex quadratic radical. After expansion, the motion errors are decomposed into two parts: along- and cross-track errors. Numerous advanced techs to address along-track errors have been developed [8,9,10,11], which are always implemented using interpolation or NUFFT. Therefore, it is not further discussed in detail. In addition, cross-track errors are more important to analyze since the spatially variant increases with swath, resolution, aperture length, and pitch angle and cannot be neglected.

A set of experiments are intended to assess phase errors induced by motion errors in different dimensions. Figure 2 shows the simulated ideal motion data (red solid line) and the one measured by low-accuracy INS (blue dashed line) based on the geometric model shown in Figure 1. It can be seen that the platform flies along the $y$-axis, which means that the along-track errors only depend on the motion errors along the $y$-axis. Meanwhile, the cross ones are both determined by the components along the $x$ and the $z$-axes. However, it should be noted that only the ideal motion data (red solid line) is required in the current simulation, and more detail of the measured one will be discussed in Section 2.3. Based on the ideal motion data plotted in Figure 2 and the main parameters of real UAV SAR system summarized in

Table 1. Main parameters of the real UAV SAR system.

Parameters	Value
Bandwidth	750 MHz
Timewidth	100 μs
Carrier frequency	35 GHz
Pulse repeat frequency	625 Hz
Reference range	16,500 m
Velocity	40 m/s
Height	3000 m

, phase errors induced by along-track and cross-track motion errors are plotted in Figure 3a,b, respectively. Compared to the cross one (Figure 3b), the along-track phase errors (Figure 3a) are considerably less than $\pi /4$ so that it can be neglected during our analysis.

The slant range errors $\mathsf{\Delta }r\left(\eta \right)$ of $Q$ can be simplified to:

$$\mathsf{\Delta }r\left(\eta \right)=\mathsf{\Delta }x\left(\eta \right)\sin {\theta }_{\mathrm{p}}+\mathsf{\Delta }z\left(\eta \right)\cos {\theta }_{\mathrm{p}}$$

(3)

As shown by the expression $\mathsf{\Delta }r\left(\eta \right)$, with respect to errors $\mathsf{\Delta }x\left(\eta \right)$ and $\mathsf{\Delta }z\left(\eta \right)$ depend on ${\theta }_{\mathrm{p}}$, which indicates that $\mathsf{\Delta }r\left(\eta \right)$ differs with the range cells and causes variations in range cell migration (RCM) and phase modulation. Designing a proper correction function for $\mathsf{\Delta }r\left(\eta \right)$ in the traditional two-step MOCO is difficult because the independent RCM is always ignored.

2.2. Spatially Variant Errors Analyses

From Equation (3), the variation with respect to the slant range dimension of $\mathsf{\Delta }r\left(\eta \right)$ is mainly determined by ${\theta }_{\mathrm{p}}$, which means the spatially variant error is significant, especially for short-range detection with a large pitch angle [22,23,24]. For analysis, $\cos {\theta }_{\mathrm{p}}$ and $\sin {\theta }_{\mathrm{p}}$ can be expanded with respect to the $\mathsf{\Delta }r$ as

$$\begin{array}{l}\cos {\theta }_{\mathrm{p}}=\frac{H}{R_{\mathrm{B}}}-\frac{H}{R_{\mathrm{B}}^2}\mathsf{\Delta }r+\frac{H}{R_{\mathrm{B}}^3}\mathsf{\Delta }{r}^2+\cdot \cdot \cdot \\ \sin {\theta }_{\mathrm{p}}=1-\frac{H^2}{2R_{\mathrm{B}}^2}-\frac{H^4}{8R_{\mathrm{B}}^4}+\left(\frac{H^2}{R_{\mathrm{B}}^3}-\frac{H^4}{2R_{\mathrm{B}}^5}\right)\mathsf{\Delta }r+\left(\frac{3H^2}{2R_{\mathrm{B}}^4}-\frac{5H^4}{4R_{\mathrm{B}}^6}\right)\mathsf{\Delta }{r}^2+\cdot \cdot \cdot \end{array}$$

(4)

where $\mathsf{\Delta }r$ and $\mathsf{\Delta }{r}^2$ denote the first order and the second order spatially variant components, respectively. The introduced phase errors are simulated based on the system parameters (see Table 1) and motion data (see Figure 2) to analyze the impact of the first- and second-order components, as presented in Figure 4a,b. The high order spatially variant errors are far less than $\frac{\pi }{4}$, which suggests that they can be disregarded in most cases.

2.3. Measurement Errors Analyses

Motion errors have a considerable impact on imaging qualities, which can be removed by conventional two-step MOCO based on motion data which is recorded by the high-accuracy INS mounted on the platform [25]. However, for several UAVs, the accuracy of INS may not meet the motion data-based MOCO requirements [26], which means that the extra NPEs induced by the measurement errors are so significant that they cannot be ignored during imaging processing. In general, measurement errors can be divided into three parts with respect to their effect on focus depth of the dot target.

(1)

Gyroscope north bias: The yaw angle of the platform is measured by a gyroscope, which is an important component of an INS. However, this bias affects the measured heading and further changes the Doppler centroid. Thus, the position is shifted.

(2)

Data rate: In practice, motion data is sampled from INS measurements and saved by recorder. However, it is difficult to synchronize the chirp frame with motion data accurately because the data rate of an INS is much smaller than pulse repetition frequency (PRF) which indicates that the measurement errors are inevitable, and the Doppler chirp rate is changed and thus de-focused.

(3)

Random noise: Random noise exists in all kinds of electronic devices. INS noise introduces the extra high-frequency phase errors during MOCO and raises the grating lobe.

Here, a set of dot target simulations are performed with different MOCO cases. Figure 5a–c show the depth of focus for scenarios without MOCO, with MOCO based on the simulated ideal motion data (the red solid line in Figure 2), and with MOCO based on the simulated motion data measured by low-accuracy INS (the blue dashed line in Figure 2), respectively. Moreover, the gyroscope north bias, the data rate, and the random noise are set as 0.5°, 100 Hz, and 0.02 to simulate the motion data measured a by low-accuracy INS, respectively. It should be noted that the measured data of the x-axis deviates from the ideal one due to the heading error which is caused by gyroscope north bias. Comparing Figure 5c to Figure 5b, the dot targets are defocused and shifted along the azimuthal direction seriously, which suggests that the conventional data-based MOCO cannot support the UAV SAR processing with significant measurement errors and that the signal-based one is more suitable.

3. Approach

From previous analyses, motion parameters recorded by a low-accuracy INS or GPS cannot be directly applied to MOCO because of the impact of additional non-negligible phases and spatially variant errors introduced by significant measured errors. Spatially variant RCMs are always neglected by the traditional two-step MOCO. To address these limitations, an improved MOCO approach is proposed based on an MDA, which can eliminate spatially variant errors. Figure 6 shows the flowchart of the proposed approach. The proposed approach is composed of the following steps:

Step-1: Two-step MDA chirp rate estimation: an MDA is used as the nonparametric autofocusing technique to estimate the NPEs caused by motion errors. The NPEs of the entire aperture are always integrated with respect to the Doppler time from estimated chirp rate errors in all separated sub-segments. Thus, the two-step estimation is adopted. This method is performed after the RCM correction (RCMC), and the NPE compensation is estimated to improve accuracy.

Step-2: Motion errors solution: Spatially variant RCMs caused by motion errors are generally difficult to correct using the classic MDA except when the cross errors are acquired. In our approach, the echo data is separated from the range blocks to get the NPEs by an MDA to construct a set of equations corresponding to the motion errors. The RANSAC algorithm is designed to improve the robustness and accuracy to obtain the optimal solution for the motion errors from these overdetermined equations. Finally, the motion errors estimated by the two-step processing are added.

Step-3: Spatially variant elimination: Using the estimated motion errors, the spatially variant MOCO can be performed. However, the spatially variant errors are cross-coupled, which means that the MOCO cannot be implemented directly unless the received data is decoupled. In our algorithm, after the reference function multiplies (RFM) for the echo data, the 2D mapping corresponding to the slant range, and the Doppler centroid is derived and utilized to decouple the residual spatially variant components of the motion errors into two linear, independent directions. Moreover, CZT processing is applied to remove the spatially variant components.

3.1. Two-Step MDA Chirp Rate Estimation

3.1.1. Sub-Aperture Processing

Unlike the phase-based autofocusing methods, NPEs cannot be acquired directly from the correlation between the segments of the aperture data by magnitude-based autofocusing methods such as an MDA. However, the full aperture data can be separated into several sub-apertures as shown in Figure 7. With the Doppler center removed, NPEs can be double accumulated with azimuth time by the chirp rate which is interpolated and estimated by an MDA of each sub-aperture. In this part, the number of sub-apertures is assumed as $N$ with duration $T_{\mathrm{s}}$. Particularly, the restricting condition should be satisfied, i.e.,

$$\varphi \left({\eta }_i+\epsilon \right)={\gamma }_i{\epsilon }^2$$

(5)

where ${\eta }_i$ is the center moment of the i-th sub-aperture, $\epsilon \in \left(-\frac{T_{\mathrm{s}}}{2},\frac{T_{\mathrm{s}}}{2}\right)$ denotes the azimuth time during the sub-aperture, and ${\gamma }_i$ is assumed as the real Doppler chirp rate error of the i-th sub-aperture, which is greatly affected by motion errors. Note that the estimation accuracy ${\gamma }_i$ is determined by the NPEs, which are derived from the map-drift. The full aperture is split into half-overlap segments to ensure the continuation of the NPEs $\varphi \left({\eta }_i+\epsilon \right)$ between sub-apertures, which is important in determining the accuracy of the phase combination. The chirp rate error $\widehat{\gamma }\left(\eta \right)$ is derived by the interpolations of the estimated results $\left[\begin{array}{cccc}{\widehat{\gamma }}_1& {\widehat{\gamma }}_2& \dots & {\widehat{\gamma }}_N\end{array}\right]$, i.e.,

$$\widehat{\gamma }\left(\eta \right)={\displaystyle \sum _{j=1}^L{\widehat{\gamma }}_i\left(j\right)\sin \mathrm{c}\left(\eta -j\right)}$$

(6)

where ${\widehat{\gamma }}_i$ is the estimated result by the i-th sub-aperture data $L$ is the length of the interpolation core. Linear interpolation is utilized to reduce the computational load instead of sinc. The NPEs of the full aperture can be derived by:

$$\begin{array}{l}\widehat{f_{\mathrm{D}}}\left(\eta \right)={\displaystyle {\int }_{-\frac{T_{\mathrm{s}}}{2}}^{\frac{T_{\mathrm{s}}}{2}}\widehat{\gamma }\left(\eta \right)d\eta }\\ \widehat{\varphi }\left(\eta \right)={\displaystyle {\int }_{-\frac{T_{\mathrm{s}}}{2}}^{\frac{T_{\mathrm{s}}}{2}}\left[\widehat{f_{\mathrm{D}}}\left(\eta \right)-\overline{\widehat{f_{\mathrm{D}}}\left(\eta \right)}\right]d\eta }\end{array}$$

(7)

where $\widehat{f_{\mathrm{D}}}\left(\eta \right)$ and $\widehat{\varphi }\left(\eta \right)$ denote the Doppler frequency errors and the NPEs, respectively. $\overline{\widehat{f_{\mathrm{D}}}\left(\eta \right)}$ is the average of $\widehat{f_{\mathrm{D}}}\left(\eta \right)$, representing the linear part and generating the azimuth shift of image and should therefore be removed.

3.1.2. Map-Drift Chirp Rate Estimation

The accuracy of NPEs is always determined by the estimated sub-apertures chirp rate error ${\widehat{\gamma }}_i$. The weight-MDA is developed to improve the accuracy of chirp rate estimation. The weight $w_i\left(\tau \right)$ is defined as

$$w_i\left(\tau \right)=\sqrt{\frac{{\displaystyle \sum _{\epsilon }{\left|S_i\left(\tau ,\epsilon \right)-\frac{{\displaystyle \sum _{\epsilon }{S}_i\left(\tau ,\epsilon \right)}}{n_{\mathrm{s}}}\right|}^2}}{n_{\mathrm{s}}}}$$

(8)

where $n_{\mathrm{s}}$ denotes the length of the sub-aperture, and $\tau$ denotes the fast time. By using the contrast of each range cell as a weight, it is beneficial to select range cells with strong features and improve the robustness and accuracy of chirp rate estimation.

After the de-chirp processing, the echo signal of the i-th sub-aperture can be decomposed as:

$$S_i\left(\tau ,\epsilon \right)=\overline{S_i}\left(\tau ,\epsilon \right)\cdot \exp \left[j\pi {\gamma }_i\left(\tau \right){\epsilon }^2\right]$$

(9)

where $\overline{S_i}\left(\tau ,\epsilon \right)$ denotes the echo signal corresponding to the reference target, and the exponent term denotes the QPE of motion errors. To obtain ${\widehat{\gamma }}_i\left(\tau \right)$, $S_i\left(\tau ,\epsilon \right)$ should be separated into two sub-blocks without overlap, i.e.,

$$\begin{array}{l}{S}_{i,1}\left(\tau ,\epsilon \right)=S_i\left(\tau ,\epsilon -\frac{T_{\mathrm{s}}}{2}\right)=\overline{S_i}\left(\tau ,\epsilon -\frac{T_{\mathrm{s}}}{2}\right)\cdot \exp \left[j\pi {\gamma }_i\left(\tau \right){\left(\epsilon -\frac{T_{\mathrm{s}}}{2}\right)}^2\right]\\ S_{i,2}\left(\tau ,\epsilon \right)=S_i\left(\tau ,\epsilon +\frac{T_{\mathrm{s}}}{2}\right)=\overline{S_i}\left(\tau ,\epsilon +\frac{T_{\mathrm{s}}}{2}\right)\cdot \exp \left[j\pi {\gamma }_i\left(\tau \right){\left(\epsilon +\frac{T_{\mathrm{s}}}{2}\right)}^2\right]\end{array}$$

(10)

The azimuthal spectrums of (10) can be expressed as

$$\begin{array}{l}{S}_{i,1}\left(\tau ,f_{\epsilon }\right)=S_i\left[\tau ,f_{\epsilon }+\frac{{\gamma }_i\left(\tau \right)T_{\mathrm{s}}}{2}\right]\\ S_{i,2}\left(\tau ,f_{\epsilon }\right)=S_i\left[\tau ,f_{\epsilon }-\frac{{\gamma }_i\left(\tau \right)T_{\mathrm{s}}}{2}\right]\end{array}$$

(11)

where $f_{\epsilon }$ denotes the azimuth frequency. Moreover, ${\gamma }_i\left(\tau \right)$ can be described by the frequency shift between $S_{i,1}\left(\tau ,f_{\epsilon }\right)$ and $S_{i,2}\left(\tau ,f_{\epsilon }\right)$ as

$${\widehat{\gamma }}_i\left(\tau \right)=\frac{4\mathsf{\Delta }\widehat{f_{\epsilon }}\left(\tau \right)}{T_{\mathrm{s}}^2}$$

(12)

where $\mathsf{\Delta }\widehat{f}\left(\tau \right)$ is the frequency shift. However, the estimation accuracy for the range cells cannot always be guaranteed, which indicates that an optimization method should be adopted. In this part, the weight $w_i\left(\tau \right)$ can be applied to reduce the effect of bad cell estimation, which is given by

$${\widehat{\gamma }}_i=\frac{{\displaystyle \sum _{\tau }{w}_i\left(\tau \right)\cdot {\widehat{\gamma }}_i\left(\tau \right)}}{n}$$

(13)

where $n$ denotes the range cell number.

3.1.3. Coarse and Precise Processing

The accurate phase errors are difficult to obtain from signal-based estimation, especially for UAVs affected by significant atmospheric turbulence. The extra RCMs introduced by motion errors deteriorate the accuracy and cannot be ignored. Generally, this problem can be effectively addressed by the two-step processing.

First, the first MDA, defined as the coarse value, is used to acquire the main part of the NPEs $\widehat{\varphi }\left(\eta \right)$ of the raw echo data. Utilizing $\widehat{\varphi }\left(\eta \right)$, both the phase multiplication and envelope correction can be performed on the data so that the second MDA, which is the precise value, can be performed after RCMC processing to accurately estimate the residual NPEs. These functions are expressed as follows:

$$\begin{array}{l}{H}_1\left(f_{\tau },\eta \right)=\exp \left[-j\widehat{\varphi }\left(\eta \right)f_{\tau }{f}_0\right]\\ H_2\left(\tau ,\eta \right)=\exp \left[-j\widehat{\varphi }\left(\eta \right)\right]\end{array}$$

(14)

where $f_{\tau }$ and $f_0$ denote the range and carrier frequencies, respectively.

3.2. Motion Errors Solution

3.2.1. NPEs Equations Construction

The NPEs, estimated by the two-step MDA, cannot be directly applied for the UAV SAR MOCO because of the additional spatially variant motion errors $\mathsf{\Delta }x\left(\eta \right)$ and $\mathsf{\Delta }z\left(\eta \right)$, which cannot be ignored (see Section 2.1). The spatially variant NPEs are reconstructed by performing the two-step MDA on sub-blocks in the range direction, given by the expression [27,28]:

$$\left[\begin{array}{ll}\cos {\theta }_{\mathrm{p}}^{\left(1\right)}\hfill & \sin {\theta }_{\mathrm{p}}^{\left(1\right)}\hfill \\ \cos {\theta }_{\mathrm{p}}^{\left(2\right)}\hfill & \sin {\theta }_{\mathrm{p}}^{\left(2\right)}\hfill \\ \dots \hfill & \dots \hfill \\ \cos {\theta }_{\mathrm{p}}^{\left(N\right)}\hfill & \sin {\theta }_{\mathrm{p}}^{\left(N\right)}\hfill \end{array}\right]\cdot \left[\begin{array}{c}\mathsf{\Delta }x\left(\eta \right)\\ \mathsf{\Delta }z\left(\eta \right)\end{array}\right]=\left[\begin{array}{c}\frac{\lambda }{4\pi }{\varphi }_1\left(\eta \right)\\ \frac{\lambda }{4\pi }{\varphi }_2\left(\eta \right)\\ \dots \\ \frac{\lambda }{4\pi }{\varphi }_N\left(\eta \right)\end{array}\right]$$

(15)

where the superscript $N$ denotes the sub-block number; $R_{\mathrm{s}}^{\left(i\right)}$ and $\mathsf{\Delta }{\varphi }_i\left(\eta \right)$ are the reference slant range and the NPEs of i-th block, respectively; ${\theta }_{\mathrm{p}}^{\left(i\right)}$ is the pitch angle from the platform to the center of i-th block, i.e., ${\theta }_{\mathrm{p}}^{\left(i\right)}=\arcsin \left[H/R_{\mathrm{s}}^{\left(i\right)}\right]$; and $R_{\mathrm{s}}^{\left(i\right)}$ and $\lambda$ are the reference slant range of i-th block and wave length, respectively. Theoretically, to acquire the $\mathsf{\Delta }x\left(\eta \right)$ and $\mathsf{\Delta }z\left(\eta \right)$ from (15), only two equations are required, which can be constructed from any two blocks. However, in practice, the estimated NPEs cannot be guaranteed to be accurate. Thus, the echo data should be divided as much as possible to construct the overdetermined equations to solve the best solution. For convenience, these linear equations can be expressed in matrix form:

$$\left[\begin{array}{ll}\cos {\theta }_{\mathrm{p}}^{\left(1\right)}\hfill & \sin {\theta }_{\mathrm{p}}^{\left(1\right)}\hfill \\ \cos {\theta }_{\mathrm{p}}^{\left(2\right)}\hfill & \sin {\theta }_{\mathrm{p}}^{\left(2\right)}\hfill \\ \dots \hfill & \dots \hfill \\ \cos {\theta }_{\mathrm{p}}^{\left(N\right)}\hfill & \sin {\theta }_{\mathrm{p}}^{\left(N\right)}\hfill \end{array}\right]\cdot \left[\begin{array}{c}\mathsf{\Delta }x\left(\eta \right)\\ \mathsf{\Delta }z\left(\eta \right)\end{array}\right]=\left[\begin{array}{c}\frac{\lambda }{4\pi }{\varphi }_1\left(\eta \right)\\ \frac{\lambda }{4\pi }{\varphi }_2\left(\eta \right)\\ \dots \\ \frac{\lambda }{4\pi }{\varphi }_N\left(\eta \right)\end{array}\right]\Rightarrow \mathit{A}\cdot \mathit{x}=\mathit{b}$$

(16)

3.2.2. RANSAC Solution

Generally, $\mathit{x}$ is derived as

$$\mathit{x}={\mathit{A}}^{+}\mathit{b}$$

(17)

where ${\mathit{A}}^{+}$ denotes the Moore–Penrose pseudoinverse of $\mathit{A}$ when it is a square or not a singular matrix. Note that $\mathit{x}$ is greatly affected by the accuracy of the NPEs estimation or the sub-block data quality, which indicates that the precision cannot be ensured for the UAV SAR. To increase the robustness of the solution, the RANSAC algorithm is designed and adopted to obtain the optimal result $\mathit{x}$ of (17), and the detailed procedures are as follows:

Step 1: First, establish a binary quadratic equation by selecting the two equations from the NPEs set in (16) to judge the validity of the corresponding data. The binary quadratic equation is given by

$${\mathit{A}}^{\prime }{\mathit{x}}^{\prime }={\mathit{b}}^{\prime }$$

(18)

Step2: Solve the ${\mathit{x}}^{\prime }$ in (18) if the determinant of ${\mathit{A}}^{\prime }$ is not zero; otherwise, resume Step 1, which can be expressed as

$${\mathit{x}}^{\prime }={\mathit{A}}^{-1}\mathit{b}\left|\mathit{A}\right|\ne 0$$

(19)

where ${\mathit{A}}^{-1}$ denotes the inverse matrix of ${\mathit{A}}^{\prime }$.

Step3: Substitute ${\mathit{x}}^{\prime }$, which is regarded as the maybe-solution into (16), to obtain the $\widehat{\mathit{b}}$ for each block.

Step4: Compute the Euclidean distance $\mathsf{\sigma }$ between $\widehat{\mathit{b}}$ and $\mathit{b}$ of each block, which can be derived by:

$$\mathsf{\sigma }={\Vert \mathit{b}-\widehat{\mathit{b}}\Vert }_2$$

(20)

Count the number $n_{\mathrm{In}}$ of blocks whose Euclidean distance is less than the threshold ${\sigma }_T$ (regarded as inliers). If the number of inliers exceeds $N_{\mathrm{In}}$, which denotes the minimum threshold for the number of inliers, $x^{\prime }$ can be adopted as a well-solution and is stored with respect to $n_{\mathrm{In}}$ in a group $X=\left\{\left(x_{\left(i\right)}^{\prime },n_{\mathrm{In}\left(i\right)}\right)|i\in \left[1,N_{\mathrm{Iter}}\right]\right\}$, where $N_{\mathrm{Iter}}$ is the number of iterations. Then, restart the iteration from Step 1 to Step 4 until $N_{\mathrm{Iter}}$ is reached.

Step5: Select the satisfactory $x^{\prime }$ from the group $X$ as the best solution for $x$ if the corresponding $n_{\mathrm{In}}$ is the largest.

With the incorporation of the RANSAC processing into the two-step MDA chirp rate estimation, the spatially variant motion errors can be eliminated.

3.3. Spatially Variant Estimation

3.3.1. Decoupling Processing Based on 2D Mapping

After performing RFM for the arbitrary target $Q$, the spatially variant residual phase errors in the raw data can be expressed when the arbitrary complex magnitudes are ignored [29,30]:

$$\begin{array}{ll}{S}^{\prime }\left(f_{\tau },\eta \right)& =S\left(f_{\tau },\eta \right)\cdot H_{\mathrm{RFM}}\left(f_{\tau },\eta \right)\\ & =\exp \left[-j\frac{4\pi \left(f_{\tau }+f_0\right)}{c}r\left(\eta \right)\right]\cdot \exp \left[j\frac{4\pi \left(f_{\tau }+f_0\right)}{c}{r}_{\mathrm{s}}\left(\eta \right)\right]\\ & =\exp \left[-j\frac{4\pi \left(f_{\tau }+f_0\right)}{c}\mathsf{\Delta }r\left(\eta \right)\right]\end{array}$$

(21)

where $f_0$ denotes the carrier frequency. The variant slant range history $\mathsf{\Delta }r\left(\eta \right)$ of $Q$ corresponding to the reference point can be expressed as the difference between $r\left(\eta \right)$ with $r_{\mathrm{s}}\left(\eta \right)$. The motion errors obtained by the two-step processing cannot be applied directly to eliminate the variant errors because the range and azimuthal dimensions of the phase component in (21) are cross-coupling in the 2D time domain [31,32]. However, the 2D signal spectrum after azimuthal FFT processing is derived as

$$\begin{array}{ll}{S}^{\prime }\left(f_{\tau },f_{\eta }\right)& =\exp \left[j{\theta }^{\prime }\left(f_{\tau },f_{\eta }\right)\right]\\ & =\exp \left[-j\frac{4\pi \mathsf{\Delta }r}{c}\sqrt{{\left(f_0+f_{\tau }\right)}^2-\frac{c^2{f}_{\eta }^2}{4v^2}}\right]\end{array}$$

(22)

where $\mathsf{\Delta }r$ denotes the differential range corresponding to the reference point at the position of zero Doppler. For convenience, the phase function ${\theta }^{\prime }\left(f_{\tau },f_{\eta }\right)$ of (23) can be expanded to:

$${\theta }^{\prime }\left(f_{\tau },f_{\eta }\right)\Rightarrow -\frac{4\pi \mathsf{\Delta }r}{c}\left[f_0\sqrt{1-\frac{c^2{f}_{\eta }^2}{4f_0^2{v}^2}}+\frac{1}{\sqrt{1-\frac{c^2{f}_{\eta }^2}{4f_0^2{v}^2}}}{f}_{\tau }-\frac{\frac{c^2{f}_{\eta }^2}{4f_0^2{v}^2}}{2f_0{\left(\sqrt{1-\frac{c^2{f}_{\eta }^2}{4f_0^2{v}^2}}\right)}^3}{f}_{\tau }^2\right]$$

(23)

The first term is the residual azimuth modulation; the second term is the differential RCM, and the third term is the residual range-azimuth cross-coupling. To remove these terms, 2D mapping can be constructed to decompose ${\theta }^{\prime }\left(f_{\tau },f_{\eta }\right)$ into two individual parts, $g_1\left(f_{\tau },f_{\eta }\right)$ and $g_2\left(f_{\tau },f_{\eta }\right)$, using the equation:

$$\{\begin{array}{l}{g}_1\left(f_{\tau },f_{\eta }\right)=f_0\sqrt{1-\frac{c^2{f}_{\eta }^2}{4f_0^2{v}^2}}+\frac{1}{\sqrt{1-\frac{c^2{f}_{\eta }^2}{4f_0^2{v}^2}}}{f}_{\tau }\\ g_2\left(f_{\tau },f_{\eta }\right)=-\frac{\frac{c^2{f}_{\eta }^2}{4f_0^2{v}^2}}{2f_0{\left(\sqrt{1-\frac{c^2{f}_{\eta }^2}{4f_0^2{v}^2}}\right)}^3}{f}_{\tau }^2\end{array}$$

(24)

where $g_1\left(f_{\tau },f_{\eta }\right)$ and $g_2\left(f_{\tau },f_{\eta }\right)$ are functions with respect to $f_{\tau }$ and $f_{\eta }$. Thus, (23) can be defined as the function corresponding to $g_1$ and $g_2$, given by:

$$\begin{array}{ll}{S}^{\prime }\left(f_{\tau },f_{\eta }\right)& =S^{\prime }\left[g_1\left(f_{\tau },f_{\eta }\right),g_2\left(f_{\tau },f_{\eta }\right)\right]\\ & =\exp \left[-j\frac{4\pi \mathsf{\Delta }r}{c}{g}_1\left(f_{\tau },f_{\eta }\right)\right]\exp \left[-j\frac{4\pi \mathsf{\Delta }r}{c}{g}_2\left(f_{\tau },f_{\eta }\right)\right]\end{array}$$

(25)

The cross-coupling 2D signal spectrum is separated into two independent exponents in the mapping domain constructed by $g_1$ and $g_2$, which means that phase errors are decoupled, and the spatially variant processing can be performed. In addition, the new range and the Doppler position of the target after mapping can be regarded as the projection from $\mathsf{\Delta }r$ to $g_1$ and $g_2$, respectively.

3.3.2. CZT Correction

The nonlinear functions $g_1$ and $g_2$ correspond to $f_{\tau }$ and $f_{\eta }$. The spatially variant errors are difficult to remove using the multiply coefficient, so the echo data should be resampled in the mapping domain. CZT is recommended instead of the complicated interpolation $g_1$ to reduce the computational load [33,34,35,36]. The block diagram is shown in Figure 8. $H_1$ and $H_2$ are as follows:

$$H_1\left(f_{\tau },\eta \right)=\exp \left[-j\pi \frac{1}{m}\left(1+\frac{f_{\tau }}{f_0}\right){\left(\frac{g_1}{\mathsf{\Delta }{g}_1}\right)}^2\right]$$

(26)

$$H_2\left(\tau ,\eta \right)=\exp \left[-j\frac{4\pi f_0{v}^2{\eta }^2}{c^2\tau }\right]$$

(27)

where $m$ is the azimuthal size, and $\mathsf{\Delta }{g}_1$ is the resampled interval $g_1$.

4. Experiment

To evaluate the performance of the proposed method, simulation and real data experiments were conducted.

4.1. Simulation Results

In the simulation, the ground scene size was set to 400 m $\times$ 400 m, with 32 point targets randomly placed, and the parameters in Table 1 and the instantaneous velocities in Figure 2 were then analyzed. For comparative experiments, the INS instantaneous output with a large measurement error was also simulated.

Figure 9a–c show the imaging results processed using an INS, a classic MDA, and the proposed approach, respectively. The results show that the performance of the INS-based MOCO was unsatisfactory, with most targets being out of focus due to significant measurement errors. This indicates that an INS-based MOCO cannot be directly applied to UAV SAR. The difference in performance between the classic MDA and the proposed approach is shown in the 2D profile of selected targets in Figure 10b,c and Figure 11b,c, and PSLRs are listed in

Table 2. PSLRs of selected targets.

	Dot-1	Dot-2
MOCO by the INS	−1.90	−2.17
MOCO by the MDA	−10.36	−12.82
MOCO by the Proposed approach	−12.25	−12.84

. In addition, the estimated, measured and ideal motion errors for simulated experiment are plotted in Figure 12. The root mean-square (RMS) corresponding to the ideal motion errors can further demonstrate the accuracy of our approach. Due to the spatially variant residual errors, the focusing quality of the target was unsatisfactory, especially at the edges of the ground scene, and the resolution was worse compared to the proposed approach.

4.2. Real Data Experiment Results

Raw data with significant motion errors were collected by a high-resolution fixed–wing UAV SAR with the size of 6 m × 3.8 m × 1.4 m (span × length × height); the system parameters are shown in Table 1. INS accuracies of velocity and posture were 0.2 m/s and 0.5°, respectively. Additionally, the data rate was 125 Hz. Figure 13a–c show the imaging results processed by an INS, the classic MDA, and the proposed approach, respectively.

In addition, two different regions were selected from the SAR image for comparative analysis and are shown in Figure 14 and Figure 15. The results show that the proposed algorithm was able to focus strong scatterer much better, which further demonstrates the superiority of our algorithm. The estimated and measured motion errors were then plotted and are presented in Figure 16. The resulting graphs suggest that the measured data is significantly less precise compared to the estimated values, which further deteriorates the imaging quality.

5. Conclusions

In this paper, an improved spatially variant MOCO approach is proposed based on an MDA for high-resolution UAV SAR imaging with large measurement errors. Motion errors were acquired accurately using a two-step MDA chirp rate error estimation and the RANSAC solution for NPE equations. Using the estimated motion errors, 2D mapping was developed to decouple the spatially variant residual errors into two linearly independent directions so that the CZT could correct the signal data. Compared with the conventional approach, the spatially variant components of motion errors can be eliminated without any measured motion data. The results suggest that the proposed method can be applied to the UAV SAR with significant measurement errors.