Next Article in Journal
PoSDMS: A Mining System for Oceanic Dynamics with Time Series of Raster-Formatted Datasets
Next Article in Special Issue
Wavefield Decomposition of Ocean-Bottom Multicomponent Seismic Data with Composite Calibration Filters
Previous Article in Journal
Optimal Sensor Placement Using Learning Models—A Mediterranean Case Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 13
10.3390/rs14132990
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Crustal Electrical Structure of the Ganzi Fault on the Eastern Tibetan Plateau: Implications for the Role of Fluids in Earthquakes

by
Yuanzhi Cheng
1,
Yanlong Kong
1,*,
Zhongxing Wang
2,
Yonghui Huang
3 and
Xiangyun Hu
4
1
Key Laboratory of Shale Gas and Geoengineering, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
2
CAS Engineering Laboratory for Deep Resources Equipment and Technology, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
3
College of Geosciences, China University of Petroleum, Beijing 102249, China
4
Institute of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(13), 2990; https://doi.org/10.3390/rs14132990
Submission received: 24 April 2022 / Revised: 31 May 2022 / Accepted: 20 June 2022 / Published: 22 June 2022
(This article belongs to the Special Issue Geophysical Data Processing in Remote Sensing Imagery)
Browse Figures
Review Reports Versions Notes

Abstract

:
The initiation and evolution of seismic activity in intraplate regions are controlled by heterogeneous stress and highly fractured rocks within the rock mass triggered by fluid migration. In this study, we imaged the electrical structure of the crust beneath the Ganzi fault using a three-dimensional magnetotelluric inversion technique, which is host to an assemblage of resistive and conductive features extending into the lower crust. It presents a near-vertical low-resistance zone that cuts through the brittle ductile transition zone, extends to the lower crust, and acts as a pathway for fluid migration from the crustal flow to the upper crustal depths. Conductors in the upper and lower crust are associated with saline fluids and 7% to 16% partial melting, respectively. The relationship between the earthquake epicenter and the surrounding electrical structure suggests that the intraplate seismicity is triggered by overpressure fluids, which are dependent on fluid volume changes generated by the decompression dehydration of partially molten material during upwelling and native fluid within the crustal flow.

Graphical Abstract

1. Introduction

Since the Cenozoic period, the uplift of the Tibetan Plateau and the major shortening of the underlying crust have been caused by the continental collision between the Indian and Eurasian plates and the ongoing intracontinental convergence [1,2,3,4]. The movement of the Indian plate has been largely absorbed by the intracontinental deformations that occurred on the Tibetan Plateau and its surrounding areas, resulting in large-scale earthquakes and tectonic activity [5,6,7]. Intracontinental deformation occurs primarily along large-scale strike-slip faults, such as the Ganzi-Xianshuihe fault in the eastern part of the Tibetan Plateau [8,9,10]. The Global Positioning System (GPS) results show that the tectonic deformation in the eastern margin of the Tibetan Plateau is dominated by clockwise rotation around the eastern Himalayan syntax [11,12,13]. The tectonic deformation model of the Tibetan Plateau has been a recent topic of debate in this field of research. Based on plane indentation experiments, Tapponnier et al. proposed that the material inside the Tibetan Plateau escaped eastward along the large strike-slip faults under the compression of the Indian plate during the collision, and the tectonic deformation inside the block was weak or negligible [14]. As a result of the context of the topography of the Tibetan Plateau and its surrounding areas, a dynamic model of the lower crustal flow was proposed. This suggests the presence of viscous fluid flows up to 15-km thick within the underlying crust of the eastern edge of the Tibetan Plateau, flowing out of the plateau. After being blocked by the strong South China Block, the crustal material from the weak central plateau accumulates in the middle and lower crust, resulting in a sudden thickening of the crust and a strong uplift of the surface [15,16].
The Ganzi fault (Figure 1), located on the eastern edge of the Tibetan Plateau, is a left-lateral strike-slip fault with a history of heavy activity in the late Quaternary period. Hot springs are present across the fault. Earthquakes have been recorded in each section of the fault, including the M6.5 Yushu earthquake in the northwest segment, the M7 Dengke earthquake in 1896 in the middle segment, the M7.7 earthquake in 1854 and the M7.3 earthquake in 1866 in the southeast section, and the M8 Zhuqing earthquake in 1320 ± 65 [10,17,18,19,20]. The earthquake history and paleo-earthquake relics of the fault show repeated characteristics of large earthquakes within short time periods [17,18]. The Ganzi and Xianshuihe faults together form the southwestern boundary of the Bayan Har Block [2]. Since the start of the 20th century, more than 10 earthquakes with a magnitude greater than 7 have occurred along the edge of this block, with two earthquakes of a magnitude greater than 8 in the past 10 years (2008 Wenchuan MS8 earthquake and 2001 East Kunlun MS8.1 earthquake) [21,22]. These earthquakes are closely linked to the eastward expansion of the Tibetan Plateau and the related accumulation and release of stress at the block boundary. These complex tectonic features and frequent earthquake activities provide crucial information about the crustal movement and tectonic deformation of the eastern margin of the Tibetan Plateau [17]. Its tectonic deformation features and deep structure provide useful evidence for deciphering the deformation mode and earthquake mechanism of the Tibetan Plateau. Particularly after the Wenchuan and Yushu earthquakes, useful research results have been obtained. However, existing research primarily focuses on seismic geology, seismic deformation monitoring, strike-slip rate, and fault initiation chronology [10,17,19,20,23]. As a result, the deep structure beneath the Ganzi fault lacks fine geophysical data constraints. In this study, the magnetotelluric (MT) method was used to obtain an understanding of the deep fine structure of the Ganzi fault, to determine the relevant geometric and kinematic features, and to discuss the mechanism of strong earthquakes.
The MT method, when used with a natural electromagnetic field with rich spectral components as the field source, can detect the electrical structure of the lithosphere. Natural field signals can penetrate high-resistance areas of the geology with ease and are very sensitive to low-resistance bodies [24]. The MT method can effectively visualize the deep fluid distribution and the deep structure of the fault. This has an important constraining effect on the deep contact relationship between large geological blocks and the regional seismogenic background [25,26,27,28,29,30,31]. As computing power has increased, it now allows inversions to be completed in days (or hours) instead of weeks. Therefore, 3D inversion of magnetotelluric data is now almost a standard process [32,33,34,35]. In regions with complex geological structures, even with careful consideration of the electromagnetic survey layout, the data in some places will inevitably be 3D. With the development of 3D inversion codes and the increasing availability of high-performance computing equipment, MT data are now typically collected in arrays rather than transects, necessitating inversion using 3D inversion codes. In addition, where transects are collected, it is now becoming more common to use 3D inversion codes to perform inversions to achieve 3D representations of the data [34,36,37]. In recent years, MT soundings carried out on the eastern edge of the Tibetan Plateau have found widely distributed low-resistance layers in the middle and lower crust [38,39,40], which are considered to be the electrical reflection of the material flow [37,41,42,43,44,45,46]. The MT results in these seismically active areas not only reveal the previously hidden seismogenic structure, but also show that the occurrence of moderate to strong earthquakes is closely related to the subsurface electrical structure of the active faults. In addition, they show that the crustal electrical structure may control the occurrence of earthquakes [30,31,40,41,42]. Therefore, there is a close relationship between the crustal flows’ migration in the eastern margin of the Tibetan Plateau and the activities of moderate and strong earthquakes. The Ganzi fault zone, located at a critical location for the eastward migration of crustal flows, is an ideal site for deciphering the relationship between fluids and seismicity. In this study, MT data of the Ganzi fault zone were first collected to obtain the crustal electrical structure through 3D inversion. Secondly, we estimated the fluid distribution and discussed the relationship between fluid and seismic activity (Figure 2).

2. Geological Setting

The Ganzi fault is a highly active left-lateral strike-slip fault in the Holocene deposit with a total length of nearly 500 km along the NW strike. Together with the Xianshuihe fault, this constitutes the boundary between the Bayan Har Block and the Sichuan-Yunnan Block [10,17,20]. This fault dips to the northeast, with an angle of 70–85° near the surface and a fractured zone with a width of 50 to several hundred meters, primarily distributed in the Triassic strata [20]. The traces of this fault are primarily distributed in alluvial-diluvial, glacial diluvial, and residual slope wash in the late Quaternary deposit, in a left en-echelon step-over arrangement [10]. The landforms are characterized by the linear extension of fault scarps, slope-troughs, and left-lateral displacements. In the remote-sensing images, the faults display clear linear features, alongside phenomena including river and river offsets and slop-middle troughs, with predominantly left-lateral strike-slip accompanied by small vertical movements [20]. The average slip rate of the Ganzi fault in the late Quaternary deposit is 7 mm/year [10]. The average slip rate since 50 ka is 12 mm/year [17], and the current slip rate observed by GPS is approximately 10 mm/year. The initiation age of the left-lateral strike-slip motion is estimated to be 6–8 Ma, with approximately the same activity rate as the Xianshuihe fault [12].
The Ganzi fault can be divided into three segments according to the activity and spatial distribution features in different regions: the Ganzi segment (southeast), the Dengke-Cuoa segment (middle), and the Dengke-Yushu segment (northwest) [19]. The Ganzi segment, which is 54 km long, extends from the Ganzi pull-apart Basin to the Cuoa Basin along the in a northwestern direction. The activity in this fault is dominated by sinistral strike-slip with a component of thrust [20]. Due to its close proximity, the area between the Ganzi and Xianshuihe faults is affected by the overall left strike-slip movement of the Ganzi fault. This area has been in an extensional tectonic environment for a long time, which has generated a series of secondary strike-slip faults with a left step-over [9]. Following long-term geological evolution, these secondary faults eventually formed the present-day Ganzi pull-apart Basin [17]. The exposed strata in the southeastern segment of the Ganzi fault are primarily Triassic and Quaternary in nature, among which the Triassic strata are the most widely distributed, with Jurassic acid granites distributed on the southwestern side of the fault (Figure 3). The maximum left-lateral stream offsets of the Jinsha and Yalong Rivers are 80 km and 35 km along the Ganzi fault, respectively (Figure 1) [9,10]. Along the various segments of the fault, there is evidence of surface ruptures caused by historical earthquakes. The length of the surface rupture in the northwestern segment is over 70 km, corresponding to the M7.3 earthquake in 1896. The length of the surface rupture in the middle segment is approximately 180 km, formed by the M7.7 earthquake in 1854. The length of the surface rupture in the southeastern segment is approximately 65 km, with maximum coseismic left-lateral offsets of 5.3 m, produced by the M7.3 earthquake in 1866 [17].

3. Magnetotelluric Data and Analysis

The broadband MT data was collected at 19 sites along two intersecting survey transects across the Ganzi fault during August 2021 (Figure 3). The average distance between the MT sites outside the Ganzi fault was 5 km, and the sites at the Ganzi fault had a spacing of 1 km. The time series of two electric field components and three magnetic field components were recorded for over 20 h with a Phoenix MTU-5 system and Surface Electromagnetic Prospecting system [47] at the MT sites. The magnetic field components were detected by induction coil magnetic sensors, and the telluric field components were detected by nonpolarized Pb-PbCl2 electrodes with an electrical dipole length of 50 m. The time series data of all MT sites were transformed into frequency-domain impedance tensors using SSMT2000 software with remote reference and statistically robust algorithms [48,49]. Due to the relatively low electromagnetic noise in the study area, the maximum period of the impedance tensor of the majority of MT sites was over 1000 s, which is suitable for probing the crustal structure, even when taking into account the presence of conductors in the crust. Most MT sites displayed smooth response curves, and Figure 4 shows representative apparent resistivity and phase curves from nine selected MT sites.
The phase tensor, derived from a second-rank tensor of the impedance tensor, provides an efficient method for evaluating the dimensionality of the subsurface electrical feature. One advantage of this approach is that the results are free from the influence of galvanic distortion because of the presence of inhomogeneities in near-surface structures [50]. Figure 5 shows a pseudo-section of normalized phase tensor ellipses with the values of the skew angle (β) and the geometric mean phase (Φ1). The skew angle of the MT sites within the Quaternary pull-apart Basin (A01–A05 and B03–B09) shows low values (≤5°) at short periods (<1 s), indicating the presence of one-dimensional shallow young sediments. At longer periods (>1 s), high skew values (≥5°) were observed at MT sites in the vicinity of the Ganzi fault, reflecting the presence of three-dimensional (3D) geoelectric structures at a greater depth. The geometric mean (Φ1) of the maximum (Φmax) and minimum (Φmin) phases represent the variation in resistivity with depth [51]. Phase values of MT sites at the southern end of the profile (B1 and B2) were less than 45° at short periods (<0.1 s), which correspond to the presence of surface granite with high resistivity. The Φ1 values began to rise for longer period values (>1 s), indicating that the resistivity decreased as the depth increased. This reveals the existence of low-resistivity anomalies in this region. In contrast, a broad region of high value appears in the deep structure of the Ganzi fault at the maximum period of 1000 s, indicating the presence of high conductivity features in the middle-lower crust.

4. Inversion and Results

According to the phase tensor analysis (Figure 5), there is a 3D electrical structure in the middle-lower crust beneath the Ganzi fault. This is indicated by the large skew angle, β, for the longer periods. It is essential to obtain a good understanding of the electrical structure of the study region, and this can be achieved by using the 3D inversion method. The data from 19 MT sites were used in a 3D MT inversion package (ModEM) alongside a nonlinear conjugate gradient algorithm and parallel computing [52,53]. All elements of the impedance tensor (Zxx, Zxy, Zyy, and Zyx) were employed in the 3D inversion process. Twenty periods were used ranging from 320 Hz to 1300 s. The error floor for the antidiagonal impedance components was set to 5% of Zxy and Zyx, and the error floor of Zxx and Zyy was set to 10% of the diagonal impedance components. The model grids consisted of 78 cells in the north-south direction, 32 cells in the east-west direction, and 53 cells in the vertical direction, with the horizontal spacing of 1 km in the N–S direction and 3 km in the E–W direction. In the vertical direction, the thickness of the grid was set to 20 m at the surface, and then successively increased by a factor of 1.2 to a depth of 800 km.
The initial model had significant influence on the final model obtained by inversion. It suggested that the conductivity of the final model increased as the conductivity of the initial model increased [33,54]. A series of inversions with varied initial resistivity models and the same other parameters were performed. The initial model with a 100 Ωm resistivity had the lowest final RMS value of all the tests (Figure 6a). It was considered that the average apparent resistivity of all data points across all periods and sites was approximately 100 Ωm, and so the initial model was set to a 100-Ωm homogeneous half-space. According to the group of inversions with different smoothing factors (0.1, 0.2, 0.3, and 0.4), the smoothing factors were set to 0.4 for all three directions, because high smoothing factors were more pronounced for the features of high conductors in the lower crust and the high resistances in the shallow [33,54]. The initial value of the regularization parameter (λ) was set to 3000 and divided by 10 when the root mean square (RMS) changed minimally. After 207 iterations, the overall value of the RMS was reduced from 13.9 to 2.57. The site-by-site RMS (Figure 6b) and fitting comparison between observed and calculated data indicate that the final model results (Figure 7, Figure 8 and Figure 9) can be analyzed with a high degree of confidence.
The most promising feature of the final model was the presence of significant conductors across the entire crust. It was necessary to confirm the reliability of the high conductors through a sensitivity test [55]. These high conductors (C1, C2, and C3) in the final model were replaced with resistivity values of 1000 Ωm (Figure 10c). The forward calculation was carried out for each modified model to evaluate the robustness of high conductors. This was achieved by comparing them with the responses of the final and modified models after each sensitivity test. The modified model response data from site B02 deviated significantly from the measured MT data at periods greater than 0.1 s, and the sensitivity test results of C2 and C3 showed that the data deviation appeared at periods greater than 1 s and 10 s, respectively (Figure 10). These tests indicate that the high conductors (C1, C2, and C3) are essential to the final model, concluding that these conductors are reliable features and are derived from the measured MT data.
The final resistivity model (Figure 7, Figure 8 and Figure 9) correlated well with the known geological features of the near-surface region (Figure 3), indicating that the model accurately represents the shallow subsurface resistivity structure. High-resistance bodies greater than 1000 Ωm (R) in the upper crust correspond to typical values for Jurassic granite intrusions. There are three conductors (with resistivities less than 10 Ωm) surrounded by high-resistance intrusive rocks in the crust. The low resistance body (C1) in the shallow is interpreted as the fracture zone containing fluids, originating from meteoric water and infiltrating along the fault. The significant notable feature is that the upper crustal conductor (C2) cuts through the brittle ductile transition zone and connects with the lower crustal conductor (C3) beneath the Ganzi fault. Conductor C3 represents the fault fracture zone containing fluids or partial melting in the lower crustal flow.

5. Discussion

5.1. Conductors in the Crust

The most conspicuous feature in the final resistivity model is the presence of large-scale conductors extending through the crust beneath the Ganzi fault, which is consistent with the distribution of low-velocity bodies derived from seismological results (Figure 8) [56]. Possible explanations for these conductors in the crust include saline fluids, partial melt caused by high temperatures, solid-phase conduction by solid phases such as sulfide minerals, and graphite films [57,58]. According to the temperature model, the temperature of the upper crust is less than 600 °C [59], which is lower than the melting temperature of water-bearing granite [60]. Thus, the conductor C2 has been interpreted as interconnected saline fluids, possibly derived from either partial melting or metamorphism-induced dehydration. Pre-existing faults often act as fluid pathways, and both the reaction of hydrothermal fluids with rock and the local crustal extension caused by strike-slip faults trigger dynamic, permeable networks. Similar low-resistivity features related to fluids have been revealed in other large-scale strike-slip shear zones [28,34,61].
Lower crustal conductors revealed in other regions of the Eastern Tibetan Plateau have been interpreted as partial melt [37,42,46,62]. According to the high heat flow (greater than 90 mW/m2) [63] and temperature models [59] of the Eastern Tibetan Plateau, the temperature at a depth of 25 km in the thickened deep crust likely exceeds 700 °C, which is greater than the solidus of crustal rocks and is sufficient to trigger the partial melting of water-containing crustal rocks. There are low-velocity layers in the lower crust beneath the Ganzi fault, and the average crustal P wave to S wave velocity ratio value is high [56]. This suggests that the low-velocity characteristics of the layers in the lower crust may be because of partial melting caused by high temperatures. In addition, the material in the lower crust would be prone to plastic flow, facilitating the deformation and thickening of the crust. High Lg-wave attenuation has been acquired beneath the crust of the study regions [64], which may indicate the possible presence of partial melting within a relatively weak crust. Cenozoic granites within the Eastern Tibetan Plateau may have originated from crustal melting, as suggested by petrological studies [65]. Therefore, conductor C3 in the lower crust could be considered to be a broad zone of partial melting of the thickened crust. Laboratory measurements of the resistivity of hydrous granite melts further confirm crustal melting conditions beneath the Tibetan Plateau [66,67]. Considering that high conductors are dominated by partial melting, the partial melt fraction range of 7% to 16% is essential for explaining the typical bulk resistivity of 5 Ωm for conductor C3, according to the modified Archie’s law [68], and a pure melt resistivity of 0.1–0.3 Ωm [69].

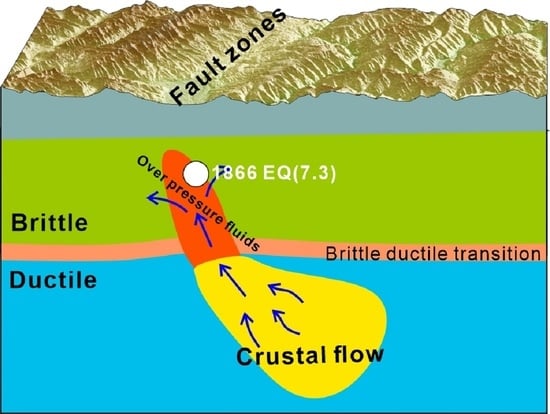
5.2. Role of Fluids in the Genesis of Earthquakes

The electrical resistivity model showed that the conductors beneath the Ganzi fault are closely related to deep fluids. The Ganzi region experienced low-grade metamorphism during the middle to late Triassic period [70], and it was difficult to generate a large amount of fluids during this metamorphism along the active fault compared with that generated in young high-grade metamorphism regions (such as Southern Alps orogen, New Zealand) [71]. Therefore, the fluid associated with the conductors is primarily released from the partial melting of the crustal flow, and tectonically-induced buoyancy promotes fluid upwards along the fault fracture zone. This accumulates in the upper crust above the brittle ductile transition [72]. The epicenter of the 1854 M7.5 earthquake occurred on the boundary region between the high-resistance body and the low-resistance body, near the high-resistive side at a depth of approximately 10 km along the Ganzi fault plane (Figure 8). This is consistent with the thermo-rheological structure of the region and the frequent occurrence of strong earthquakes along the boundaries of high and low resistivities [30,42,62,73]. Fluids play an important role in reducing rock strength by lowering the effective stresses across existing faults, promoting the growth of microcracks and pore interconnectivity, and causing mechanical weakening and hydrofracturing, which contribute to the generation of intraplate seismicity in the strike-slip shear region [25,74,75,76,77]. We propose that the genesis of intraplate earthquakes in the Ganzi region is controlled by fluid migration, and the Ganzi fault acts as an upwelling pathway from the lower crustal flow (Figure 11). Seismic ruptures in the crust are triggered by increases in fluid pressure [78], which are dependent on fluid volume changes generated by the decompression dehydration of partially molten material during upwelling and native fluid within the crustal flow. The Ganzi fault can cut through the brittle ductile transition, extend into the ductile regime, and enhance permeability through strike-slip fissures, which facilitates the upward migration of fluids [25]. Fluids accumulate in the crust above the brittle ductile transition under the far-field force from the collision of the Indian plate and the driving force generated by the difference of pressure within the crust [79]. Surrounding low-permeability rocks may act as a cap, which prevent the upward migration diffusion of fluids, creating overpressure fluids and enhancing seismic activity below them. Fluids and shear heating of the fault planes can effectively reduce the mechanical strength of the rock, which effects not only the fault planes but the entire rock volume [80]. The thermal activity of the lower crustal flow or the strike-slip activity of the fault increases the temperature of the overpressure fluids, which will inevitably lead to an increase in the pressure of the pore fluid to cause the mechanical rupture of the overlying brittle crust. This induces the occurrence of seismicity. Immediately after seismic rupture, both effective differential stress and fluid pressure will be reduced by fracture porosity and seismic stress release. Each individual seismic rupture would be followed by recovery that relies on reduction of the surrounding rock porosity and crack sealing due to stress redistribution and water-rock interactions [81]. The fluid pore pressure in the upper crust subsequently increases, accumulating force for the next seismic rupture during the inter-seismic period.

6. Conclusions

The heterogeneous crustal electrical structure beneath the Ganzi fault was obtained via 3D MT inversion. The most significant feature of this electrical structure is the presence of an assemblage of resistive and conductive features extending into the lower crust, reflecting the heterogeneity and complexity of the subsurface. The conductor in the brittle domain of the upper crust is interpreted as a fluid-rich fracture zone, with fluids from the partial melting of the lower crustal flow. The conductor in the lower crust is primarily caused by the partial melting of the crustal flow, and the partial melt fraction is estimated to be in the range of 7% to 16% using the modified Archie’s law. The epicenter of the earthquake was located at the edge of the upper crustal conductor, suggesting that the migration of fluids deriving from the crustal flow contributes to the initiation, growth, and arrest of intraplate earthquakes by increasing the effective fluid pore pressure and causing the mechanical rupture of the brittle crust.

Author Contributions

Conceptualization, Y.C., Y.K. and X.H.; validation, Z.W. and Y.H.; formal analysis, Y.C.; investigation, Y.C.; data curation, Y.C.; writing—original draft preparation, Y.C. and Y.K.; writing—review and editing, X.H.; visualization, Y.H.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China, grant number 42004060 and 42130809 and by the Chinese Academy of Sciences, grant number 2020-DX03-B-007.

Data Availability Statement

Not applicable.

Acknowledgments

We thank Gary Egbert and Anna Kelbert for providing the 3D MT inversion code Mod3DMT. We thank Yan Zhan (Institute of Geology, China Earthquake Administration) for providing the MT data of remote reference station. We would like to acknowledge Baoze Chao, Weixing Zhang, and Kangyun Wei for their support in collecting the field data. The work was carried out at the National Supercomputer Center in Tianjin, and the calculations were performed on TianHe-1(A). Several figures were plotted using the GMT software. We would like to thank three reviewers for constructive comments and insightful suggestions that have greatly improve the quality of the manuscripts.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Molnar, P.; Tapponnier, P. Cenozoic Tectonics of Asia: Effects of a Continental Collision. Science 1975, 189, 419–426. [Google Scholar] [CrossRef] [PubMed]
  2. Tapponnier, P.; Xu, Z.; Roger, F.; Meyer, B.; Arnaud, N.; Wittlinger, G.; Yang, J. Oblique Stepwise Rise and Growth of the Tibet Plateau. Science 2001, 294, 1671–1677. [Google Scholar] [CrossRef]
  3. Yin, A.; Harrison, T.M. Geologic Evolution of the Himalayan-Tibetan Orogen. Annu. Rev. Earth Planet. Sci. 2000, 28, 211–280. [Google Scholar] [CrossRef] [Green Version]
  4. Wang, C.; Zaho, X.; Liu, Z.; Lippert, P.; Graham, S.; Coe, R.; Yi, H.; Zhu, L.; Liu, S.; Li, Y. Constraints on the Early Uplift History of the Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2008, 105, 4987–4992. [Google Scholar] [CrossRef] [Green Version]
  5. Wang, E.; Burchfiel, B.C.; Royden, L.H.; Liangzhong, C.; Jishen, C.; Wenxin, L.; Zhiliang, C. Late Cenozoic Xianshuihe-Xiaojiang, Red River, and Dali Fault Systems of Southwestern Sichuan and Central Yunnan, China; Geological Society of America: Boulder, CO, USA, 1998; ISBN 9780813723273. [Google Scholar]
  6. Wang, E.; Burchfiel, B.C. Late Cenozoic to Holocene Deformation in Southwestern Sichuan and Adjacent Yunnan, China, and Its Role in Formation of the Southeastern Part of the Tibetan Plateau. Bull. Geol. Soc. Am. 2000, 112, 413–423. [Google Scholar] [CrossRef]
  7. Zhang, P.Z.; Molnar, P.; Xu, X. Late Quaternary and Present-Day Rates of Slip along the Altyn Tagh Fault, Northern Margin of the Tibetan Plateau. Tectonics 2007, 26, 1–24. [Google Scholar] [CrossRef] [Green Version]
  8. Allen, C.R.; Luo, Z.; Qian, H.; Wen, X.; Zhou, H.; Huang, W.; Zhuoli, L.; Hong, Q.; Xueze, W.; Huawei, Z.; et al. Field Study of a Highly Active Fault Zone: The Xianshuihe Fault of Southwestern China. Bull. Geol. Soc. Am. 1991, 103, 1178–1199. [Google Scholar] [CrossRef]
  9. Wang, S.; Fan, C.; Wang, G.; Wang, E. Late Cenozoic Deformation along the Northwestern Continuation of the Xianshuihe Fault System, Eastern Tibetan Plateau. Bull. Geol. Soc. Am. 2008, 120, 312–327. [Google Scholar] [CrossRef]
  10. Chevalier, M.-L.; Leloup, P.H.; Replumaz, A.; Pan, J.; Métois, M.; Li, H. Temporally Constant Slip Rate along the Ganzi Fault, NW Xianshuihe Fault System, Eastern Tibet. Bull. Geol. Soc. Am. 2017, 130, 396–410. [Google Scholar] [CrossRef]
  11. Zhang, P.Z.; Shen, Z.; Wang, M.; Gan, W.; Bürgmann, R.; Molnar, P.; Wang, Q.; Niu, Z.; Sun, J.; Wu, J.; et al. Continuous Deformation of the Tibetan Plateau from Global Positioning System Data. Geology 2004, 32, 809–812. [Google Scholar] [CrossRef]
  12. Gan, W.; Zhang, P.; Shen, Z.K.; Niu, Z.; Wang, M.; Wan, Y.; Zhou, D.; Cheng, J. Present-Day Crustal Motion within the Tibetan Plateau Inferred from GPS Measurements. J. Geophys. Res. Solid Earth 2007, 112, B08416. [Google Scholar] [CrossRef] [Green Version]
  13. Liang, S.; Gan, W.; Shen, C.; Xiao, G.; Liu, J.; Chen, W.; Ding, X.; Zhou, D. Three-Dimensional Velocity Field of Present-Day Crustal Motion of the Tibetan Plateau Derived from GPS Measurements. J. Geophys. Res. Solid Earth 2013, 118, 5722–5732. [Google Scholar] [CrossRef]
  14. Tapponnier, P.; Peltzer, G.; le Dain, A.Y.; Armijo, R.; Cobbold, P. Propagating Extrusion Tectonics in Asia: New Insights from Simple Experiments with Plasticine. Geology 1982, 10, 611–616. [Google Scholar] [CrossRef]
  15. Royden, L.H.; Burchfiel, B.C.; King, R.W.; Chen, Z.; Shen, F.; Liu, Y. Surface Deformation and Lower Crust Flow in Eastern Tibet. Science 1997, 276, 788–790. [Google Scholar] [CrossRef] [PubMed]
  16. Clark, M.K.; Royden, L.H. Topographic Ooze: Building the Eastern Margin of Tibet by Lower Crustal Flow. Geology 2000, 28, 703–706. [Google Scholar] [CrossRef]
  17. Wen, X.; Xu, X.; Zheng, R.; Xie, Y.; Wan, C. Average Slip-Rate and Recent Large Earthquake Ruptures along the Garzê-Yushu Fault. Sci. China Ser. D Earth Sci. 2003, 46, 276–288. [Google Scholar] [CrossRef]
  18. Li, A.; Shi, F.; Yang, X.; Xu, X. Recurrence of Paleoearthquakes on the Southeastern Segment of the Ganzi-Yushu Fault, Central Tibetan Plateau. Sci. China Earth Sci. 2013, 56, 165–172. [Google Scholar] [CrossRef]
  19. Huang, X.; Du, Y.; He, Z.; Ma, B.; Xie, F. Late Quaternary Slip Rate of the Batang Fault and Its Strain Partitioning Role in Yushu Area, Central Tibet. Tectonophysics 2015, 653, 52–67. [Google Scholar] [CrossRef]
  20. Shi, F.; He, H.; Densmore, A.L.; Li, A.; Yang, X.; Xu, X. Active Tectonics of the Ganzi-Yushu Fault in the Southeastern Tibetan Plateau. Tectonophysics 2016, 676, 112–124. [Google Scholar] [CrossRef] [Green Version]
  21. Chen, L.; Wang, H.; Ran, Y.; Sun, X.; Su, G.; Wang, J.; Tan, X.; Li, Z.; Zhang, X. The MS7.1 Yushu Earthquake Surface Rupture and Large Historical Earthquakes on the Garzê-Yushu Fault. Chinese Sci. Bull. 2010, 55, 3504–3509. [Google Scholar] [CrossRef]
  22. Shan, B.; Xiong, X.; Wang, R.; Zheng, Y.; Yang, S. Coulomb Stress Evolution along Xianshuihe-Xiaojiang Fault System since 1713 and Its Interaction with Wenchuan Earthquake, May 12, 2008. Earth Planet. Sci. Lett. 2013, 377–378, 199–210. [Google Scholar] [CrossRef] [Green Version]
  23. Wang, S.; Fang, X.; Zheng, D.; Wang, E. Initiation of Slip along the Xianshuihe Fault Zone, Eastern Tibet, Constrained by K/Ar and Fission-Track Ages. Int. Geol. Rev. 2009, 51, 1121–1131. [Google Scholar] [CrossRef]
  24. Chave, A.D.; Jones, A.G. The Magnetotelluric Method: Theory and Practice; Cambridge University Press: Cambridge, UK, 2012; ISBN 9781139020138. [Google Scholar]
  25. Wannamaker, P.E.; Jiracek, G.R.; Stodt, J.A.; Caldwell, T.G.; Gonzalez, V.M.; McKnight, J.D.; Porter, A.D. Fluid Generation and Pathways beneath an Active Compressional Orogen, the New Zealand Southern Alps, Inferred from Magnetotelluric Data. J. Geophys. Res. 2002, 107, ETG 6-1–ETG 6-20. [Google Scholar] [CrossRef] [Green Version]
  26. Wannamaker, P.E.; Caldwell, T.G.; Jiracek, G.R.; Maris, V.; Hill, G.J.; Ogawa, Y.; Bibby, H.M.; Bennie, S.L.; Heise, W. Fluid and Deformation Regime of an Advancing Subduction System at Marlborough, New Zealand. Nature 2009, 460, 733–736. [Google Scholar] [CrossRef] [PubMed]
  27. Ogawa, Y.; Ichiki, M.; Kanda, W.; Mishina, M.; Asamori, K. Three-Dimensional Magnetotelluric Imaging of Crustal Fluids and Seismicity around Naruko Volcano, NE Japan. Earth Planets Sp. 2014, 66, 1–13. [Google Scholar] [CrossRef] [Green Version]
  28. Becken, M.; Ritter, O.; Bedrosian, P.A.; Weckmann, U. Correlation between Deep Fluids, Tremor and Creep along the Central San Andreas Fault. Nature 2011, 480, 87–90. [Google Scholar] [CrossRef] [PubMed]
  29. Unsworth, M.J.; Jones, A.G.; Wei, W.; Marquis, G.; Gokarn, S.G.; Spratt, J.E.; Bedrosian, P.; Booker, J.; Leshou, C.; Clarke, G.; et al. Crustal Rheology of the Himalaya and Southern Tibet Inferred from Magnetotelluric Data. Nature 2005, 438, 78–81. [Google Scholar] [CrossRef] [PubMed]
  30. Cai, J.; Chen, X.; Xu, X.; Tang, J.; Wang, L.; Guo, C.; Han, B.; Dong, Z. Rupture Mechanism and Seismotectonics of the Ms6.5 Ludian Earthquake Inferred from Three-Dimensional Magnetotelluric Imaging. Geophys. Res. Lett. 2017, 44, 1275–1285. [Google Scholar] [CrossRef]
  31. Zhao, G.; Unsworth, M.J.; Zhan, Y.; Wang, L.; Chen, X.; Jones, A.G.; Tang, J.; Xiao, Q.; Wang, J.; Cai, J.; et al. Crustal Structure and Rheology of the Longmenshan and Wenchuan Mw 7.9 Earthquake Epicentral Area from Magnetotelluric Data. Geology 2012, 40, 1139–1142. [Google Scholar] [CrossRef]
  32. Siripunvaraporn, W. Three-Dimensional Magnetotelluric Inversion: An Introductory Guide for Developers and Users. Surv. Geophys. 2012, 33, 5–27. [Google Scholar] [CrossRef]
  33. Robertson, K.; Thiel, S.; Meqbel, N. Quality over Quantity: On Workflow and Model Space Exploration of 3D Inversion of MT Data. Earth Planets Sp. 2020, 72, 2. [Google Scholar] [CrossRef] [Green Version]
  34. Meqbel, N.; Weckmann, U.; Muñoz, G.; Ritter, O. Crustal Metamorphic Fluid Flux beneath the Dead Sea Basin: Constraints from 2-D and 3-D Magnetotelluric Modelling. Geophys. J. Int. 2016, 207, 1609–1629. [Google Scholar] [CrossRef]
  35. Egbert, G.D.; Kelbert, A. Computational Recipes for Electromagnetic Inverse Problems. Geophys. J. Int. 2012, 189, 251–267. [Google Scholar] [CrossRef] [Green Version]
  36. Siripunvaraporn, W.; Egbert, G.; Uyeshima, M. Interpretation of Two-Dimensional Magnetotelluric Profile Data with Three-Dimensional Inversion: Synthetic Examples. Geophys. J. Int. 2005, 160, 804–814. [Google Scholar] [CrossRef] [Green Version]
  37. Li, X.; Ma, X.; Chen, Y.; Xue, S.; Varentsov, I.M.; Bai, D. A Plume-Modified Lithospheric Barrier to the Southeastward Flow of Partially Molten Tibetan Crust Inferred from Magnetotelluric Data. Earth Planet. Sci. Lett. 2020, 548, 116493. [Google Scholar] [CrossRef]
  38. Yu, N.; Unsworth, M.; Wang, X.; Li, D.; Wang, E.; Li, R.; Hu, Y.; Cai, X. New Insights Into Crustal and Mantle Flow Beneath the Red River Fault Zone and Adjacent Areas on the Southern Margin of the Tibetan Plateau Revealed by a 3-D Magnetotelluric Study. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019396. [Google Scholar] [CrossRef]
  39. Yu, N.; Wang, E.; Wang, X.; Kong, W.; Li, D.; Li, R. The Influence of the Ailaoshan-Red River Shear Zone on the Mineralization of the Beiya Deposit on the Southeastern Margin of the Tibetan Plateau Revealed by a 3-D Magnetotelluric Survey. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022923. [Google Scholar] [CrossRef]
  40. Wang, X.; Zhang, G.; Fang, H.; Luo, W.; Zhang, W.; Zhong, Q.; Cai, X.; Luo, H. Crust and Upper Mantle Resistivity Structure at Middle Section of Longmenshan, Eastern Tibetan Plateau. Tectonophysics 2014, 619–620, 143–148. [Google Scholar] [CrossRef]
  41. Ye, T.; Huang, Q.; Chen, X.; Zhang, H.; Chen, Y.J.; Zhao, L.; Zhang, Y. Magma Chamber and Crustal Channel Flow Structures in the Tengchong Volcano Area From 3-D MT Inversion at the Intracontinental Block Boundary Southeast of the Tibetan Plateau. J. Geophys. Res. Solid Earth 2018, 123, 11–111. [Google Scholar] [CrossRef]
  42. Ye, T.; Chen, X.; Huang, Q.; Zhao, L.; Zhang, Y.; Uyeshima, M. Bifurcated Crustal Channel Flow and Seismogenic Structures of Intraplate Earthquakes in Western Yunnan, China as Revealed by Three-Dimensional Magnetotelluric Imaging. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018991. [Google Scholar] [CrossRef]
  43. Cheng, Y.; Tang, J.; Chen, X.; Dong, Z.; Xiao, Q.; Wang, L. Electrical Structure and Seismogenic Environment along the Border Region of Yunnan, Sichuan and Guizhou in the South of the North-South Seismic Belt. Chin. J. Geophys. 2015, 58, 3965–3981. [Google Scholar] [CrossRef]
  44. Cheng, Y.; Tang, J.; Cai, J.; Chen, X.; Dong, Z.; Wang, L. Deep Electrical Structure beneath the Sichuan-Yunnan Area in the Eastern Margin of the Tibetan Plateau. Chinese J. Geophys. 2017, 60, 2425–2441. [Google Scholar] [CrossRef]
  45. Li, X.; Bai, D.; Ma, X.; Chen, Y.; Varentsov, I.M.; Xue, G.; Xue, S.; Lozovsky, I. Electrical Resistivity Structure of the Xiaojiang Strike-Slip Fault System (SW China) and Its Tectonic Implications. J. Asian Earth Sci. 2019, 176, 57–67. [Google Scholar] [CrossRef]
  46. Bai, D.; Unsworth, M.J.; Meju, M.A.; Ma, X.; Teng, J.; Kong, X.; Sun, Y.; Sun, J.; Wang, L.; Jiang, C.; et al. Crustal Deformation of the Eastern Tibetan Plateau Revealed by Magnetotelluric Imaging. Nat. Geosci. 2010, 3, 358–362. [Google Scholar] [CrossRef]
  47. Di, Q.; Xue, G.; Zeng, Q.; Wang, Z.; An, Z.; Lei, D. Magnetotelluric Exploration of Deep-Seated Gold Deposits in the Qingchengzi Orefield, Eastern Liaoning (China), Using a SEP System. Ore Geol. Rev. 2020, 122, 103501. [Google Scholar] [CrossRef]
  48. Gamble, T.D.; Goubau, W.M.; Clarke, J. Magnetotellurics with a Remote Magnetic Reference. Geophysics 1979, 44, 53–68. [Google Scholar] [CrossRef] [Green Version]
  49. Jones, A.G.; Chave, A.D.; Egbert, G.; Auld, D.; Bahr, K. A Comparison of Techniques for Magnetotelluric Response Function Estimation. J. Geophys. Res. Solid Earth 1989, 94, 14201–14213. [Google Scholar] [CrossRef]
  50. Caldwell, T.G.; Bibby, H.M.; Brown, C. The Magnetotelluric Phase Tensor. Geophys. J. Int. 2004, 158, 457–469. [Google Scholar] [CrossRef] [Green Version]
  51. Hill, G.J.; Bibby, H.M.; Ogawa, Y.; Wallin, E.L.; Bennie, S.L.; Caldwell, T.G.; Keys, H.; Bertrand, E.A.; Heise, W. Structure of the Tongariro Volcanic System: Insights from Magnetotelluric Imaging. Earth Planet. Sci. Lett. 2015, 432, 115–125. [Google Scholar] [CrossRef]
  52. Egbert, G.D. Hybrid Conjugate Gradient-Occam Algorithms for Inversion of Multifrequency and Multitransmitter EM Data. Geophys. J. Int. 2012, 190, 255–266. [Google Scholar] [CrossRef] [Green Version]
  53. Kelbert, A.; Meqbel, N.; Egbert, G.D.; Tandon, K. ModEM: A Modular System for Inversion of Electromagnetic Geophysical Data. Comput. Geosci. 2014, 66, 40–53. [Google Scholar] [CrossRef]
  54. Li, X.; Chen, Y.; Tian, X.; Liu, S. Magnetotelluric Evidence for Distributed Lithospheric Modification Beneath the Yinchuan-Jilantai Rift System and Its Implications for Late Cenozoic Rifting in Western North China. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022585. [Google Scholar] [CrossRef]
  55. Tietze, K.; Ritter, O. Three-Dimensional Magnetotelluric Inversion in Practice-the Electrical Conductivity Structure of the San Andreas Fault in Central California. Geophys. J. Int. 2013, 195, 130–147. [Google Scholar] [CrossRef] [Green Version]
  56. Liu, Q.; van der Hilst, R.D.; Li, Y.; Yao, H.; Chen, J.; Guo, B.; Qi, S.; Wang, J.; Huang, H.; Li, S. Eastward Expansion of the Tibetan Plateau by Crustal Flow and Strain Partitioning across Faults. Nat. Geosci. 2014, 7, 361–365. [Google Scholar] [CrossRef]
  57. Jones, A.G. Imaging the Continental Upper Mantle Using Electromagnetic Methods. Lithos 1999, 48, 57–80. [Google Scholar] [CrossRef]
  58. Selway, K.; Yi, J.; Karato, S.I. Water Content of the Tanzanian Lithosphere from Magnetotelluric Data: Implications for Cratonic Growth and Stability. Earth Planet. Sci. Lett. 2014, 388, 175–186. [Google Scholar] [CrossRef]
  59. Sun, Y.; Dong, S.; Zhang, H.; Li, H.; Shi, Y. 3D Thermal Structure of the Continental Lithosphere beneath China and Adjacent Regions. J. Asian Earth Sci. 2013, 62, 697–704. [Google Scholar] [CrossRef]
  60. Puziewicz, J.; Johannes, W. Experimental Study of a Biotite-Bearing Granitic System under Water-Saturated and Water-Undersaturated Conditions. Contrib. Mineral. Petrol. 1990, 104, 397–406. [Google Scholar] [CrossRef]
  61. Unsworth, M.; Bedrosian, P.A. On the Geoelectric Structure of Major Strike-Slip Faults and Shear Zones. Earth Planets Sp. 2004, 56, 1177–1184. [Google Scholar] [CrossRef] [Green Version]
  62. Sun, X.; Zhan, Y.; Unsworth, M.; Egbert, G.; Zhang, H.; Chen, X.; Zhao, G.; Sun, J.; Zhao, L.; Cui, T.; et al. 3-D Magnetotelluric Imaging of the Easternmost Kunlun Fault: Insights Into Strain Partitioning and the Seismotectonics of the Jiuzhaigou Ms7.0 Earthquake. J. Geophys. Res. Solid Earth 2020, 125, 1–15. [Google Scholar] [CrossRef]
  63. Jiang, G.; Hu, S.; Shi, Y.; Zhang, C.; Wang, Z.; Hu, D. Terrestrial Heat Flow of Continental China: Updated Dataset and Tectonic Implications. Tectonophysics 2019, 753, 36–48. [Google Scholar] [CrossRef]
  64. Zhao, L.F.; Xie, X.B.; He, J.K.; Tian, X.; Yao, Z.X. Crustal Flow Pattern beneath the Tibetan Plateau Constrained by Regional Lg-Wave Q Tomography. Earth Planet. Sci. Lett. 2013, 383, 113–122. [Google Scholar] [CrossRef]
  65. Roger, F.; Calassou, S.; Lancelot, J.; Malavieille, J.; Mattauer, M.; Xu, Z.; Hao, Z.; Hou, L. Miocene Emplacement and Deformation of the Konga Shan Granite (Xianshui He Fault Zone, West Sichuan, China): Geodynamic Implications. Earth Planet. Sci. Lett. 1995, 130, 201–216. [Google Scholar] [CrossRef]
  66. Gaillard, F.; Scaillet, B.; Pichavant, M. Evidence for Present-Day Leucogranite Pluton Growth in Tibet. Geology 2004, 32, 801–804. [Google Scholar] [CrossRef] [Green Version]
  67. Chen, J.; Gaillard, F.; Villaros, A.; Yang, X.; Laumonier, M.; Jolivet, L.; Unsworth, M.; Hashim, L.; Scaillet, B.; Richard, G. Melting Conditions in the Modern Tibetan Crust since the Miocene. Nat. Commun. 2018, 9, 3515. [Google Scholar] [CrossRef]
  68. Glover, P.W.J.; Hole, M.J.; Pous, J. A Modified Archie’s Law for Two Conducting Phases. Earth Planet. Sci. Lett. 2000, 180, 369–383. [Google Scholar] [CrossRef]
  69. Li, S.; Unsworth, M.J.; Booker, J.R.; Wei, W.; Tan, H.; Jones, A.G. Partial Melt or Aqueous Fluid in the Mid-Crust of Southern Tibet? Constraints from INDEPTH Magnetotelluric Data. Geophys. J. Int. 2003, 153, 289–304. [Google Scholar] [CrossRef] [Green Version]
  70. Enkelmann, E.; Weislogel, A.; Ratschbacher, L.; Eide, E.; Renno, A.; Wooden, J. How Was the Triassic Songpan-Ganzi Basin Filled? A Provenance Study. Tectonics 2007, 26. [Google Scholar] [CrossRef] [Green Version]
  71. Vry, J.K.; Storkey, A.C.; Harris, C. Role of Fluids in the Metamorphism of the Alpine Fault Zone, New Zealand. J. Metamorph. Geol. 2001, 19, 21–31. [Google Scholar] [CrossRef]
  72. Connolly, J.A.D.; Podladchikov, Y.Y. Fluid Flow in Compressive Tectonic Settings: Implications for Midcrustal Seismic Reflectors and Downward Fluid Migration. J. Geophys. Res. Solid Earth 2004, 109, B04201. [Google Scholar] [CrossRef]
  73. Chen, L.; Berntsson, F.; Zhang, Z.; Wang, P.; Wu, J.; Xu, T. Seismically Constrained Thermo-Rheological Structure of the Eastern Tibetan Margin: Implication for Lithospheric Delamination. Tectonophysics 2014, 627, 122–134. [Google Scholar] [CrossRef]
  74. Ogawa, Y.; Mishina, M.; Goto, T.; Satoh, H.; Oshiman, N.; Kasaya, T.; Takahashi, Y.; Nishitani, T.; Sakanaka, S.; Uyeshima, M.; et al. Magnetotelluric Imaging of Fluids in Intraplate Earthquake Zones, NE Japan Back Arc. Geophys. Res. Lett. 2001, 28, 3741–3744. [Google Scholar] [CrossRef]
  75. Pavan Kumar, G.; Mahesh, P.; Nagar, M.; Mahender, E.; Kumar, V.; Mohan, K.; Ravi Kumar, M. Role of Deep Crustal Fluids in the Genesis of Intraplate Earthquakes in the Kachchh Region, Northwestern India. Geophys. Res. Lett. 2017, 44, 4054–4063. [Google Scholar] [CrossRef]
  76. Tang, Y.; Weng, A.; Yang, Y.; Li, S.; Niu, J.; Zhang, Y.; Li, Y.; Li, J. Connection between Earthquakes and Deep Fluids Revealed by Magnetotelluric Imaging in Songyuan, China. Sci. China Earth Sci. 2021, 64, 161–176. [Google Scholar] [CrossRef]
  77. Li, D.; Yu, N.; Li, X.; Wang, E.; Li, R.; Wang, X. Magnetotelluric Evidence of Fluid-Related Seismicity beneath the Chuxiong Basin, SE Tibetan Plateau. Tectonophysics 2021, 816, 229039. [Google Scholar] [CrossRef]
  78. Chapman, T.; Milan, L.; Vry, J. The Role of Metamorphic Fluid in Tectonic Tremor Along the Alpine Fault, New Zealand. Geophys. Res. Lett. 2022, 49, e2021GL096415. [Google Scholar] [CrossRef]
  79. Wang, Z.; Wang, J.; Yang, X. The Role of Fluids in the 2008 Ms8.0 Wenchuan Earthquake, China. J. Geophys. Res. Solid Earth 2021, 126, e2020JB019959. [Google Scholar] [CrossRef]
  80. Segall, P.; Rice, J.R. Does Shear Heating of Pore Fluid Contribute to Earthquake Nucleation? J. Geophys. Res. Solid Earth 2006, 111, B09316. [Google Scholar] [CrossRef] [Green Version]
  81. Gratier, J.-P.; Favreau, P.; Renard, F.; Pili, E. Fluid Pressure Evolution during the Earthquake Cycle Controlled by Fluid Flow and Pressure Solution Crack Sealing. Earth Planets Sp. 2002, 54, 1139–1146. [Google Scholar] [CrossRef] [Green Version]
Remotesensing 14 02990 g001 550
Figure 1. (a) Tectonic map of the Tibetan Plateau with topographic relief. (b) Digital elevation map of the Ganzi fault region with active faults in red, main rivers in blue, and historical earthquakes in white circles. GZ, Ganzi; EZ, Ezhi; BT, Batang; XSHF, Xianshuihe fault; GF, Ganzi fault.
Figure 1. (a) Tectonic map of the Tibetan Plateau with topographic relief. (b) Digital elevation map of the Ganzi fault region with active faults in red, main rivers in blue, and historical earthquakes in white circles. GZ, Ganzi; EZ, Ezhi; BT, Batang; XSHF, Xianshuihe fault; GF, Ganzi fault.
Remotesensing 14 02990 g001
Remotesensing 14 02990 g002 550
Figure 2. Flow diagram showing major parts of the standard processing steps for MT data.
Figure 2. Flow diagram showing major parts of the standard processing steps for MT data.
Remotesensing 14 02990 g002
Remotesensing 14 02990 g003 550
Figure 3. Geological structure map of the study region with topographic relief and magnetotelluric sites indicated as purple triangles. The blue solid and dotted line represents fault.
Figure 3. Geological structure map of the study region with topographic relief and magnetotelluric sites indicated as purple triangles. The blue solid and dotted line represents fault.
Remotesensing 14 02990 g003
Remotesensing 14 02990 g004 550
Figure 4. Observed (triangles) and calculated (solid lines) apparent resistivities and phase curves at nine typical MT sites. The red triangles and solid lines represent the XY-mode, and the blue triangles and solid lines represent YX-mode data in the observation coordinate system. The X-axis is aligned with the geomagnetic north.
Figure 4. Observed (triangles) and calculated (solid lines) apparent resistivities and phase curves at nine typical MT sites. The red triangles and solid lines represent the XY-mode, and the blue triangles and solid lines represent YX-mode data in the observation coordinate system. The X-axis is aligned with the geomagnetic north.
Remotesensing 14 02990 g004
Remotesensing 14 02990 g005 550
Figure 5. Pseudo-sections of normalized phase tensor ellipses with the values of β (a,c) and Φ1 (b,d) as a function of the period for all periods and sites along two profiles. Each ellipse denotes the phase tensor for a single period at a single MT site.
Figure 5. Pseudo-sections of normalized phase tensor ellipses with the values of β (a,c) and Φ1 (b,d) as a function of the period for all periods and sites along two profiles. Each ellipse denotes the phase tensor for a single period at a single MT site.
Remotesensing 14 02990 g005
Remotesensing 14 02990 g006 550
Figure 6. (a) The final root mean square (RMS) misfit of the inversion with various initial resistivities (10, 20, 50, 100, 200, 500, and 1000 Ωm). (b) Map of the site with RMS misfits in the final 3D inversion with the initial resistivity model of 100 Ωm.
Figure 6. (a) The final root mean square (RMS) misfit of the inversion with various initial resistivities (10, 20, 50, 100, 200, 500, and 1000 Ωm). (b) Map of the site with RMS misfits in the final 3D inversion with the initial resistivity model of 100 Ωm.
Remotesensing 14 02990 g006
Remotesensing 14 02990 g007 550
Figure 7. The final model at representative depth slices. The black triangles denote the MT sites, and the white lines denote active faults. The black lines denote MT profiles in Figure 8. The conductive anomalies (C1–C3) are discussed in this paper.
Figure 7. The final model at representative depth slices. The black triangles denote the MT sites, and the white lines denote active faults. The black lines denote MT profiles in Figure 8. The conductive anomalies (C1–C3) are discussed in this paper.
Remotesensing 14 02990 g007
Remotesensing 14 02990 g008 550
Figure 8. (a,b) Topography along the MT profiles. (c,d) Cross-section with the MT sites (triangles on top of the panel) extracted from the final model along the MT profiles (Lines AA’ and BB’ in Figure 7f). The red and black solid line represents fault. The white circle represents the epicenter of the 1866 M7.3 earthquake. (e) P (blue line) and S (red line) wave velocity structures beneath the seismic site (red triangle in Figure 3) [56].
Figure 8. (a,b) Topography along the MT profiles. (c,d) Cross-section with the MT sites (triangles on top of the panel) extracted from the final model along the MT profiles (Lines AA’ and BB’ in Figure 7f). The red and black solid line represents fault. The white circle represents the epicenter of the 1866 M7.3 earthquake. (e) P (blue line) and S (red line) wave velocity structures beneath the seismic site (red triangle in Figure 3) [56].
Remotesensing 14 02990 g008
Remotesensing 14 02990 g009 550
Figure 9. The 3D model displayed with the 10 Ωm isosurface. The yellow isosurface represents the isosurface of 10 Ωm. This model reveals three conductors in the crust (C1–C3). MT sites are indicated as black triangles. High conductors C2 and C3 connect to the lower crust.
Figure 9. The 3D model displayed with the 10 Ωm isosurface. The yellow isosurface represents the isosurface of 10 Ωm. This model reveals three conductors in the crust (C1–C3). MT sites are indicated as black triangles. High conductors C2 and C3 connect to the lower crust.
Remotesensing 14 02990 g009
Remotesensing 14 02990 g010 550
Figure 10. The revised model for the sensitivity test (c), and the results of sensitivity test (a,b,d). The triangles denote the measured MT data, the dashed lines denote calculated data from the final model, and the solid lines indicate calculated data from the revised model. The MT sites are shown as red solid triangles on the top of the revised model.
Figure 10. The revised model for the sensitivity test (c), and the results of sensitivity test (a,b,d). The triangles denote the measured MT data, the dashed lines denote calculated data from the final model, and the solid lines indicate calculated data from the revised model. The MT sites are shown as red solid triangles on the top of the revised model.
Remotesensing 14 02990 g010
Remotesensing 14 02990 g011 550
Figure 11. Schematic diagram interpretation of resistivity features related to fluid migration in the crust. Blue arrows indicate the upward migration of fluids originating from the lower crustal flow through fault fracture (black lines) and accumulation in the upper crust to form overpressure fluids. BDT represents brittle ductile transition. The red arrow indicates the shearing directions inferred from geologic and geodetic observations at the surface.
Figure 11. Schematic diagram interpretation of resistivity features related to fluid migration in the crust. Blue arrows indicate the upward migration of fluids originating from the lower crustal flow through fault fracture (black lines) and accumulation in the upper crust to form overpressure fluids. BDT represents brittle ductile transition. The red arrow indicates the shearing directions inferred from geologic and geodetic observations at the surface.
Remotesensing 14 02990 g011
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Cheng, Y.; Kong, Y.; Wang, Z.; Huang, Y.; Hu, X. Crustal Electrical Structure of the Ganzi Fault on the Eastern Tibetan Plateau: Implications for the Role of Fluids in Earthquakes. Remote Sens. 2022, 14, 2990. https://doi.org/10.3390/rs14132990

AMA Style

Cheng Y, Kong Y, Wang Z, Huang Y, Hu X. Crustal Electrical Structure of the Ganzi Fault on the Eastern Tibetan Plateau: Implications for the Role of Fluids in Earthquakes. Remote Sensing. 2022; 14(13):2990. https://doi.org/10.3390/rs14132990

Chicago/Turabian Style

Cheng, Yuanzhi, Yanlong Kong, Zhongxing Wang, Yonghui Huang, and Xiangyun Hu. 2022. "Crustal Electrical Structure of the Ganzi Fault on the Eastern Tibetan Plateau: Implications for the Role of Fluids in Earthquakes" Remote Sensing 14, no. 13: 2990. https://doi.org/10.3390/rs14132990

APA Style

Cheng, Y., Kong, Y., Wang, Z., Huang, Y., & Hu, X. (2022). Crustal Electrical Structure of the Ganzi Fault on the Eastern Tibetan Plateau: Implications for the Role of Fluids in Earthquakes. Remote Sensing, 14(13), 2990. https://doi.org/10.3390/rs14132990

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop