Evaluation of Albedo Schemes in WRF Coupled with Noah-MP on the Parlung No. 4 Glacier
Abstract
:1. Introduction
2. Data and Methodology
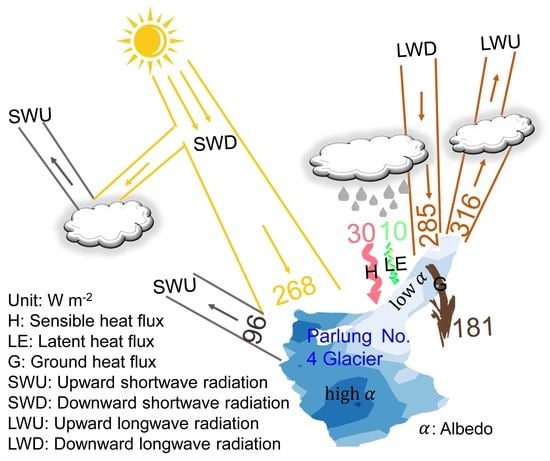
2.1. Study Area and In-Situ Measurements
2.2. Model Configuration and Experimental Design
2.3. Evaluation of Model Performance
3. Results
3.1. Air Temperature and Precipitation
3.2. Net Radiation Flux and Albedo
3.3. Turbulent Heat Flux
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qiu, J. The third pole. Nature 2008, 454, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Robinson, D.A. Hemispheric snow cover and surface albedo for model validation. Ann. Glaciol. 1997, 25, 241–245. [Google Scholar] [CrossRef]
- Bamzai, A.S.; Shukla, J. Relation between Eurasian snow cover, snow depth, and the Indian summer monsoon: An observational study. J. Clim. 1999, 12, 3117–3132. [Google Scholar] [CrossRef]
- Zemp, M.; Roer, I.; Kääb, A.; Hoelzle, M.; Paul, F.; Haeberli, W. Global Glacier Changes: Facts and Figures; World Glacier Monitoring Service: Zürich, Switzerland, 2008. [Google Scholar]
- Davaze, L.; Rabatel, A.; Dufour, A.; Hugonnet, R.; Arnaud, Y. Region-Wide Annual Glacier Surface Mass Balance for the European Alps from 2000 to 2016. Front. Earth Sci. 2020, 8, 149. [Google Scholar] [CrossRef]
- Fujita, K.; Ageta, Y. Effect of summer accumulation on glacier mass balance on the Tibetan Plateau revealed by mass-balance model. J. Glaciol. 2000, 46, 244–252. [Google Scholar] [CrossRef]
- Fujita, K.; Ageta, Y.; Pu, J.; Yao, T. Mass balance of Xiao Dongkemadi glacier on the central Tibetan Plateau from 1989 to 1995. Ann. Glaciol. 2000, 31, 159–163. [Google Scholar] [CrossRef]
- Cogley, J.G. Climate science: Himalayan glaciers in the balance. Nature 2012, 488, 468–469. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef]
- Ding, B.; Yang, K.; Yang, W.; He, X.; Chen, Y.; La, Z.; Guo, X.; Wang, L.; Wu, H.; Yao, T. Development of a Water and Enthalpy Budget-based Glacier mass balance Model (WEB-GM) and its preliminary validation. Water Resour. Res. 2017, 53, 3146–3178. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, S.; Li, J.; Shangguan, D. The retreat of glaciers in response to recent climate warming in western China. Ann. Glaciol. 2006, 43, 97–105. [Google Scholar] [CrossRef]
- Kang, S.; Qin, D.; Ren, J.; Zhang, Y.; Kaspari, S.; Mayewski, P.A.; Hou, S. Annual accumulation in the Mt. nyainqentanglha ice core, southern Tibetan plateau, China: Relationships to atmospheric circulation over Asia. Arct. Antarct. Alp. Res. 2007, 39, 663–670. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Jin, H.; Kang, E.; Che, T.; Jin, R.; Wu, L.; Nan, Z.; Wang, J.; Shen, Y. Cryospheric change in China. Glob. Planet. Change 2008, 62, 210–218. [Google Scholar] [CrossRef]
- Yao, T.; Wang, Y.; Liu, S.; Pu, J.; Shen, Y.; Lu, A. Recent glacial retreat in High Asia in China and its impact on water resource in Northwest China. Sci. China Ser. D-Earth Sci. 2004, 47, 1065–1075. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Change 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Yao, T.; Pu, J.; Lu, A.; Wang, Y.; Yu, W. Recent glacial retreat and its impact on hydrological processes on the tibetan plateau, China, and sorrounding regions. Arct. Antarct. Alp. Res. 2007, 39, 642–650. [Google Scholar] [CrossRef]
- Meier, M.F.; Dyurgerov, M.B.; Rick, U.K.; O’neel, S.; Pfeffer, W.T.; Anderson, R.S.; Anderson, S.P.; Glazovsky, A.F. Glaciers dominate Eustatic sea-level rise in the 21st century. Science 2007, 317, 1064–1067. [Google Scholar] [CrossRef] [PubMed]
- Hock, R.; De Woul, M.; Radic, V.; Dyurgerov, M. Mountain glaciers and ice caps around Antarctica make a large sea-level rise contribution. Geophys. Res. Lett. 2009, 36, L07501. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef]
- Yang, W.; Guo, X.; Yao, T.; Yang, K.; Zhao, L.; Li, S.; Zhu, M. Summertime surface energy budget and ablation modeling in the ablation zone of a maritime Tibetan glacier. J. Geophys. Res. Atmos. 2011, 116, D14116. [Google Scholar] [CrossRef]
- Yang, W.; Yao, T.; Guo, X.; Zhu, M.; Li, S.; Kattel, D.B. Mass balance of a maritime glacier on the southeast Tibetan Plateau and its climatic sensitivity. J. Geophys. Res. Atmos. 2013, 118, 9579–9594. [Google Scholar] [CrossRef]
- Yang, W.; Yao, T.; Zhu, M.; Wang, Y. Comparison of the meteorology and surface energy fluxes of debris-free and debris-covered glaciers in the southeastern Tibetan Plateau. J. Glaciol. 2017, 63, 1090–1104. [Google Scholar] [CrossRef]
- Zhu, M.; Yao, T.; Yang, W.; Maussion, F.; Huintjes, E.; Li, S. Energy- and mass-balance comparison between Zhadang and Parlung No. 4 glaciers on the Tibetan Plateau. J. Glaciol. 2015, 61, 595–607. [Google Scholar]
- Mölg, T.; Maussion, F.; Scherer, D. Mid-latitude westerlies as a driver of glacier variability in monsoonal High Asia. Nat. Clim. Change 2014, 4, 68. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.; et al. A Description of the Advanced Research WRF Model Version 4.3; (No. NCAR/TN-556+STR); National Center for Atmospheric Research: Boulder, CO, USA, 2021. [Google Scholar] [CrossRef]
- Mölg, T.; Kaser, G. A new approach to resolving climate-cryosphere relations: Downscaling climate dynamics to glacier-scale mass and energy balance without statistical scale linking. J. Geophys. Res. Atmos. 2011, 116, D16101. [Google Scholar] [CrossRef]
- Collier, E.; Mölg, T.; Maussion, F.; Scherer, D.; Mayer, C.; Bush, A.B.G. High-resolution interactive modelling of the mountain glacier-atmosphere interface: An application over the Karakoram. Cryosphere 2013, 7, 779–795. [Google Scholar] [CrossRef]
- Collier, E.; Maussion, F.; Nicholson, L.I.; Molg, T.; Immerzeel, W.W.; Bush, A.B.G. Impact of debris cover on glacier ablation and atmosphere-glacier feedbacks in the Karakoram. Cryosphere 2015, 9, 1617–1632. [Google Scholar] [CrossRef]
- Bonekamp, P.N.J.; Collier, E.; Immerzeel, W.W. The Impact of Spatial Resolution, Land Use, and Spinup Time on Resolving Spatial Precipitation Patterns in the Himalayas. J. Hydrometeorol. 2018, 19, 1565–1581. [Google Scholar] [CrossRef]
- Bonekamp, P.N.J.; De Kok, R.J.; Collier, E.; Immerzeel, W.W. Contrasting Meteorological Drivers of the Glacier Mass Balance Between the Karakoram and Central Himalaya. Front. Earth Sci. 2019, 7, 107. [Google Scholar] [CrossRef]
- Mölg, T.; Maussion, F.; Yang, W.; Scherer, D. The footprint of Asian monsoon dynamics in the mass and energy balance of a Tibetan glacier. Cryosphere 2012, 6, 1445–1461. [Google Scholar] [CrossRef]
- Aas, K.S.; Dunse, T.; Collier, E.; Schuler, T.V.; Berntsen, T.K.; Kohler, J.; Luks, B. The climatic mass balance of Svalbard glaciers: A 10-year simulation with a coupled atmosphere-glacier mass balance model. Cryosphere 2016, 10, 1089–1104. [Google Scholar] [CrossRef]
- Pirazzini, R. Challenges in Snow and Ice Albedo Parameterizations. Geophysica 2009, 45, 41–62. [Google Scholar]
- Mölders, N.; Luijting, H.; Sassen, K. Use of atmospheric radiation measurement program data from Barrow, Alaska, for evaluation and development of snow-albedo parameterizations. Meteorol. Atmos. Phys. 2008, 99, 199–219. [Google Scholar] [CrossRef]
- Oerlemans, J.; Knap, W.H. A 1 year record of global radiation and albedo in the ablation zone of Morteratschgletscher, Switzerland. J. Glaciol. 1998, 44, 231–238. [Google Scholar] [CrossRef]
- Pedersen, C.A.; Winther, J.G. Intercomparison and validation of snow albedo parameterization schemes in climate models. Clim. Dyn. 2005, 25, 351–362. [Google Scholar] [CrossRef]
- Schmidt, L.S.; Aðalgeirsdóttir, G.; Guðmundsson, S.; Langen, P.L.; Pálsson, F.; Mottram, R.; Gascoin, S.; Björnsson, H. The importance of accurate glacier albedo for estimates of surface mass balance on Vatnajökull: Evaluating the surface energy budget in a regional climate model with automatic weather station observations. Cryosphere 2017, 11, 1665–1684. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Henderson-Sellers, A.; Kennedy, P.J. Biosphere-Atmosphere Transfer Scheme (BATS) Version le as Coupled to the NCAR Community Climate Model; Tech. Rep. NCAR/TN-387+STR; National Center for Atmospheric Research: Boulder, CO, USA, 1993; 174p. [Google Scholar]
- Bonan, G.B. A Land Surface Model (LSM Version 1.0) for Ecological, Hydrological, and Atmospheric Studies: Technical Description and User’s Guide; Tech. Rep. NCAR/TN-417+STR; National Center for Atmospheric Research: Boulder, CO, USA, 1996; 150p. [Google Scholar]
- Warren, S.G.; Wiscombe, W.J. A Model for the Spectral Albedo of Snow. II: Snow Containing Atmospheric Aerosols. J. Atmos. Sci. 1980, 37, 2734–2745. [Google Scholar] [CrossRef]
- Willeit, M.; Ganopolski, A. The importance of snow albedo for ice sheet evolution over the last glacial cycle. Clim. Past 2018, 14, 697–707. [Google Scholar] [CrossRef]
- Usha, K.H.; Nair, V.S.; Babu, S.S. Modeling of aerosol induced snow albedo feedbacks over the Himalayas and its implications on regional climate. Clim. Dyn. 2020, 54, 4191–4210. [Google Scholar] [CrossRef]
- Arndt, A.; Scherer, D.; Schneider, C. Atmosphere Driven Mass-Balance Sensitivity of Halji Glacier, Himalayas. Atmosphere 2021, 12, 426. [Google Scholar] [CrossRef]
- Berrisford, P.; Dee, D.P.; Poli, P.; Brugge, R.; Fielding, K.; Fuentes, M.; Kallberg, P.W.; Kobayashi, S.; Uppala, S.; Simmons, A. The ERA-interim Archive Version 2.0; European Centre for Medium Range Weather Forecasts: Reading, UK, 2011. [Google Scholar]
- Liu, L.; Gu, H.; Xie, J.; Xu, Y. How well do the ERA-Interim, ERA-5, GLDAS-2.1 and NCEP-R2 reanalysis datasets represent daily air temperature over the Tibetan Plateau? Int. J. Climatol. 2021, 41, 1484–1505. [Google Scholar] [CrossRef]
- Niu, G.; Yang, Z.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef]
- Yang, Z.; Niu, G.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Longuevergne, L.; Manning, K.; Niyogi, D.; Tewari, M.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 2. Evaluation over global river basins. J. Geophys. Res. Atmos. 2011, 116, D12110. [Google Scholar] [CrossRef]
- Niu, G.; Yang, Z. The effects of canopy processes on snow surface energy and mass balance. J. Geophys. Res. Atmos. 2004, 109, D23111. [Google Scholar] [CrossRef]
- Liu, L.; Ma, Y.; Menenti, M.; Zhang, X.; Ma, W. Evaluation of WRF Modeling in Relation to Different Land Surface Schemes and Initial and Boundary Conditions: A Snow Event Simulation Over the Tibetan Plateau. J. Geophys. Res. Atmos. 2019, 124, 209–226. [Google Scholar] [CrossRef]
- Vose, R.S.; Karl, T.R.; Easterling, D.R.; Williams, C.N.; Menne, M.J. Climate—Impact of land-use change on climate. Nature 2004, 427, 213–214. [Google Scholar] [CrossRef]
- Verseghy, D.L. Class-A Canadian land surface scheme for GCMS. I. Soil model. Int. J. Climatol. 1991, 11, 111–133. [Google Scholar] [CrossRef]
- Naegeli, K.; Damm, A.; Huss, M.; Wulf, H.; Schaepman, M.; Hoelzle, M. Cross-Comparison of Albedo Products for Glacier Surfaces Derived from Airborne and Satellite (Sentinel-2 and Landsat 8) Optical Data. Remote Sens. 2017, 9, 110. [Google Scholar] [CrossRef]
- Yang, Z.; Cai, X.; Zhang, G.; Tavakoly, A.A.; Jin, Q.; Meyer, L.H.; Guan, X. The Community Noah Land Surface Model with Multi-Parameterization Options (Noah-MP). Technical Description. 2011. Available online: https://www.jsg.utexas.edu/noah-mp/downloads/ (accessed on 1 January 2022).
- Dadic, R.; Mullen, P.C.; Schneebeli, M.; Brandt, R.E.; Warren, S.G. Effects of bubbles, cracks, and volcanic tephra on the spectral albedo of bare ice near the Transantarctic Mountains: Implications for sea glaciers on Snowball Earth. J. Geophys. Res. Earth Surf. 2013, 118, 1658–1676. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to Broadband conversions of land surface albedo: I. Algorithms. Remote Sens. Environ. 2000, 76, 213–238. [Google Scholar] [CrossRef]
- Gou, J.; Wang, F.; Jin, K.; Mu, X.; Chen, D. More realistic land-use and vegetation parameters in a regional climate model reduce model biases over China. Int. J. Climatol. 2019, 39, 4825–4837. [Google Scholar] [CrossRef]







| Simulations Time Period | From 1 May to 1 October 2016 |
|---|---|
| Nest | Three nested domains (two-way) |
| Projection | Mercator |
| Center of domain | 29.23°N, 96.92°E |
| Resolution | 12.5 km, 2.5 km, 0.5 km |
| Microphysics | Thompson scheme |
| Longwave radiation | RRTM scheme |
| Shortwave radiation | Dudhia scheme |
| Surface layer | Revised MM5 Monin-Obukhov scheme |
| Planetary boundary layer | YSU scheme |
| Cumulus parameterization | Grell-Devenyi ensemble scheme in domain 1 |
| Land surface | Noah-MP |
| Canopy stomatal resistance | Ball-Berry scheme |
| Soil moisture factor for stomatal resistance | Noah scheme |
| Runoff and groundwater | TOPMODEL with groundwater |
| Surface layer drag coefficient | Monin–Obukhov |
| Soil permeability option | Linear effect, more permeable |
| Radiation transfer | Two-stream applied to vegetated fraction |
| Ground surface albedo option | CLASS (Canadian Land Surface Scheme) |
| Precipitation partitioning between snow and rain | Jordan scheme |
| Snow/soil temperature time scheme | Semi-implicit |
| Noah-MP glacier treatment | Includes phase change |
| Experiment | Land-Use Categories | Vegetation Fraction/% | Soil Categories | Background Albedo | Bare Ice Albedo | Snow Albedo Scheme |
|---|---|---|---|---|---|---|
| CTL | open shrub-land | 30.5 | loam | 0.16 | - | CLASS |
| Sens1 | snow and ice | 0 | land-ice | 0.55 | vis = 0.8, nir = 0.55 | CLASS |
| Sens2 | snow and ice | 0 | land-ice | 0.23 | vis = 0.5, nir = 0.2 | combined CLASS and BATS |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Menenti, M.; Ma, Y. Evaluation of Albedo Schemes in WRF Coupled with Noah-MP on the Parlung No. 4 Glacier. Remote Sens. 2022, 14, 3934. https://doi.org/10.3390/rs14163934
Liu L, Menenti M, Ma Y. Evaluation of Albedo Schemes in WRF Coupled with Noah-MP on the Parlung No. 4 Glacier. Remote Sensing. 2022; 14(16):3934. https://doi.org/10.3390/rs14163934
Chicago/Turabian StyleLiu, Lian, Massimo Menenti, and Yaoming Ma. 2022. "Evaluation of Albedo Schemes in WRF Coupled with Noah-MP on the Parlung No. 4 Glacier" Remote Sensing 14, no. 16: 3934. https://doi.org/10.3390/rs14163934
APA StyleLiu, L., Menenti, M., & Ma, Y. (2022). Evaluation of Albedo Schemes in WRF Coupled with Noah-MP on the Parlung No. 4 Glacier. Remote Sensing, 14(16), 3934. https://doi.org/10.3390/rs14163934