Next Article in Journal
Assessing the Impact of Urbanization and Eco-Environmental Quality on Regional Carbon Storage: A Multiscale Spatio-Temporal Analysis Framework
Next Article in Special Issue
Automatic Detection of the Explosive Activity of the Mt. Etna Volcano through Doppler Radar Monitoring
Previous Article in Journal
Outlier-Robust Truncated Maximum Likelihood Parameter Estimation of Compound-Gaussian Clutter with Inverse Gaussian Texture
Previous Article in Special Issue
Remote Sensing and Mineralogical Analyses: A First Application to the Highly Active Hydrothermal Discharge Area of Pisciarelli in the Campi Flegrei Volcanic Field (Italy)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 16
10.3390/rs14164006
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Explosive Paroxysmal Events at Etna Volcano of Different Magnitude and Intensity Explored through a Multidisciplinary Monitoring System

by
Sonia Calvari
1,*,
Emilio Biale
1,
Alessandro Bonaccorso
1,
Andrea Cannata
1,2,
Luigi Carleo
1,
Gilda Currenti
1,
Giuseppe Di Grazia
1,
Gaetana Ganci
1,
Adriana Iozzia
1,2,
Emilio Pecora
1,
Michele Prestifilippo
1,
Mariangela Sciotto
1 and
Simona Scollo
1
1
Istituto Nazionale di Geofisica e Vulcanologia, Osservatorio Etneo—Sezione di Catania, Piazza Roma 2, 95125 Catania, Italy
2
Dipartimento di Scienze Biologiche, Geologiche e Ambientali—Sezione di Scienze della Terra, Università degli Studi di Catania, 95125 Catania, Italy
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(16), 4006; https://doi.org/10.3390/rs14164006
Submission received: 28 June 2022 / Revised: 12 August 2022 / Accepted: 15 August 2022 / Published: 17 August 2022
(This article belongs to the Special Issue Remote Sensing at Istituto Nazionale di Geofisica e Vulcanologia (INGV) — Geophysics and Volcanology Experience)
Browse Figures
Versions Notes

Abstract

:
Between 13 December 2020 and 21 February 2022, Etna volcano produced a sequence of 66 paroxysmal explosive eruptions, with Strombolian activity at the summit craters climaxing in lava fountains and eruption columns extending several kilometers above the craters, accompanied by minor and short-lasting lava flows from the crater rim. We selected three of these episodes that occurred within a short space of time, between 13 December 2020 and 12 March 2021, of different magnitude (i.e., erupted volume) and intensity (i.e., mass eruption rate or instantaneous eruption rate), and analyzed them from a multidisciplinary perspective. The aim was to gain insights into those parameters that mostly reveal the eruptive process for hazard assessment purposes. The multidisciplinary data consist of calibrated visible images, thermal images, seismic and infrasound data, ground deformation detected from the strainmeters, as well as satellite SEVIRI images. From these data, we obtained the timing of each paroxysmal event, the erupted volume in terms of tephra and lava flows, and the corresponding deflation of the source region, together with the development of the lava fountains and eruption columns with time. The results enabled determining that the smallest episode was that of 13 December 2020, which comprised three distinctive pulses but did not produce an eruptive column detectable from either monitoring cameras or satellites. The 28 February 2021 episode was remarkable for the short amount of time required to reach the climax, and was the most intense, whereas the 12 March 2021 event showed the longest duration but with an intensity between that of the previous two. Our results show that these three paroxysmal events display a typical trend, with the first event also being the smallest in terms of both erupted volume and intensity, the second being the most intense, and the third the one of greatest magnitude but less intense than the second. This is coherent with the end of the first paroxysmal phase on 1 April 2021, which was followed by 48 days of eruptive pause before starting again. In this context, the end of the paroxysmal phase was anticipated by a more effusive episode, thus heralding a temporary decline in the gas content within the feeding magma batch.

Graphical Abstract

1. Introduction

Explosive paroxysmal events at Etna volcano have become very frequent over the last few decades, giving rise to eruptive sequences lasting several months [1,2,3,4,5,6,7,8]. Eruptive sequences at Etna are characterized by short-lasting explosive events, with duration of 1–3 h, and occurring every few days or several times a day [3,7]. These episodes have a major impact on the local population, because the ash fallout affects air and ground viability, stability of roofs and buildings, and public health [9,10,11,12,13]. Usually, lava fountain activity at Etna precedes major flank eruptions [14,15,16,17], but this was not so during the most recent paroxysmal explosive sequences [2,3,8]. This unusual behavior allowed Bonaccorso and Calvari [18] to note that the lava fountain sequences are just an alternative way used by the volcano to dissipate the inner energy caused by magma stored at depth from a steady supply. In fact, this energy can be released either through frequent and small-volume lava fountains, or through less frequent and larger-volume effusive eruptions, an occurrence which that has been observed for at least the last five decades [18,19,20,21].
The eruptive activity at Etna volcano is routinely monitored by the Istituto Nazionale di Geofisica e Vulcanologia—Osservatorio Etneo (INGV-OE) through a network of thermal and visible cameras, seismic and infrasonic stations, tiltmeters, GPS (global positioning systems) and strainmeters for the detection of ground deformation, UV scanners for the measurement of SO2 flux from the craters, and by satellites. Predicting the extension of a volcanic plume from initially measured parameters was attempted by Calvari et al. [3]. These authors pointed out the importance of the wind speed on the vertical development of volcanic plumes, with wind speeds greater than 10 m s−1 favoring the formation of weak plumes bending downwind, and vertical to intermediate plumes forming when the wind speed is below this threshold [3]. This assessment is very important for hazard purposes, since a vertical plume has a greater impact on aviation (because it reaches greater elevations) and a lesser effect on the local population (because it remains confined to the summit of the volcano). The opposite applies for weak plumes, which extend further over the flanks of the volcano and less vertically.
The time evolution of the eruptive activity is usually accompanied by variations in both seismic and infrasound signals. In particular, during short-lasting explosive events at Etna, volcanic and infrasonic tremor amplitude increase, together with changes in source locations [7,22,23,24]. Analysis of seismic and infrasound data are routinely performed to monitor and follow the time evolution of volcanic phenomena [1,25], and have proved useful tools to retrieve information on the eruptive dynamics [26,27,28]. In addition, lava fountains are usually accompanied by small deformations of the shallow crust. The analysis of the volumetric strain changes provides useful information towards characterizing the volcano activity both for research purposes and monitoring. The beginning and the ending of the strain variation provide the timing of the onset and of the conclusion of the eruptive event [29]. Moreover, the amplitude of the strain changes reflects the change in volume of the shallow source which empties, fueling the explosive eruption [29,30]. The shallow source propelling the lava fountains is inferred by strain changes at a depth of ~0 km b.s.l. This source is interpreted as a sort of upper valve in which magma is accumulated and then released to generate the lava fountains [29,31]. This interpretation is also in agreement with the recent seismic tomography (January 2020–February 2021) that reveals a smaller upper reservoir at near-sea-level depth [32].
At Etna volcano, lava fountains commonly evolve into eruptive columns and volcanic plumes that expand into the atmosphere for tens of kilometers. The studies on volcanic plumes allow a reliable quantification of the tephra fallout hazard during explosive eruptions [9]. Mainly for this reason, since 2006, the INGV-OE has developed an automatic forecasting system that is able to predict the area that will be covered by tephra fallout [33]. This was recently improved with remote sensing observations of column height estimated by satellite and by visible calibrated cameras in near real time. These observations are available to the on-duty INGV-OE volcanologist during volcanic crises, and allow better constraint of the eruption source parameters in near real time [34].
Satellite remote sensing is moreover currently applied to monitor and quantify the thermal activity associated with volcanic eruptions by processing the middle infrared wavelength bands, a region of the electromagnetic spectrum in which active lava flows and vents emit copious amounts of energy [21]. These bands are available in most weather satellite sensors at high revisit time (from twice a day up to every 5–15 min). As shown by comparisons with thermal camera data, the radiant heat flux signal derived from satellites during lava fountains is mainly produced by the lava flow field expansion and cooling [35] and can be modeled to infer the erupted lava volume [36].
Between 13 December 2020 and 21 February 2022, 66 paroxysmal episodes occurred at the SEC-NSEC crater of Etna volcano involving initial Strombolian activity that, with time, evolved through a transitional stage to lava fountain activity, accompanied by the formation of a sustained eruptive column and volcanic plume, as well as the output of small lava overflows from the crater rim [4,7,8]. From the sequence of 66 episodes at Etna in this span of time, we chose here three events with different magnitude (e.g., erupted volume; [37]) and intensity (e.g., time-averaged discharge rate (TADR), eruption rate (ER), or instantaneous effusion rate (IER) [37,38]). They occurred in a short space of time (December 2020 to March 2021), and we focused on characterizing each of them from a multidisciplinary perspective to identify a possible evolutionary pattern for hazard assessment purposes. To this end, we chose the first and smallest episode on 13–14 December 2020, a middle size event on 12 March 2021, and one of the most powerful events on 28 February 2021. These three episodes occurred during the first eruptive phase, which started in December 2020 and ended in March 2021, followed by a 1.5-month pause [8]. They might display features that recur in each phase. We selected those episodes for which multidisciplinary data were available and of good quality. They are intended to represent a first in-depth multidisciplinary analysis, which needs to be further extended to each episode for a complete comprehension of the whole eruptive process. Below, the three selected episodes are analyzed using multidisciplinary techniques, and their results are compared.

2. Materials and Methods

In this paper, we analyze multidisciplinary data recorded by the monitoring networks of the INGV-OE, the reference institution of the Italian government for the monitoring and hazard assessment of southern Italy volcanoes. The INGV-OE monitoring network comprises several visible and thermal cameras. The cameras used in this paper and their features are listed in Table 1, and their position is shown in Figure 1. The lava fountain height was retrieved from the thermal images recorded by the fixed monitoring cameras as the saturated portion of the image, following the method applied by Calvari et al. [2,3,4]. From the lava fountain height, measured at 1 min time-lapse, multiplied by 60 s and summed up for the whole duration of the episode, we obtained the erupted volume using the formulas:
U = (2gH)0.5
V = U × A × t
where U is the mean fluid exit velocity at the vent, g is the acceleration of gravity, H is the lava fountain height, V is the fluid volume comprising gas and pyroclastics, A is the vent section area, and t is the duration of the lava fountain [2,3,4]. Vent surface area is calculated considering a circular vent with a 30 m diameter [2]. This gives the total erupted volume, comprising gas and pyroclastics. To obtain the pyroclastic volume, we considered 0.18% as the average ratio between the volume of magma and fluids within a typical Etna lava fountain [3], although some deviations from this average value are possible [39].
The eruptive column height above the summit crater (and within 5 km from the volcano summit) was estimated using the method proposed by Scollo et al. [40] and improved by Scollo et al. [34]. It uses two visible cameras (ECV and EBVH, Table 1 and Figure 1b) that were calibrated using the Global Positioning System (GPS) location, the digital elevation model (DEM) of Etna volcano, and assuming that the volcanic plume is within a vertical plane parallel to the wind direction above the volcanic vent. The column height was also obtained using the SEVIRI satellite data, which allows obtaining this value also in a distal position, i.e., beyond the 5 km distance from the craters, provided that enough ash is contained in the plume. We compared the brightness temperature of the most opaque pixel above the vent with the temperature profile downloaded by https://cds.climate.copernicus.eu (accessed on 27 June 2022). This approach has been widely tested and applied to several Etna eruptions [4,41,42].
Thermal satellite remote sensing was used to estimate the radiant heat flux associated with the eruptive activity at Etna. The Meteosat Second-Generation Spinning Enhanced Visible and InfraRed Imager (MSG) SEVIRI acquires data at a sampling time of 15 min, providing the best means to follow from space very fast and short-lived eruptions like the lava fountains occurring in 2020–2021. Infrared satellite data were processed via the HOTSAT system [43,44] in order to locate thermal anomalies, i.e., hotspot pixels, and quantify the thermal activity. The radiant heat flux is mainly produced by the lava flow field expansion, and the cooling portion of the signal is modeled in order to estimate the emplaced lava volume [36].
The INGV-OE seismic and infrasonic stations are equipped with both broadband three-component Nanometrics Trillium 40 s seismometers, with a sampling rate of 100 Hz, and GRASS 40 AN microphones with a flat response with the sensitivity of 50 mV/Pa in the frequency range 0.3–20,000 Hz, with a sampling rate equal to 50 Hz. Volcanic tremor is a continuous signal at Etna, and its temporal evolution was investigated in terms of amplitude and source location. To constrain the location of the volcanic tremor source centroid, a grid search method based on the seismic amplitude decay with distance was applied, assuming propagation in a homogeneous medium [45,46]. In this work, we used a temporal resolution of 5 min. Signals recorded by 16 broadband stations (Figure 1b), located at distances between 1 and 9 km from the center of the summit area were used, and the frequency band 0.5–2.5 Hz was considered. The root mean square (RMS) amplitudes were calculated at the ESLN reference station (Figure 1b) over 81.92-s-long sliding windows, and the signal was filtered between 0.5 and 5 Hz. RMS values falling within 5-min-long time windows were averaged.
The infrasonic signals at Etna are recorded by nine infrasonic stations (Figure 1b), and generally consist of: (i) infrasonic events characterized by duration of less than 1 to more than 30 s, impulsive compression onsets, and peaked spectra with most of the energy in the 0.3–6.0 Hz frequency range [23,47]; (ii) infrasonic tremor, a continuous infrasound signal lasting from minutes to days associated with both paroxysmal activities and degassing processes [27]. Unlike volcanic tremor, the signature of infrasonic events and tremor can be masked by weather-related noise, that is, a broadband, tremor-like signal with variable duration [48]. Thus, the detection of infrasonic events and tremor depends not only on the volcano’s acoustic activity but also on the weather conditions. The infrasonic events were detected by STA/LTA (Short Time Average/Long Time Average) algorithm and located by a grid-search technique based on the brightness function [46,49]. The infrasonic tremor windows were detected and located by cross-correlation-based algorithms (see [46] for further details). In addition, the time series of RMS amplitude at the ESLN station (Figure 1b) was calculated using a 5 min window.
For both seismic and infrasonic signals, a maximum and a cumulative RMS amplitude value were computed for each lava fountain episode at the ESLN station. Furthermore, to quantify the rate of increase of both volcanic tremor and infrasonic amplitude accompanying the waxing phase of the three lava fountains, the slopes of the time series of seismic and infrasonic RMS amplitude were calculated by an approach similar to the one applied by Viccaro et al. [6]. A window was extracted in both the time series (the infrasonic RMS amplitude and the resultant seismic RMS amplitude). In particular, the window ending point was chosen as the time with the highest amplitude value, while the window starting point was the time when the 20% of the maximum amplitude was reached. Then, the slopes of the straight lines joining the starting point and the ending point of the windows were calculated.
Volumetric strain changes are recorded at Etna by Sacks-Evertson strainmeters that warrant the highest resolution (10−11) achievable nowadays using geodetic measurement techniques, with a dynamic range of 140 dB in a frequency range of 10−7 to >20 Hz. Among the four strainmeters operating at Etna [30], the one deployed at Mt Ruvolo (DRUV; Figure 1b) was installed in a massive rock layer with a good efficiency in transferring the strain from the rock to the instrument [29,50]. The strain signal recorded by the borehole strainmeter is usually affected by several disturbing components, mainly due to Earth tides, atmospheric pressure variations, precipitation, and underground water circulation. Such strain components may mask volcano-related strain changes, and hence must be filtered to enhance the capacity to detect volcano deformation [51]. To this end, we used the software BAYTAP-G [52] to filter the disturbing components of the strain signal that persist over the time, namely the tidal and the pressure components, as already applied on Etna [31]. The filtered strain signal is sampled at 5 min. All times in this paper are in UTC format.

3. Results

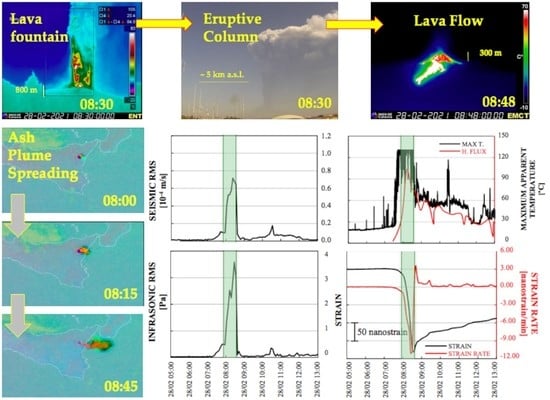
The start and ending time of each episode was obtained from the analysis of the images recorded by the INGV-OE thermal monitoring cameras, together with the erupted volume (pyroclastics), lava fountain height, and proximal volcanic plume height. The volume of erupted lava flows was retrieved from satellites, as well as the distal extension of the volcanic plume. From the above values we have obtained the eruption rates (ER; [38]) distinguishing for the pyroclastics (ERp) and lava flow (ERl) components, divided by the duration of the episode, and the peak instantaneous effusion rate (IER), which is obtained on the pyroclastic portions of the event averaged over 1-min time-lapse. These values are shown in Table 2.

3.1. Volcanology

The three explosive events considered in this paper belong to the phase of paroxysmal explosive activity that started at Etna on 13 December 2020, generating 66 paroxysmal explosive events from the SEC-NSEC, and which had its last episode on 21 February 2022 [8]. The first eruptive episode considered here is also the first of the sequence. It occurred on 13 December 2020 (13D20) late evening (Table 2) after a gradual increase of the Strombolian explosive activity at the summit craters. This episode showed three pulses (13D20, 13–14D20, 14D20) separated by two short-lasting pauses. Visibility was poor at that time because a thick weather cloud was covering the summit of the volcano.
Strombolian activity became visible from the monitoring cameras (EMOT, Table 1) at ~20:17, with billowing hot clouds emerging from the weather cloud and displaying incandescent lava jets at ~20:35. The activity passed to transitional [16] at ~21:30, with almost continuous and low jets of lava from the crater rim. The paroxysmal lava fountaining phase became sustained at 22:00 and lava fountain height increased rapidly, as observed from the ENT monitoring camera (Table 1, Figure 1 and Figure 2a). The lava fountaining phase lasted only 48 min and erupted an estimated volume of pyroclastics of ~0.24 × 106 m3 (Table 2). Pyroclastic density currents (PDCs) formed at 22:15, 22:16 and 22:30 as the result of a sudden collapse of the accumulated spatter on the SW flank of the SEC-NSEC cinder cone, raising a thick dust cloud that hid the visibility of the craters for about 5 min. Two small lava flows emerged from the breached cone at ~22:40, spreading SW and east for a few hundred meters until midnight (Figure 2g).
The eruptive activity at the vent ceased at 22:48, while the lava flow output slowly continued, increasing its speed after also being fed by the fallout of the following explosive pulses. The low height of the lava fountains (maximum 571 m as in Figure 2a, average 231 m, Table 2) and the strong wind enabled the formation of a weak ash plume but no eruptive column [3] (Figure 2a,d). At 23:14 the summit vent again showed mild Strombolian activity that forecasted the start of a new lava fountain pulse at 23:58 [8]. This (13-14D20) ended suddenly at 00:11 on the following day, lasting just 13 min and erupted a volume of pyroclastics estimated at ~0.07 × 106 m3 (Table 2). It had a maximum height of the lava fountains of 400 m, with an average of 235 m (Table 2). The third pulse started at 01:02 on 14 Dec 2020 (14D20) and ended at 01:40 after 38 min, erupting an estimated volume of pyroclastics of ~0.13 × 106 m3, with the lava fountains reaching a maximum height of the lava fountains of 286 m and an average of 121 m (Table 2).
The second paroxysmal explosive episode considered here started on the morning of 28 February 2021 (28F21; Table 2). At 07:03 Strombolian explosive activity was detected from the ENT and EMCT cameras, and rapidly grew to form a sustained lava fountain at ~07:40, when a lava flow also started emerging from the eastern and lower rim of the crater, visible from the EMCT camera, spreading along the steep cone flank towards the Valle del Bove depression (Figure 1b). The height of the lava fountain increased rapidly to ~3600 m (average lava fountain height = 1376 m; Table 2), forming a vertically rising eruption column (strong plume; Figure 2b,e). At 08:24, the lava fountaining phase suddenly ended. The spatter fallout fed by the eruptive column caused two rheomorphic lava flows spreading north and SW. The lava flow spreading east towards the Valle del Bove stopped spreading soon after the end of the paroxysmal explosive phase, at ~08:44. During the emplacement of the strong plume, the wind speed was 9–18 m s−1 at elevations between 5 and 11 km a.s.l.
The third paroxysmal explosive event considered in this paper occurred on 12 March 2021 (12M21), which has already been the object of a dedicated multidisciplinary paper [4]. Strombolian activity began at 02:35 and lava fountain activity lasted from 06:40 to 09:45. It is important to note that powerful and pulsating degassing and intermittent brown ash cloud emissions occurred well before the start of the lava fountain activity from two summit craters of the volcano (Bocca Nuova and Voragine; Figure 1c), located nearby and a few hundred meters away from the erupting SEC-NSEC cone (Figure 1c). Two lava flows emerged from the crater rim at 07:00 and 07:22, spreading east and NE along the upper Valle del Bove (Figure 1b) until 12:00 [4]. The lava fountain had a maximum height of 2400 m and an average value of 1149 m (Table 2). During the emplacement of the intermediate plume, the wind speed was 9–11 m s−1 at elevations between 5 and 10 km a.s.l.
Figure 3 shows the evolution of the eruption column on 28F21 and 12M21. The 13–14 December 2020 eruption column is missing because it was not detected. On 28F21, the column height reached 5.5 km at 07:50 (all the plume heights are estimated a.s.l.) (Figure 3(a1)) and, for 0.5 h and after 08:05 (Figure 3(a2)), it was >9 km. The column height quickly decreased to 6 km after 09:05 (Figure 3(a3)). In this period, considering also the analysis of volcanic plume by SEVIRI satellite images (Figure 3(b1–b3)), we found a maximum plume height of 12.6 km at 08:39 (Table 2) and a mean value of 10.5 km between 08:15 and 08:45. During this event, the column height rapidly grew and then declined within 15 min (Figure 3c). In contrast, the eruption column produced during the 12M21 event was clearly visible between 06:30 and 10:30. At 7:30 the column height was 6.5 km (Figure 3(d1)).
The most intense phase lasted about 1 h, when the volcanic plume was higher than 9 km at 08:30 (Figure 3(d2)) and only after 10:00 (Figure 3(d3)) did it begin to decrease. The maximum height of 10.5 km was estimated at 08:45 using the SEVIRI satellite images (Figure 3(e1–e3)). We also found a mean value of 9.5 km between 08:30 and 09:30. The explosive activity was hence less intense (lower IER) but it lasted for a longer period (Figure 3f), when compared to the 28F21 lava fountain event. The wind speeds from the hydrometeorological service of ARPA in Emilia Romagna [33] are also presented in Table 2, measured at 3.1 and 5.7 and 12 km a.s.l., respectively.
We estimated the slope (or growth rate) of the eruption column variation using the same methodology for the tremor and infrasound and using only the satellite images that were able to retrieve the maximum value of the column height. For 28F21, the slope was 2.7 m s−1 in the time interval between 08:00 and 08:30, whereas, for the 12M21 event, the slope was 1.5 m s−1 on the basis of the images between 08:15 and 08:45.
The SEVIRI-derived radiant heat flux allowed the depiction of the different phases of this activity. The first thermal anomaly was detected on 13 December at 20:40 and was followed by a continuous increase in the radiant heat flux that reached its maximum value of 15.2 GW at 22:45. After this, the thermal activity apparent in the satellite images slowly decreased but resulted in another two peaks of 13.8 GW on 14 December at 00:05 and 12.4 GW at 01:15 associated with the two successive pulses (Figure 4o, red line). By modeling the cooling curve related to these three short events, we were able to compute a cumulative eruptive volume of lava of about 0.79 × 106 m3 (Table 2). The duration of the effusive phase lasted between 22:15 on 13 December and 01:25 on 14 December, for about 190 min, giving an average eruption rate (ERl) of 69.29 m3 s−1 (Table 2). SEVIRI data were also processed in order to compute the plume height and the areal variation of the dispersal. However, during this event we observed a very diluted plume, mostly made up of SO2, thus making it impractical to estimate its height.
The radiant heat flux curve retrieved from SEVIRI images started at 7:30 and was characterized by a sharp increase with the maximum value of about 20 GW reached in less than one hour, at 8:15. After a very short climax, lasting less than 15 min, a slow decrease, typical of lava cooling, was observed (Figure 4p, red line). In this case, the volume from cooling was estimated at 1.45 × 106 m3. Considering that the effusive phase lasted from 07:40 to 08:44, for about 64 min, it gave an average eruption rate (ERl) of 377.60 m3 s−1 (Table 2). Meanwhile, the maximum value for the ash top height from satellite was observed at 8:30 and resulted in about 12.6 km a.s.l. (Figure 3). The impulsive nature of this event is also quantifiable from the plume area expansion, which reached its maximum value in about 1.5 h, with a velocity of about 0.4 km2 s−1 (Figure 4j, red line).
The SEVIRI-derived radiant heat flux recorded the first thermal anomaly on 12 March at 03:00 with an initially slow increase, which became faster at 06:45 and steep from 08:15 (Figure 4q, red line). The maximum value of about 25 GW was observed at 09:00 and the modeling of the successive cooling curve allowed estimating a volume of 2.4 × 106 m3 for the lava flow field that was emplaced from 06:54 to 12:00 resulting in an average eruption rate (ERl) of 130.72 m3 s−1 (Table 2).
SEVIRI data were also processed in order to compute the plume height and the areal variation of the dispersal. The maximum plume height above the volcano summit was about 10.4 km (Figure 3f). It is worth noting that this volcanic cloud reached its highest elevation, up to 12 km, spreading to the southeast about 100 km far from the volcano summit. The expansion of the plume area reached its maximum value in about 2.5 h, with a velocity of about 0.2 km2 s−1 (Figure 4k, red line).

3.2. Seismicity and Infrasound

Paroxysmal explosive episodes were also investigated by means of volcanic tremor and infrasound signal analysis. To follow the eruptive dynamics, the following parameters were retrieved: (i) seismic RMS amplitude (Figure 4a–c); (ii) infrasound RMS amplitude (Figure 4d–f); (iii) volcanic tremor source centroids (Figure 5a–f and Figure 6); (iv) infrasound event amplitudes and source locations (Figure 5g–j and Figure 6), and (v) infrasound tremor amplitudes and source locations (Figure 5k–n and Figure 6). The network configuration was not dense enough to allow good quality estimation of volcanic tremor and infrasound signal source location for the 13D20, 13–14D20, and 14D20 pulses.
All the considered lava fountain episodes show amplitude increases in both the seismic and infrasonic signals during the waxing phases; the highest amplitude values were reached during the lava fountaining phase, and amplitude decreasing trends were observed during the waning phases. In addition, seismic and infrasonic amplitude time evolution (Figure 4a–f) allowed the identification of differences among paroxysmal episodes, which confirm volcanological observations. In particular, the fountain showing the highest values of maximum and cumulative seismic RMS amplitude was the 12M21, while the fountains with the lowest values of maximum and cumulative amplitudes were the 13D20 and the 28F21, respectively (Table 3). Regarding infrasound, the fountains with the highest values of maximum and cumulative amplitudes were the 28F21 and the 12M21, respectively, and the fountains with the lowest values of maximum and cumulative amplitudes were the 13D20 and the 28F21, respectively (Table 3). Concerning the temporal trend of the elastic radiation, for the 13D20 and 12M21 episodes, the patterns of amplitude increase, for both seismic and infrasound data, were gradual, although it was longer for the 12M21 episode. The phase of amplitude increase was instead very rapid for the 28F21 episode (Figure 4a–f). These different behaviors are reflected in the slope values, computed in the time series of both seismic and infrasonic amplitudes, which show the highest values for the 28F21 episode (Table 3).
Source locations of volcanic tremor had the same pattern for both the 28F21 and the 12M21 episodes. Source centroids migrated from the BN crater area towards the SEC-NSEC area a few tens of minutes before the beginning of the seismic amplitude increase (Figure 5a–d and Figure 6), becoming simultaneously shallower (Figure 5e,f and Figure 6), and then went back at the end of the episode. With regard to the infrasound signal, background activity during February to March 2021 consisted of low-amplitude discrete transients, and sometimes tremor, located at BN and NEC craters (Figure 5g–n and Figure 6a,b). During the paroxysmal episodes, infrasound sources in the SEC-NSEC area were also recorded. In particular, the first signals to be recorded and located were discrete transients (Figure 5k–n and Figure 6a,b), which later on merged into a continuous infrasound tremor (Figure 5k–n). Furthermore, the eruptive episode of 12M21 was characterized by a higher number of infrasound events and tremor windows, due to the longer duration of both strombolian and sustained lava fountain phases.

3.3. Strain

The strain signal provides significant information for characterizing the lava fountain events. During the eruptive episodes, the filtered strain signal showed negative strain variations that correspond to dilatation of the rock surrounding the DRUV sensor. These variations are attributable to the decompression of the shallow magma reservoir, which supplied magma to the lava fountain. The beginning and the ending of such variations mark the onset and the end of each eruptive episode precisely, which match those obtained from thermal cameras. The amplitude of the strain variations and the strain rate signal (Figure 4g) are indicative of the amount of magma withdrawal and its speed [29,31]. The decompression rate is estimated by computing the linear slope of the strain signal during the eruptive events (Table 3). The 13D20 lava fountain was the smallest eruptive episode among those analyzed in terms of the amplitude of the strain rate variations (Figure 4g). Three distinct strain transients can be observed concurrently with the three pulses that characterized this small eruptive event. The strain variation related to the first pulse, which is also the longest-lasting among the three pulses, is the largest in terms of both amplitude and average strain rate (Table 3), exhibiting values of 76.1 nanostrain and −1.4 nanostrain/min, respectively. The other two pulses showed progressively lower values of both amplitude and average strain rate of 12.2 and 7.7 nanostrain and −1.0 and −0.2 nanostrain/min, respectively. The 28F21 lava fountain was the most intense in terms of strain rate (Figure 4h). The value of the strain decreased abruptly during the lava fountain with an average strain rate of −3.8 nanostrain/min. This eruptive event was also the one that exhibited the largest deformation, with a value of 228.5 nanostrain. The 12M21 lava fountain was less intense than that of the 28F21 episode (Figure 4i), showing a value of the average strain rate of −1.3 nanostrain/min. However, this lava fountain was the event with the longest duration, and its cumulative dilatation is larger than that related to the 13D20 event, but smaller than that of the 28F21 episode, showing a value of 169.5 nanostrain.

4. Discussion

Considering the images of the monitoring cameras related to the three selected events reported in Figure 2, their different size, in terms of height of the lava fountains, volcanic plume, erupted volume, ER and IER (Table 2) appear clear. It is worth noting here that the value of IER refers only to the pyroclastic portion of each event, whereas the ER has been distinguished as ERp for pyroclastic and ERl for lava flows. The peak IER of 338 m3 s−1 for the 28F21 episode was recorded just a few minutes before the end of the lava fountain phase (Table 2), showing the extremely impulsive and high intensity of this event. The highest values of ER, i.e., 216.05 m3 s−1 for pyroclastic and 377.60 m3 s−1 for lava flows, were instead determined by the short duration of the episode (just 54 min, Table 2), given that the total erupted volume was about half that of the 12M21 event. The first lava fountain episode comprised three discrete pulses (13D20, 13–14D20, 14D20), and had an average lava fountain height of 121–235 m above the vent (Table 2). This episode was so small that no eruptive column developed (Figure 2a,d), and no volcanic plume could be detected from the satellite during the three pulses. Applying the formula proposed by Calvari et al. [3] to the average lava fountain height to obtain the maximum plume height, we obtain for the three pulses ~8 km a.s.l. as the maximum vertical extension of the volcanic plume. However, it is possible that because the eruption occurred during the night, it might have obscured the visibility of the volcanic plume to the cameras. Additionally, the lava flow erupted from the crater rim during the entire episode was very small, and barely visible from the monitoring camera (Figure 2g). The lava flow volume of 0.79 × 106 m3 retrieved via satellite refers to the cumulate erupted during the three pulses (13D20, 13-14D20, 14D20; Table 2) comprising this episode. This was the smallest episode of the three considered here, and also the one with the smallest lava flow field (Table 2 and Figure 2g), followed by the lava flow field of the 28F21 episode of intermediate size (1.45 × 106 m3, Table 2 and Figure 2h), whereas the lava flow field of the 12M21 episode was the widest (2.40 × 106 m3; Table 2 and Figure 2i). Conversely, it appears very clear from the extension of the lava fountains and eruptive plumes (Figure 2a–f and Figure 3) that the first episode (13D20, 13–14D20, 14D20) was the smallest in terms of magnitude and erupted volume (Table 2) and in terms of intensity (IER = 85–135 m3 s−1, ERp = 57.02–89.74 m3 s−1 and ERl = 69.29 m3 s−1); the second 28F21 was the most intense (IER = 388 m3 s−1 and ERp of 216.05 m3 s−1), with an expansion velocity of the ash plume area of about 0.4 km2 s−1; and the third 12M21 was the one with the greatest magnitude (1.63 × 106 m3 for pyroclastics and 2.40 × 106 m3 for lava flows). By summing up the volume of pyroclastics and lava flows, the total volumes would be 1.23 × 106 m3 for the first, 2.15 × 106 m3 for the second and 4.03 × 106 m3 for the third episode, thus implying average eruption rates of 207.1 m3 s−1, 663.6 m3 s−1 and 363.1 m3 s−1, respectively. However, when dealing with the total erupted volume of paroxysmal eruptions at Etna, it is necessary to consider that a certain amount of the erupted pyroclastics might be removed and flow downslope to feed the lava flows, as recently observed for the 12M21 episode [4]. It is then likely that the total erupted volume is less than just summing up the volume of pyroclastics and the volume of lava flows, because an overlap of the two of ~30% was observed [4]. The lava fountain heights reflect the size of the eruptive columns, with the tallest lava fountains (28F21, on average 1376 m; Figure 2b,e and Table 2) being associated with the highest eruptive plumes (12.6 km; Table 2 and Figure 3).
The peaks in lava fountain heights and eruptive columns are associated with the highest value of maximum infrasonic RMS amplitude and with the largest recorded strain and strain rate, thus suggesting that these parameters are strictly correlated (Figure 4 and Table 3). This is not so for the seismic radiation showing the highest value of maximum RMS amplitude during the 12M21 episode (Figure 4 and Table 3).
Strain signal gives a strong indication of the decompression of the magma chamber that feeds the eruptive events. During the lava fountains the strain variation is caused by the volume contraction (ΔVs) of the source, which empties itself feeding the lava fountain. The position of the source, representing a sort of upper valve, is stable over time as inferred by the strain signals [29], and as also confirmed by seismic tomography [32]. The ΔVs and, therefore, the recorded strain change are proportional to the total erupted volume, which comprises both explosive (pyroclastics and gas) and effusive (lava flow) portions [29,30,31]. Depending on the gas content, the lava fountains can show different degree of explosive intensity. In conditions of gas-rich magma with more predominant portion of pyroclastics and gas, high values of ΔVs can be reached as well, generating more explosive events with associated greater columns, as in the 28F21 case, and smaller portion of effusive lava flows than in the 12M21 case. Table 3 shows that the decompression rates, computed in terms of strain slope and maximum strain rate, correlate well with the height of the lava fountain and the duration of the event (Table 2). The highest value of the strain rate signal is observed in correspondence with the fasTest 28F21 episode (Table 3). The other parameters reported in Table 3 also exhibit larger slope values during the 28F21 event. These findings are in agreement with the results reported in [53] showing that the amplitude and the rate of geodetic signals and the seismic and infrasonic eruption tremors can be considered as a proxy of the magma ascent rate and, hence, of the lava fountain height.
The lower part of Figure 3 shows the radiant heat flux detected from satellite images and the maximum temperature recorded by the ENT thermal monitoring camera, which show a good agreement between them and with the seismic RMS. In fact, these signals display the greater values for the 12M21 third episode, whereas for the second 28F21 event they display intermediate values. We suggest that the radiant heat flux, the maximum temperature, and the seismic RMS amplitude are sensitive to the size and the extent of the lava flow field and/or to the lava flow emission, thus showing greater values when a larger volume of lava is erupted from the vent. This means that these parameters reflect the magnitude (or erupted volume) of a paroxysmal event. Conversely, the infrasonic RMS, the strain, and the maximum height of the lava fountain and maximum height of the eruptive column, are all related to the IER, thus reflecting the intensity of a paroxysmal event. We propose that paroxysmal events displaying higher intensity might be related to higher decompression rates and faster magma ascent. This is supported by experimental results from [54] based on melt inclusions and olivine compositions, suggesting that higher decompression rates are correlated with faster magma ascent and more explosive eruptions, with the difference that our results, being based on a multidisciplinary monitoring system, are able to gather this information in real time.
From the plume height values, we also estimated the maximum mass eruption rate (MER) of the pyroclastic portion building up the volcanic plume using the formula of Mastin et al. [55]. The maximum value of MER was 1.5 × 106 and 4.8 × 105 kg s−1 for the 28F21 and 12M21, respectively. Consequently, 28F21 was more intense than 12M21 and comparable with the higher-MER lava fountains that occurred in the past (e.g., the 24 September 1986, 5 January 1990 and 22 July 1998 lava fountains; see [56]). Mainly for this reason, 28F21 was also similar to the strong plume scenario that is run daily at INGV-OE in the automatic volcanic ash forecasting system [33]. In fact, those events produced a copious tephra fallout on Etna volcano flanks, seriously impacting the aviation operations, road transport and causing damage to crops and vegetation [9].
It is worth noting that the strong plume that formed during the 28F21 episode emplaced in conditions of wind blowing at a higher speed than for the episode of 12M21, which had a lower elevation of the plume (see Table 2). This was likely caused by the high values of both ER and IER (Table 2) for the 28F21 episode, which pushed the pyroclastics into the atmosphere, forming a strong plume even when the wind conditions were more favorable to the development of an intermediate or weak plume [3].
As observed during the lava fountain episodes at Mt. Etna [6,46,57], during both the 28F21 and the 12M21 episodes, the centroids of the volcanic tremor source migrated from the BN/VOR area toward the SEC-NSEC area at shallower depths (Figure 5a–f and Figure 6). The different pattern of the depth of the volcanic tremor centroid during the 28F21 and 12M21 fountains could be due to either the involvement of a deeper tremor source during the former episode, pulling the tremor centroid deeper, or to the more energetic shallow tremor sources during the latter episode, hiding the possible contribution of deeper tremor sources. Since the amplitude of volcanic tremor preceding and following the 28F21 fountain was lower than the amplitude of volcanic tremor preceding and following the 12M21 fountain, the second explanation seems more plausible. Regarding the infrasound, in both the 28F21 and 12M21 episodes, three acoustic sources were observed: BN, NEC and SEC-NSEC (Figure 5g–n and Figure 6). It is worth noting that the first two are associated with degassing activity, while the third one is associated with explosive activity.

5. Conclusions

We estimated the column height above the Etna summit craters and its time-variation for the 28F21 and 12M21 events using both the visible calibrated camera and satellite images. Data showed that the 13D20, 13-14D20 and 14D20 pulses did not develop a detectable volcanic plume, and that the 28F21 episode produced a higher eruption column than the 12M21 event. However, the 28F21 eruption column reached heights greater than 9 km for only 40 min, whereas the 12M21 event lasted for more than 3 h. Consequently, the pyroclastic volume of the 28F21 event was lower than the 12M21 event.
The three paroxysmal events considered here, although representing a small sample of an eruptive sequence that comprised 66 eruptive episodes, display a typical trend, with the first event also being the smallest in terms of both magnitude and erupted volume (1.23 × 106 m3, considering both pyroclastics and lava flows) and intensity (IER = 85–135 m3 s−1, ERp = 57.02–89.74 m3 s−1 and ERl = 69.29 m3 s−1), the second 28F21 episode being the most intense (IER = 338 m3 s−1, ERp = 216.04 m3 s−1 and ERl = 377.60 m3 s−1), and the third 12M21 episode the one with the greatest magnitude (Volume of lava flows = 2.40 × 106 m3 and volume of pyroclastics = 1.63 × 106 m3; Table 2), but less intense than 28F21 (IER = 276 m3 s−1, ERp = 146.85 m3 s−1 and ERl = 130.72 m3 s−1). This is coherent with the end of the first paroxysmal phase, occurring on 1 April 2021, which was followed by 48 days of eruptive pause before starting again [8]. In this context, the end of the paroxysmal phase was anticipated by a more effusive episode (12M21), thus suggesting a temporary decline of the gas content within the feeding magma batch.
Even though we take into consideration only three episodes, the results show that seismic and infrasound signals, in terms of maximum amplitude, could represent a proxy of magnitude, in the case of the former, and of the intensity of the paroxysm, in the case of the latter. Furthermore, the slopes of the amplitude time series of both the seismic and infrasonic signals are higher for the 28F21 episode, thus suggesting that this parameter could reflect the impulsivity and the intensity of the paroxysm.

Author Contributions

Conceptualization, S.C.; methodology, S.C., E.B., A.B., A.C., L.C., G.C., G.D.G., G.G., A.I., E.P., M.P., M.S. and S.S.; software, M.P. and E.P.; validation, S.C., A.B., A.C., G.C., G.D.G., G.G., M.S. and S.S.; formal analysis, S.C., E.B., A.B., A.C., L.C., G.C., G.D.G., G.G., A.I., E.P., M.P., M.S. and S.S.; investigation, S.C., A.B., A.C., G.C., G.D.G., G.G., M.S. and S.S.; resources, S.C.; data curation, S.C., M.P., S.S., E.P., L.C., M.S. and A.C.; writing—original draft preparation, S.C.; writing—review and editing, S.C., A.B., A.C., G.G., M.S. and S.S.; visualization, S.C., M.P. and L.C.; supervision, S.C.; project administration, S.C.; funding acquisition, S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Project FIRST-ForecastIng eRuptive activity at Stromboli volcano: Timing, eruptive style, size, intensity, and duration; INGV-Progetto Strategico Dipartimento Vulcani 2019 (Delibera n. 144/2020). A.C. thanks the CHANCE project, II Edition, Università degli Studi di Catania (principal investigator A.C.) and the grant PIACERI, 2020-22 programme (PAROSSISMA project, code 22722132140; principal investigator Marco Viccaro). A.I. thanks the IMPACT project—A Multidisciplinary Insight on the Kinematics and Dynamics of Magmatic Processes at Mt. Etna Aimed at Identifying Rrecursor Phenomena and Developing Early Warning Systems, funded by INGV-Progetto Strategico Dipartimento Vulcani 2019 (Delibera n. 144/2020). S.S. thanks the ‘e-shape’ project, which receives funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement 820852. L.C. is supported by EC H2020-FET OPEN project “SiC optical nano-strain-meters for pico-detection in Geosciences” (acronym SiC nano for picoGeo) grant agreement n. 863220.

Data Availability Statement

The data used in this paper belong to INGV and can be made available upon request to the authors.

Acknowledgments

We would like to thank the INGV-OE scientists and technicians for the monitoring network maintenance.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Alparone, S.; Andronico, D.; Sgroi, T.; Ferrari, F.; Lodato, L.; Reitano, D. Alert system to mitigate tephra fallout hazards at Mt. Etna Volcano, Italy. Nat. Hazards 2007, 43, 333–350. [Google Scholar] [CrossRef]
  2. Calvari, S.; Salerno, G.G.; Spampinato, L.; Gouhier, M.; La Spina, A.; Pecora, E.; Harris, A.J.L.; Labazuy, P.; Biale, E.; Boschi, E. An unloading foam model to constrain Etna’s 11–13 January 2011 lava fountaining episode. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
  3. Calvari, S.; Cannavò, F.; Bonaccorso, A.; Spampinato, L.; Pellegrino, A.G. Paroxysmal Explosions, Lava Fountains and Ash Plumes at Etna Volcano: Eruptive Processes and Hazard Implications. Front. Earth Sci. 2018, 6, 107. [Google Scholar] [CrossRef]
  4. Calvari, S.; Bonaccorso, A.; Ganci, G. Anatomy of a Paroxysmal Lava Fountain at Etna Volcano: The Case of the 12 March 2021, Episode. Remote Sens. 2021, 13, 3052. [Google Scholar] [CrossRef]
  5. Andronico, D.; Corsaro, R.A. Lava fountains during the episodic eruption of South–East Crater (Mt. Etna), 2000: Insights into magma-gas dynamics within the shallow volcano plumbing system. Bull. Volcanol. 2011, 73, 1165–1178. [Google Scholar] [CrossRef]
  6. Viccaro, M.; Garozzo, I.; Cannata, A.; Di Grazia, G.; Gresta, S. Gas burst vs. gas-rich magma recharge: A multidisciplinary study to reveal factors controlling triggering of the recent paroxysmal eruptions at Mt. Etna. J. Volc. Geoth. Res. 2014, 278–279, 1–13. [Google Scholar] [CrossRef]
  7. Andronico, D.; Cannata, A.; Di Grazia, G.; Ferrari, F. The 1986–2021 paroxysmal episodes at the summit craters of Mt. Etna: Insights into volcano dynamics and hazard. Earth-Sci. Rev. 2021, 220, 103686. [Google Scholar] [CrossRef]
  8. Calvari, S.; Nunnari, G. Comparison between Automated and Manual Detection of Lava Fountains from Fixed Monitoring Thermal Cameras at Etna Volcano, Italy. Remote Sens. 2022, 14, 2392. [Google Scholar] [CrossRef]
  9. Scollo, S.; Coltelli, M.; Bonadonna, C.; Del Carlo, P. Tephra hazard assessment at Mt. Etna (Italy). Nat. Hazards Earth Syst. Sci. 2013, 13, 1–13. [Google Scholar] [CrossRef]
  10. Andronico, D.; Del Carlo, P. PM10 measurements in urban settlements after lava fountain episodes at Mt. Etna, Italy: Pilot test to assess volcanic ash hazard to human health. Nat. Hazards Earth Syst. Sci. 2016, 16, 29–40. Available online: www.nat-hazards-earth-syst-sci.net/16/29/2016/ (accessed on 1 January 2022).
  11. Horwell, C.J.; Sargent, P.; Andronico, D.; Lo Castro, M.D.; Tomatis, M.; Hillman, S.E.; Michnowicz, S.A.K.; Fubini, B. The iron-catalysed surface reactivity and health-pertinent physical characteristics of explosive volcanic ash from Mt. Etna, Italy. J. Appl. Volcanol. 2017, 6, 12. [Google Scholar] [CrossRef]
  12. Pavolonis, M.J.; Sieglaff, J.; Cintineo, J. Automated detection of explosive volcanic eruptions using satellite-derived cloud vertical growth rates. Earth Space Sci. 2018, 5, 903–928. [Google Scholar] [CrossRef]
  13. Paredes-Mariño, J.; Forte, P.; Alois, S.; Chan, K.L.; Cigala, V.; Mueller, S.B.; Poret, M.; Spanu, A.; Tomasšek, I.; Tournigan, P.-Y.; et al. The lifecycle of volcanic ash: Advances and ongoing challenges. Bull. Volcanol. 2022, 84, 51. [Google Scholar] [CrossRef]
  14. Andronico, D.; Branca, S.; Calvari, S.; Burton, M.R.; Caltabiano, T.; Corsaro, R.A.; Del Carlo, P.; Garfì, G.; Lodato, L.; Miraglia, L.; et al. A multi-disciplinary study of the 2002–03 Etna eruption: Insights for a complex plumbing system. Bull. Volc. 2005, 67, 314–330. [Google Scholar] [CrossRef]
  15. Branca, S.; Del Carlo, P. Types of eruptions of Etna volcano AD 1670-2003: Implications for short-term eruptive behaviour. Bull. Volcanol. 2005, 67, 732–742. [Google Scholar] [CrossRef]
  16. Spampinato, L.; Calvari, S.; Oppenheimer, C.; Lodato, L. Shallow magma transport for the 2002–2003 Mt. Etna eruption inferred from thermal infrared surveys. J. Volcanol. Geotherm. Res. 2008, 177, 301–312. [Google Scholar] [CrossRef]
  17. Bonaccorso, A.; Bonforte, A.; Calvari, S.; Del Negro, C.; Di Grazia, G.; Ganci, G.; Neri, M.; Vicari, A.; Boschi, E. The initial phases of the 2008–2009 Mt. Etna eruption: A multi-disciplinary approach for hazard assessment. J. Geophys. Res. 2011, 116, B03203. [Google Scholar] [CrossRef]
  18. Bonaccorso, A.; Calvari, S. Major effusive eruptions and recent lava fountains: Balance between erupted and expected magma volumes at Etna volcano. Geophys. Res. Lett. 2013, 40, 6069–6073. [Google Scholar] [CrossRef]
  19. Wadge, G.; Walker, G.P.L.; Guest, J.E. The output of the Etna volcano. Nature 1975, 255, 385–387. [Google Scholar] [CrossRef]
  20. Wadge, G.; Guest, J.E. Steady-state magma discharge at Etna 1971–1981. Nature 1981, 294, 548–550. [Google Scholar] [CrossRef]
  21. Harris, A.J.L.; Steffke, A.; Calvari, S.; Spampinato, L. Thirty years of satellite-derived lava discharge rates at Etna: Implications for steady volumetric output. J. Geophys. Res. 2011, 116, B08204, Erratum in J. Geophys. Res. 2012, 117, B08207. [Google Scholar] [CrossRef]
  22. Alparone, S.; Andronico, D.; Lodato, L.; Sgroi, T. Relationship between tremor and volcanic activity during the Southeast Crater eruption on Mount Etna in early 2000. J. Geophys. Res. 2003, 108, 2241. [Google Scholar] [CrossRef]
  23. Cannata, A.; Montalto, P.; Privitera, E.; Russo, G.; Gresta, S. Tracking eruptive phenomena by infrasound: 13 May 2008 eruption at Mt. Etna. Geophys. Res. Lett. 2009, 36, 5. [Google Scholar] [CrossRef]
  24. Spampinato, L.; Sciotto, M.; Cannata, A.; Cannavò, F.; La Spina, A.; Palano, M.; Salerno, G.G.; Privitera, E.; Caltabiano, T. Multiparametric study of the February–April 2013 paroxysmal phase of Mt. Etna New South-East crater. Geochem. Geophys. Geosyst. 2015, 16, 1932–1949. [Google Scholar] [CrossRef]
  25. D’Agostino, M.; Di Grazia, G.; Ferrari, F.; Langer, H.; Messina, A.; Reitano, D.; Spampinato, S. Volcano Monitoring and Early Warning on Mt Etna Based on Volcanic Tremor—Methods and Technical Aspects; Nova Science Publishers: New York, NY, USA, 2013; Volume 4, pp. 53–92. [Google Scholar]
  26. Patanè, D.; Di Grazia, G.; Cannata, A.; Montalto, P.; Boschi, E. Shallow magma pathway geometry at Mt. Etna volcano. Geochem. Geophys. Geosyst. 2008, 9, Q12021. [Google Scholar] [CrossRef]
  27. Cannavò, F.; Sciotto, M.; Cannata, A.; Di Grazia, G. An integrated geophysical approach to track magma intrusion: The 2018 Christmas eve eruption at Mt. Etna. Geophys. Res. Lett. 2019, 46, 8009–8017. [Google Scholar] [CrossRef]
  28. Sciotto, M.; Cannata, A.; Prestifilippo, M.; Scollo, S.; Fee, D.; Privitera, E. Unravelling the links between seismo-acoustic signals and eruptive parameters: Etna lava fountain case study. Sci. Rep. 2019, 9, 16417. [Google Scholar] [CrossRef]
  29. Bonaccorso, A.; Currenti, G.; Linde, A.T.; Sacks, S. New data from borehole strainmeters to infer lava fountain sources (Etna 2011–2012). Geophys. Res. Lett. 2013, 40, 3579–3584. [Google Scholar] [CrossRef]
  30. Bonaccorso, A.; Linde, A.T.; Currenti, G.; Sacks, S.; Sicali, A. The borehole dilatometer network of Mount Etna: A powerful tool to detect and infer volcano dynamics. J. Geophys. Res. 2016, 121, 4655–4669. [Google Scholar] [CrossRef]
  31. Bonaccorso, A.; Carleo, L.; Currenti, G.; Sicali, A. Magma Migration at Shallower Levels and Lava Fountains Sequence as Revealed by Borehole Dilatometers on Etna Volcano. Front. Earth Sci. 2021, 9, 740505. [Google Scholar] [CrossRef]
  32. De Gori, P.; Giampiccolo, E.; Cocina, O.; Branca, S.; Doglioni, C.; Chiarabba, C. How Long Re-pressurized Magma Can Feed Eruptions at Mt. Etna. Commun. Earth Environ. 2021, 2, 216. [Google Scholar] [CrossRef]
  33. Scollo, S.; Prestifilippo, M.; Spata, G.; D’Agostino, M.; Coltelli, M. Monitoring and forecasting Etna volcanic plumes. Nat. Hazards Earth Syst. Sci. 2009, 9, 1573–1585. [Google Scholar] [CrossRef]
  34. Scollo, S.; Prestifilippo, M.; Bonadonna, C.; Cioni, R.; Corradini, S.; Degruyter, W.; Rossi, E.; Silvestri, M.; Biale, E.; Carparelli, G.; et al. Near-real-time tephra fallout assessment at Mt. Etna, Italy. Remote Sens. 2019, 11, 2987. [Google Scholar] [CrossRef]
  35. Ganci, G.; James, M.R.; Calvari, S.; Del Negro, C. Separating the thermal fingerprints of lava flows and simultaneous lava fountaining using ground-based thermal camera and SEVIRI measurements. Geophys. Res. Lett. 2013, 40, 5058–5063. [Google Scholar] [CrossRef]
  36. Ganci, G.; Harris, A.J.L.; Del Negro, C.; Guéhenneux, Y.; Cappello, A.; Labazuy, P.; Calvari, S.; Gouhier, M. A year of lava fountaining at Etna: Volumes from SEVIRI. Geophys. Res. Lett. 2012, 39, L06305. [Google Scholar] [CrossRef]
  37. Walker, G.P.L. Explosive volcanic eruptions—A new classification scheme. Geol. Rundsch. 1973, 62, 431–446. [Google Scholar] [CrossRef]
  38. Harris, A.J.L.; Dehn, J.; Calvari, S. Lava effusion rate definition and measurement: A review. Bull. Volcanol. 2007, 70, 1–22. [Google Scholar] [CrossRef]
  39. Bonaccorso, A.; Calvari, S. A new approach to investigate an eruptive paroxysmal sequence using camera and strainmeter networks: Lessons from the 3–5 December 2015 activity at Etna volcano. Earth Plan. Sci. Lett. 2017, 475, 231–241. [Google Scholar] [CrossRef]
  40. Scollo, S.; Prestifilippo, M.; Pecora, E.; Corradini, S.; Merucci, L.; Spata, G.; Coltelli, M. Eruption column height estimation of the 2011–2013 Etna lava fountains. Ann. Geophys. 2014, 57, S0214-61. [Google Scholar]
  41. Corradini, S.; Montopoli, M.; Guerrieri, L.; Ricci, M.; Scollo, S.; Merucci, L.; Marzano, F.; Pugnaghi, S.; Prestifilippo, M.; Ventress, L.; et al. A Multi-Sensor Approach for Volcanic Ash Cloud Retrieval and Eruption Characterization: The 23 November 2013 Etna Lava Fountain. Remote Sens. 2016, 8, 58. [Google Scholar] [CrossRef]
  42. Corradini, S.; Guerrieri, L.; Lombardo, V.; Merucci, L.; Musacchio, M.; Prestifilippo, M.; Scollo, S.; Silvestri, M.; Spata, G.; Stelitano, D. Proximal Monitoring of the 2011–2015 Etna Lava Fountains Using MSG-SEVIRI Data. Geosciences 2018, 8, 140. [Google Scholar] [CrossRef]
  43. Ganci, G.; Vicari, A.; Fortuna, L.; Del Negro, C. The HOTSAT volcano monitoring system based on a combined use of SEVIRI and MODIS multispectral data. Ann. Geophys. 2011, 54, 5. [Google Scholar] [CrossRef]
  44. Ganci, G.; Bilotta, G.; Cappello, A.; Hérault, A.; Del Negro, C. HOTSAT: A multi-platform system for the satellite thermal monitoring of volcanic activity. Geol. Soc. Lond. Spec. Publ. 2016, 426, 207–221. [Google Scholar] [CrossRef]
  45. Di Grazia, G.; Falsaperla, S.; Langer, H. Volcanic tremor location during the 2004 Mount Etna lava effusion. Geophys. Res. Lett. 2006, 33, 4. [Google Scholar] [CrossRef]
  46. Cannata, A.; Di Grazia, G.; Aliotta, M.; Cassisi, C.; Montalto, P.; Patanè, D. Monitoring seismo-volcanic and infrasonic signals at volcanoes: Mt. Etna case study. Pure Appl. Geophys. 2013, 170, 1751–1771. [Google Scholar] [CrossRef]
  47. Cannata, A.; Montalto, P.; Privitera, E.; Russo, G. Characterization and location of infrasonic sources in active volcanoes: Mount Etna, September–November 2007. J. Geophys. Res. 2009, 114, B8. [Google Scholar] [CrossRef]
  48. Johnson, J.B.; Aster, R.C.; Ruiz, M.C.; Malone, S.D.; McChesney, P.J.; Lees, J.M.; Kyle, P.R. Interpretation and utility of infrasonic records from erupting volcanoes. J. Volcanol. Geoth. Res. 2003, 121, 15–63. [Google Scholar] [CrossRef]
  49. Cannata, A.; Sciotto, M.; Spampinato, L.; Spina, L. Insights into explosive activity at closely-spaced eruptive vents using infrasound signals: Example of Mt. Etna 2008 eruption. J. Volcanol. Geoth. Res. 2011, 208, 1–11. [Google Scholar] [CrossRef]
  50. Currenti, G.; Zuccarello, L.; Bonaccorso, A.; Sicali, A. Borehole Volumetric Strainmeter Calibration From a Nearby Seismic Broadband Array at Etna Volcano. J. Geophys. Res. 2017, 112, 7729–7738. [Google Scholar] [CrossRef]
  51. Currenti, G.; Bonaccorso, A. Cyclic magma recharge pulses detected by high-precision strainmeter data: The case of 2017 inter-eruptive activity at Etna volcano. Sci. Rep. 2019, 9, 7553. [Google Scholar] [CrossRef]
  52. Tamura, Y.; Sato, T.; Ooe, M.; Ishiguro, M. A procedure for tidal analysis with a Bayesian information criterion. Geophys. J. Int. 1991, 104, 507–516. [Google Scholar] [CrossRef]
  53. Ichihara, M. Seismic and infrasonic eruption tremors and their relation to magma discharge rate: A case study for sub-Plinian events in the 2011 eruption of Shinmoe-dake, Japan. J. Geophys. Res. 2016, 121, 7101–7118. [Google Scholar] [CrossRef]
  54. Barth, A.; Newcombe, M.; Plank, T.; Gonnermann, H.; Hajimirza, S.; Soto, G.J.; Saballos, A.; Hauri, E. Magma decompression rate correlates with explosivity at basaltic volcanoes—Constraints from water diffusion in olivine. J. Volcanol. Geoth. Res. 2019, 387, 106664. [Google Scholar] [CrossRef]
  55. Mastin, L.G.; Guffanti, M.; Servranckx, R.; Webley, P.; Barsotti, S.; Dean, K.; Durant, A.; Ewert, J.W.; Neri, A.; Rose, W.I.; et al. A multidisciplinary effort to assign realistic source parameters to models of volcanic ash-cloud transport and dispersion during eruptions (Book review). J. Volcanol. Geotherm. Res. 2009, 186, 10–21. [Google Scholar] [CrossRef]
  56. Andronico, D.; Scollo, S.; Cristaldi, A. Unexpected hazards from tephra fallouts at Mt Etna: The 23 November 2013 lava fountain. J. Volcanol. Geotherm. Res. 2015, 304, 118–125. [Google Scholar] [CrossRef]
  57. Patanè, D.; Aiuppa, A.; Aloisi, M.; Behncke, B.; Cannata, A.; Coltelli, M.; Salerno, G. Insights into magma and fluid transfer at Mount Etna by a multiparametric approach: A model of the events leading to the 2011 eruptive cycle. J. Geophys. Res. 2013, 118, 3519–3539. [Google Scholar] [CrossRef]
Remotesensing 14 04006 g001 550
Figure 1. (a) GoogleEarth map of southern Italy and Sicily, with the white rectangle showing the area of Mount Etna framed in (b). (b) GoogleEarth map of Mount Etna, with the position of the monitoring devices used in this paper. The yellow dots are the visible cameras, the red dots are the thermal cameras, the green triangle is the strainmeter, and the blue squares are the seismo-acoustic stations, with ESLN being the Serra La Nave reference station. The green squares are the seismic stations. The white square shows the position of the summit craters magnified in (c). (c) GoogleEarth map of Etna’s summit craters. BN = Bocca Nuova; NEC = NE Crater; VOR = Voragine crater; SEC-NSEC = SE Crater and New SE Crater.
Figure 1. (a) GoogleEarth map of southern Italy and Sicily, with the white rectangle showing the area of Mount Etna framed in (b). (b) GoogleEarth map of Mount Etna, with the position of the monitoring devices used in this paper. The yellow dots are the visible cameras, the red dots are the thermal cameras, the green triangle is the strainmeter, and the blue squares are the seismo-acoustic stations, with ESLN being the Serra La Nave reference station. The green squares are the seismic stations. The white square shows the position of the summit craters magnified in (c). (c) GoogleEarth map of Etna’s summit craters. BN = Bocca Nuova; NEC = NE Crater; VOR = Voragine crater; SEC-NSEC = SE Crater and New SE Crater.
Remotesensing 14 04006 g001
Remotesensing 14 04006 g002 550
Figure 2. (a–c) Thermal images recorded by the ENT camera (the yellow bar is 800 m high) located on the south flank of the volcano at ~15 km from the summit, showing the maximum height of the lava fountains occurring on (a) 13 December 2020 at 22:14 (571 m), (b) 28 February 2021 at 08:30 (3600 m), (c) 12 March 2021 at 08:49 (2400 m). (d–f) Visible images recorded by the ECVH camera located at ~27 km from the summit (the horizontal yellow dotted line indicates approximately 5 km above sea level), showing the ash plumes on (d) 13 December 2020 at 22:14, this being rather diluted, (e) the strong plume on 28 February 2021 at 08:30, (f) the weak to intermediate plume on 12 March 2021 at 08:49. (g) Thermal image recorded by the ENT camera on 13 December 2020 at 23:00 showing from south the small lava flow spreading SW (yellow arrow). The scale is the same as in (a). (h,i) Thermal images from the EMCT camera (the vertical yellow bar is 300 m high) showing from east the lava flows (white) spreading on the upper Valle del Bove on 28 February 2021 at 08:48 (h) and on 12 March 2021 at 10:57 (i).
Figure 2. (a–c) Thermal images recorded by the ENT camera (the yellow bar is 800 m high) located on the south flank of the volcano at ~15 km from the summit, showing the maximum height of the lava fountains occurring on (a) 13 December 2020 at 22:14 (571 m), (b) 28 February 2021 at 08:30 (3600 m), (c) 12 March 2021 at 08:49 (2400 m). (d–f) Visible images recorded by the ECVH camera located at ~27 km from the summit (the horizontal yellow dotted line indicates approximately 5 km above sea level), showing the ash plumes on (d) 13 December 2020 at 22:14, this being rather diluted, (e) the strong plume on 28 February 2021 at 08:30, (f) the weak to intermediate plume on 12 March 2021 at 08:49. (g) Thermal image recorded by the ENT camera on 13 December 2020 at 23:00 showing from south the small lava flow spreading SW (yellow arrow). The scale is the same as in (a). (h,i) Thermal images from the EMCT camera (the vertical yellow bar is 300 m high) showing from east the lava flows (white) spreading on the upper Valle del Bove on 28 February 2021 at 08:48 (h) and on 12 March 2021 at 10:57 (i).
Remotesensing 14 04006 g002
Remotesensing 14 04006 g003 550
Figure 3. Calibrated visible images from the ECV camera at (a1) 07:50, (a2) 08:05, (a3) 09:05 on 28 February 2021. SEVIRI satellite images at (b1) 08:00, (b2) 08:15, (b3) 08:45. (c) Evolution of the eruption column analyzed using the ECV camera (blue points) and the SEVIRI (red points) data on 28 February 2021. Calibrated visible images from the ECV camera at (d1) 07:30, (d2) 08:30, (d3) 10:00 on 12 March 2021. SEVIRI satellite images at (e1) 08:00, (e2) 08:45, (e3) 10:15. (f) Evolution of the eruption column analyzed using the ECV camera (blue points) and the SEVIRI (red points) data on 12 March 2021.
Figure 3. Calibrated visible images from the ECV camera at (a1) 07:50, (a2) 08:05, (a3) 09:05 on 28 February 2021. SEVIRI satellite images at (b1) 08:00, (b2) 08:15, (b3) 08:45. (c) Evolution of the eruption column analyzed using the ECV camera (blue points) and the SEVIRI (red points) data on 28 February 2021. Calibrated visible images from the ECV camera at (d1) 07:30, (d2) 08:30, (d3) 10:00 on 12 March 2021. SEVIRI satellite images at (e1) 08:00, (e2) 08:45, (e3) 10:15. (f) Evolution of the eruption column analyzed using the ECV camera (blue points) and the SEVIRI (red points) data on 12 March 2021.
Remotesensing 14 04006 g003
Remotesensing 14 04006 g004 550
Figure 4. Graphs showing, for the three episodes: (a–c) the seismic RMS (root mean square) amplitude of the resultant vector of the three components at the ESLN station; (d–f) the infrasonic RMS amplitude at the ESLN station; (g–i) the strain; (j,k) the plume’s height (in m above sea level) obtained from the ground monitoring cameras (blue dots) and from SEVIRI satellite (black squares) and compared with the plume area (red line) retrieved from satellite; these data are missing for the 13–14 December 2020 pulses; (l–n) the lava fountain heights (in m above the crater); (o–q) the radiant heat flux from satellite (red line) and the maximum apparent temperature from the ENT camera (black line). The green rectangles mark the lava fountain intervals as in Table 2.
Figure 4. Graphs showing, for the three episodes: (a–c) the seismic RMS (root mean square) amplitude of the resultant vector of the three components at the ESLN station; (d–f) the infrasonic RMS amplitude at the ESLN station; (g–i) the strain; (j,k) the plume’s height (in m above sea level) obtained from the ground monitoring cameras (blue dots) and from SEVIRI satellite (black squares) and compared with the plume area (red line) retrieved from satellite; these data are missing for the 13–14 December 2020 pulses; (l–n) the lava fountain heights (in m above the crater); (o–q) the radiant heat flux from satellite (red line) and the maximum apparent temperature from the ENT camera (black line). The green rectangles mark the lava fountain intervals as in Table 2.
Remotesensing 14 04006 g004
Remotesensing 14 04006 g005 550
Figure 5. (a–f) Evolution over time of location of the volcanic tremor source centroid during 3-day-long intervals comprising the 28F21 and 12M21 episodes. (g–j) Evolution over time of location of infrasound events recorded during the aforementioned intervals. (k–n) Evolution over time of location of infrasound tremor windows recorded during the aforementioned intervals. The black horizontal dashed lines in (a,d,g–n) indicate the coordinates of the three main summit craters (SEC-NSEC, VOR and NEC; see Figure 1c for their location). The color of the dots in (a–f) is related to different times (see the color bars next to (e,f)). The color of the dots in (g–n) indicates the amplitude of infrasound event and tremor (see the color bars next to (i,j,m,n)).
Figure 5. (a–f) Evolution over time of location of the volcanic tremor source centroid during 3-day-long intervals comprising the 28F21 and 12M21 episodes. (g–j) Evolution over time of location of infrasound events recorded during the aforementioned intervals. (k–n) Evolution over time of location of infrasound tremor windows recorded during the aforementioned intervals. The black horizontal dashed lines in (a,d,g–n) indicate the coordinates of the three main summit craters (SEC-NSEC, VOR and NEC; see Figure 1c for their location). The color of the dots in (a–f) is related to different times (see the color bars next to (e,f)). The color of the dots in (g–n) indicates the amplitude of infrasound event and tremor (see the color bars next to (i,j,m,n)).
Remotesensing 14 04006 g005
Remotesensing 14 04006 g006 550
Figure 6. Maps (a,b) and W-E sections (c,d) of Etna showing the locations of the volcanic tremor source centroid (colored dots), of the infrasound events (black circles in maps), and of the infrasound tremor windows (red circles in maps) during the 3-day-long intervals comprising the 28F21 and 12M21 episodes. The color of the dots is related to different times (see color bars next to (c,d)). The radii of the black and red black circles in (a,b) are proportional to the number of locations of infrasonic events and tremor in each grid node (see legend in the bottom left corner of (a,b)).
Figure 6. Maps (a,b) and W-E sections (c,d) of Etna showing the locations of the volcanic tremor source centroid (colored dots), of the infrasound events (black circles in maps), and of the infrasound tremor windows (red circles in maps) during the 3-day-long intervals comprising the 28F21 and 12M21 episodes. The color of the dots is related to different times (see color bars next to (c,d)). The radii of the black and red black circles in (a,b) are proportional to the number of locations of infrasonic events and tremor in each grid node (see legend in the bottom left corner of (a,b)).
Remotesensing 14 04006 g006
Table
Table 1. Features of the INGV-OE monitoring cameras used in this paper.
Table 1. Features of the INGV-OE monitoring cameras used in this paper.
LabelTypePositionRate of AcquisitionDistance from the Craters
ENTThermal cameraNicolosi, South flank,
730 m a.s.l.		1 frame/2 s15.0 km
EMOTThermal cameraLa Montagnola, South flank, 2600 m a.s.l.1 frame/s3.0 km
EMCTThermal cameraMt. Cagliato, East flank, 1160 m a.s.l.1 frame/2 s8.3 km
ECVVisible cameraCatania Nesima, South flank, 35 m a.s.l.1 frame/2 s26.7 km
ECVHVisible cameraCatania Nesima, South flank, 35 m a.s.l.1 frame/min26.7 km
EBVHVisible cameraBronte, NW flank, 970 m a.s.l.1 frame/min13.5 km
Table
Table 2. Data on the three lava fountains selected for this study, with details of the three pulses comprising the first event. Starting time, ending time and duration refer to the lava fountain portion of the episode. ERp = pyroclastic eruption rate (volume of pyroclastic divided by the lava fountain duration [38]). ERl = effusive eruption rate, or lava flow volume divided by the lava effusion duration. IER = instantaneous eruption rate (volume of pyroclastics erupted in 1 min durations), peak values and time when it was measured. Volumes of lava flows were retrieved from satellites, with the asterisk (*) indicating that the lava flow volume of the 14 December 2020 event is cumulative of the whole event, comprising the three eruptive pulses (14 December), and the same applies to the ERl. Hf = mean height of the lava fountain, measured above the crater rim. Hc = maximum height of the eruptive column, measured above sea level, and estimated from satellite. The eruptive column was not detected for the three pulses of 13–14 December 2020. The wind speeds are from the hydrometeorological service of ARPA in Emilia Romagna [33] at 3.1, 5.7 and 12 km a.s.l., respectively. All times are in UTC format.
Table 2. Data on the three lava fountains selected for this study, with details of the three pulses comprising the first event. Starting time, ending time and duration refer to the lava fountain portion of the episode. ERp = pyroclastic eruption rate (volume of pyroclastic divided by the lava fountain duration [38]). ERl = effusive eruption rate, or lava flow volume divided by the lava effusion duration. IER = instantaneous eruption rate (volume of pyroclastics erupted in 1 min durations), peak values and time when it was measured. Volumes of lava flows were retrieved from satellites, with the asterisk (*) indicating that the lava flow volume of the 14 December 2020 event is cumulative of the whole event, comprising the three eruptive pulses (14 December), and the same applies to the ERl. Hf = mean height of the lava fountain, measured above the crater rim. Hc = maximum height of the eruptive column, measured above sea level, and estimated from satellite. The eruptive column was not detected for the three pulses of 13–14 December 2020. The wind speeds are from the hydrometeorological service of ARPA in Emilia Romagna [33] at 3.1, 5.7 and 12 km a.s.l., respectively. All times are in UTC format.
Date and
Acronym		Starting Time
(hh:mm)		Ending Time
(hh:mm)		Duration
(min.)		Volume of Pyroclastics
(1 × 106 m3)		Volume of Lava Flows
(1 × 106 m3)		ERp
(m3 s−1)		ERl
(m3 s−1)		IER
(m3 s−1)
(hh:mm)		Hf
(m)		Hc (km)Wind Speed
(m s−1)
13 December 2020
13D20		22:0022:48480.24 83.33 135
(22:14)		231--
13–14 December 2020
13–14D20		23:5800:11130.07 89.74 120
(00:01)		235-11.3
13.3
45.5
14 December 2020
14D20		01:0201:40380.130.79 *57.0269.29 *85
(01:08–01:18)		121-
28 February 2021
28F21		07:4008:34540.701.45216.05377.60338
(08:30)		137612.61.5
13.6
18.8
12 March 2021
12M21		06:4009:451851.632.40146.85130.72276
(08:49)		114910.55.5
10.8
12.3
Table
Table 3. Quantitative parameters describing the three lava fountains selected for this study, derived from seismo-acoustic, strain and column height time series.
Table 3. Quantitative parameters describing the three lava fountains selected for this study, derived from seismo-acoustic, strain and column height time series.
Date and
Acronym		Max Seismic Amplitude (10−5 m s−1)Cumul. Seismic Amplitude (m)Seismic Slope
(10−8 m s−2)		Max infrasonic Amplitude (Pa)Cumul. Infrasonic Amplitude (Pa s)Infrasonic Slope
(10−4 Pa/s)		Strain Amplitude (Nanostrain)Strain Slope (Nanostrain min−1)Max Strain Rate
(Nanostrain min−1)		COLUMN Height Rate
(m s−1)
13–14 December 2020
13D20
13–14D20
14D20		4.880.371.091.7511,7092.5976.1−1.4−2.6-
28 February 2021
28F21		7.160.223.813.58766115.94228.5−3.8−11.12.7
12 March 2021
12M21		10.790.881.113.4526,0294.01169.5−1.3−1.91.5
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Calvari, S.; Biale, E.; Bonaccorso, A.; Cannata, A.; Carleo, L.; Currenti, G.; Di Grazia, G.; Ganci, G.; Iozzia, A.; Pecora, E.; et al. Explosive Paroxysmal Events at Etna Volcano of Different Magnitude and Intensity Explored through a Multidisciplinary Monitoring System. Remote Sens. 2022, 14, 4006. https://doi.org/10.3390/rs14164006

AMA Style

Calvari S, Biale E, Bonaccorso A, Cannata A, Carleo L, Currenti G, Di Grazia G, Ganci G, Iozzia A, Pecora E, et al. Explosive Paroxysmal Events at Etna Volcano of Different Magnitude and Intensity Explored through a Multidisciplinary Monitoring System. Remote Sensing. 2022; 14(16):4006. https://doi.org/10.3390/rs14164006

Chicago/Turabian Style

Calvari, Sonia, Emilio Biale, Alessandro Bonaccorso, Andrea Cannata, Luigi Carleo, Gilda Currenti, Giuseppe Di Grazia, Gaetana Ganci, Adriana Iozzia, Emilio Pecora, and et al. 2022. "Explosive Paroxysmal Events at Etna Volcano of Different Magnitude and Intensity Explored through a Multidisciplinary Monitoring System" Remote Sensing 14, no. 16: 4006. https://doi.org/10.3390/rs14164006

APA Style

Calvari, S., Biale, E., Bonaccorso, A., Cannata, A., Carleo, L., Currenti, G., Di Grazia, G., Ganci, G., Iozzia, A., Pecora, E., Prestifilippo, M., Sciotto, M., & Scollo, S. (2022). Explosive Paroxysmal Events at Etna Volcano of Different Magnitude and Intensity Explored through a Multidisciplinary Monitoring System. Remote Sensing, 14(16), 4006. https://doi.org/10.3390/rs14164006

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop