ZY-1 02D Hyperspectral Imagery Super-Resolution via Endmember Matrix Constraint Unmixing

Abstract

This paper proposes an endmember matrix constraint unmixing method for ZY-1 02D hyperspectral imagery (HSI) super-resolution reconstruction (SRR) to overcome the low resolution of ZY-1 02D HSI. The proposed method combines spectral unmixing and adds novel smoothing constraints to traditional non-negative matrix factorization to improve details and preserve the spectral information of traditional SRR methods. The full utilization of the endmember spectral matrix and endmember abundance matrix of HSI and multispectral imagery (MSI) reconstructs the high spatial resolution and high spectral fidelity HSI. Furthermore, given the ZY-1 02D HSI infrared bands are seriously corrupted by noise, the influence of denoising on the SRR accuracy is also discussed. Experiments show that the proposed method restores spatial details and spectral information and is robust for noise, preserving more spectral information. Therefore, the proposed method is a ZY-1 02D HSI SRR method with high spatial resolution and high spectral fidelity, which improves the spatial resolution while simultaneously solving spectral mixing and provides the possibility for the data further expansion.

1. Introduction

The ZY-1 02D Satellite, a 5 m optical satellite, is the first Chinese operational civil hyperspectral satellite [1]. It can effectively obtain MSI and HSI concurrently, meeting the needs for natural resource management, ecological monitoring, urban and rural construction, emergency management, and other related applications [2]. However, the current payload scale and development costs limit the high spatial resolution of the ZY-1 02D HSI, leading to spectral mixing and limiting the resolvability and quantitative analysis of complex ground objects. The applicability of ZY-1 02D HSI may be further expanded by enhancing its spatial resolution [3].

Present techniques for improving HSI spatial resolution can be categorized as: hardware-based, software-based, and methods combining hardware and software. Hardware-based methods improve the spatial resolution of HSI by directly reducing the pixel size, increasing the number of pixels per unit area by sensor manufacturing techniques [4], or implementing hardware accelerators in field-programmable gate array (FPGA) devices [5,6,7]. Concerning the high cost and limitations of resolution enhancement through hardware-based techniques [8], scholars have undertaken a great deal of research concerning the combination of hardware and software approaches, which generally enhances the HSI spatial resolution by changing the angle of the Charge Coupled Device (CCD) and joint image processing algorithm [9,10,11]. However, these methods can only be used for specific imagery due to the sensor’s sampling method. Furthermore, the high cost of improving the HSI spatial resolution using hardware has made lower-cost software-based techniques more popular with scholars, among which SRR is widely used [12].

Image SRR is a signal processing technology that reconstructs high-resolution images from low-resolution images suffering from noise, blurring, and aliasing effects [4,13]. Over the past several decades, many SRR methods have been proposed under different frameworks, including component substitution (CS), Bayesian, deep learning (DL), and sparse representation (SR) [14]. CS includes such methods as Gram–Schmidt and principal component analysis (PCA). Although promoting the SRR efficiency, Gram–Schmidt results highly depend on the simulated HSI [15]. PCA-based methods have been popular for spectral transformation because the first principal component consists of the most variance, making it a suitable choice to replace the panchromatic component [16]. However, this method creates more spectral artifacts for imageries consisting of vegetation [17]. Gonzalez-Audicana et al. proposed a pan-sharpening method based on a merger of a wavelet–PCA to overcome this issue. However, their approach only utilizes the details of the first principal component replaced by the details of the PAN imagery [18] while ignoring the relationship between variance and correlation. Shah et al. overcome this limitation with an adaptive PCA-contourlet approach for pan-sharpening [17]. PCA-contourlet provides more effective spatial transformation than wavelet during pan-sharpening. However, such CS-based approaches often introduce spectral distortions in the SRR [19].

Bayesian-based SRR often finds the maximization posteriori estimator by combining the likelihood function and the defined appropriate image prior; for example, Zou et al. developed a Bayesian dictionary learning method for HSI SRR in the presence of mixed Poisson-Gaussian noise [20]. Vella et al. improved imagery quality by integrating learning and model-based methods to fuse the HSI and MSI, guaranteeing consistency in the spatial and spectral measurements [21]. Bungert et al. presented a novel model for simultaneous imagery fusion and blind deblurring of HSI based on the total directional variation, achieving good results on real remote sensing data from plant sciences and urban monitoring [22]. Akhtar et al. proposed an HSI SRR approach that fuses high-resolution imagery with low-resolution HSI using non-parametric Bayesian sparse representation [23]. However, these methods require prior knowledge depending on assumptions, so they are not always flexible to adapt to different HSI structures [24].

Since DL has been demonstrated to be very effective in object detection [25,26,27,28], classification [29,30,31], and natural image super-resolution [32,33,34], many researchers have introduced DL into HSI SRR. Using a deep HSI denoiser to leverage both domain knowledge likelihood and deep image prior, Dong et al. designed an iterative HSI SRR algorithm with excellent generalization [35]. Wei et al. introduced a novel deep recursive network for HSI SRR, with a fully end-to-end HSI structure with improved spectral reconstruction results [36]. Zheng et al. enhanced the computation of prior point spread function (PSF) and spectral response function (SRF) in SRR by using an unsupervised DL-based fusion method HyCoNet [37]. Yao et al. enhanced HSI spatial resolution through high spatial resolution MSI by cross-attention mechanism-based coupled unmixing network CUCaNet [38]. Inspired by the non-negative matrix factorization, Liu et al. designed an unsupervised MIAE network for HIS SRR [39]. Admittedly, these methods need an auxiliary higher resolution co-registered imagery, which is sometimes unavailable [40]. For this reason, Wang et al. proposed a novel dilated projection correction network aeDPCN using single low-resolution HIS for SRR [41]. However, DL-based methods often require many samples to train deep neural networks, which limits their application in specific scenarios. Training an excellent deep neural network also takes a lot of time [24].

Combined with matrix decomposition and spectral unmixing, SR-based methods have been widely used for HSI SRR in recent years, which have improved the spatial resolution and solved the spectral mixing of HSI [19,42]. Dong et al. proposed a non-negative structured sparse representation (NSSR) approach for HSI SRR [43]. However, the structured SR is only used to estimate the coefficient matrix, not for the spectral dictionary learning. To improve accuracy, Guo et al. proposed a non-negative clustering-based sparse representation (NNCSR) model [44], which jointly estimates hyperspectral dictionary and the sparse coefficients based on the spatial-spectral sparsity of the HSI. Yet they often ignore the original structure of HSI [45]. To fully consider the spatial/spectral subspace low rank relationships between available HSI/MSI and latent HSI, Xue et al. presented a novel structured sparse low-rank representation (SSLRR) method for HSI SRR [46]. Zhang et al. proposed an HSI and MSI fusion framework based on a novel group spectral embedding by exploring the multiple manifold structures of spectral bands and the low-rank structure of HSI [47]. Yokoya et al. used coupled non-negative matrix factorization (CNMF) to obtain high-resolution HSI, using non-negative matrix factorization to obtain the endmember spectral matrix and the endmember abundance matrix of HSI and MSI [48]. Borsoi et al. proposed an HSI and MSI fusion algorithm with spectral variability (FuVar) to reconstruct high-resolution HSI, employing an unmixing-based formulation and accounting for spectral mismatches between the two imageries [49]. Lanaras et al. presented an SRR method (ICCV15) using joint unmixing of the input HSI and MSI into the pure reflectance spectra of the observed materials and the associated mixing coefficients [50]. However, using only a spectral dictionary is insufficient for preserving spatial information and vice versa [14]. Therefore, Han et al. addressed the problem by fusing HSI and MSI-based optimized dictionaries [51]. Akhtar et al. proposed an SR-based approach (ECCV14) for HSI SRR [52]. Li et al. introduced a spatial group sparsity regularization unmixing-based method for HSI SRR, which obtained high-resolution imagery by entirely using the sparsity and deconvolution matrix of HSI [53].

This study aims to enhance the spatial resolution of ZY-1 02D HSI using the SRR method. Although most SRR methods have realized high reconstruction accuracy previously, they were usually applied in the simulated data, in which the proportion among the fusing imageries is an integer. Unfortunately, the ZY-1 02D imageries lack this integer proportion characteristic due to the inherent limitations during acquisition. Consequently, these methods perform poorly when applied to such data. In addition, ZY-1 02D HSI includes substantial noise in the infrared bands leading to poor data quality.

To overcome these difficulties, we propose an endmember matrix constraint unmixing SRR method in this research. Firstly, the proposed method reconstructs ZY-1 02D HSI with high spatial resolution and high spectral fidelity by adding novel smoothing constraint terms in non-negative matrix factorization. Thus, preserving more information on the endmember matrices. Secondly, the unmixing-based theory makes the proposed method remove noise available while improving the resolution.

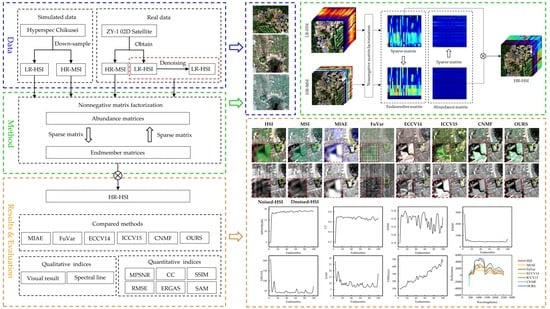
2. Materials and Methods

This section presents the data, the proposed SRR methods, and the quality measures used in the research.

2.1. Data

Two datasets are used in the approach: Hyperspec-VNIR Chikusei and ZY-1 02D.

Hyperspec Chikusei is an airborne HSI dataset acquired by Headwall Hyperspec-VNIR-C imaging sensor (Headwall Photonics Inc., located in Bolton, MA, USA) over agricultural and urban areas in Chikusei, Ibaraki, Japan, on 29 July 2014. It comprises 128 bands in the spectral range from 363 to 1018 nm and 2517 × 2335 pixels with a GSD of 2.5 m [54]. We selected an image of the dimension 540 × 420 pixels for this experiment (Figure 1a).

The ZY-1 02D Satellite contains MSI and HSI in the same time–space. The HSI data has a spatial resolution of 30 m, 166 spectral bands, and a spectral range of 400~2500 nm. The MSI data has a spatial resolution of 10 m, eight spectral bands, and a spectral range of 486~959 nm. Therefore, we selected MSI with 600 × 600 pixel size (Figure 1b) and HSI with 178 × 198 pixel size (Figure 1c) for the experiment.

2.2. Methods

This section introduces the proposed method’s theoretical basis and the quality indices used in SRR.

2.2.1. HSI SRR by Endmember Matrix Constraint Unmixing

The proposed SRR method estimates unobserved high-spatial-resolution HSI (HR-HSI) $Z\in R^{B_h\times P_m}$ from observable low-spatial-resolution HSI (LR-HSI) $X\in R^{B_h\times P_h}$ and high-spatial-resolution MSI (HR-MSI) $Y\in R^{B_m\times P_m}$. $B_m$ and $B_h$ denote the number of spectral channels of multispectral and hyperspectral sensors and $P_m$ and $P_h$ denote the number of pixels of HR-MSI and LR-HSI, respectively. Moreover $B_m\ll B_h$, $P_m\ll P_h$. We assume that the data has been denoised, radiometrically corrected, and geometrically corrected.

SRR Model

Linear spectral mixture modeling is often used to estimate LR-HSI due to its simplicity and efficiency. The model considers HSI a linear combination of a certain number of pure endmembers. Therefore, $Z$ can be formulated as follows:

$$Z=WH+N$$

(1)

• $W\in R^{B_h\times D}$ is the spectral signature matrix, with each column vector representing the endmember spectrum and $D$ being the number of endmembers.
• $H\in R^{D\times P_m}$ is the abundance matrix, with each column vector denoting the abundance fractions of all endmembers at each pixel.
• $D\in R^{B_h\times P_m}$ is the residual.

In practical applications, HR-HSI can be reconstructed only by solving $W$ and $H$.

The solution of Equation (1) relies on the original LR-HSI and HR-MSI in the SRR. However, according to the sensor observation model proposed by Yokoya et al. [48], LR-HSI can be a degenerate form of HR-MSI in the spatial dimension; and HR-MSI can be a degenerate form of HR-HSI in the spectral dimension. Consequently, $X$ and $Y$ can be modeled as:

$$X=ZS+E_s,$$

(2)

$$Y=MZ+E_m,$$

(3)

• $S\in R^{B_m\times B_h}$ is the spatial spread transform matrix, with each column vector representing the transformation of the PSF from the MSI to the HSI.
• $M\in R^{P_m\times P_h}$ is the spectral response transform matrix, with each row vector representing the transformation of the SRF from the hyperspectral sensor to the multispectral for each band.
• $S$ and $M$ are sparse matrices composed of non-negative components.
• $E_m$ and $E_s$ are the residuals.

Putting Equation (1) into (2) and (3), we can get:

$$X\approx W{H}_h,$$

(4)

$$Y\approx W_{m}H,$$

(5)

• $H_h\in R^{D\times P_h}$ denotes the spatially degraded abundance matrix.
• $W_m\in R^{B_m\times D}$ denotes the spectrally degraded endmember matrix.

They can be described as:

$$H_h=HS,$$

(6)

$$W_m=MW,$$

(7)

Endmember Matrix Constraint Unmixing

Based on the non-negative matrix factorization theory, the proposed method iteratively updates the endmember spectral matrix and endmember abundance matrix decomposed from the LR-HSI and HR-MSI until the required HR-HSI is solved. It can be represented by the Figure 2.

To maintain the spectral information and spatial details of the SRR results in processing the real data, we add sparse constraint terms based on the CNMF [48]. Consequently, the proposed SRR model can be expressed using the following formulas:

$$\underset{X,H_h}{\min }=\left\{{\Vert X-W{H}_h\Vert }_F^2+\alpha J_1(H_h)\right\},$$

(8)

$$\underset{W_m,Y}{\min }=\left\{{\Vert Y-W_{m}H\Vert }_F^2+\beta J_2(W_m)\right\},$$

(9)

• $W_m\ge 0$ and $H_h\ge 0$.
• ${\Vert •\Vert }_F$ denotes F-norm.
• $J_1(H_h)$ and $J_2(W_m)$ are penalty terms constraining the solution of the formulas.
• $\alpha$ and $\beta$ are their corresponding Lagrange multipliers, or the regularization parameters. The solution efficiency of different penalty terms varies from different actual problems.

In addition, according to the research of Pauca et al. [55], in each iteration step, a small positive number $\sigma$ is added to the denominator as an adjustment. This study sets $\sigma =1\times {10}^{-9}$ in the experiment. Therefore, the final update criterion is as follows:

$$H_h^{\left(t\right)}=H_h^{\left(t-1\right)}\frac{W^{T}H-\alpha H_h^{(t-1)}}{W^{T}W{H}_h+\sigma },$$

(10)

$$W^{(t)}=W^{(t-1)}\frac{X{H}_h^T}{W{H}_h{H}_h^T+\sigma },$$

(11)

$$W_m^{\left(t\right)}=W_m^{\left(t-1\right)}\frac{Y{H}^T-\beta W_m^{(t-1)}}{W_{m}H{H}^T+\sigma },$$

(12)

$$H^{(t)}=H^{(t-1)}\frac{W_m^{T}Y}{W_m^T{W}_{m}H+\sigma },$$

(13)

2.2.2. Quality Measures

We use the following six complimentary and widely used quality indices for the quantitative SRR assessment: (1) mean peak signal-to-noise ratio (MPSNR); (2) cross-correlations (CC); (3) structure similarity index (SSIM); (4) root mean squared error (RMSE); (5) relative dimensionless global error in synthesis (ERGAS); and (6) spectral angle mapper (SAM). Lagger MPSNR, SSIM, CC and smaller RMSE, ERGAS, SAM, indicates better SRR results. The definitions are as follows:

$$MPSNR({\widehat{X}}_i,X_i)=\frac{1}{B}10{\log }_{10}\left(\frac{\max {(x_i)}^2}{{\Vert {\widehat{x}}_i-x_i\Vert }_2^2/P}\right),$$

(14)

$$SSIM(\widehat{X},X)=\frac{\left(2{\mu }_{\widehat{X}}{\mu }_X+C_1\right)\left(2{\sigma }_{\widehat{X}X}+C_2\right)}{\left({\mu }_{\widehat{X}}^2+{\mu }_X^2+C1\right)\left({\sigma }_{\widehat{X}}^2+{\sigma }_X^2+C_2\right)},$$

(15)

$$CC(\widehat{X},X)=\frac{1}{m_{\lambda }}{\displaystyle \sum _{i=1}^{m_{\lambda }}CCS\left({\widehat{X}}^i,X^i\right)},$$

(16)

$$RMSE(\widehat{X},X)=\frac{{\Vert \widehat{X}-X\Vert }_F^2}{P_m{B}_h},$$

(17)

$$ERGAS(\widehat{X},X)=100d\sqrt{\frac{1}{B}{\displaystyle \sum _{i=1}^B\frac{{\Vert {\widehat{x}}_i-x_i\Vert }_F^2}{{\left(\frac{1}{P}{1}_P^T{x}_i\right)}^2}}},$$

(18)

$$SAM({\widehat{X}}_j,X_j)=\arccos \left(\frac{{\widehat{x}}_j^T{x}_j}{{\Vert {\widehat{x}}_j\Vert }_2^{}{\Vert {\mathrm{x}}_j\Vert }_2^{}}\right),$$

(19)

3. Experiment Results

Many aforementioned methods such as the single-image-based methods are more practical for SRR. However, the ZY-1 02D satellite can effectively obtain MSI and HSI concurrently, providing auxiliary higher resolution co-registered imagery. Therefore, the proposed method is based on the fusion mechanism. In addition, five methods, with the same theoretical basis, are compared to evaluate the performance of our method. All these methods can be divided into DL- and model-based approaches. The DL-based method is MIAE [39]. The model-based methods are FuVar [49], ECCV14 [52], ICCV15 [50], CNMF [48], and our method.

3.1. The Simulated Data

The experiments were performed on Hyperspec Chikusei data. Firstly, the HR-HSI was down-sampled to obtain the simulated LR-HSI and HR-MSI [56]. Then, the SRR results were compared with the original HR-HSI to verify the effectiveness of the proposed method.

Figure 3 shows the results of SRR in the Hyperspec Chikusei simulated data. The RGB bands used in the color composite imagery of HSI and MSI are 55, 37, 22, and 4, 3, and 2, respectively. The color-composite error images (Figure 3b) visualize the spatial distribution of errors in RGB bands, where blue pixels mean no fusion error and colored pixels indicate local spectral distortion. It is essential to reveal the error characteristics of individual bands, because they significantly impact many applications based on spectral indices and band ratios that select very few specific bands [56]. The RMSE images visualize the magnitude of the error at each pixel spectrum. The SAM images visualize the spatial distribution of spectral angle errors.

The FuVar has the most prominent error in the color-composite error, RMSE, and SAM images. The reason is that many parameters in FuVar need to be known or estimated previously. Thus, the FuVar is sensitive to prior knowledge, leading to poor performance only using the available LR-HSI and HR-MSI. For the other five methods, finding the differences from the color composite imageries in Figure 3a is challenging. However, Figure 3b,d show that MIAE has a relatively large error, and then ICCV15 and ECCV14, CNMF and the proposed method have better and approximate results.

Table 1. Quantitative indices of SRR in Hyperspec Chikusei simulated data.

Method	MPSNR	CC	SSIM	RMSE	ERGAS	SAM	TIME (s)
MIAE	31.9489	0.9624	0.8888492	184.37565	17.3296	2.3846	325.1728
FuVar	19.7156	0.5038	0.3319486	791.5662	56.8757	21.4455	1861.6585
ECCV14	13.4956	0.9870	0.0000111	1680.3724	114.5954	1.4832	1302.0734
ICCV15	13.4956	0.9868	0.0000111	1680.3726	114.5954	1.3751	357.9853
CNMF	47.3551	0.9890	0.9999995	0.0039	1.5966	1.3619	240.6289
OURS	47.4468	0.9896	0.9999996	0.0037	1.5117	1.3305	253.2515

presents the quantitative evaluation indices of the SRR results of the six methods, which quantify the SRR abilities from space, spectra, and time, respectively. According to the function of each evaluation index in Section 2.2.2, the proposed method achieves the best results except the time. At the same time, CNMF achieves the highest time efficiency compared with other methods. The reason is that the added constraint items of the proposed method require extra solving time.

Figure 4 shows the variation in the six indices with the number of endmembers in the Hyperspec Chikusei simulated data of the proposed method. The performance of the proposed method improves with an increase in the number of endmembers finally saturating. Furthermore, results indicate that time efficiency is proportional to the number of endmembers. According to the characteristics of HSI, this is reasonable because a linear combination of more varying endmember spectra enables a more accurate expression of all pixel spectra in the data until the endmember variety becomes sufficient. Owing to the abundance sum-to-one, the optimal endmember D may be larger than the actual object types in the scene. This leads to the calculated number of pure endmembers that include not only single objects but also shadows and mixed pixels [48]. Therefore, the number of pure endmembers may exceed the object types in the imagery. We conclude that 30 endmembers has the best performance when the proposed method is applied to the Hyperspec Chikusei simulated data.

Table 2. Effect of the constraints on the proposed method in the Hyperspec Chikusei simulated data.

$\mathit{\alpha }$$\mathbf{and} \mathit{\beta }$ Values	MPSNR	CC	SSIM	RMSE	ERGAS	SAM	TIME (s)
0.00	47.2463	0.9890	0.9999995	0.0039	1.5688	1.3580	273.4078
0.05	47.2376	0.9892	0.9999995	0.0039	1.5438	1.3647	281.8419
0.10	47.2711	0.9890	0.9999995	0.0039	1.5576	1.3695	280.2361
0.15	47.2951	0.9890	0.9999995	0.0039	1.5646	1.3709	250.1167
0.30	47.4468	0.9896	0.9999996	0.0037	1.5117	1.3305	253.2515
0.40	47.3949	0.9889	0.9999995	0.0039	1.5794	1.3799	256.5485
0.50	47.3993	0.9890	0.9999995	0.0039	1.5761	1.3732	257.3367
0.60	47.4953	0.9890	0.9999995	0.0039	1.5673	1.3677	281.2979

illustrates the effect of the constraints on the proposed method in the Hyperspec Chikusei simulated data. $\alpha$ and $\beta$ were set as 0.00, 0.05, 0.10, 0.15, 0.30, 0.40, 0.50, and 0.60 respectively, and fixed endmembers at 30. We conclude that with the increase in the $\alpha$ and $\beta$, the indices gradually become better, but the quality of the SRR results begins declining when $\alpha$ and $\beta$ are 0.40. This decline is due to using the multiplicative update principle in this method, which is a gradient descent criterion with a variable step size. Namely, $\alpha$ and $\beta$ affect the gradient step size, affecting the smoothness of the solutions of Equations (8) and (9). Accordingly, the appropriate $\alpha$ and $\beta$ can ensure the method converges at the optimal point to the greatest extent. Furthermore, the time efficiency of the proposed methods is comparable when $\alpha$ and $\beta$ are between 0.15 and 0.50, especially with 0.15 taking the shortest time. To summarize, the proposed method has the best SRR results when $\alpha$ and $\beta$ are 0.30.

3.2. ZY-1 02D HSI

Figure 5 presents the SRR results of the six methods on ZY-1 02D HSI. The RGB bands used in the color composite imagery of HSI and MSI are 35, 19, 11, and 4, 3, 2, respectively. Obviously, the FaVur has the relatively poorest SRR result. It produced a “mosaic” result with the lowest reconstructed quality. MIAE and ECCV14 reconstruct the spatial details but result in massive spectral distortion; significant differences exist between the SRR result and the original HSI in the color composite imagery. On the contrary, ICCV15 has good spectral fidelity but poor spatial details. Nevertheless, CNMF and the proposed method all achieve better results in spatial and spectral dimensions; furthermore, the spatial resolution of the reconstructed HSI was significantly improved, and the color information of the ground objects is correct. However, the CNMF inadequately solves the mixed spectrum at some edges and does not recover the spatial detail well.

Figure 6 shows the spectral lines of ZY-1 02D HSI SRR results for different methods: vegetation, soil, and blue-roofed building. Compared with the original HSI spectral lines, MIAE fits better for soil but lower for others. FuVar and ICCV14 poorly fit the three types of ground objects. On the other hand, ECCV15 is a better fit for blue-roofed buildings but lower for the others. The fitting effect of CNMF and the proposed method is similar, but the proposed method is higher for blue-roofed buildings.

Table 3. Quantitative indices of SRR in ZY-1 02D HSI.

Method	MPSNR	CC	SSIM	RMSE	ERGAS	SAM	TIME (s)
MIAE	17.8093	0.7392	0.4168	476.9396	60.6493	11.4362	616.3177
FuVar	11.0014	0.2747	0.0811	1203.2809	84.7249	44.2109	4812.1460
ECCV14	10.8087	0.5921	0.0843	1191.3784	87.8039	25.2693	2966.4885
ICCV15	18.8991	0.6769	0.0903	468.8753	42.3810	8.3175	188.3746
CNMF	18.2901	0.6937	0.2494	489.3940	41.8792	11.1107	150.0200
OURS	19.1274	0.6839	0.2478	443.3611	39.4557	7.2542	153.2204

presents the quantitative evaluation indices of the six methods SRR results in the ZY-1 02D HSI. According to the function of each evaluation index in Section 2.2.2, MIAE achieves the best CC and SSIM. The reason is that the imagery sizes of HSI and MSI used in the experiment are 178 × 198 and 600 × 600 pixels, respectively; therefore, the imagery size of the reconstructed HR-HSI is 600 × 600. In addition, there is no reference HR-HSI for the ZY-1 02D data, the original LR-HSI is selected to qualify the method’s performance. Additionally, the MIAE SRR result is very similar to the LR-HSI spatially (Figure 5). Thus, the CC and SSIM, which characterize the geometric distortion, to quantify the reconstructed results contain some errors. However, the proposed method achieves the optimal indices for the others. Especially, the ERGAS, which offers a global indication of the quality of a fused imagery [57], achieves the best value. In addition, the CNMF has the highest time efficiency.

Figure 7 shows the variation in the six indices with the number of endmembers in the ZY-1 02D HSI experimental data of the proposed method, which are similar to the performance in the Hyperspec Chikusei simulated data.

The performance of the proposed method improves with an increase in the number of endmembers and finally saturates from Figure 7a,b,d,e. However, Figure 7c shows the apparent fluctuation of SSIM with the increase in the number of endmembers. The reason is that, without the referenced HR-HSI, the original LR-HSI is selected to qualify the method’s performance. Yet significant differences exist between the spatial resolution of LR-HSI and reconstructed HR-HSI. Thus, the SSIM is low and unstable. The SAM also fluctuates in a small range with the endmember variations in Figure 7f, and the values are between 6 and 9 when the endmember is greater than 28. One of the possible reasons is that the resolution between HSI and corresponding MSI of ZY-1 02D is not an integer, so errors may occur during endmember unmixing, resulting in fluctuations in spatial structure and spectral similarity.

Thirty endmembers were used with the proposed method applied to ZY-1 02D experimental data, combining quantitative and qualitative indices.

3.3. ZY-1 02D HSI SRR Results for before and after Denoising

Due to severe noise in infrared bands of ZY-1 02D HSI, denoising is performed before SRR. Admittedly, denoising will affect the high-frequency information of images. Therefore, this section introduces the SRR results before and after denoising of ZY-1 02D HSI from the color composite imageries, single-band imageries, spectral lines, and quantitative evaluation indices.

Figure 8 illustrates the color composite imageries before and after denoising. The bands of color composite imageries of HSI and MSI are the same in Figure 5. Compared with HSI and MSI in Figure 8a, we can conclude that MIAE obtains a relatively blurry scene. FuVar achieves the poorest SRR results whether denoised or not. ECCV14 retains more spatial details than the spectral information from the SRR results before and after denoising. On the contrary, ICCV15 preserves spectral information better than the remaining spatial details and ICCV15 SRR results preserve more spatial details after denoising. Both CNMF and the proposed method have an excellent ability to preserve the spatial detail and spectral information, whether denoised or not.

Comparing SRR results of all noisy single-band imageries before and after denoising (Figure 9 shows the 160th band with the most severe noise corruption), it is revealed that MIAE and FuVar reconstruct the spatial details poorly, but the latter cannot remove the most noise compared to the first. ECCV14 recovers more spatial details before denoising but is incapable of removing noise. While restoring spatial details, ICCV15 also removes most of the noise in the result before denoising. Although noise in the SRR results of ICCV15 are reduced after denoising, some spatial details are lost, such as object edge contours. The SRR results of CNMF and the proposed method before and after denoising remove most of the noise while improving the resolution of the imagery and restoring the edges of objects and spatial details excellently.

Table 4. Quantitative indices of SRR in ZY-1 02D HSI before denoising.

Method	MPSNR	CC	SSIM	RMSE	ERGAS	SAM	TIME (s)
MIAE	15.0415	0.6439	0.0599	696.3550	65.3466	10.8613	619.4395
FuVar	10.9691	0.2757	0.0363	1208.1741	84.0772	43.9273	4408.8130
ECCV14	10.8002	0.5885	0.0857	1187.8724	87.6889	23.7784	2979.5627
ICCV15	18.7260	0.5643	0.0663	479.8861	42.9734	8.5419	173.6451
CNMF	18.7657	0.6957	0.2499	464.5570	39.6662	9.6229	159.7210
OURS	18.5660	0.7072	0.2572	476.7362	40.0394	15.2285	159.2980

shows the quantitative evaluation indices of the six SRR methods results before denoising. According to the function of each evaluation index in Section 2.2.2, ICCV15 achieves the best SAM. Additionally, the MPSNR, RMSE, and ERGAS of CNMF are the best. The CC, SSIM, and time efficiency of the proposed method are the best.

Figure 10 shows the spectral lines of ZY-1 02D HSI SRR results for different materials: vegetation, soil, and blue-roofed building. MIAE best fits the spectral lines of the soil relatively after denoising, but poorly for the others. The three spectral lines of FuVar and ECCV14 fit poorly with original spectral lines both before and after denoising, indicating the highest distortion of its SRR results. ICCV15 has a better-fitted result of the spectral line of the blue-roofed building after denoising. For CNMF, the spectral lines of the blue-roofed building before and after denoising are quite different from the original, while the spectral line of the soil after denoising fits well with the original. Notably, the vegetation spectral line of CNMF after denoising has some outliers. At the same time, the proposed method has the best fitting effect of all three spectral lines after denoising.

4. Discussion

4.1. SRR via Constraint Endmember Matrix Unmixing

Most of the traditional SRR methods are applied to simulated datasets, in which the proportion of resolution between HSI and corresponding MSI is an integer achieving high SRR accuracy. Unfortunately, these methods often achieved lower SRR accuracy when applied to the ZY-1 02D data. Our proposed method added endmember matrix constraint terms to traditional the non-negative matrix factorization, guiding Formulas (8) and (9) to conduct smoothing solutions to improve the usability of SRR on ZY-1 02D data. This measure enables the proposed method to fully utilize the properties of endmember matrices of HSI and MSI during SRR, thereby retaining more spatial details and spectral information.

Spectral unmixing and SRR can amplify each other in an interactive feedback framework. Hence the unmixing-based SRR not only enhances the spatial resolution but also solves the mixing pixels in HSI [58]. Linear spectral mixing (LMM) models are widely used in spectral unmixing with simplicity and efficiency [59]. The endmember abundance mapping in Figure 11 corresponds to easily recognizable surface materials observed in the ZY-1 02D HSI scene. Even though these are not always “pure materials” in the physical sense, they look realistic and comparatively clean due to inter-reflections and shadows. This confirms the conventional wisdom that the LMM is sufficient for many HSI imaging problems, particularly SRR [60].

The quantitative evaluation indices of spectral information of Hyperspec Chikusei simulated data and ZY-1 02D experimental data (Table 1 and Table 3) illustrate that the proposed method achieves the best MPSNR, RMSE, ERGAS, and SAM when compared to other methods. Furthermore, from the visual results (Figure 5) and the spectral line graphs (Figure 6), the proposed method also has less noise and the best spectral line fitting. This improvement is due to the proposed method’s non-negative endmember matrices and sum-to-one constraint, which avoids outliers and artifacts in SRR results [60]. Therefore, the proposed method can realize spectral unmixing during SRR.

To summarize, the proposed SRR method is suitable for ZY-1 02D data, improving the spatial resolution and preserving more spectral information.

4.2. Denoising Effect on SRR for ZY-102D HSI

Since the proposed method is based on spectral unmixing, the predefined number of endmembers is the corresponding subspace. Denoising means reducing the dimension of high-dimensional noisy data, separating noise in a signal subspace [61]. Consequently, subspace-based methods naturally imply denoising ability [57]. The results also logically illustrate that the proposed method can remove most noise during SRR (Figure 8, Figure 9 and Figure 10). However, the proposed method mainly implements SRR. Thus, some bands still contain some noise.

Consequently, we preprocessed the ZY-1 02D HSI noisy bands using subspace-based non-local low-rank and sparse factorization (SNLRSF) [62]. Typically, denoising will change the part of the high-frequency information of the imagery and influence SRR correspondingly. Accordingly, we set up the control experiment to explore whether to denoise previously.

The control experiment results (Section 3.3) reveal that preprocessing the ZY-1 02D HIS noised bands before SRR can preserve more information and achieve better results.

4.3. Future Works

The proposed method adds novel smoothing constraints to non-negative matrix factorization, improving the SRR accuracy for ZY-1 02D HSI. However, small-window images were selected in our experiments instead of the whole scene. Future works will be carried out to extend the proposed method for the whole scenes or realize the adaptive parameter blocking strategy for large-scale scenes to promote the broader application of ZY-1 02D HSI.

5. Conclusions

This study proposed an endmember matrix constraint unmixing method for ZY-1 02D HSI SRR. The proposed method adds endmember matrix constraint terms to the non-negative matrix factorization, which not only enhances the spatial resolution but also realizes the spectral unmixing vastly. In addition, regarding the severe noise in the infrared bands of ZY-1 02D HSI, the influence of denoising on SRR is also discussed. Experimental results on simulated and ZY-1 02D data demonstrate that the proposed method is suitable for ZY-1 02D HSI SRR.