Dictionary Learning- and Total Variation-Based High-Light-Efficiency Snapshot Multi-Aperture Spectral Imaging
Abstract
:1. Introduction
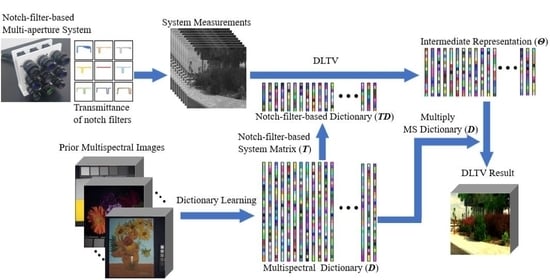
- A multispectral imaging system that combines a notch-filter array and multiple apertures is proposed. The use of notch filters enables the development of a high-light-efficiency imaging system that overcomes the drawbacks of conventional bandpass-filter-based multispectral imaging systems (e.g., low spatial resolutions and imaging speeds). Compared with CASSI or DCCHI systems, the proposed multi-aperture multispectral imaging system enables more spectral information from the target scene to be captured, significantly reducing the complexity of the underdetermined reconstruction problem. Compared with those of other bandpass-filter-based multispectral imaging systems, the higher light efficiency yielded by the notch-filter array significantly improves the imaging quality and temporal resolution of the multispectral imaging system.
- A dictionary learning- and TV-based spectral super-resolution algorithm (DL-TV) is proposed; it can train sparse dictionaries to achieve a high imaging quality as well as reduce noise with TV. Because the proposed method introduces more imaging priors, it can provide better imaging performance than the alternative direction multiplier method (ADMM) [32] with the dictionary learning algorithm (DL) [33].
- The effectiveness of the proposed system and algorithm is demonstrated through simulations using various datasets.
- A snapshot multispectral-imaging prototype system is built to verify real-world imaging performance via indoor experiments and field tests. The experimental results demonstrate that the combination of the proposed imaging system and compressive-sensing-based super-resolution spectral algorithm can obtain high-quality as well as high-spatial-spectral-resolution images.
2. Methods
2.1. Notch Filter Imaging Model
2.2. Spectral Super-Resolution Algorithm
| Algorithm 1: DL-TV for MSI Reconstruction |
| 1: Input: , , , |
| 2: Initialization: , , , , , , ; |
| 3: while do |
| 4: Update via Equation (17) |
| 5: Update via Equation (19) |
| 6: Update via Equation (21) |
| 7: Update via Equation (14) |
| 8: Update via Equation. (15) |
| 9: end while |
| 10: Compute via Equation (17) |
| Output: MSI |
2.3. Prototype System
3. Simulations Using Public Datasets
4. Experiments Using Actual Captured Data
4.1. Indoor Experiments
4.2. Field Tests
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Landgrebe, D. The evolution of Landsat data analysis. Photogramm. Eng. Remote Sens. 1997, 63, 859–867. [Google Scholar]
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V.; Wu, H.-I. Biomedical Optics: Principles and Imaging; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Gat, N.; Subramanian, S.; Barhen, J.; Toomarian, N. Spectral imaging applications: Remote sensing, environmental monitoring, medicine, military operations, factory automation, and manufacturing. In Proceedings of the 25th AIPR Workshop: Emerging Applications of Computer Vision, Washington, DC, USA, 16–18 October 1996; pp. 63–77. [Google Scholar]
- Zhang, M.; Wang, L.; Zhang, L.; Huang, H. High light efficiency snapshot spectral imaging via spatial multiplexing and spectral mixing. Opt. Express 2020, 28, 19837–19850. [Google Scholar] [CrossRef] [PubMed]
- Mu, T.; Han, F.; Bao, D.; Zhang, C.; Liang, R. Compact snapshot optically replicating and remapping imaging spectrometer (ORRIS) using a focal plane continuous variable filter. Opt. Lett. 2019, 44, 1281–1284. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Tian, X.; Ju, H.; Wang, D.; Wu, H.; Ren, L.; Liang, R. Reconfigurable snapshot polarimetric imaging technique through spectral-polarization filtering. Opt. Lett. 2019, 44, 4574–4577. [Google Scholar] [CrossRef] [PubMed]
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Sellar, R.G.; Boreman, G.D. Comparison of relative signal-to-noise ratios of different classes of imaging spectrometer. Appl. Opt. 2005, 44, 1614–1624. [Google Scholar] [CrossRef]
- He, Q.; Wang, R. Hyperspectral imaging enabled by an unmodified smartphone for analyzing skin morphological features and monitoring hemodynamics. Biomed. Opt. Express 2020, 11, 895–910. [Google Scholar] [CrossRef]
- Genser, N.; Seiler, J.; Kaup, A. Camera array for multi-spectral imaging. IEEE Trans. Image Process. 2020, 29, 9234–9249. [Google Scholar] [CrossRef]
- Gehm, M.E.; John, R.; Brady, D.J.; Willett, R.M.; Schulz, T.J. Single-shot compressive spectral imaging with a dual-disperser architecture. Opt. Express 2007, 15, 14013–14027. [Google Scholar] [CrossRef]
- Tao, C.; Zhu, H.; Sun, P.; Wu, R.; Zheng, Z. Hyperspectral image recovery based on fusion of coded aperture snapshot spectral imaging and RGB images by guided filtering. Opt. Commun. 2020, 458, 124804. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, Z.; Gao, D.; Shi, G.; Wu, F. Dual-camera design for coded aperture snapshot spectral imaging. Appl. Opt. 2015, 54, 848–858. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Xiong, Z.; Gao, D.; Shi, G.; Zeng, W.; Wu, F. High-speed hyperspectral video acquisition with a dual-camera architecture. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4942–4950. [Google Scholar]
- Wagadarikar, A.A.; Pitsianis, N.P.; Sun, X.; Brady, D.J. Video rate spectral imaging using a coded aperture snapshot spectral imager. Opt. Express 2009, 17, 6368–6388. [Google Scholar] [CrossRef] [PubMed]
- Oiknine, Y.; August, I.; Stern, A. Multi-aperture snapshot compressive hyperspectral camera. Opt. Lett. 2018, 43, 5042. [Google Scholar] [CrossRef] [PubMed]
- Carles, G.; Chen, S.; Bustin, N.; Downing, J.; McCall, D.; Wood, A.; Harvey, A.R. Multi-aperture foveated imaging. Opt. Lett. 2016, 41, 1869–1872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Gan, L. Block compressed sensing of natural images. In Proceedings of the 15th International Conference on Digital Signal Processing, Cardiff, UK, 1–4 July 2007; pp. 403–406. [Google Scholar]
- Fauvel, S.; Ward, R.K. An energy efficient compressed sensing framework for the compression of electroencephalogram signals. Sensors 2014, 14, 1474–1496. [Google Scholar] [CrossRef] [Green Version]
- Leinonen, M.; Codreanu, M.; Juntti, M. Sequential compressed sensing with progressive signal reconstruction in wireless sensor networks. IEEE Trans. Wirel. Commun. 2014, 14, 1622–1635. [Google Scholar] [CrossRef]
- Candes, E.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Probl. 2007, 23, 969. [Google Scholar] [CrossRef] [Green Version]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef] [Green Version]
- Xue, J.; Zhao, Y.Q.; Bu, Y.; Liao, W.; Chan, J.C.W.; Philips, W. Spatial-spectral structured sparse low-rank representation for hyperspectral image super-resolution. IEEE Trans. Image Process. 2021, 30, 3084–3097. [Google Scholar] [CrossRef] [PubMed]
- Llull, P.; Liao, X.; Yuan, X.; Yang, J.; Kittle, D.; Carin, L.; Sapiro, G.; Brady, D.J. Coded aperture compressive temporal imaging. Opt. Express 2013, 21, 10526–10545. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed Sensing MRI. IEEE Signal Process. Mag. 2008, 25, 72–82. [Google Scholar] [CrossRef]
- Yuan, X. Generalized alternating projection based total variation minimization for compressive sensing. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2539–2543. [Google Scholar]
- Bioucas-Dias, J.M.; Figueiredo, M.A. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef] [Green Version]
- Chambolle, A. An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 2004, 20, 89–97. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Huang, F.; Lin, P.; Wu, X.; Cao, R.; Zhou, B. Compressive Sensing-Based Super-Resolution Multispectral Imaging System. Available online: https://ui.adsabs.harvard.edu/abs/2022SPIE12169E..34H/abstract (accessed on 27 March 2022).
- Lansel, S.; Parmar, M.; Wandell, B.A. Dictionaries for sparse representation and recovery of reflectances. In Proceedings of the IS&T-SPIE Electronic Imaging Symposium, San Jose, CA, USA, 19–20 January 2009. [Google Scholar]
- Parkkinen, J.P.S.; Hallikainen, J.; Jaaskelainen, T. Characteristic spectra of Munsell colors. J. Opt. Soc. Am. A 1989, 6, 318–322. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef] [Green Version]
- Yun, B.I.; Petković, M.S. Iterative methods based on the signum function approach for solving nonlinear equations. Numer. Algorithms 2009, 52, 649–662. [Google Scholar] [CrossRef]
- Singh, D.; Kaur, M.; Jabarulla, M.Y.; Kumar, V.; Lee, H.-N. Evolving fusion-based visibility restoration model for hazy remote sensing images using dynamic differential evolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1002214. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar] [CrossRef] [Green Version]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Yasuma, F.; Mitsunaga, T. Generalized assorted pixel camera: Postcapture control of resolution, dynamic range, and spectrum. IEEE Trans. Image Process. 2010, 19, 2241–2253. [Google Scholar] [CrossRef] [Green Version]
- Arad, B.; Ben-Shahar, O. Sparse recovery of hyperspectral signal from natural RGB images. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 19–34. [Google Scholar]
- Zheng, S.; Liu, Y.; Meng, Z.; Qiao, M.; Tong, Z.; Yang, X.; Han, S.; Yuan, X. Deep plug-and-play priors for spectral snapshot compressive imaging. Photonics Res. 2021, 9, B18–B29. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, H.; Fu, Y. Fast parallel implementation of dual-camera compressive hyperspectral imaging system. IEEE Trans. Circuits Syst. Video Technol. 2018, 29, 3404–3414. [Google Scholar] [CrossRef]
- Tao, C.; Zhu, H.; Wang, X.; Zheng, S.; Xie, Q.; Wang, C.; Wu, R.; Zheng, Z. Compressive single-pixel hyperspectral imaging using RGB sensors. Opt. Express 2021, 29, 11207–11220. [Google Scholar] [CrossRef]
- Gregor, K.; LeCun, Y. Learning fast approximations of sparse coding. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–25 June 2010; pp. 399–406. [Google Scholar]








| MSI | PSNR | SSIM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TwIST [30] | GAP-TV [29] | PnP [45] | DCCHI [15] | DL [33] | DL-TV | TwIST | GAP-TV | PnP | DCCHI | DL | DL-TV | |
| Balloons | 31.941 | 33.530 | 34.215 | 38.970 | 42.039 | 42.630 | 0.950 | 0.943 | 0.955 | 0.990 | 0.990 | 0.993 |
| Beads | 20.788 | 21.873 | 21.870 | 25.189 | 36.586 | 37.030 | 0.568 | 0.558 | 0.559 | 0.825 | 0.966 | 0.969 |
| CD | 29.616 | 31.975 | 31.522 | 34.483 | 32.686 | 32.785 | 0.927 | 0.912 | 0.907 | 0.971 | 0.973 | 0.977 |
| Toy | 23.956 | 24.774 | 24.997 | 34.044 | 42.618 | 43.103 | 0.805 | 0.791 | 0.822 | 0.964 | 0.991 | 0.995 |
| Clay | 31.954 | 32.979 | 32.960 | 36.754 | 44.938 | 46.720 | 0.907 | 0.893 | 0.897 | 0.952 | 0.976 | 0.984 |
| Cloth | 23.292 | 23.517 | 23.942 | 24.825 | 41.492 | 42.523 | 0.490 | 0.486 | 0.500 | 0.800 | 0.982 | 0.985 |
| Egyptian | 32.753 | 32.867 | 32.453 | 43.503 | 48.820 | 50.089 | 0.904 | 0.906 | 0.921 | 0.992 | 0.990 | 0.996 |
| Face | 32.467 | 32.449 | 32.463 | 40.814 | 44.153 | 44.975 | 0.928 | 0.915 | 0.908 | 0.988 | 0.985 | 0.994 |
| Beers | 30.190 | 32.127 | 34.265 | 39.194 | 42.037 | 42.456 | 0.940 | 0.928 | 0.952 | 0.984 | 0.991 | 0.995 |
| Food | 30.282 | 31.186 | 32.114 | 36.643 | 44.688 | 45.706 | 0.872 | 0.853 | 0.904 | 0.952 | 0.987 | 0.991 |
| Lemon | 28.853 | 29.733 | 30.695 | 39.833 | 47.357 | 48.458 | 0.871 | 0.841 | 0.874 | 0.975 | 0.991 | 0.994 |
| Lemons | 33.485 | 33.282 | 33.196 | 41.851 | 47.562 | 48.662 | 0.938 | 0.924 | 0.927 | 0.983 | 0.992 | 0.996 |
| Peppers | 28.501 | 30.187 | 30.621 | 36.307 | 44.854 | 45.744 | 0.893 | 0.893 | 0.908 | 0.950 | 0.989 | 0.993 |
| Strawberries | 32.089 | 31.353 | 30.832 | 41.738 | 47.019 | 48.065 | 0.895 | 0.870 | 0.887 | 0.971 | 0.991 | 0.994 |
| Sushi | 31.637 | 32.301 | 32.893 | 40.863 | 46.039 | 46.821 | 0.955 | 0.948 | 0.958 | 0.989 | 0.990 | 0.993 |
| Average | 29.454 | 30.275 | 30.603 | 37.001 | 43.526 | 44.384 | 0.856 | 0.844 | 0.859 | 0.952 | 0.986 | 0.990 |
| MSI | RMSE | SAM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TwIST | GAP-TV | PnP | DCCHI | DL | DL-TV | TwIST | GAP-TV | PnP | DCCHI | DL | DL-TV | |
| Balloons | 6.483 | 5.387 | 4.974 | 2.914 | 2.644 | 2.560 | 0.091 | 0.085 | 0.119 | 0.070 | 0.088 | 0.085 |
| Beads | 23.518 | 20.702 | 20.709 | 14.366 | 4.877 | 4.738 | 0.304 | 0.311 | 0.310 | 0.313 | 0.109 | 0.104 |
| CD | 8.498 | 6.455 | 6.807 | 4.848 | 7.286 | 7.204 | 0.121 | 0.134 | 0.193 | 0.094 | 0.130 | 0.127 |
| Toy | 16.240 | 14.781 | 14.399 | 5.554 | 2.259 | 2.175 | 0.182 | 0.187 | 0.210 | 0.125 | 0.085 | 0.075 |
| Clay | 6.673 | 5.917 | 5.864 | 3.859 | 1.712 | 1.562 | 0.190 | 0.228 | 0.316 | 0.156 | 0.148 | 0.124 |
| Cloth | 17.631 | 17.118 | 16.405 | 15.964 | 3.032 | 2.878 | 0.171 | 0.172 | 0.171 | 0.318 | 0.081 | 0.080 |
| Egyptian | 5.934 | 5.832 | 6.103 | 1.716 | 1.172 | 1.084 | 0.264 | 0.255 | 0.347 | 0.113 | 0.172 | 0.140 |
| Face | 6.113 | 6.107 | 6.086 | 2.400 | 1.908 | 1.823 | 0.131 | 0.144 | 0.244 | 0.087 | 0.108 | 0.095 |
| Beers | 7.917 | 6.329 | 4.952 | 2.915 | 2.501 | 2.413 | 0.044 | 0.041 | 0.042 | 0.033 | 0.038 | 0.038 |
| Food | 7.893 | 7.080 | 6.331 | 3.812 | 1.979 | 1.888 | 0.154 | 0.181 | 0.213 | 0.137 | 0.120 | 0.113 |
| Lemon | 9.259 | 8.344 | 7.460 | 2.656 | 1.364 | 1.264 | 0.177 | 0.229 | 0.254 | 0.143 | 0.108 | 0.099 |
| Lemons | 5.421 | 5.539 | 5.605 | 2.090 | 1.315 | 1.224 | 0.107 | 0.117 | 0.217 | 0.087 | 0.082 | 0.073 |
| Peppers | 9.609 | 7.917 | 7.520 | 3.923 | 1.784 | 1.691 | 0.156 | 0.165 | 0.241 | 0.152 | 0.114 | 0.103 |
| Strawberries | 6.375 | 6.921 | 7.391 | 2.132 | 1.416 | 1.325 | 0.149 | 0.177 | 0.248 | 0.105 | 0.096 | 0.087 |
| Sushi | 6.701 | 6.216 | 5.796 | 2.350 | 1.715 | 1.644 | 0.106 | 0.126 | 0.184 | 0.080 | 0.138 | 0.130 |
| Average | 9.618 | 8.710 | 8.427 | 4.767 | 2.464 | 2.365 | 0.156 | 0.170 | 0.221 | 0.134 | 0.108 | 0.098 |
| MSI | PSNR | SSIM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TwIST | GAP-TV | PnP | DCCHI | DL | DL-TV | TwIST | GAP-TV | PnP | DCCHI | DL | DL-TV | |
| 4cam1640 | 33.015 | 33.094 | 33.632 | 35.419 | 43.257 | 43.817 | 0.857 | 0.842 | 0.845 | 0.963 | 0.992 | 0.994 |
| BGU1113 | 25.628 | 26.814 | 27.912 | 33.257 | 40.845 | 41.251 | 0.785 | 0.770 | 0.796 | 0.960 | 0.990 | 0.992 |
| BGU1136 | 27.366 | 28.047 | 28.765 | 32.470 | 42.085 | 42.230 | 0.801 | 0.790 | 0.838 | 0.963 | 0.994 | 0.995 |
| Flower1336 | 24.876 | 26.054 | 27.235 | 27.001 | 40.061 | 40.459 | 0.676 | 0.677 | 0.714 | 0.905 | 0.987 | 0.988 |
| Labtest1502 | 31.674 | 30.418 | 29.901 | 40.858 | 48.608 | 49.425 | 0.879 | 0.841 | 0.849 | 0.982 | 0.996 | 0.997 |
| Labtest1504 | 37.060 | 37.019 | 37.915 | 42.547 | 52.464 | 53.778 | 0.940 | 0.931 | 0.938 | 0.988 | 0.998 | 0.999 |
| CAMP1659 | 27.165 | 28.585 | 29.365 | 35.412 | 39.474 | 39.738 | 0.863 | 0.853 | 0.850 | 0.977 | 0.993 | 0.995 |
| bgu1459 | 31.275 | 31.042 | 31.788 | 37.235 | 45.490 | 46.376 | 0.831 | 0.819 | 0.833 | 0.968 | 0.989 | 0.990 |
| bgu1523 | 25.717 | 26.944 | 27.325 | 28.526 | 39.883 | 40.109 | 0.763 | 0.754 | 0.798 | 0.930 | 0.988 | 0.989 |
| eve1549 | 33.527 | 34.585 | 35.221 | 38.622 | 44.409 | 44.654 | 0.898 | 0.888 | 0.890 | 0.977 | 0.995 | 0.996 |
| eve1602 | 28.396 | 28.515 | 28.957 | 31.834 | 41.213 | 41.325 | 0.823 | 0.802 | 0.833 | 0.951 | 0.991 | 0.993 |
| gavyam0930 | 32.781 | 31.870 | 31.867 | 40.023 | 45.644 | 45.953 | 0.860 | 0.831 | 0.831 | 0.971 | 0.994 | 0.995 |
| grf0949 | 27.403 | 27.865 | 28.849 | 30.452 | 42.080 | 42.655 | 0.746 | 0.737 | 0.761 | 0.934 | 0.989 | 0.992 |
| hill1219 | 26.995 | 28.057 | 28.656 | 27.617 | 40.198 | 40.699 | 0.735 | 0.729 | 0.740 | 0.913 | 0.987 | 0.989 |
| hill1235 | 28.370 | 29.203 | 29.651 | 28.408 | 39.655 | 40.144 | 0.771 | 0.767 | 0.769 | 0.932 | 0.988 | 0.992 |
| Average | 29.417 | 29.874 | 30.469 | 33.979 | 43.024 | 43.508 | 0.815 | 0.802 | 0.819 | 0.954 | 0.991 | 0.993 |
| MSI | RMSE | SAM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TwIST | GAP-TV | PnP | DCCHI | DL | DL-TV | TwIST | GAP-TV | PnP | DCCHI | DL | DL-TV | |
| 4cam1640 | 5.859 | 5.725 | 5.438 | 4.667 | 2.206 | 2.145 | 0.036 | 0.040 | 0.044 | 0.054 | 0.037 | 0.036 |
| BGU1113 | 13.823 | 11.905 | 10.668 | 5.954 | 2.939 | 2.878 | 0.074 | 0.079 | 0.077 | 0.084 | 0.059 | 0.059 |
| BGU1136 | 11.181 | 10.245 | 9.362 | 6.758 | 2.787 | 2.808 | 0.072 | 0.081 | 0.077 | 0.079 | 0.038 | 0.038 |
| Flower1336 | 14.867 | 12.976 | 11.551 | 12.881 | 3.782 | 3.808 | 0.078 | 0.073 | 0.065 | 0.156 | 0.049 | 0.050 |
| Labtest1502 | 6.810 | 7.726 | 8.181 | 2.365 | 1.137 | 1.072 | 0.047 | 0.067 | 0.066 | 0.034 | 0.032 | 0.031 |
| Labtest1504 | 3.696 | 3.625 | 3.298 | 2.037 | 0.689 | 0.622 | 0.045 | 0.053 | 0.055 | 0.060 | 0.030 | 0.029 |
| CAMP1659 | 11.262 | 9.612 | 8.931 | 4.793 | 3.874 | 3.888 | 0.056 | 0.053 | 0.054 | 0.050 | 0.040 | 0.041 |
| bgu1459 | 7.307 | 7.280 | 6.788 | 3.712 | 1.992 | 1.930 | 0.075 | 0.092 | 0.092 | 0.078 | 0.068 | 0.067 |
| bgu1523 | 13.244 | 11.537 | 11.000 | 10.660 | 3.832 | 3.875 | 0.069 | 0.061 | 0.064 | 0.130 | 0.055 | 0.056 |
| eve1549 | 5.529 | 4.839 | 4.536 | 3.127 | 2.102 | 2.107 | 0.030 | 0.031 | 0.034 | 0.038 | 0.036 | 0.036 |
| eve1602 | 9.775 | 9.594 | 9.108 | 7.201 | 3.095 | 3.109 | 0.040 | 0.048 | 0.054 | 0.074 | 0.042 | 0.042 |
| gavyam0930 | 6.061 | 6.564 | 6.566 | 2.567 | 1.695 | 1.676 | 0.065 | 0.086 | 0.086 | 0.052 | 0.049 | 0.049 |
| grf0949 | 11.263 | 10.514 | 9.548 | 8.421 | 2.752 | 2.692 | 0.062 | 0.063 | 0.061 | 0.112 | 0.046 | 0.045 |
| hill1219 | 11.601 | 10.321 | 9.772 | 12.098 | 3.695 | 3.657 | 0.053 | 0.049 | 0.053 | 0.122 | 0.060 | 0.059 |
| hill1235 | 9.963 | 9.050 | 8.695 | 11.065 | 3.583 | 3.500 | 0.040 | 0.037 | 0.043 | 0.100 | 0.050 | 0.050 |
| Average | 9.483 | 8.768 | 8.229 | 6.554 | 2.677 | 2.651 | 0.056 | 0.061 | 0.062 | 0.082 | 0.0461 | 0.0459 |
| MSI | σ = 10 | σ = 20 | σ = 40 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |||||||
| DL | DL-TV | DL | DL-TV | DL | DL-TV | DL | DL-TV | DL | DL-TV | DL | DL-TV | |
| Balloons | 32.637 | 36.647 | 0.742 | 0.919 | 29.309 | 34.079 | 0.543 | 0.863 | 25.480 | 30.981 | 0.354 | 0.683 |
| Beads | 30.328 | 31.114 | 0.824 | 0.878 | 27.932 | 28.613 | 0.695 | 0.816 | 24.670 | 27.262 | 0.544 | 0.720 |
| CD | 29.453 | 31.115 | 0.731 | 0.888 | 27.658 | 29.712 | 0.557 | 0.819 | 25.496 | 28.327 | 0.403 | 0.651 |
| Toy | 33.530 | 35.605 | 0.798 | 0.909 | 30.206 | 33.209 | 0.657 | 0.859 | 26.822 | 30.867 | 0.497 | 0.708 |
| Clay | 34.721 | 36.694 | 0.707 | 0.801 | 31.097 | 33.868 | 0.486 | 0.708 | 27.234 | 31.117 | 0.302 | 0.484 |
| Cloth | 32.940 | 34.669 | 0.783 | 0.872 | 28.887 | 31.574 | 0.614 | 0.810 | 24.802 | 29.130 | 0.451 | 0.683 |
| Egyptian | 36.571 | 40.108 | 0.821 | 0.898 | 32.932 | 37.568 | 0.638 | 0.813 | 29.332 | 33.529 | 0.426 | 0.593 |
| Face | 33.951 | 37.119 | 0.678 | 0.855 | 30.709 | 34.559 | 0.501 | 0.785 | 27.385 | 31.465 | 0.336 | 0.571 |
| Beers | 32.084 | 35.147 | 0.699 | 0.914 | 28.083 | 32.388 | 0.464 | 0.857 | 24.156 | 29.726 | 0.271 | 0.673 |
| Food | 34.614 | 35.535 | 0.790 | 0.879 | 30.727 | 32.965 | 0.614 | 0.822 | 26.909 | 30.446 | 0.442 | 0.661 |
| Lemon | 35.024 | 37.947 | 0.787 | 0.908 | 31.475 | 35.422 | 0.641 | 0.857 | 28.026 | 32.204 | 0.480 | 0.699 |
| Lemons | 34.905 | 37.766 | 0.756 | 0.886 | 31.032 | 35.076 | 0.571 | 0.823 | 27.301 | 31.842 | 0.406 | 0.649 |
| Peppers | 34.541 | 35.901 | 0.779 | 0.885 | 30.714 | 33.135 | 0.599 | 0.825 | 26.681 | 30.553 | 0.421 | 0.655 |
| Strawberries | 35.076 | 38.341 | 0.760 | 0.878 | 31.336 | 35.864 | 0.589 | 0.820 | 27.907 | 32.547 | 0.423 | 0.648 |
| Sushi | 36.024 | 38.328 | 0.786 | 0.899 | 32.274 | 36.061 | 0.621 | 0.843 | 29.242 | 32.731 | 0.466 | 0.668 |
| Average | 33.760 | 36.136 | 0.763 | 0.885 | 30.292 | 33.606 | 0.586 | 0.821 | 26.763 | 30.849 | 0.415 | 0.650 |
| Method | TwIST | GPA-TV | PnP | DCCHI | DL | DL-TV |
|---|---|---|---|---|---|---|
| Time | 500.5 | 569.8 | 540.8 | 525.6 | 6.4 | 64.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, F.; Lin, P.; Cao, R.; Zhou, B.; Wu, X. Dictionary Learning- and Total Variation-Based High-Light-Efficiency Snapshot Multi-Aperture Spectral Imaging. Remote Sens. 2022, 14, 4115. https://doi.org/10.3390/rs14164115
Huang F, Lin P, Cao R, Zhou B, Wu X. Dictionary Learning- and Total Variation-Based High-Light-Efficiency Snapshot Multi-Aperture Spectral Imaging. Remote Sensing. 2022; 14(16):4115. https://doi.org/10.3390/rs14164115
Chicago/Turabian StyleHuang, Feng, Peng Lin, Rongjin Cao, Bin Zhou, and Xianyu Wu. 2022. "Dictionary Learning- and Total Variation-Based High-Light-Efficiency Snapshot Multi-Aperture Spectral Imaging" Remote Sensing 14, no. 16: 4115. https://doi.org/10.3390/rs14164115
APA StyleHuang, F., Lin, P., Cao, R., Zhou, B., & Wu, X. (2022). Dictionary Learning- and Total Variation-Based High-Light-Efficiency Snapshot Multi-Aperture Spectral Imaging. Remote Sensing, 14(16), 4115. https://doi.org/10.3390/rs14164115