Investigating the Effects of Snow Cover and Vegetation on Soil Temperature Using Remote Sensing Indicators in the Three River Source Region, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
2.2. Data
2.2.1. Site Data
2.2.2. Reanalysis Data
2.2.3. Remote Sensing Data
2.2.4. Auxiliary Data
2.3. Method
2.3.1. Model Evaluation
2.3.2. Correlation Analysis
2.3.3. Trend Analysis
2.3.4. Regression Method
2.3.5. Data Pre-Processing
3. Results
3.1. Models Selection
3.2. Result Validation
3.3. Results Analysis
3.3.1. Interannual Variation
3.3.2. Seasonal Changes
- (1)
- Regional Average
- (2)
- Spatial Distribution
4. Discussion
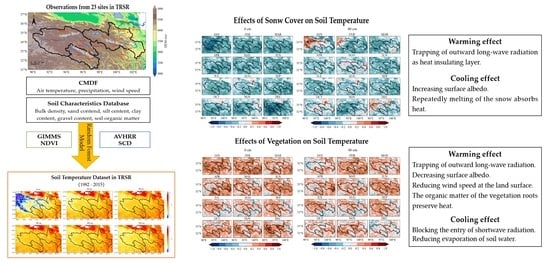
4.1. Soil Temperature in Correlation with Snow Cover
4.2. Soil Temperature in Correlation with Vegetation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, L.; Li, L.; Liu, C.; Cuo, L. Climate Change in the Tibetan Plateau Three Rivers Source Region: 1960–2009. Int. J. Climatol. 2013, 33, 2900–2916. [Google Scholar] [CrossRef]
- Bai, Y.; Guo, C.; Degen, A.A.; Ahmad, A.A.; Wang, W.; Zhang, T.; Li, W.; Ma, L.; Huang, M.; Zeng, H. Climate Warming Benefits Alpine Vegetation Growth in Three-River Headwater Region. China Sci. Total Environ. 2020, 742, 140574. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; You, Q.; Wu, F.; Sun, B.; Cai, Z. Changes of climate and climate extremes in the Three-Rivers Headwaters’ Region over the Tibetan Plateau during the past 60 years. Trans. Atmos. Sci. 2020, 43, 1042–1055. (In Chinese) [Google Scholar]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y. The Impacts of Climate Change on Water Resources and Agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Yan, L.; Wen, T.; Feng, X. Characteristics of Climate Change and Its Impact Assessment in the Three-River Regions. Plateau Meteorol. 2022, 41, 306–316. (In Chinese) [Google Scholar]
- Luo, S.; Fang, X.; Lyu, S.; Ma, D.; Chang, Y.; Song, M.; Chen, H. Frozen Ground Temperature Trends Associated with Climate Change in the Tibetan Plateau Three River Source Region from 1980 to 2014. Clim. Res. 2016, 67, 241–255. [Google Scholar] [CrossRef] [Green Version]
- Cheng, G.; Zhao, L.; Li, R.; Wu, X.; Sheng, Y.; Hu, G.; Zou, D.; Jin, H.; Li, X.; Wu, Q. Characteristic, changes and impacts of permafrost on Qinghai-Tibet Plateau. Chin. Sci. Bull. 2019, 64, 2783–2795. (In Chinese) [Google Scholar]
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Wu, J.; Xie, C.; Wu, X.; Pang, Q.; et al. A New Map of Permafrost Distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Yang, D.; Fang, B.; Yang, W.; Qin, Y.; Wang, Y. Data-Driven Mapping of the Spatial Distribution and Potential Changes of Frozen Ground over the Tibetan Plateau. Sci. Total Environ. 2019, 649, 515–525. [Google Scholar] [CrossRef]
- Luo, S.; Wang, J.; Pomeroy, J.W.; Lyu, S. Freeze–Thaw Changes of Seasonally Frozen Ground on the Tibetan Plateau from 1960 to 2014. J. Clim. 2020, 33, 9427–9446. [Google Scholar] [CrossRef]
- Deluigi, N.; Lambiel, C.; Kanevski, M. Data-Driven Mapping of the Potential Mountain Permafrost Distribution. Sci. Total Environ. 2017, 590–591, 370–380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, S.; Wu, Q.; Zhang, Z.; Xu, X. Impact of Climatic Factors on Permafrost of the Qinghai–Xizang Plateau in the Time-Frequency. Domain Quat. Int. 2015, 374, 110–117. [Google Scholar] [CrossRef]
- Xing, L.; Li, L.; Gong, J.; Ren, C.; Liu, J.; Chen, H. Daily Soil Temperatures Predictions for Various Climates in United States Using Data-Driven Model. Energy 2018, 160, 430–440. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G.; Nan, Z.; Che, J.; Sheng, Y.; Wu, Q.; Jin, H.; Luo, D.; Tang, Z.; et al. Mapping the Permafrost Stability on the Tibetan Plateau for 2005–2015. Sci. China Earth Sci. 2020, 64, 62–79. [Google Scholar] [CrossRef]
- Jin, H.; Sun, K.; Wang, S.; He, R.; Lv, L.; Yu, S. Dual Influences of Local Environmental Variables on Ground Temperatures on the Interior-Eastern Qingha-i Tibet Plateau (Ⅰ): Vegetation and Snow Cover. J. Glaciol. Geocryol. 2008, 30, 535–545. (In Chinese) [Google Scholar]
- Smith, M.W. Microclimatic Influences on Ground Temperatures and Permafrost Distribution, Mackenzie Delta, Northwest Territories. Can. J. Earth Sci. 1975, 12, 1421–1438. [Google Scholar] [CrossRef]
- Ni, J.; Cheng, Y.; Wang, Q.; Ng, C.W.W.; Garg, A. Effects of Vegetation on Soil Temperature and Water Content: Field Monitoring and Numerical Modelling. J. Hydrol. 2019, 571, 494–502. [Google Scholar] [CrossRef]
- Flanner, M.G.; Shell, K.M.; Barlage, M.; Perovich, D.K.; Tschudi, M. Radiative Forcing and Albedo Feedback from the Northern Hemisphere Cryosphere between 1979 and 2008. Nat. Geosci. 2011, 4, 151–155. [Google Scholar] [CrossRef]
- Li, W.; Luo, S.; Hao, X.; Wang, J.; Wang, Y. Observations of East Qinghai-Xizang Plateau Snow Cover Effects on Surface Energy and Water Exchange in Different Seasons. Plateau Meteorol. 2021, 40, 455–471. (In Chinese) [Google Scholar]
- Fu, Q.; Hou, R.; Li, T.; Wang, M.; Yan, J. The Functions of Soil Water and Heat Transfer to the Environment and Associated Response Mechanisms under Different Snow Cover Conditions. Geoderma 2018, 325, 9–17. [Google Scholar] [CrossRef]
- Zhang, T. Influence of the Seasonal Snow Cover on the Ground Thermal Regime: An Overview. Rev. Geophys. 2005, 43, RG4002. [Google Scholar] [CrossRef]
- Qian, B.; Gregorich, E.G.; Gameda, S.; Hopkins, D.W.; Wang, X.L. Observed Soil Temperature Trends Associated with Climate Change in Canada. J. Geophys. Res. Atmos. 2011, 116, D02106. [Google Scholar] [CrossRef]
- Aalto, J.; le Roux, P.C.; Luoto, M. Vegetation Mediates Soil Temperature and Moisture in Arctic-Alpine Environments. Arct. Antarct. Alp. Res. 2018, 45, 429–439. [Google Scholar] [CrossRef] [Green Version]
- Feng, H.; Ye, S.; Zou, B. Contribution of Vegetation Change to the Surface Radiation Budget: A Satellite Perspective. Glob. Planet. Change 2020, 192, 103225. [Google Scholar] [CrossRef]
- Lu, Y.; Yu, W.; Guo, M.; Liu, W. Spatiotemporal variation characteristics of land cover and land surface temperature in Mohe County, Helongjiang Province. J. Glaciol. Geocryol. 2017, 39, 1137–1149. (In Chinese) [Google Scholar]
- Way, R.G.; Lapalme, C.M. Does Tall Vegetation Warm or Cool the Ground Surface? Constraining the Ground Thermal Impacts of Upright Vegetation in Northern Environments. Environ. Res. Lett. 2021, 16, 054077. [Google Scholar] [CrossRef]
- Chang, X.; Jin, H.; Wang, Y.; Zhang, Y.; Zhou, G.; Che, F.; Zhao, Y. Influences of vegetation on permafrost: A review. Acta Ecol. Sin. 2012, 32, 7981–7990. (In Chinese) [Google Scholar] [CrossRef] [Green Version]
- Luo, D.; Jin, H.; He, R.; Yang, S. Responses of Surface Vegetation on Soil Temperature and Moisture of the Active Layer in the Source Area of the Yellow River. J. Earth Sci. J. China Univ. Geosci. 2014, 39, 421–430. (In Chinese) [Google Scholar]
- Song, Y.; Zhou, D.; Zhang, H.; Li, G.; Jin, Y.; Li, Q. Effects of Vegetation Height and Density on Soil Temperature Variations. Chin. Sci. Bull. 2013, 58, 907–912. [Google Scholar] [CrossRef] [Green Version]
- Kun, Y.; Jie, H.; China Meteorological Forcing Dataset (1979–2018). A Big Earth Data Platf. Three Poles 2019. Available online: http://data.tpdc.ac.cn/en/data/8028b944-daaa-4511-8769-965612652c49/ (accessed on 19 July 2022).
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C. On Downward Shortwave and Longwave Radiations over High Altitude Regions: Observation and Modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The First High-Resolution Meteorological Forcing Dataset for Land. Process Stud. Over China Sci. Data 2020, 7, 1–11. [Google Scholar]
- Hao, X.; Huang, G.; Che, T.; Ji, W.; Sun, X.; Zhao, Q.; Zhao, H.; Wang, J.; Li, H.; Yang, Q. The Nieer Avhrr Snow Cover Extent Product over China–a Long-Term Daily Snow Record for Regional Climate Research. Earth Syst. Sci. Data 2021, 13, 4711–4726. [Google Scholar] [CrossRef]
- Wu, D.; Wu, H.; Zhao, X.; Zhou, T.; Tang, B.; Zhao, W.; Jia, K. Evaluation of Spatiotemporal Variations of Global Fractional Vegetation Cover Based on Gimms Ndvi Data from 1982 to 2011. Remote Sens. 2014, 6, 4217–4239. [Google Scholar] [CrossRef] [Green Version]
- Shangguan, W.; Dai, Y.; Liu, B.; Zhu, A.; Duan, Q.; Wu, L.; Ji, D.; Ye, A.; Yuan, H.; Zhang, Q. A China Data Set of Soil Properties for Land Surface Modeling Journal of Advances in Modeling. Earth Syst. 2013, 5, 212–224. [Google Scholar]
- Hamed, K.H.; Rao, A.R. A Modified Mann-Kendall Trend Test for Autocorrelated Data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Deluigi, N.; Lambiel, C. Permal: A Machine Learning Approach for Alpine Permafrost Distribution Modeling; Eidg. Forschungsanstalt WSL: Zürcherstrasse, Switzerland, 2013. [Google Scholar]
- Gunn, S.R. Support Vector Machines for Classification and Regression. ISIS Tech. Rep. 1998, 14, 5–16. [Google Scholar]
- Vapnik, V.N. An Overview of Statistical Learning Theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Hutengs, C.; Vohland, M. Downscaling Land Surface Temperatures at Regional Scales with Random Forest Regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Wang, J.; Luo, S.; Li, Z.; Wang, S.; Li, Z. The Freeze/Thaw Process and the Surface Energy Budget of the Seasonally Frozen Ground in the Source Region of the Yellow River. Theor. Appl. Climatol. 2019, 138, 1631–1646. [Google Scholar] [CrossRef] [Green Version]
- Hussain, M.M.; Mahmud, I. Pymannkendall: A Python Package for Non Parametric Mann Kendall Family of Trend. Tests J. Open Source Softw. 2019, 4, 1556. [Google Scholar] [CrossRef]
- Luo, S.; Li, H.; Ma, D.; Li, W.; Wang, J.; Tan, X.; Dong, Q. Review and Prospects of Frozen Soil-Vegetation Interaction and Climate Effects in the Three Rivers Source Region. Plateau Meteorol. 2022, 41, 255–267. (In Chinese) [Google Scholar]













| R2 | RMSE (°C) | Bias (°C) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MLR | SVM | RF | MLR | SVM | RF | MLR | SVM | RF | |
| 0 cm | 0.9868 | 0.9578 | 0.9913 | 1.1709 | 2.0741 | 0.9581 | 0.0250 | −0.1726 | 0.0168 |
| 5 cm | 0.9841 | 0.9720 | 0.9935 | 1.1171 | 1.4871 | 0.7172 | −0.0676 | −0.1495 | −0.0524 |
| 10 cm | 0.9821 | 0.9727 | 0.9933 | 1.1451 | 1.4171 | 0.7032 | −0.0550 | −0.1138 | −0.0369 |
| 15 cm | 0.9811 | 0.9727 | 0.9931 | 1.1557 | 1.4005 | 0.6974 | −0.0621 | −0.1150 | −0.0320 |
| 20 cm | 0.9779 | 0.9720 | 0.9926 | 1.2055 | 1.3584 | 0.7063 | −0.0630 | −0.1140 | −0.0181 |
| 40 cm | 0.9495 | 0.9588 | 0.9862 | 1.6590 | 1.4804 | 0.8570 | −0.0520 | −0.1250 | 0.0102 |
| 80 cm | 0.9289 | 0.9437 | 0.9811 | 1.6037 | 1.4326 | 0.8267 | −0.1547 | −0.1561 | −0.0433 |
| 160 cm | 0.8786 | 0.9517 | 0.9769 | 1.6367 | 1.0303 | 0.7104 | −0.0813 | −0.0401 | −0.0446 |
| 320 cm | 0.8542 | 0.9400 | 0.9735 | 1.3420 | 0.8527 | 0.5704 | −0.0472 | −0.0283 | −0.0275 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, X.; Luo, S.; Li, H.; Hao, X.; Wang, J.; Dong, Q.; Chen, Z. Investigating the Effects of Snow Cover and Vegetation on Soil Temperature Using Remote Sensing Indicators in the Three River Source Region, China. Remote Sens. 2022, 14, 4114. https://doi.org/10.3390/rs14164114
Tan X, Luo S, Li H, Hao X, Wang J, Dong Q, Chen Z. Investigating the Effects of Snow Cover and Vegetation on Soil Temperature Using Remote Sensing Indicators in the Three River Source Region, China. Remote Sensing. 2022; 14(16):4114. https://doi.org/10.3390/rs14164114
Chicago/Turabian StyleTan, Xiaoqing, Siqiong Luo, Hongmei Li, Xiaohua Hao, Jingyuan Wang, Qingxue Dong, and Zihang Chen. 2022. "Investigating the Effects of Snow Cover and Vegetation on Soil Temperature Using Remote Sensing Indicators in the Three River Source Region, China" Remote Sensing 14, no. 16: 4114. https://doi.org/10.3390/rs14164114
APA StyleTan, X., Luo, S., Li, H., Hao, X., Wang, J., Dong, Q., & Chen, Z. (2022). Investigating the Effects of Snow Cover and Vegetation on Soil Temperature Using Remote Sensing Indicators in the Three River Source Region, China. Remote Sensing, 14(16), 4114. https://doi.org/10.3390/rs14164114