1. Introduction
Most existing radars are single-polarization array radars, such as MIMO radar, which can only receive one type of polarization information [
1,
2,
3] of the electromagnetic wave signal. The vector sensor radar, namely the polarization radar, has polarization diversity characteristics and can obtain at least two types of polarization information or up to six types of polarization information [
4,
5,
6,
7,
8,
9,
10] of the electromagnetic wave signal. Refs. [
4,
5,
6,
7] studied the angle estimation of the specially separated electromagnetic vector sensor array, and showed that the polarization information can improve the performance of angle estimation.
Refs. [
8,
9,
10] studied the array popularity of large electric dipoles and magnetic loops and proposed corresponding angle and polarization estimation algorithms. It is well known that direction of arrival (DOA) estimation is an important part of array signal processing [
11,
12], in particular the height measurement of low altitude targets, which is affected by multipath and is difficult to measure accurately [
13,
14,
15,
16,
17,
18]. Severe multipath coherence signals exist in the low-elevation areas, which seriously affects the height measurement accuracy.
Therefore, polarimetric MIMO radar with both spatial diversity and polarization diversity has attracted the attention of many scholars [
19,
20,
21,
22]. In order to make full use of the advantages of polarimetric MIMO radar, Ref. [
23] proposed a polarized smoothing generalized multiple signal classification (MUSIC) algorithm based on the generalized MUSIC algorithm, which improved the height measurement accuracy. Based on the MUSIC algorithm [
24], Zheng [
25] proposed the steering vector synthesis MUSIC algorithm and generalized MUSIC algorithms for the meter-wave polarimetric MIMO radar, which take full advantage of the waveform diversity and polarization diversity with good estimation accuracy and without decoherence processing.
The paper proposes the idea of matrix reconstruction as well as the operation of real-value processing to further improve the estimation accuracy and reduce the computational complexity. The work is motivated to improve the angle estimation accuracy with reduced computational complexity. The problem of the existing algorithms is that the improvement of the angle measurement accuracy and the amount of calculations are contradictory and cannot be unified. The challenges of the topic are to better apply and combine these technologies.
In order to make better use of the advantages of polarimetric MIMO radar, we first analyze the signal model of meter wave polarimetric MIMO radar in the low-elevation area and then study a method based on matrix reconstruction without any prior information. By taking full advantage of the waveform diversity and polarization diversity advantages of the polarimetric MIMO radar, the proposed method has good accuracy at the case of low snapshots or a low signal-to-noise ratio (SNR).
Finally, the proposed algorithm is further analyzed through computer simulation results, and then the correctness and advantages of the proposed algorithm are verified after comparison with the existing algorithms. The innovation of this paper is to apply the polarization MIMO radar to the height measurement of complex terrain. The matrix reconstruction in this paper does not require the prior information of the terrain, and the real value technology can improve the accuracy of height measurement and reduce the amount of calculation.
Notations: Superscript , and denote conjugate, transpose and conjugate transpose, respectively. denotes Kronecker product, respectively. is an identity matrix with dimension . is the exchange matrix with ones on its anti-diagonal and zeros elsewhere. denotes the matrix determinant.
2. Signal Model of Meter Wave Polarimetric MIMO Radar in Low Elevation Area
The schematic diagram of the polarimetric MIMO radar is shown in
Figure 1. The transceiver antennas are all vertically placed with polarization sensitive antenna, and its adjust sensor spacing equals
, where
is the wavelength.
is the direct wave angle,
is the reflection angle,
is the height of the array, and
is the height of the target.
There are
vector sensors in the polarimetric MIMO radar. The transmitted signals of polarimetric MIMO radar are assumed to be a set of orthogonal signals
, where
, which satisfies the following Equation (1).
Assuming that the low elevation reflection area is smooth and flat ground, the signal of
th snapshot reaching at the target can be represented as
where
is the phase difference due to the range difference of wave propagation between the direct wave and reflected wave,
is the distance between the projection of the target on the ground and the radar, and
is the Fresnel reflection coefficient of the horizontally polarized wave with a value of
where
is the surface complex dielectric constant, which can be represented by the relative dielectric constant
and the surface material conductivity
:
.
is the whole steering vector, which equals
, where
is the spacial steering vector and
is the polarization steering vector of a single electromagnetic vector sensor, which can be expressed as:
where
represents
or
, and
. Therefore, we can obtain the values of
. As elevation measurement is the primary purpose of this paper, we set the azimuth as
. Data for the
th snapshot received by the entire array can be expressed as
where
is the complex reflection coefficient, and
is the Gaussian white noise, with a mean of zero and a variance of
. The following formula can be obtained after matching filtering using the transmitted signals to Equation (6):
For Equation (7), the received data under the
th snapshot can be expressed as the following formula,
According to the conclusion of Ref. [
21], the noise of
is still Gaussian white noise after matching filtering and vectorization operation.
3. Real Valued MUSIC Height Measurement Method Based on Matrix Reconstruction
To solve the problem of the effect of the multi-path reflection echo signal in the low-elevation area of the polarimetric MIMO radar, this section reconstructs the received signal data Equation (8) as matrix
, which can be expressed as the following equation:
where
represents the data received by the
th vector sensor and the
th transmitted signal. Equation (9) can be expanded as the following formula:
where
is the steering vector after the matrix reconstruction,
is the noise matrix of the reconstructed data,
contains all the polarization information of the received data, and
includes the reflection coefficient, the range difference of wave propagation and other information as follows.
After observation, it is not difficult to find that the column of is linear independent and, when , , has rank . Furthermore, it is important to note that, in Equation (10), when the rank of is 4, the rank loss generated by the multipath coherence signal has been resolved, i.e., the matrix reconstruction method eliminates the effect of the multipath coherence signal. With noncoherent low elevation targets, the proposed method can solve the multipath coherent rank loss phenomenon for, at most, .
However, the values in Equation (10) are complex values, and thus direct low-elevation estimation leads to greater computational complexity. To reduce the algorithm complexity, we perform the real-value processing using the unitary matrix with Equation (10) and derive the corresponding real-value MUSIC elevation estimation method.
When the received data has
snapshots, the corresponding data expression of
can be obtained by Equation (10). To make full use of the conjugated data,
can be extended as
where
is a commutative matrix with 1 on the antidiagonal elements and the remaining position elements of 0. We can easily verify that
is the centrosymmetric Hermite matrix [
26], and the real-valued matrix can be obtained by processing with Equation (14) using the unitary matrix [
27].
where
is a sparse unitary matrix, whose odd and even dimensions are defined as, respectively:
When the number of dimension of received data is large, the huge calculation amount will increase the practical application difficulty. In order to reduce the dimension of the receiving data, and to reduce the impact of the noise on the data, we can use Singular Value Decomposition (SVD) technology to handle Equation (15), as follows:
As there are four transmission paths in the low elevation region for one target and the reconstructed data covariance matrix rank is 4; therefore,
and
are composed of left singular value vectors corresponding to four large singular values and left singular values corresponding to
small singular values.
and
consist of four large singular values and the remaining
large singular values. Similarly,
and
consists of right singular value vectors corresponding to four large singular values and a vector of right singular values corresponding to
small singular values. Equation (15) right is multiplied with
, and then we have
According to Equation (18), the dimension of matrix decreases from to 4. It is not difficult to find when the number of snapshots is large, and thus it is not difficult to prove that singular value techniques can greatly reduce the matrix dimension.
In the same way, the covariance matrix of the real-valued data can be obtained by the following equation:
Eigenvalue decomposition of matrix
yields the following formula.
Matrices
and
represent the signal and noise subspaces, respectively, whose eigenvalues constitute the diagonal matrices
and
. Since
is a real-valued matrix, both
and
are real-valued matrices. Based on the orthogonality of the signal subspace and noise subspace, the following spectrum formula can be obtained.
Equation (21) is called the generalized MUSIC algorithm. The difference between it and the traditional MUSIC algorithm is that there is no need for information of the steering vector. It is sufficient to know the steering matrix because the steering matrix is orthogonal to the noise subspace and because the angle estimation can be obtained by using this point.
As the received data is processed as real-valued data by the unitary matrix, the steering vector for the spectral peak search in Equation (21) does not contain any polarization parameter, the range difference of wave propagation and reflection coefficient information; thus, it is not difficult to prove that the proposed method can estimate the target elevation value without the polarization information.
The above equation is a two-dimensional spectral peak search, which can be reduced to a one-dimensional search according to the relationship between the angle of direct wave and the reflected wave as shown below
Based on the distance
R and elevation estimations, the height of the target can be calculated as:
4. Summary and Computational Complexity of the Proposed Algorithm
The algorithm steps studied in this paper are as follows:
Reconstruct the received signal data using Equation (9).
The unitary matrix is used to process the real-value of the reconstructed received signal matrix.
Reduce the effect of big dimension of received data and noise using the singular value technique.
The signal covariance matrix was obtained by Equation (19), and then the eigenvalue was decomposed to obtain the noise subspace matrix.
According to the noise subspace matrix, the spectral peak search was performed as in Equation (21).
The target height is obtained according to the geometric relationship of Equation (23).
According to the algorithm steps, it is not difficult to find that the complexity of the proposed method is mainly divided into the following parts: (1) real-valued processing; (2) estimate the real-valued covariance matrix; (3) eigenvalue decomposition of the covariance; and (4) spectral peak search. The specific expression is as follows: (1) ; (2) ; (3) ; (4) . Therefore, the complexity of the proposed algorithm is .
The generalized MUSIC algorithm proposed in Ref. [
28] is abbreviated as G-MUSIC; the generalized MUSIC algorithm applied in polarimetric MIMO radar is abbreviated as PG-MUSIC [
23]; the height measurement method of maximum likelihood estimation proposed in Ref. [
29] is abbreviated as the ML algorithm; and its extension algorithm in polarimetric MIMO radar is abbreviated as P-ML [
25]. The G-MUSIC algorithm complexity is
.
The complexity of PG-MUSIC algorithm is . The complexity of ML algorithm is . The complexity of P-ML algorithm is .
5. Computer Simulation Results
This section verifies the reliability and superiority of the proposed algorithm mainly through simulation experiments. In this paper, the angle search range is set as
, the search angle interval is
, and the number of searches is
. A meter-wave polarimetric MIMO radar system has the transceiver array elements
, and the adjusted element spacing is
. In addition, the wavelength is set as
. The height array is
, and number of Monte Carlo experiments is
. In simulation experiments, the number of target is set to 1, and the root mean square error is defined as
where
is the estimated elevation value obtained by the
th experiment,
is the estimated target height obtained by the
th experiment, and
is the number of Monte Carlo experiments.
Example 1: In this experiment, the number of
, the actual elevation of the target is
. The SNR is set as 10 dB.
Figure 2 is a spatial spectrum of the proposed method with 10 times. It can be seen from
Figure 2 that the proposed method can correctly measure the target elevation angle, which proves the correctness of the proposed method.
Example 2: In this experiment, the number of snapshots is
, the actual elevation of the target is
, the distance between the target and the radar is R = 200 km, and the range of SNR is from −10 to 10 dB.
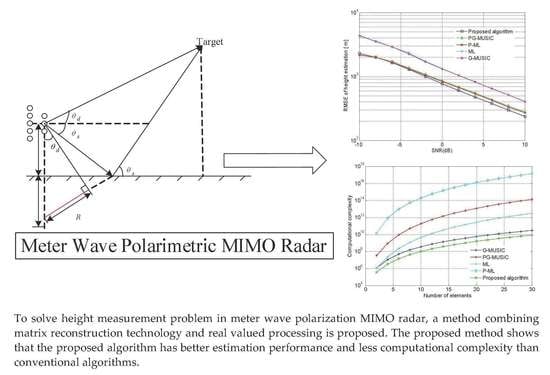
Figure 3 shows the relationship between the RMSE of angle estimation and SNR for the five algorithms, and
Figure 4 shows the RMSR of height measurement and SNR of the five algorithms.
From
Figure 3 and
Figure 4, the PG-MUSIC and P-ML methods show better estimation accuracy than the G-MUSIC and ML methods, which demonstrates the polarization diversity advantage of polarizing-sensitive arrays. Moreover, the proposed algorithm outperforms the PG-MUSIC and P-ML methods, which demonstrates the superiority of the proposed algorithm.
Example 3:
Figure 5 shows the relationship between the computational complexity and the number of array elements of the five algorithms. It can be found from
Figure 5 that the computational complexity of the PG-MUSIC and P-ML methods is significantly higher than that for the G-MUSIC and ML methods. This indicates that, although polarimetric MIMO radar has a polarization diversity advantage, it also increases the algorithmic computational complexity.
Notably, the proposed algorithm has the lowest computational complexity because of the data with real values and because the steering vector dimension for spectrum search is lower than for the PG-MUSIC and P-ML methods. This proves that the proposed method is more conducive to engineering implementations. In addition, according to the experimental results of this example and example 2, compared with the other four algorithms, the proposed algorithm reduces the computing complexity and improves the accuracy of the target elevation and height measurement.
6. Conclusions
To further improve the measurement accuracy, we studied a height measurement method based on the meter-wave polarimetric MIMO radar, which makes full use of the waveform diversity and polarization diversity. First, the receiving signal model was analyzed. According to the height measurement signal model, the received data matrix was reconstructed to eliminate the effect of the multipath reflection echo. To reduce the algorithm complexity, the reconstructed data matrix was processed with real values using a unitary matrix.
Finally, the corresponding spectrum search was presented, which requires no known polarization information. In the simulation experiment, the proposed algorithm was comprehensively compared with the state-of-the-art algorithms, which showed that the proposed algorithm had the best performance. Therefore, when selecting the estimation algorithms, we can consider using the real value processing technology in this paper to improve the diversity of samples. In addition, the decoherence method of matrix reconstruction is a good decoherence method that does not depend on the information of the terrain.