Fine-Grained Classification of Optical Remote Sensing Ship Images Based on Deep Convolution Neural Network
Abstract
:1. Introduction
- Intra-class difference. Ships of the same kind differ in the layout of their deck superstructure.
- Inter-class similarity. Different categories of ships may also have some similar features.
- Long-tailed distribution. The number of each category in the dataset is seriously unbalanced.
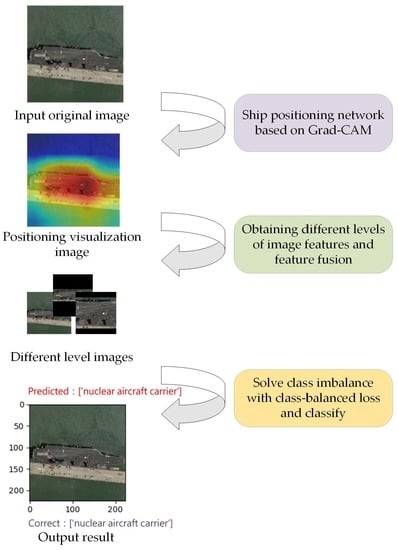
- Gradient-weighted class activation mapping (Grad-CAM) is used to locate the ship position from the images and obtain the midship area with rich information. Then, the categories of the ship are finely recognized by fusing the global and local features of the image.
- By adding self-calibrated convolutions (SC-conv) [13] to the classification network, different contextual information is collected to expand the field of vision and enrich the output features.
- By introducing the class-balanced loss (CB loss), the samples are re-weighted to solve the long-tail distribution problem of the remote sensing ship image dataset.
2. Related Work
3. Materials and Methods
| Algorithm 1. The recognition process of fine-grained optical remote sensing ships. |
| Input: The original image . 1 Obtaining class activation maps by Grad-CAM. 2 for each original image in the dataset do 3 Get the ship target-level image and key part image are obtained by threshold segmentation; 4 Take SC-conv to obtain the features of the three-level input images, respectively; 5 Fusion of feature vectors; 6 Using CB loss to reduce the error caused by the long-tailed distribution of the dataset; Output: Classification results. |
3.1. Target Location Based on Grad-CAM
3.2. Self-Calibrated Convolutions
3.3. Class-Balanced Loss
4. Experiments and Discussion
4.1. Dataset and Image Processing
4.1.1. Dataset
4.1.2. Image Processing
4.2. Implementation Details
4.3. Visualization of Results
4.3.1. Feature Visualization
4.3.2. CM and Recall Rate
4.3.3. Display of Classification Results
4.4. Ablation Experiment
4.5. Long-Tailed Distribution Experiment
4.6. Compared with Other State-of-the-Art Methods
4.7. Robustness Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Lv, Y.; Yao, L.; Xiong, W.; Fu, C. A New Benchmark and an Attribute-Guided Multilevel Feature Representation Network for Fine-Grained Ship Classification in Optical Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1271–1285. [Google Scholar] [CrossRef]
- Antelo, J.; Ambrosio, G.; Gonzalez, J.; Galindo, C. Ship detection and recognitionin high-resolution satellite images. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 12–17 July 2009; pp. IV-514–IV-517. [Google Scholar]
- Selvi, M.U.; Kumar, S.S. A Novel Approach for Ship Recognition Using Shape and Texture. Int. J. Adv. Inf. Technol. (IJAIT) 2011, 1. [Google Scholar] [CrossRef]
- Leng, X.; Ji, K.; Zhou, S.; Xing, X.; Zou, H. A comb feature for the analysis of ship classification in high resolution SAR imagery. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–4. [Google Scholar]
- Wang, Q.; Gao, X.; Chen, D. Pattern Recognition for Ship Based on Bayesian Networks. In Proceedings of the Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007), Haikou, China, 24–27 August 2007; pp. 684–688. [Google Scholar]
- Lang, H.; Wu, S.; Xu, Y. Ship Classification in SAR Images Improved by AIS Knowledge Transfer. IEEE Geosci. Remote Sens. Lett. 2018, 15, 439–443. [Google Scholar] [CrossRef]
- Chen, J.; Qian, Y. Hierarchical Multilabel Ship Classification in Remote Sensing Images Using Label Relation Graphs. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5611513. [Google Scholar] [CrossRef]
- Shi, Q.; Li, W.; Tao, R. 2D-DFrFT Based Deep Network for Ship Classification in Remote Sensing Imagery. In Proceedings of the 2018 10th IAPR Workshop on Pattern Recognition in Remote Sensing (PRRS), Beijing, China, 19–20 August 2018; pp. 1–5. [Google Scholar]
- Liu, K.; Yu, S.; Liu, S. An Improved InceptionV3 Network for Obscured Ship Classification in Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens 2020, 13, 4738–4747. [Google Scholar] [CrossRef]
- Chen, J.; Chen, K.; Chen, H.; Li, W.; Zou, Z.; Shi, Z. Contrastive Learning for Fine-Grained Ship Classification in Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4707916. [Google Scholar] [CrossRef]
- Xiong, W.; Xiong, Z.; Cui, Y. An Explainable Attention Network for Fine-Grained Ship Classification Using Remote-Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5620314. [Google Scholar] [CrossRef]
- Hu, T.; Qi, H. See Better Before Looking Closer: Weakly Supervised Data Augmentation Network for Fine-Grained Visual Classification. arXiv 2019, arXiv:1901.09891. [Google Scholar]
- Liu, J.J.; Hou, Q.; Cheng, M.M.; Wang, C.; Feng, J. Improving Convolutional Networks with Self-Calibrated Convolutions. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 10093–10102. [Google Scholar]
- Zhang, N.; Donahu, J.; Girshick, R.; Darrell, T. Part-based R-CNNs for fine-grained category detection. In Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Volume 8689, pp. 834–849. [Google Scholar]
- Branson, S.; Horn, G.V.; Belongie, S.; Perona, P. Bird species categorization using pose normalized deep convolutional nets. arXiv 2014, arXiv:1406.2952. [Google Scholar]
- Xiao, T.; Xu, Y.; Yang, K.; Zhang, J.; Peng, Y.; Zhang, Z. The application of two-level attention models in deep convolutional neural network for fine-grained image classification. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 842–850. [Google Scholar]
- Zheng, H.; Fu, J.; Mei, T.; Luo, J. Learning Multi-attention Convolutional Neural Network for Fine-Grained Image Recognition. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5219–5227. [Google Scholar]
- Wang, Y.; Morariu, V.I.; Davis, L.S. Learning a Discriminative Filter Bank Within a CNN for Fine-Grained Recognition. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4148–4157. [Google Scholar]
- Chen, Y.; Bai, Y.; Zhang, W.; Mei, T. Destruction and Construction Learning for Fine-Grained Image Recognition. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5152–5161. [Google Scholar]
- Yu, C.; Zha, X.; Zheng, Q.; Zhang, P.; You, X. Hierarchical Bilinear Pooling for Fine-Grained Visual Recognition. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Volume 11220, pp. 595–610. [Google Scholar]
- Kong, S.; Fowlkes, C. Low-Rank Bilinear Pooling for Fine-Grained Classification. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 7025–7034. [Google Scholar]
- Fu, J.; Zheng, H.; Mei, T. Look Closer to See Better: Recurrent Attention Convolutional Neural Network for Fine-Grained Image Recognition. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4476–4484. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Wang, Y.; Gan, W.; Yang, J.; Wu, W.; Yan, J. Dynamic Curriculum Learning for Imbalanced Data Classification. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 5016–5025. [Google Scholar]
- Cui, Y.; Jia, M.; Lin, T.; Song, Y.; Belongie, S. Class-Balanced Loss Based on Effective Number of Samples. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9260–9269. [Google Scholar]
- Liu, J.; Sun, Y.; Han, C.; Dou, Z.; Li, W. Deep Representation Learning on Long-Tailed Data: A Learnable Embedding Augmentation Perspective. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 2967–2976. [Google Scholar]
- Liu, Z.; Yuan, L.; Weng, L.; Yang, Y. A High Resolution Optical Satellite Image Dataset for Ship Recognition and Some New Baselines. In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM), Porto, Portugal, 24–26 February 2017; Volume 1, pp. 324–331. [Google Scholar]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Zhou, P.; Guo, L. Multi-class geospatial object detection and geographic image classification based on collection of part detectors. ISPRS-J. Photogramm. Remote Sens. 2014, 98, 119–132. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ohsaki, M.; Wang, P.; Matsuda, K.; Katagiri, S.; Watanabe, H.; Ralescu, A. Confusion-Matrix-Based Kernel Logistic Regression for Imbalanced Data Classification. IEEE Trans. Knowl. Data Eng. 2017, 29, 1806–1819. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 2015 International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Di, Y.; Jiang, Z.; Zhang, H. A Public Dataset for Fine-Grained Ship Classification in Optical Remote Sensing Images. Remote Sens. 2021, 13, 747. [Google Scholar] [CrossRef]















| Class | Example Image | Class | Example Image | Class | Example Image | |||
|---|---|---|---|---|---|---|---|---|
| BC |  |  | CS |  |  | FB |  |  |
| OL |  |  | OT |  |  | YA |  |  |
| AH |  |  | CVN |  |  | CVC |  |  |
| LHA |  |  | DDA |  |  | SS |  |  |
| FFG |  |  | DDG |  |  | CG |  |  |
| Category | BC | CS | FB | OL | OT | YA | AH | CVN |
| Number | 948 | 369 | 525 | 138 | 654 | 240 | 81 | 246 |
| Category | CVC | LHA | DDA | SS | FFG | DDG | CG | Total |
| Number | 81 | 264 | 87 | 372 | 135 | 330 | 120 | 4590 |
| Category | BC | CS | FB | OL | OT | YA | AH | CVN |
| Recall/% | 0.9 | 0.96 | 0.9 | 1 | 0.91 | 0.96 | 1 | 0.98 |
| Category | CVC | LHA | DDA | SS | FFG | DDG | CG | |
| Recall/% | 0.94 | 0.92 | 0.89 | 0.95 | 0.93 | 0.91 | 0.96 |
| DS Rate (r) | 1 | 2 | 3 | 4 |
| Accuracy | 92.48 | 92.70 | 92.70 | 92.81 |
| SC-conv | √ | √ | √ | √ | √ | |
| Target area positioning | √ | √ | √ | √ | √ | |
| Global features | √ | √ | √ | √ | ||
| Target-level features | √ | √ | √ | √ | ||
| Key part features | √ | √ | √ | √ | ||
| Accuracy/% | 90.74 | 86.93 | 91.83 | 91.72 | 90.08 | 92.81 |
| Imbalance Factor | β | Accuracy |
|---|---|---|
| 12 | 0.999 | 92.81 |
| 20 | 0.999 | 89.40 |
| 50 | 0.99 | 83.92 |
| Method | Fine Grained Network | Accuracy/% |
|---|---|---|
| VGG16 | 79.96 | |
| Inception V3 | 80.61 | |
| ResNet50 | 84.42 | |
| Bilinear CNN | √ | 88.76 |
| RA-CNN | √ | 88.01 |
| MA-CNN | √ | 89.22 |
| WS-DAN | √ | 90.30 |
| Ours (without Reweighting) | √ | 90.63 |
| IICL-CNN | 85.07 | |
| AMEFRN | √ | 91.07 |
| Ours | √ | 92.81 |
| Method | Fine Grained Network | Accuracy/% |
|---|---|---|
| VGG16 | 80.15 | |
| Inception V3 | 82.97 | |
| ResNet50 | 83.65 | |
| Bilinear CNN | √ | 84.48 |
| RA-CNN | √ | 86.47 |
| MA-CNN | √ | 88.60 |
| WS-DAN | √ | 86.06 |
| Ours (without Reweighting) | √ | 90.52 |
| IICL-CNN | 88.87 | |
| AMEFRN | √ | 92.10 |
| Ours | √ | 93.54 |
| Method | Fine Grained Network | Accuracy/% |
|---|---|---|
| VGG16 | 84.21 | |
| Inception V3 | 86.20 | |
| ResNet50 | 84.66 | |
| Bilinear CNN | √ | 90.50 |
| RA-CNN | √ | 90.95 |
| MA-CNN | √ | 91.07 |
| WS-DAN | √ | 90.56 |
| Ours (without Reweighting) | √ | 92.17 |
| IICL-CNN | 89.99 | |
| AMEFRN | √ | 93.32 |
| Ours | √ | 93.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhang, Z.; Chen, Z.; Zhang, Y.; Wang, J. Fine-Grained Classification of Optical Remote Sensing Ship Images Based on Deep Convolution Neural Network. Remote Sens. 2022, 14, 4566. https://doi.org/10.3390/rs14184566
Chen Y, Zhang Z, Chen Z, Zhang Y, Wang J. Fine-Grained Classification of Optical Remote Sensing Ship Images Based on Deep Convolution Neural Network. Remote Sensing. 2022; 14(18):4566. https://doi.org/10.3390/rs14184566
Chicago/Turabian StyleChen, Yantong, Zhongling Zhang, Zekun Chen, Yanyan Zhang, and Junsheng Wang. 2022. "Fine-Grained Classification of Optical Remote Sensing Ship Images Based on Deep Convolution Neural Network" Remote Sensing 14, no. 18: 4566. https://doi.org/10.3390/rs14184566
APA StyleChen, Y., Zhang, Z., Chen, Z., Zhang, Y., & Wang, J. (2022). Fine-Grained Classification of Optical Remote Sensing Ship Images Based on Deep Convolution Neural Network. Remote Sensing, 14(18), 4566. https://doi.org/10.3390/rs14184566