Diffusion Model with Detail Complement for Super-Resolution of Remote Sensing
Abstract
:1. Introduction
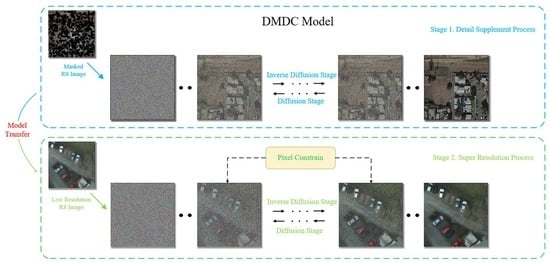
- To the best of our knowledge, we propose a diffusion model with detailed complementary mechanisms for the RSSR task. Different from traditional optimization-based methods, DMDC adopts generation-based methods to enrich image semantics.
- Aiming at the small and dense characteristics of objects in low-resolution RS images, we propose a detail supplementation task for RSSR for the diffusion model, which achieves accurate detail reconstruction for RSSR tasks.
- To reduce the diversity of DMDC, which may not be suitable for super-resolution tasks, we propose a pixel constraint loss to constrain the inverse diffusion process of the diffusion model.
2. Related Work
2.1. Remote Sensing Super Resolution
2.2. Diffusion Model
3. Methodology
3.1. Super Resolution Based Diffusion Model
3.2. Optimizing Diffusion with Detail Complement
3.3. Pixel Constraint Loss
| Algorithm 1 Training a DMDC model |
| 1: Input: , |
| , |
| 2: repeat; |
| 3: Train diffusion model for detail supplement |
| 4: Take a gradient descent step on |
| 5: until converged |
| 6: return: |
| Algorithm 2 Inference in T iterative refinement steps |
| 1: Input: |
| 2: for do |
| 3: if , else |
| 4: |
| 5: |
| 6: end for |
| 7: return |
4. Results and Analysis
4.1. Data Set and Evaluation Metrics
4.1.1. Data Set
4.1.2. Evaluation Metrics
4.2. Implementation Details
4.3. Generate Visualization
4.3.1. Detail Supplement Visualization
4.3.2. Visualization on Potsdam
4.3.3. Visualization on Vaihingen
4.4. Effective of Pixel Constraint Loss
4.5. Comparison with State-of-the-Art
4.6. Discussion of DMDC on PSNR Indicator
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, R.; Zhang, L.; Fu, H. RRSGAN: Reference-based super-resolution for remote sensing image. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–17. [Google Scholar] [CrossRef]
- Zhang, X.g. A new kind of super-resolution reconstruction algorithm based on the ICM and the bicubic interpolation. In Proceedings of the 2008 International Symposium on Intelligent Information Technology Application Workshops, Shanghai, China, 21–22 December 2008; pp. 817–820. [Google Scholar]
- Zhang, X.g. A new kind of super-resolution reconstruction algorithm based on the ICM and the bilinear interpolation. In Proceedings of the 2008 International Seminar on Future BioMedical Information Engineering, Wuhan, China, 18 December 2008; pp. 183–186. [Google Scholar]
- Begin, I.; Ferrie, F. Blind super-resolution using a learning-based approach. In Proceedings of the ICPR 2004: 17th International Conference on Pattern Recognition, Cambridge, UK, 26 August 2004; Volume 2, pp. 85–89. [Google Scholar]
- Joshi, M.V.; Chaudhuri, S.; Panuganti, R. A learning-based method for image super-resolution from zoomed observations. IEEE Trans. Syst. Man Cybern. Part B 2005, 35, 527–537. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.M.; Zhang, J. An improved super-resolution with manifold learning and histogram matching. In International Conference on Biometrics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 756–762. [Google Scholar]
- Ran, Q.; Xu, X.; Zhao, S.; Li, W.; Du, Q. Remote sensing images super-resolution with deep convolution networks. Multimed. Tools Appl. 2020, 79, 8985–9001. [Google Scholar] [CrossRef]
- Zhu, Y.; Geiß, C.; So, E. Image super-resolution with dense-sampling residual channel-spatial attention networks for multi-temporal remote sensing image classification. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102543. [Google Scholar] [CrossRef]
- Ibrahim, M.R.; Benavente, R.; Lumbreras, F.; Ponsa, D. 3DRRDB: Super Resolution of Multiple Remote Sensing Images Using 3D Residual in Residual Dense Blocks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 323–332. [Google Scholar]
- Jiang, K.; Wang, Z.; Yi, P.; Wang, G.; Lu, T.; Jiang, J. Edge-enhanced GAN for remote sensing image superresolution. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5799–5812. [Google Scholar] [CrossRef]
- Xiong, Y.; Guo, S.; Chen, J.; Deng, X.; Sun, L.; Zheng, X.; Xu, W. Improved SRGAN for remote sensing image super-resolution across locations and sensors. Remote Sens. 2020, 12, 1263. [Google Scholar] [CrossRef]
- Li, F.; Jia, X.; Fraser, D. Universal HMT based super resolution for remote sensing images. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 333–336. [Google Scholar]
- Zhu, H.; Tang, X.; Xie, J.; Song, W.; Mo, F.; Gao, X. Spatio-temporal super-resolution reconstruction of remote-sensing images based on adaptive multi-scale detail enhancement. Sensors 2018, 18, 498. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 184–199. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Sohl-Dickstein, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In Proceedings of the PMLR: International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2256–2265. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Nichol, A.Q.; Dhariwal, P. Improved denoising diffusion probabilistic models. In Proceedings of the PMLR: International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 8162–8171. [Google Scholar]
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image super-resolution via iterative refinement. arXiv 2021, arXiv:2104.07636. [Google Scholar] [CrossRef]
- Whang, J.; Delbracio, M.; Talebi, H.; Saharia, C.; Dimakis, A.G.; Milanfar, P. Deblurring via stochastic refinement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21 June 2022; pp. 16293–16303. [Google Scholar]
- Wolleb, J.; Sandkühler, R.; Bieder, F.; Valmaggia, P.; Cattin, P.C. Diffusion Models for Implicit Image Segmentation Ensembles. arXiv 2021, arXiv:2112.03145. [Google Scholar]
- Baranchuk, D.; Rubachev, I.; Voynov, A.; Khrulkov, V.; Babenko, A. Label-efficient semantic segmentation with diffusion models. arXiv 2021, arXiv:2112.03126. [Google Scholar]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-based generative modeling through stochastic differential equations. arXiv 2020, arXiv:2011.13456. [Google Scholar]
- Choi, J.; Kim, S.; Jeong, Y.; Gwon, Y.; Yoon, S. Ilvr: Conditioning method for denoising diffusion probabilistic models. arXiv 2021, arXiv:2108.02938. [Google Scholar]
- Rong, X.; Sun, X.; Diao, W.; Wang, P.; Yuan, Z.; Wang, H. Historical Information-Guided Class-Incremental Semantic Segmentation in Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, W.; Li, C.; Pan, Z.; Mao, Y.; Chen, J.; Li, S.; Wang, H.; Sun, X. Learning to Evaluate Performance of Multi-modal Semantic Localization. IEEE Trans. Geosci. Remote Sens. 2022. [Google Scholar] [CrossRef]
- Mao, Y.; Guo, Z.; Lu, X.; Yuan, Z.; Guo, H. Bidirectional Feature Globalization for Few-shot Semantic Segmentation of 3D Point Cloud Scenes. arXiv 2022, arXiv:2208.06671. [Google Scholar]
- Khan, A.; Govil, H.; Taloor, A.K.; Kumar, G. Identification of artificial groundwater recharge sites in parts of Yamuna River basin India based on Remote Sensing and Geographical Information System. Groundw. Sustain. Dev. 2020, 11, 100415. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, W.; Tian, C.; Rong, X.; Zhang, Z.; Wang, H.; Fu, K.; Sun, X. Remote Sensing Cross-Modal Text-Image Retrieval Based on Global and Local Information. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar]
- Yuan, Z.; Zhang, W.; Rong, X.; Li, X.; Chen, J.; Wang, H.; Fu, K.; Sun, X. A lightweight multi-scale crossmodal text-image retrieval method in remote sensing. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–19. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, W.; Fu, K.; Li, X.; Deng, C.; Wang, H.; Sun, X. Exploring a fine-grained multiscale method for cross-modal remote sensing image retrieval. arXiv 2022, arXiv:2204.09868. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 391–407. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Lin, C.H.; Lin, Y.C.; Tang, P.W. ADMM-ADAM: A new inverse imaging framework blending the advantages of convex optimization and deep learning. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Yang, D.; Li, Z.; Xia, Y.; Chen, Z. Remote sensing image super-resolution: Challenges and approaches. In Proceedings of the 2015 IEEE International Conference on Digital Signal Processing (DSP), Singapore, 21–24 July 2015; pp. 196–200. [Google Scholar]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Luo, Z.; Li, Y.; Cheng, S.; Yu, L.; Wu, Q.; Wen, Z.; Fan, H.; Sun, J.; Liu, S. BSRT: Improving Burst Super-Resolution With Swin Transformer and Flow-Guided Deformable Alignment. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, New Orleans, LA, USA, 19–20 June 2022; pp. 998–1008. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11 October 2021; pp. 10012–10022. [Google Scholar]
- Jia, S.; Wang, Z.; Li, Q.; Jia, X.; Xu, M. Multi-Attention Generative Adversarial Network for Remote Sensing Image Super Resolution. IEEE Trans. Geosci. Remote Sens. 2022. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Rakotonirina, N.C.; Rasoanaivo, A. ESRGAN+: Further improving enhanced super-resolution generative adversarial network. In Proceedings of the ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 3637–3641. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-esrgan: Training real-world blind super-resolution with pure synthetic data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11 October 2021; pp. 1905–1914. [Google Scholar]
- Jo, Y.; Yang, S.; Kim, S.J. Investigating loss functions for extreme super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 424–425. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]
- Yang, X.; Shih, S.M.; Fu, Y.; Zhao, X.; Ji, S. Your ViT is Secretly a Hybrid Discriminative-Generative Diffusion Model. arXiv 2022, arXiv:2208.07791. [Google Scholar]
- Ryu, D.; Ye, J.C. Pyramidal Denoising Diffusion Probabilistic Models. arXiv 2022, arXiv:2208.01864. [Google Scholar]
- Nair, N.G.; Mei, K.; Patel, V.M. AT-DDPM: Restoring Faces degraded by Atmospheric Turbulence using Denoising Diffusion Probabilistic Models. arXiv 2022, arXiv:2208.11284. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-Resolution Image Synthesis With Latent Diffusion Models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–20 June 2022; pp. 10684–10695. [Google Scholar]
- Pandey, K.; Mukherjee, A.; Rai, P.; Kumar, A. Diffusevae: Efficient, controllable and high-fidelity generation from low-dimensional latents. arXiv 2022, arXiv:2201.00308. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Kingma, D.P.; Mohamed, S.; Jimenez Rezende, D.; Welling, M. Semi-supervised learning with deep generative models. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
- Zhang, Q.; Yang, G.; Zhang, G. Collaborative network for super-resolution and semantic segmentation of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Sun, X.; Wang, P.; Yan, Z.; Xu, F.; Wang, R.; Diao, W.; Chen, J.; Li, J.; Feng, Y.; Xu, T.; et al. FAIR1M: A benchmark dataset for fine-grained object recognition in high-resolution remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2022, 184, 116–130. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef]
- Li, J.; Fang, F.; Mei, K.; Zhang, G. Multi-scale residual network for image super-resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 517–532. [Google Scholar]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Deep back-projection networks for super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1664–1673. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]









| Dataset | ×8 (Scale) | ×4 (Scale) | ×2 (Scale) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PSNR↑ | SSIM↑ | BRISQUE↓ | PSNR↑ | SSIMred↑ | BRISQUE↓ | PSNR↑ | SSIM↑ | BRISQUE↓ | ||
| Bicubic | Potsdam Testset | 25.68 | 0.6953 | 32.1548 | 28.21 | 0.7625 | 30.1589 | 32.31 | 0.8746 | 28.6751 |
| EDSR [61] | 25.85 | 0.6987 | 27.1245 | 28.32 | 0.7649 | 26.6271 | 32.58 | 0.8789 | 25.3897 | |
| MSRN [58] | 25.48 | 0.7023 | 26.7856 | 28.29 | 0.7713 | 26.6857 | 32.21 | 0.8803 | 25.8921 | |
| DDBPN [59] | 25.52 | 0.7049 | 24.3217 | 27.32 | 0.7725 | 23.8912 | 32.02 | 0.8934 | 24.3259 | |
| RCAN [60] | 25.92 | 0.7056 | 25.6812 | 28.02 | 0.7756 | 24.8934 | 33.14 | 0.9012 | 22.3487 | |
| DDPM [18] | 25.98 | 0.7173 | 23.3415 | 27.86 | 0.7832 | 22.1258 | 32.12 | 0.9074 | 20.3274 | |
| DMDC (ours) | 25.34 | 0.7329 | 22.9012 | 28.12 | 0.7869 | 20.1645 | 32.87 | 0.9123 | 19.5632 | |
| Driectly Transfer | ||||||||||
| Bicubic | Vaihingen Testset | 20.36 | 0.5632 | 28.1567 | 23.21 | 0.7089 | 26.3489 | 27.73 | 0.8324 | 24.8948 |
| EDSR [61] | 22.24 | 0.5806 | 26.3179 | 24.31 | 0.7205 | 23.4986 | 27.96 | 0.8315 | 22.3472 | |
| MSRN [58] | 21.25 | 0.5749 | 25.5741 | 23.98 | 0.7194 | 22.5914 | 27.48 | 0.8417 | 21.8798 | |
| DDBPN [59] | 21.29 | 0.5864 | 25.3287 | 25.12 | 0.721 | 22.5324 | 28.07 | 0.8397 | 21.5714 | |
| RCAN [60] | 22.34 | 0.5876 | 23.5786 | 24.32 | 0.7231 | 21.8649 | 28.13 | 0.8423 | 20.6819 | |
| DDPM [18] | 22.17 | 0.6427 | 17.8547 | 25.02 | 0.7596 | 17.2684 | 27.63 | 0.8869 | 16.6817 | |
| DMDC (ours) | 23.46 | 0.6696 | 16.6959 | 25.79 | 0.7627 | 15.9487 | 28.24 | 0.8975 | 15.3271 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yuan, Z.; Pan, Z.; Fu, Y.; Liu, L.; Lu, B. Diffusion Model with Detail Complement for Super-Resolution of Remote Sensing. Remote Sens. 2022, 14, 4834. https://doi.org/10.3390/rs14194834
Liu J, Yuan Z, Pan Z, Fu Y, Liu L, Lu B. Diffusion Model with Detail Complement for Super-Resolution of Remote Sensing. Remote Sensing. 2022; 14(19):4834. https://doi.org/10.3390/rs14194834
Chicago/Turabian StyleLiu, Jinzhe, Zhiqiang Yuan, Zhaoying Pan, Yiqun Fu, Li Liu, and Bin Lu. 2022. "Diffusion Model with Detail Complement for Super-Resolution of Remote Sensing" Remote Sensing 14, no. 19: 4834. https://doi.org/10.3390/rs14194834
APA StyleLiu, J., Yuan, Z., Pan, Z., Fu, Y., Liu, L., & Lu, B. (2022). Diffusion Model with Detail Complement for Super-Resolution of Remote Sensing. Remote Sensing, 14(19), 4834. https://doi.org/10.3390/rs14194834