MANet: A Network Architecture for Remote Sensing Spatiotemporal Fusion Based on Multiscale and Attention Mechanisms

Abstract

Obtaining high-spatial–high-temporal (HTHS) resolution remote sensing images from a single sensor remains a great challenge due to the cost and technical limitations. Spatiotemporal fusion (STF) technology breaks through the technical limitations of existing sensors and provides a convenient and economical solution for obtaining HTHS resolution images. At present, most STF methods use stacked convolutional layers to extract image features and then obtain fusion images by using a summation strategy. However, these convolution operations may lead to the loss of feature information, and the summation strategy results in poorly fused images due to a lack of consideration of global spatial feature information. To address these issues, this article proposes a STF network architecture based on multiscale and attention mechanisms (MANet). The multiscale mechanism module composed of dilated convolutions is used to extract the detailed features of low-spatial resolution remote sensing images at multiple scales. The channel attention mechanism adaptively adjusts the weights of the feature map channels to retain more temporal and spatial information in the upsampling process, while the non-local attention mechanism adjusts the initial fusion images to obtain more accurate predicted images by calculating the correlation between pixels. We use two datasets with different characteristics to conduct the experiments, and the results prove that the proposed MANet method with fewer parameters obtains better fusion results than the existing machine learning-based and deep learning-based fusion methods.

1. Introduction

HTHS resolution remote sensing images are significant for remote sensing application fields such as urban land cover mapping [1], disaster warning [2], surface change detection [3], assessment of the area affected by an earthquake [4], and urban heat island monitoring [5]. The temporal and spatial resolutions of remote sensing images acquired by different sensors are mutually limited, and these sensors are broadly divided into two main types. One type is equipped on the Landsat series, Gaofen series, Sentinel, and other satellites, and the other is the Moderate-resolution Imaging Spectroradiometer (MODIS). The Landsat series contains a diverse range of advanced thermal infrared sensors and mappers for mapping, which have different sensitivities to different bands. Remote sensing images required by the American Landsat series have a high-spatial resolution of 15–30 m and a revisit cycle of approximately 16 days. In contrast, remote sensing images obtained by MODIS on Terra/Aqua have a low-spatial resolution of 250 m–1 km and a revisit cycle of one day. However, it is difficult to obtain cloud-free image data for some months in many areas because of the interference of cloudy weather, which reduces the temporal resolution of the images to some extent. As sensor technology and deep learning improve by leaps and bounds, the research that uses STF methods to obtain HTHS resolution images has also attracted increasing attention [6]. STF is an effective method that can combine high-temporal–low-spatial (HTLS) remote sensing images with low-temporal–high-spatial (LTHS) remote sensing images to generate HTHS remote sensing images [7]. Although unmanned aerial vehicles (UAVs) can easily obtain HTHS resolution images, they do not apply to practical remote sensing applications for monitoring large surface areas because the image size they obtain is relatively small. In addition, it is difficult for UAVs to obtain images of depopulated zones, and most of the images obtained by UAVs are not publicly available, while remote sensing images obtained by satellites not only cover a wide area, but also most of them are free. Therefore, the major way to obtain HTHS images is through STF methods.

2. Related Work

In recent years, a large number of studies have been performed on STF methods for remote sensing images. According to different optimization strategies, STF methods can be roughly classified into four categories: transform-based STF methods, image reconstruction-based STF methods, hybrid pixel decomposition-based STF methods, and learning-based STF methods [8].

Transform-based STF methods involve wavelet transform and principal component analysis methods. STF methods based on wavelet transforms use wavelet transform technology to perform wavelet decomposition on remote sensing images and then fuse each decomposed layer, and the fusion results are ultimately acquired by the inverse wavelet transform [9,10,11]. In addition, methods based on principal component analysis first use a principal component method to separate the first principal component of high-spatial resolution remote sensing images and then extract the brightness component, and finally merge the extracted brightness image with the resampled low-spatial resolution remote sensing images to obtain fusion images [12].

The principle of the STF method based on image reconstruction is to calculate the weights of the similar adjacent pixels in input images and then obtain the target fusion images through interpolation according to the synthesis weights, including time and space. For example, Gao et al. [13] proposed a STF method STARFM, which is a new model that estimates adjacent pixels’ contribution to the reflectance of central pixels by calculating the weights of spectral difference, temporal difference, and pixel location distance. It is a relatively effective method for a study area where the reflectance of adjacent pixels varies little. To boost the pixel reconstruction of STARFM for nonuniform areas, Zhu et al. [14] proposed a STF method ESTARFM, which is an enhanced version of STARFM, that also searches for similar pixels first and calculates the weights of candidate pixels. The difference is that the ESTARFM calculates the weights of similar image pixels and transformation coefficients fully considering the internal relationship of the hybrid image pixels, which makes the experimental results of the algorithm in the region with high heterogeneity perform well compared with the STARFM method. A new STF model based on image reflectance changes (STAARCH) [15] proposed by Hilker et al., which is also inspired by STARFM, detects reflectance changes and denotes disturbances using Tasseled Cap transformations [16,17] of both Landsat images and MODIS image reflectance data.

The essence of the STF method based on unmixing is to unmix the spectral details of high-spatial resolution images at the prior time, and then predict the corresponding HTHS resolution remote sensing images [18]. For example, Zhukov et al. [19] proposed UMMF in 1999, which is a new STF model that first decomposes the spectrum of low-spatial resolution images and then fuses them with high-spatial resolution images to generate HTHS resolution remote sensing images. Based on UMMF, Wu et al. [20] proposed a new STF method STDFA, which considers the spatial and temporal variations in the calculation of the model and finally achieves good fusion results. These two methods require multiple high-spatial resolution images to guarantee fusion accuracy. However, the number of high-spatial resolution images obtained by sensors is limited due to cloud pollution in practical remote sensing applications. To solve this problem, Zhu et al. [21] proposed a flexible STF method FSDAF in 2016, which performs well in heterogeneous regions with a high speed by inputting a cloud-free and high-spatial resolution image.

Learning-based fusion methods can be roughly divided into dictionary-pair learning-based methods [8,22,23,24] and deep learning-based fusion methods. The algorithms based on dictionary-pair learning predict images by establishing the correspondence mainly according to the structural similarity between low- and high-spatial resolution images. For example, Huang et al. [22] proposed a STF network, SPSTFM, in 2012, a new model based on sparse representation, which is the first time to train dictionary pairs between high-spatial resolution residual images and low-spatial resolution residual images. However, this method is not practical in remote sensing applications because this STF method predicts HTHS images by using multiple high-spatial resolution images. Therefore, Wei et al. [23] proposed an optimization STF model in 2016, which predicts images based on semi-coupled dictionary-pair learning and structural sparsity. In 2021, Peng et al. [25] proposed a STF method, SCDNTSR, based on dictionary learning, which first considers the spectral correlation of image bands and further improves the accuracy of fusion results.

In recent years, deep learning has demonstrated its particular strengths in various fields. Inspired by the super-resolution structure of SRCNN [26] proposed by Dong et al., Tan et al. [27] proposed a STF model, DCSTFN, to predict images by using two branches dealing with spatial and temporal variation information separately. As the convolutional operation in feature extraction leads to the loss of details, EDCSTFN [28] was proposed based on DCSTFN, which added residual coding blocks and designed a compound loss function to improve the ability of extracted features. Considering the nonlinear mapping and super-resolution mapping between the input images, Song et al. [29] proposed the STFDCNN network, which designs two convolutional network branches to learn these two mappings separately and finally obtains the fused images through a weighting strategy. In addition, Liu et al. [30] proposed a fusion approach, StfNet, in 2019, which establishes the temporal dependence between low-spatial resolution images and predicts high-spatial resolution images according to the temporal consistency and the super-resolution technology. Tan et al. [31] proposed a STF model, GAN-STFM, based on unsupervised learning and obtained HTHS resolution images through only two images.

At present, there are still some problems with deep learning-based STF methods. First, the temporal change information and spatial features extracted from low-spatial resolution images by stacked convolutional layers are insufficient [18,27], and some details are lost during the upsampling process [32,33]. Second, a summation fusion strategy may result in poorly fused images due to a lack of consideration of global spatial feature information. To address the above issues, we propose a STF network architecture MANet based on multiscale and attention mechanisms. In MANet, we adopt three images for fusion. First, we obtained a residual image by performing a subtraction operation on two low-spatial resolution images, and then we input it into the whole network with a high-spatial resolution image. Our main contributions in this article are summarized as follows:

• A multiscale mechanism is used to extract temporal and spatial change information from low-spatial resolution images at multiple scales, which is to provide more detailed information for the subsequent fusion process.
• A residual channel attention upsampling (RCAU) module is designed to upsample the low-spatial resolution image. Inspired by DenseNet [34] and FPN [35] structures, the rich spatial details of high-spatial resolution images are used to complement the spatial loss of low-spatial resolution images during the upsampling process. This collaborative network structure makes the spatial and spectral information of the reconstructed images more accurate.
• A non-local attention mechanism is proposed to reconstruct the fused image by learning the global contextual information, which can improve the accuracy of the temporal and spatial information of the fused image.

The rest of the manuscript is organized as follows. Section 3 introduces the overall structure and internal modules of the MANet method. Section 4 describes the experimental part of the model, including the introduction of the datasets, the display of experimental results, and comparisons with other classical STF methods. Section 5 is our discussion, and Section 6 is the conclusion.

3. Materials and Methods

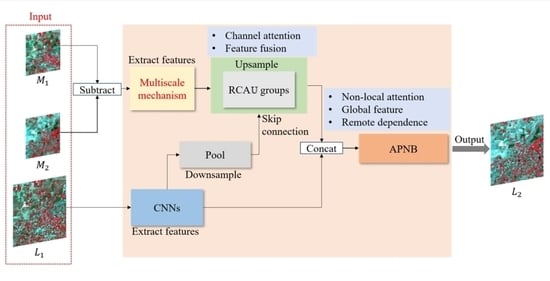
3.1. MANet Architecture

Figure 1 shows the overall architecture of MANet, in which cubes with different colors represent different convolution operations, ReLU activation functions and other specific operations. The MODIS image at time $t_i (i=1,2)$ is represented by $M_i$, and the Landsat image at time $t_i$ is represented by $L_i$. The MANet architecture contains three main parts:

• A sub-network is used to process residual low-spatial resolution images, extracting the temporal and spatial variation information.
• A sub-network is used to process high-spatial resolution images, extracting spatial and spectral information.
• To obtain more accurate fused images, a new fusion strategy is introduced to further learn the global temporal and spatial change information of the fused image.

We first obtain residual image $M_{12}$ by subtracting $M_1$ from $M_2$, which contains temporal and spatial variation information from time $t_1$ to time $t_2$. We then send this residual image to a multiscale mechanism to extract temporal and spatial change information at multiple scales. Since the size of the MODIS images we input is one-sixteenth that of Landsat images, we need to upsample them to the same size as the Landsat images for subsequent feature fusion. In addition, MODIS images contain fewer spatial details and may lose temporal and spatial information during upsampling. We design a new upsampling module named RCAU, which maintains more temporal and spatial detail information in useful channels during upsampling. Since MODIS images contain less spatial information than Landsat images, we use the rich spatial information of Landsat images to compensate for the loss of spatial feature information during the upsampling operation of MODIS images. We downsample Landsat images and then add the feature maps after downsampling with those of the upsampled MODIS images, and this operation helps to extract the spatial information of MODIS images in the upsampling process. We obtain high-spatial resolution images upsampled by 16 times with four RCAU modules. Meanwhile, we input the Landsat image at a prior time into three $5\times 5$ convolution kernel sequences to extract spatial details. Then, we fuse the upsampled feature maps containing temporal and spatial variation information with the feature map extracted from the Landsat image and obtain preliminary feature maps containing temporal and spatial information. In the process of feature fusion, the local temporal and spatial information of the feature map may be wrong. Therefore, we use an asymmetrical pyramid non-local block (APNB) [36] module to learn the global temporal and spatial information from the preliminary feature map and obtain the enhanced feature map. Finally, the feature maps obtained by the APNB module are sent to the two fully connected layers to obtain the final fusion image $L_2$, which integrates all the temporal and spatial information.

3.2. Multiscale Mechanism

The spatial structures of remote sensing images are very complex. In addition, convolution layers with a single receptive field are directly used to extract information, which may result in the loss of detailed information due to the limitation of the receptive field of convolutional layers. To address this issue, we use a multiscale mechanism [37] composed of convolutional kernels with different receptive fields to simultaneously extract temporal and spatial change features, which can improve the fusion accuracy. We input the residual feature maps obtained by subtracting MODIS images into this multiscale mechanism and then concatenate the obtained feature maps at different scales to acquire a feature map containing temporal and spatial variation information, as shown in Figure 2. This multiscale mechanism is composed of three $3\times 3$ convolution kernels, and their dilation rates are 1, 2, and 3, respectively. The larger the dilation rate is, the larger the receptive field of convolution layers, and the spatial and temporal change information may be more comprehensive. We extract features using three convolution layers with different dilation rates in parallel and then obtain the detailed feature information at different scales. In this article, the feature maps obtained by these three convolutional layers contain 12 channels, respectively, and then these feature maps are concatenated to acquire a feature map with 36 channels.

3.3. Attentional Mechanism

3.3.1. RCAU Module

Some spatial and temporal variation information in remote sensing images may be lost during the upsampling process. To retain more feature information in the upsampling process, we design an RCAU module to upsample remote sensing images and input the upsampled feature maps to a channel attention mechanism to adaptively assign weight to each channel according to the importance of channel details. This RCAU module is similar to the RCAB module [38], except that RCAU changes this first convolution layer to a deconvolution layer, which is to achieve the upsampling operation of MODIS images. The RCAB module integrates the channel attention mechanism and a residual block. The channel attention mechanism (CA) can adaptively assign weight to each channel according to the importance of channel details [39]. The residual block is used to combine deep features with shallow features in the network structure to reduce feature loss. The RCAB module has been proven to have a good effect on the application of single RGB image super-resolution [38]. Since the upsampling operation of remote sensing images is different from the super-resolution of natural images, the resolution difference of remote sensing images is approximately 16 times. In the RCAU module, a deconvolution layer is first used to double the spatial resolution, and the resulting feature maps are then sent to the ReLU activation and a convolution layer to further extract features. To reduce the spatial feature loss during upsampling, we use the channel attention mechanism to extract details more efficiently by acquiring dependencies between channels and restraining unnecessary information [40], as shown in Figure 3. Finally, we use a residual structure to add the feature map after the deconvolution operation to the feature map after the channel attention mechanism to fuse the information from shallow and deep network layers. To achieve the 16-times resolution scale fusion of remote sensing images, we need to use four RCAU modules in the MANet structure. For the layer nth (n = 1, 2, 3, 4) RCAU module, we have:

$$F_{n,b}=D_{n,b}\left(F_{n,b-1}\right)+C_{n,b}\left(X_{n,b}\right)\times X_{n,b}$$

(1)

where $C_{n,b}$ denotes the channel attention function, $F_{n,b}$ and $F_{n,b-1}$ are the input and output of the RCAU module, respectively, $D_{n,b}$ is the function that acts on the input feature map in the RCAU module, which contains the deconvolution and ReLU operations, and the RCAU learns the residual component $X_{n,b}$ from the input feature map. $X_{n,b}$ is composed of a Conv layer, which can be defined as:

$$X_{n,b}=W_{n,b}^1\times D_{n,b}$$

(2)

where $W_{n,b}^1$ represents the weight of the the Conv layer. $D_{n,b}$ is multiplied by the weight to obtain the residual component $X_{n,b}$. Therefore, the RCAU module not only increases the size of low-spatial resolution images by two times, but also the detailed texture information of low-spatial resolution images can be restored by using the rich spatial details of Landsat images, which is achieved by adding the feature maps of Landsat images that have been downsampled to the low-spatial resolution images. We then input the feature maps obtained after the four RCAU modules into the next convolutional layer to further extract detailed features.

3.3.2. APNB Architecture

The initial fused image was obtained by a simple addition operation, containing unitary information of spatial details and temporal changes, and the pixels of the image are independent of each other, which may produce jagged edges and noise. If we directly send it to a fully connected layer, the fusion image will contain more noise, and the fusion effect will be worse. Therefore, we used the non-local autocorrelation of the image to restore the non-local information of fusion image and improve the fusion result. This refers to an asymmetrical pyramid non-local block (APNB) module used in the MANet structure, which is an improved non-local model [41]. It realizes remote dependence by calculating the relationship between each query pixel and all the other pixels and aggregating the features of all pixels in the image. Thus, the relationship between pixels in the initial fusion image can be considered from the perspective of global details, making the fusion result close to the real image. It has been proven that APNB can be used to improve segmentation performance in semantic segmentation [42]. Figure 4 shows the network architecture of APNB module, where X is the input initial fusion image. The channels of this image are halved by three $1\times 1$ convolution layers, and the feature vectors Key, Value and Query are separately generated by flattening. Key and Query are used to calculate the similarity of pixels. Value represents the feature vector directly input to the network. To exploit multiscale correlations, the pyramid pooling layer structure was used for Key and Value to handle correlations at different scales. The adaptive average pooling layer was used to generate $1\times 1$, $3\times 3$, $6\times 6$, and $8\times 8$ matrices, which were flattened and connected into a vector. This vector was multiplied by the transposed Query to obtain a matrix containing correlations between different pixels. Afterward, the similarity weight was obtained by the softmax operation of this matrix, and then we multiplied the similarity weight by Value to obtain the feature map with global attention. Finally, to add the relationship between global pixels to the fused image, we sent the feature map to a reshape layer and a convolution layer, and then, the feature map was added to the initial fused image X. The latest fused image Y with a global relationship was obtained through two fully connected layers.

3.4. Loss Function

The MSE loss function is often used to evaluate the error between a predicted image and a real image in a STF model, which ignores the global quality of an image during the training process, we designed a compound loss function, which includes content loss and vision loss. The formula is:

$$L_{MANet}=L_{content}+\alpha \times L_{vision}$$

(3)

where $\alpha$ represents the weighting coefficient of vision loss. After many experiments, setting $\alpha$ to 0.8 worked best. The content loss is often used to ensure the pixel-level supervision of an image in a STF model, we use a Charbonnier loss [43] to calculate the content loss by calculating the pixel error between two images in this experiment. In content loss, the similarity between the real image and the predicted image is enforced by enhancing pixel-wise reconstruction, which can better process the outliers in the predicted image that are very different from the pixels in the real image. It can be defined as:

$$L_{content}=\sqrt{{(y-x)}^2+{ϵ}^2}$$

(4)

where x and y are the predicted value and the real observed value, respectively. The $ϵ$ is used to prevent the error backpropagation, which is empirically set to $1\times {10}^{-3}$. In the compound loss function, the content loss is to improve the similarity of the texture details between the predicted image and the real image, while the vision loss is to measure the visual similarity between images [44]. In the STF model, the multiscale structural similarity (MS-SSIM) [28,45] is used to calculate the vision loss, which is the multiscale version of SSIM. The SSIM index is used to comprehensively evaluate the similarity of images based on three parts: structure, contrast, and luminance, and it can also evaluate the structural similarity of images by calculating the mean, variance, and covariance between the real image and the predicted image. MS-SSIM is used to calculate the structural similarity of multiple levels after reducing the image to different scales, which reduces noise and blur around edges to obtain more accurate predicted images. Vision loss can be obtained by MS-SSIM, which can be defined as:

$$L_{vision}=1-\prod _{m=1}^M{\left(\frac{2{\mu }_x{\mu }_y+c_1}{{\mu }_x^2+{\mu }_y^2+c_1}\right)}^{{\beta }_m}{\left(\frac{2{\sigma }_{xy}+c_2}{{\sigma }_x^2+{\sigma }_y^2+c_2}\right)}^{{\gamma }_m}$$

(5)

where M represents the highest scale, ${\beta }_m$ and ${\gamma }_m$ represent the proportion of the two fractions, ${\mu }_x$ and ${\mu }_y$ represent the mean of the predicted image x and the real image y, respectively. ${\sigma }_x^2$ and ${\sigma }_y^2$ represent the variance of the predicted image x and the real image y, respectively. ${\sigma }_{xy}$ represents the covariance of the predicted image x and the real image y. $c_1$ and $c_2$ are two constants to ensure the stability of the formula.

The experimental results show that MS-SSIM can effectively restore the high-frequency characteristics of the predicted image [32]. Therefore, adding a vision loss function to the compound loss function can obtain more accurate prediction results.

4. Experiments

4.1. Datasets

To verify the effect of the proposed fusion model, we use two datasets to conduct the experiment. Figure 5a shows the Lower Gwydir Catchment (LGC) [46], which is located in northern New South Wales, Australia (NSW, 149.2815°E, 29.0855°S). This dataset contains 14 pairs of cloud-free MODIS-Landsat images from 16 April 2004 to 3 April 2005. MODIS images were obtained from MODIS Terra MOD09GA Collection 5 Data, and Landsat images were obtained from Landsat-5 TM and were atmospherically corrected using the algorithm [47] proposed by Li et al. The LGC dataset mainly takes the land cover area as the experimental area, including arid farmland, irrigated paddy fields, and forest land, and the spectral information in the area is more variable; thus, we mainly observe spectral changes [18]. The original LGC dataset image size is 3200 × 2720 and consists of six bands.

Figure 5b shows the Coleambally Irrigation Area (CIA) study cite [46], which is located in southern New South Wales, Australia (NSW, 34.0034°E, 145.0675°S). This dataset contains 17 pairs of cloud-free MODIS-Landsat images from 7 October 2001 to 17 May 2002. The MODIS images were obtained by MODIS Terra MOD09GA Collection 5 data, and the Landsat images were obtained by Landsat-7 ETM+ and were atmospherically corrected using MODTRAN4 [48] as outlined inVan Niel and McVicar [49]. On the CIA dataset, farmlands are mainly selected as the experimental area, and the phenological changes on different dates were obvious; thus, we take it as the dataset with high-spatial heterogeneity [18]. The original CIA dataset size is 1720 × 2040 and contains a total of six bands.

Before training the network, we first cropped all these images from the center to a size of $1200\times 1200$. The resolution difference between the original Landsat and MODIS images is 16 times, and we scale all the MODIS images to a size of $75\times 75$ for reducing training parameters. From Figure 6 and Figure 7, we can see the changes in the MODIS-Landsat image pairs of the CIA and LGC datasets on different dates, and the two datasets were input into the MANet structure for training. In these two datasets, we arranged the MODIS-Landsat image pairs in chronological order, and the temporally closest two image pairs were grouped in a data group according to the temporal distance. The time of the reference image is always before, and the time of the predicted image is always after. Finally, there are 16 data groups available in the CIA dataset and 13 data groups available in the LGC dataset. The grouped data is then randomly assigned to 60% of the dataset as the training dataset, 20% as the validation dataset, and the remaining 20% as the test dataset. In the whole experiment, the three parts of the datasets were selected assuming there was no intersection.

4.2. Evaluation Indicators

To make quantitative evaluations of our proposed STF model, we compared MANet with STARFM [13], FSDAF [21], DCSTFN [27], and DMNet [18] under the same conditions. We performed the same experiment on both datasets for all methods because these methods all use two low-spatial resolution images and one high-spatial resolution image for STF.

Firstly, we used the structural similarity (SSIM) index [50] to evaluate the similarity of two images from multiple perspectives. It can be defined as:

$$\mathrm{SSIM}(x,y)=\frac{(2{\mu }_x{\mu }_y+c_1)(2{\sigma }_{xy}+c_2)}{({\mu }_x^2+{\mu }_y^2+c_1)({\sigma }_x^2+{\sigma }_y^2+c_2)}$$

(6)

where ${\mu }_x$ and ${\mu }_y$ represent the mean of the predicted image x and the real image y, respectively. ${\sigma }_x^2$ and ${\sigma }_y^2$ represent the variance of the predicted image x and the real image y, respectively. ${\sigma }_{xy}$ represents the covariance of the predicted image x and the true image y. $c_1$ and $c_2$ are two constants to avoid system errors. The range of SSIM value is [−1, 1]. The larger the value of SSIM is, the smaller the difference between the predicted image and the real image; that is, the predicted image quality is better.

The second indicator is the peak signal-to-noise ratio (PSNR) [51], which is used to assess the loss of signal recovery. It can be indirectly defined by the mean square error (MSE), which refers to the mean of the sum of the squared differences between the predicted and the real image pixel values. MSE can be defined as:

$$\mathrm{MSE}=\frac{1}{mn}\sum _{i=0}^{m-1}\sum _{j=0}^{n-1}{\left|\right|y(i,j)-x(i,j)\left|\right|}^2$$

(7)

where m and n represent the height and width of the image, respectively. y and x are the real observed image and the predicted image. PSNR can be defined as:

$$\mathrm{PSNR}=20\times lo{g}_{10}\left(\frac{MA{X}_y}{\sqrt{MSE}}\right)$$

(8)

where $MA{X}_y$ represents the maximum possible pixel value of the real image y. The higher the value of PSNR is, the less distortion between the predicted image and the real image; that is, the predicted image quality is better.

The third index we used is the spatial correlation coefficient (CC) [52], which measures the spatial information similarity between the predicted image x and the real observed image y. It can be defined as:

$$\mathrm{CC}=\frac{{\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\sum }_{i=1}^n{(x_i-\overline{x})}^2{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}$$

(9)

The range of CC value is [−1, 1]. The closer the CC is to 1, the larger the positive correlation between the real observed image and the predicted image.

Finally, we used the root mean square error (RMSE) [27] index to measure the deviation between the predicted value x and the real observed value y. Specifically, it is the square root of MSE. It can be defined as:

$$\mathrm{RMSE}=\sqrt{\frac{1}{mn}\sum _{i=1}^m\sum _{j=1}^n{(y(i,j)-x(i,j))}^2}$$

(10)

where m and n represent the height and width of the image, respectively. y and x are the real observed value and the predicted value. The closer the RMSE is to 0, the closer the predicted image is to the real image.

4.3. Parameter Setting

STARFM [13] and FSDAF [21] are machine learning-based models that use 20% of the datasets to test directly in experiments without training. DCSTFN [27], DMNet [18] and MANet are all deep learning-based frameworks. MANet is a PyTorch-based framework that uses the Adam optimizer to optimize network training parameters. The weight attenuation is set to $1\times {10}^{-6}$, the initial learning rate is set to 0.0008, and the training epoch is set to 30. We trained MANet for 6 h in a Windows 10 professional environment, equipped with 16 GB RAM, an Intel Core I5-10400 CPU @2.90 GHz, and a NVIDIA GeForce RTX 3060 GPU.

4.4. Experiment Results

4.4.1. Subjective Evaluation

Figure 8 shows the prediction results of various fusion methods on the CIA dataset on 26 April 2002. “GT” represents the real image, and “Proposed” is our MANet method. As Figure 8 shows, the field of the CIA dataset is relatively small, and it has strong spatial heterogeneity. For better visual comparison, we extracted and enlarged the sharp contrast part. The figure shows that all the fusion methods can improve the spatial resolution of the predicted images to a certain extent, indicating that these fusion methods can roughly recover the temporal changes, spatial variations, and spectral change of the predicted images. However, in some heterogeneous regions, the fusion results of different fusion methods are different. As shown in the figure, the fusion results of the STARFM fusion method and FSDAF fusion method have been seriously distorted in spectral details. The “GT” image shows a white area, while the STARFM predicted image shows obvious purple patches and loses texture details. This may be because the STF method is heavily affected by the search window during the process of image pixel prediction and performs poorly when the image has high-spatial heterogeneity. In the FSDAF predicted image, there are also some purple patches, and the edge of the farmland is fuzzy. This may be because the fusion method uses a TPS algorithm to predict high-spatial resolution images from low-spatial resolution images. As the figure shows, the spectral information of the white area of the DCSTFN predicted result experienced an error, and the fuzzy effect also appeared at the edge of farmland, which may be caused by the loss of spatial information after using multiple convolution layers. Although the results predicted by the DMNet fusion method show good texture details and the spatial information was retained relatively completely, the spectral distortion was relatively serious, which might be related to the use of a simple addition method for fusion. For our proposed method, the farmland edge information is well processed. Although the spectral information is not accurately reflected, the color difference is relatively small, and the white area is partially restored, making it relatively similar to that of the real image. This shows that our proposed method has a better effect on the high-spatial heterogeneity dataset than the other fusion methods. This is because we paid more attention to extracting spatial and temporal details by introducing a multiscale mechanism.

Figure 9 shows the prediction results of various fusion methods on the LGC dataset on 2 March 2005. “GT” represents the real image, and “Proposed” is our MANet method. Since the variation of spectral information on the LGC dataset is large, we mainly compared the spectral changes and boundary information of the fusion results. For visual comparison, we also extracted and enlarged the sharp-contrast part. As the figure shows, all fusion methods can achieve good prediction of spatial details in most areas. However, in some regions where the spectral information changes greatly, the prediction results of each fusion method are different. As shown in the figure, the predicted images of the STARFM fusion method and FSDAF fusion method exhibit spectral distortion. A red line is shown in the “GT” image, but there are red patches in the STARFM predicted image, which is a serious spectral distortion. This is because STARFM uses surrounding pixels to reconstruct the central pixel, which results in spectral distortion because it is not conducive to the restoration of boundary details. Some black patches in the red area of the “GT” image disappeared in the STARFM predicted image, indicating that spectral changes and boundary information of the STARFM fusion method were lost, which may be caused by the settings of the search window. As shown by the FSDAF prediction results, although the red patches are reduced, there is still spectral distortion, which may also be due to partial information lost in the prediction process and the TPS interpolation operation. The methods based on machine learning performed poorly in processing boundary details in the region where spectral information varies greatly. The DCSTFN and DMNet STF approaches still have some fuzzy phenomena in processing boundary information. In the DCSTFN prediction results, the red line is not smooth enough, and the texture details are not well processed. This may be caused by the loss of detailed information during the process of using multiple convolutional layers in this method. DCSTFN and DMNet can recover the spectral information of the image to some extent. The predicted result of our method is smoother than that of others methods in processing the red line, and the spectral information and boundary information can be well predicted. In general, compared with other fusion methods, our proposed method not only achieves accurate prediction of texture details, but also processes the spectral details well.

4.4.2. Objective Evaluation

Table 1. Quantitative assessment of different STF methods on the CIA [46] dataset.

Evaluation	Band	Method
		STARFM	FSDAF	DCSTFN	DMNet	Proposed
SSIM	Band1	0.8731	0.9037	0.9355	0.9368	0.9455
	Band2	0.8527	0.9172	0.9304	0.9304	0.9351
	Band3	0.7938	0.8578	0.8915	0.8905	0.8989
	Band4	0.7329	0.8210	0.8231	0.8271	0.8319
	Band5	0.7197	0.8109	0.8165	0.8187	0.8274
	Band6	0.7260	0.8194	0.8383	0.8379	0.8432
	Average	0.7830	0.8550	0.8726	0.8736	0.8803
PSNR	Band1	27.4332	37.2104	38.3779	38.3696	39.2152
	Band2	24.3359	36.0368	36.4337	36.3136	36.8910
	Band3	24.5396	31.3339	33.2257	32.8116	33.2862
	Band4	19.6533	26.9470	28.7492	28.5944	28.8370
	Band5	20.8408	28.0493	28.4029	28.1894	28.5474
	Band6	22.1580	25.0635	29.8863	29.7228	29.9921
	Average	23.1601	30.7735	32.5126	32.3336	32.7948
CC	Band1	0.3898	0.8014	0.8374	0.8382	0.8547
	Badn2	0.3965	0.7988	0.8603	0.8581	0.8658
	Band3	0.5883	0.8302	0.8912	0.8854	0.8882
	Band4	0.5039	0.8161	0.8265	0.8195	0.8272
	Band5	0.6855	0.8977	0.9015	0.8989	0.9060
	Band6	0.6927	0.9060	0.9153	0.9126	0.9162
	Average	0.5428	0.8417	0.8720	0.8688	0.8764
RMSE	Band1	0.0124	0.0124	0.0123	0.0122	0.0112
	Band2	0.0156	0.0162	0.0156	0.0158	0.0149
	Band3	0.0227	0.0234	0.0226	0.0239	0.0229
	Band4	0.0387	0.0408	0.0387	0.0395	0.0385
	Band5	0.0386	0.0399	0.0386	0.0394	0.0382
	Band6	0.0330	0.0329	0.0324	0.0330	0.0324
	Average	0.0268	0.0276	0.0267	0.0273	0.0264

shows the quantitative evaluation results of various fusion methods on the CIA dataset with high-spatial heterogeneity. The best values of the index are marked in bold. As the table shows, the prediction results of our proposed MANet fusion method are improved in terms of most indicators compared with those of other algorithms. For example, in terms of the SSIM index related to spatial information, the result of our proposed method is approximately 2.9% higher than that of the FSDAF fusion method based on machine learning. Compared with the DMNet method based on deep learning, the SSIM values of our method are improved by about 1% on multiple bands. These show that our proposed method can handle spatial variation information of the dataset with high-spatial heterogeneity well. The quantitative evaluation results obtained by the STARFM fusion method are the worst, which may be because the surrounding pixels are used for pixel reconstruction, which is not applicable in a region where spatial information changes greatly. The poor quantitative evaluation result of the FSDAF fusion method may be due to the limitation of the TPS interpolation algorithm. The spectral information is related to RMSE and CC values, and the value of RMSE represents the pixel-level error between the predicted image and the real image in particular. In the quantitative evaluation results of the DCSTFN STF method, the indices of some bands are the best, which shows that DCSTFN can predict the spectral information of these bands well. The SSIM value of DMNet method is better than that of DCSTFN method, which indicates that DMNet can better handle spatial variation information. The values of CC and RMSE of DMNet method are both worse than those of the DCSTFN method, which indicates that DCSTFN method can predict spectral information well. This may be because the DMNet method uses a simple addition strategy for fusion and ignores some useful information. The MANet method acquired the best results on other indexes, such as RMSE and CC values, which indicates that our proposed method can better predict spectral change information. The experimental results indicate that the spatial details and spectral change information of remote sensing images can be better captured by adding multiscale and attentional mechanisms to the network structure.

Table 2. Quantitative assessment of different STF methods on the LGC [46] dataset.

Evaluation	Band	Method
		STARFM	FSDAF	DCSTFN	DMNet	Proposed
SSIM	Band1	0.8846	0.9264	0.9361	0.9368	0.9384
	Band2	0.8837	0.9300	0.9489	0.9304	0.9488
	Band3	0.8401	0.9241	0.9262	0.8905	0.9303
	Band4	0.8071	0.8803	0.8901	0.8971	0.8975
	Band5	0.7860	0.8693	0.8706	0.8687	0.8842
	Band6	0.7908	0.8615	0.8714	0.8779	0.8804
	Average	0.8321	0.8986	0.9072	0.9002	0.9133
PSNR	Band1	30.4687	38.5891	39.0567	39.5980	39.6168
	Band2	23.3251	37.1057	38.0523	38.1447	38.2195
	Band3	23.6144	35.0483	35.9674	35.7742	36.0948
	Band4	17.4570	31.2650	31.5236	31.4327	31.8561
	Band5	20.3062	30.2034	30.9916	30.8822	31.2151
	Band6	21.9842	31.0435	32.1594	31.9054	32.2980
	Average	22.8593	33.8758	34.6252	34.6229	34.8834
CC	Band1	0.7697	0.8802	0.8973	0.9012	0.9090
	Band2	0.8775	0.8901	0.8943	0.8939	0.9003
	Band3	0.8272	0.8969	0.9052	0.9067	0.9079
	Band4	0.8993	0.9090	0.9198	0.9183	0.9209
	Band5	0.7816	0.9216	0.9263	0.9242	0.9298
	Band6	0.7270	0.9203	0.9228	0.9252	0.9264
	Average	0.8137	0.9030	0.9110	0.9116	0.9157
RMSE	Band1	0.0122	0.0139	0.0122	0.0119	0.0117
	Band2	0.0134	0.0132	0.0130	0.0130	0.0131
	Band3	0.0164	0.0167	0.0162	0.0166	0.0163
	Band4	0.0268	0.0276	0.0268	0.0271	0.0259
	Band5	0.0291	0.0297	0.0291	0.0298	0.0286
	Band6	0.0277	0.0271	0.0257	0.0266	0.0254
	Average	0.0209	0.0214	0.0205	0.0208	0.0202

shows the quantitative evaluation results of various fusion methods on the LGC dataset with large spectral changes. The best values of the index are marked in bold. As the table shows, the prediction results of our proposed MANet fusion method are improved in terms of most indicators compared with those of other algorithms. For example, the result of our proposed method is approximately 1% higher than those of other methods in terms of the SSIM index, which indicates that our proposed method can handle spatial variation information. Spectral variation is related to RMSE and CC indexes, the result of our proposed method is improved to a certain degree compared with other methods, which indicates that our proposed method can better predict spectral change information. The quantitative evaluation results of the STARFM fusion method are the worst and with serious spectral distortion, because the method uses the surrounding pixels to predict center pixels with the limits of the search window, so it cannot be applied to the area with great spectral changes. The quantitative evaluation results of the FSDAF fusion method are poor compared with those of the STF methods, which may be because this method uses the TPS interpolation algorithm to predict high-resolution images and finally uses the information of adjacent regions to obtain the predicted images, which leads to spectral distortion due to information loss. In the quantitative evaluation results of the DCSTFN fusion method, the RMSE index values of some bands are optimal, which indicates that DCSTFN method can predict the spectral change information to some extent. The quantitative evaluation results of the DMNet fusion method are inferior to those of DCSTFN because it loses information through an additive fusion strategy. Table 2 shows that our method achieves the best quantitative evaluation results on the SSIM, RMSE, PSNR, and CC indexes. This is because we use high-spatial resolution image features to help restore the spectral information and spatial details of the predicted image. Finally, a non-local attention mechanism is used to pay more attention to the spatial and spectral relations between pixels. This shows that our method can be better applied to regions with large spectral changes.

5. Discussion

The experimental results obtained on the CIA dataset show that our method acquired the best result by introducing multiscale and attention mechanisms and a compound loss function in heterogeneous regions. The subjective evaluation shows that the prediction results of the STARFM fusion method and FSDAF fusion method both exhibit serious spectral distortion, while the image predicted by our proposed STF method is relatively closer to the real image. This shows that our method can predict the spectral variation, temporal variation, and spatial features of images in heterogeneous regions. Second, the experimental results obtained on the LGC dataset show that our method can better predict the spectral changes in regions with great spectral changes because our method pays more attention to extracting details and incorporates a new fusion method to retain more detailed features. The following was achieved with the MANet method: (1) feature extraction of low-spatial resolution remote sensing images is realized by using a multiscale mechanism; (2) the upsampling of low-spatial resolution images is performed by using the RCAU module; and (3) a new fusion strategy is introduced to further learn the global temporal and spatial change information of the fused image, which can obtain a more accurate fused image. We use the RCAU module to upsample low-spatial resolution images, in which the channel attention mechanism captures the spatial and spectral details during the upsampling process. Similarly, after the initial fusion image is generated, we send it to the APNB module so that we can capture global information of the predicted image according to the indexes of time and space. Thus, we can obtain more accurate prediction results.

5.1. Ablation Experiments

Three experiments were designed to further describe the importance of the multiscale mechanism, the RCAU module, and the APNB module. In the first experiment, we replaced the multiscale mechanism with an ordinary convolution and retained the RCAU module and the APNB module. In the second experiment, we removed the RCAU module and retained the multiscale mechanism and the APNB module. In the third experiment, we removed the APNB module and retained the multiscale mechanism and the RCAU module.

Table 3. The results of comparative experiments.

Dataset	Index	ANet	MAPNet	MRNet	MANet
CIA	SSIM	0.8794	0.8791	0.8788	0.8803
	RMSE	0.0266	0.0267	0.0267	0.0264
LGC	SSIM	0.9132	0.9131	0.9133	0.9133
	RMSE	0.0203	0.0204	0.0203	0.0202

shows the results of Experiment 1, Experiment 2, and Experiment 3, in which “ANet” refers to the network structure with the multiscale mechanism removed, “MAPNet” refers to the network structure with the RCAU module removed, and “MRNet” refers to the network structure with the APNB module removed. The best values of the index are marked in bold.

As the above table shows, on the CIA dataset, the SSIM value of ANet is greater than that of MRNet and that of MAPNet, which indicates that ANet is better than MRNet and MAPNet in predicting spatial change information. The RMSE value of ANet is less than that of MRNet and that of MAPNet, which indicates that the predicted result of ANet is more accurate than that of MRNet and that of MAPNet in predicting spectral change information. These show that adding attention mechanisms is beneficial to feature extraction of the spectral and spatial variation information. On the LGC dataset, the SSIM value of MRNet is larger than that of MAPNet and that of ANet, which indicates that the predicted result of MRNet is better than that of MAPNet and that of ANet in predicting the spatial change information. The RMSE values of MRNet and ANet are smaller than that of MAPNet, which indicates that MRNet and ANet are better than MAPNet in predicting spectral change information. These show that adding multiscale and attention mechanisms is beneficial to feature extraction of the spectral and spatial variation information. The SSIM and RMSE values of MANet on the CIA dataset and LGC dataset are optimal, which indicates the MANet method can better extract spatial and spectral information compared with other STF methods. Figure 10 shows the results on the CIA dataset of these three comparative experimental methods and our proposed method with band 4 on 26 April 2002. Figure 11 shows the results on the LGC dataset of these three comparative experimental methods and our proposed method with band 4 on 28 December 2004.

In Figure 10 and Figure 11, (a) represents the real image, (b) represents the ANet predicted image, (c) represents the MAPNet predicted image, (d) represents the MRNet predicted image, and (e) represents the MANet predicted image. Figure 10 shows that the ANet predicted image has obvious spectral distortion. The predicted images of MAPNet, MRNet, and MANet are more similar to the real observed images, which indicates that adding a multiscale mechanism can effectively extract the temporal changes and spectral details of images. The ANet method performs well in terms of the quantitative evaluation results, possibly because texture details are lost in the MAPNet and MRNet fusion methods. MANet performs best in terms of quantitative evaluation results, which shows that adding a multiscale mechanism can effectively extract the temporal changes and spectral details and adding attention modules can effectively extract spatial details. As Figure 11 shows, the predicted images of MAPNet and MRNet exhibit spatial and spectrum detail loss, which shows that using the attention mechanisms to extract temporal and spatial details for subsequent image recovery is important in regions with large spectrum variation. Comparatively, the MANet predicted image is more similar to the real image, which indicates that our method can deal well with spectral and spatial details. Although we improved the method of extracting spatial information and spectral details, our study still has deficiencies, such as the prediction accuracy of our method for areas with large topographic variations. Once we have collected enough qualified datasets, we can design a more suitable network structure for more advanced analysis.

5.2. Loss Curves and the Number of Training Parameters

Table 4. The number of training parameters for various fusion methods.

Method	STARFM	FSDAF	DCSTFN	DMNet	MANet
Training parameters	-	-	298,177	327,061	77,171

shows the number of training parameters for various fusion methods. STARFM and FSDAF are fusion methods based on machine learning, so they have no training process. As the table shows, our fusion method has fewer training parameters than other deep learning-based fusion methods. In training the network, the whole dataset is trained in each epoch. As the number of training epochs increases, the accuracy of model training increases. We input the dataset into the MANet structure according to the number of bands to optimize the weights of the network. Figure 12 shows the evolution of the loss curves at the training stage and validation stage for 30 epochs, where each color represents a different band and the solid line and dotted line represent the loss curves at the training stage and validation stage, respectively. Since the loss function is composed of content loss and vision loss, the closer it is to zero, the better the training effect. We can see from Figure 12 that the training loss value decreases rapidly at first and then stabilizes and no longer decreases after 20 epochs, while the validation loss is not stable and fluctuates greatly in the early stage. After more than 25 epochs, all the loss function curves show a relatively stable trend. Therefore, the network tends to converge when the number of epochs is greater than or equal to 30.

6. Conclusions

We evaluated the effectiveness of our proposed STF method MANet by using two datasets with different characteristics and acquired the best final experimental results. The main contributions of our research are introducing a new STF architecture, which includes the following:

• The multiscale mechanism is used to extract the temporal and spatial variation of a low-spatial resolution image. The final experimental results indicated that the extraction of detail features at different scales can make the network retain more useful temporal and spatial details, and the prediction result is closer to the real result.
• By designing the RCAU module, we not only realize the upsampling of feature maps with low-spatial resolution, but also reduce the loss of detail information by the weighting operation, which is more conducive to the reconstruction of low-spatial resolution image pixels.
• In the fusion process, we have designed a new fusion strategy. The APNB module was added after the initial fusion image, which can effectively extract global spatial and temporal information. Experimental results show that our method can better capture the spatial details and spectral information of the predicted image.

The experimental results show that our method achieves the best prediction results on both the CIA dataset with complex spatial information and the LGC dataset with variable spectral information. From the perspective of the whole fusion framework, the feature information of low-spatial resolution images and the rich spatial information of high-spatial resolution images are both important for predicting HTHS resolution images. The low-spatial resolution image easily loses details in the upsampling process, so we introduce attention mechanisms to restore its spatial resolution and spectral information with the help of channel weights, which is significant in solving temporal and spatial problems. In the STF problems, due to the limitation of fewer available datasets, the predicted accuracy is difficult to greatly improve. Therefore, future research must map low-spatial resolution images to high-spatial resolution images without reference in the prediction stage. These problems can be further discussed.