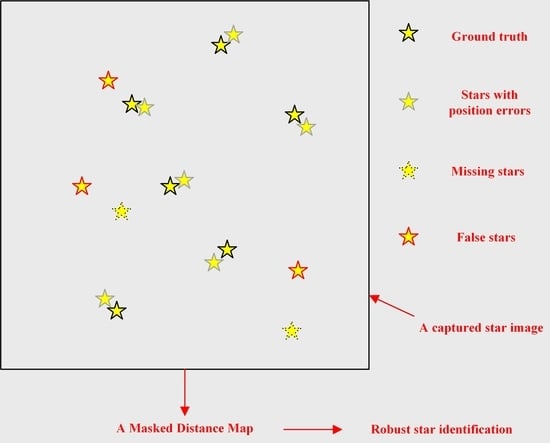
A Robust Star Identification Algorithm Based on a Masked Distance Map

Abstract

The authors of this paper propose a robust star identification algorithm for a ‘Lost-In-Space’-mode star tracker for lost-cost CubeSat missions. A two-step identification framework and an embedded validation mechanism were designed to accelerate the process. In the first step, a masked distance map is designed to provide a shortlist of stars, and the embedded fast validation process enables the direct output of validated stars before the second step. In the second step, local similarity is utilized to select a set of stars from those shortlisted, and the final validation procedure rejects all unsatisfactory stars. This algorithm can provide reliable and robust recognition even when the captured star images include severe star positioning errors, missing stars and false stars. The proposed algorithm was verified by a simulation study under various conditions. As low-cost star sensors face harsh and unknown environments during deep space CubeSat missions such as asteroid exploration, the proposed algorithm with high robustness will provide an important function.

1. Introduction

Star sensors are passive optical sensors that can determine star attitudes by observation and identification. Due to their high accuracy and integration, star sensors are widely used in various space missions [1]. By identifying stars extracted from a captured star image, a star sensor determines the inertial direction of the optical axis with arcsecond-level accuracy [2,3]. Many mature algorithms for calculating a star sensor’s optical axis direction in inertial space given the vectors of multiple stars exist, e.g., QUEST, FOAM, SVD, and TRIAD [4,5]. The classical star sensor is a relatively complex system and was until recently used only in high-end missions. However, with the rise of CubeSats and other low-cost satellites [6,7,8,9,10], some low-cost options have emerged [11]. Arguably, one of the most important components of a star sensor system is the star identification algorithm. The low-cost star sensors bring many challenges to the star identification algorithm, among which the robustness of star identification algorithms has attracted much attention.

When a star sensor initializes or recovers from a fault, it works in the ‘Lost-In-Space’ mode, with no available prior attitude information [12]. A star identification algorithm is needed to identify a captured star in whole-sky images, and the development of this type of algorithm is quite challenging. At present, existing algorithms transform the star identification problem into a matching problem by building a feature database or template database in advance and searching for a captured star in the database, which is a process based on the hypothesis that a star image is completely separable under certain patterns. Specifically, these algorithms can be divided into two main categories for the feature extraction phase, namely: subgraph-isomorphism-based feature extraction and pattern association feature extraction [1]. The basis of a subgraph isomorphism method [13,14] involves using star points extracted from an image to construct simple geometric shapes (such as line segments [15], polygons [16,17,18], and pyramids [19]) and extract shape features (such as angles [20], side lengths [15], and areas [16]) for matching in a feature database built in advance. Its core lies in using the invariance of geometric features [21]. In comparison, a pattern association method constructs a unique pattern from the distribution of extracted stars and identifies the most similar template in a template database. Typical pattern recognition methods include the grid method [22], polar grid method [23,24,25], and statistical feature method [26]. Comparatively speaking, pattern recognition methods have advantages in database size, recognition speed and robustness to noise [27]. In addition, neural networks are also applied to star image recognition [28,29,30]. The neural-network-based method is reported to have strong robustness to various noises, and it does not require operations such as rotation and translation alignment [29,30,31]. Missing stars will significantly decrease accuracy because the learned template will change. Neural-network-based methods still need artificially designed initial features, such as traditional features [30,31] and generated pattern pictures [29], as input. Then, templates can be learned through neural network training, which is actually a feature enhancement transformation. In addition, a self-organization map is also used to reduce the dimension of the high-dimensional input space [32]. The reported methods are mostly based on 15° × 15° and 20° × 20° field of view (FOV), and the performance for smaller FOV needs to be verified. The neural-network-based approaches should also be used with a validation method [33] to avoid misidentification. Compared with conventional star identification algorithms, the neural-network-based approaches can achieve a time complexity of only O(1), but these neural networks contain fully-connected layers and require relatively large but constant amounts of memory. Singular value decomposition (SVD) is another novel star pattern recognition algorithm method that does not need a separate attitude determination algorithm; rather, it directly produces the attitude, and a reliability evaluation using star voting was introduced to relieve the problem of redundant matches [34].

At present, deep space exploration is undergoing rapid promotion [35]. Deep space missions, especially these with low-cost CubeSats, involve many severe challenges for star identification. Due to long-term and long-distance flights, complicated environments, and low-cost sensor system, star sensors may suffer from calibration errors, performance degradation, lens contamination and other problems. If a star sensor fails, the associated spacecraft and mission may be jeopardized. These problems impose more stringent requirements on the robustness and reliability of star identification algorithms. Both identification accuracy and identification speed are important criteria for algorithm evaluation, and a trade-off must be considered. On the one hand, to obtain a higher identification accuracy, more complex features and feature combinations are preferred for use in template matching, but this will increase the computational complexity and lower the recognition speed of the algorithm. On the other hand, although the computational complexity can be reduced by reducing or simplifying the extracted features, the identification accuracy may become weak and unreliable. Therefore, the algorithm identification accuracy and speed should be balanced, and appropriate algorithms must be designed to meet the requirements of specific scenarios.

Fruitful research has been conducted to improve the computational efficiency and robustness of star identification algorithms. To improve the identification speed, database structures have been optimized to reduce their size and facilitate uploading and updating procedures [36]. Database-searching process has been accelerated by introducing data structures such as binary trees [37], search trees [24,38], k-vectors [39,40,41], and labels [42]. To speed up the star image recognition convergence process, several methods, such as step-by-step searching [43,44], iterative searching [45], and hash searching [46], have been proposed. Research has also increased the speed of the recognition process by using brightness information [47]. Recent work also includes optimizing the parameters of the grid method with optimization methods [48] and by introducing an attitude estimation step to accelerate the validation of the results of star pattern recognition [33]. Regarding robustness, elastic template matching has been proposed to increase the robustness of the traditional grid method [23,24], and a distance transform [49] has been used to construct robust features for star map recognition [50,51]. The problem of star identification in the presence of high slew rates, false objects and image deformations introduced by the rolling shutter has also been addressed [52].

In this paper, we first analyze the problems that star pattern recognition algorithms face under adverse circumstances and the incapability of existing algorithms in the face of these problems. To solve the identified problems, we then redesign the method of reference star selection and propose a method to construct the closest neighboring star set. Later, through an illustrative example, we describe the combination of a two-step framework that uses a masked distance map for shortlisting and a local similarity scale for successive identification, with an embedded verification mechanism to achieve robust star identification. In the first step, the masked distance map is designed to provide star shortlisting, and fast validation enables the direct output of validated stars before the second step. In the second step, local similarity is utilized to select a star from those shortlisted, and the final validation refuses all unsatisfactory stars. The subsequent sections describe the details of the research problem and the proposed approach, simulation, and benchmarking with existing star pattern recognition techniques. The paper concludes with an analysis of the performance and application prospects of the proposed algorithm.

The main contributions of this paper are:

(1)

Local scope is introduced to design a masked distance map to further improve the robust of shortest distance transformation.

(2)

The introduction of false stars causes very few misidentifications by the proposed algorithm.

(3)

The identification rate of our algorithm is high with noise, and it is also efficient.

2. Problem

This section presents the problems that star pattern recognition algorithms face under adverse circumstances and the incapability of existing algorithms in the face of these problems. Several concepts are demonstrated since they are important for our method.

2.1. Noise and Interfering Stars

The main challenge in star pattern recognition comes from noise and interfering stars, which can affect the accuracy of a star sensor’s attitude output, as shown in Figure 1. Two kinds of noise exist: star positioning errors and magnitude (brightness) noise. Star positioning errors mainly occur due to calibration errors of the star sensor (such as focal length errors, lens distortion, and optical axis offset errors) and errors in the star point positioning algorithm [53] (such as those caused by motion blur). Magnitude noise indicates the uncertainty of a sensor’s brightness sensitivity calibration. The interfering star problem causes two effects: false stars (spikes) and missing stars. The main cause of false stars is the appearance of celestial bodies, space debris, etc., that are difficult to distinguish from true star points in the FOV of the star sensor. This issue may also be caused by hardware defects, such as hot detector pixels. The other interfering star effect, missing stars, arise when stars in the navigation star database that should have been captured do not appear in the FOV due to a calibration error in the sensor’s brightness sensitivity.

A calibration error is not the only cause for missing stars. Even in a perfectly calibrated star tracker, missing stars may arise due to noise (e.g., if the noise causes the star signal of a weak star, near the limiting magnitude, to fall below the detection threshold of the image segmentation/star detection algorithm). Additionally, random noise in an image may augment the signal of weak stars that were not included in the on-board star catalog just because their magnitudes were just beyond the cut-off magnitude used when building the on-board catalog, making them temporarily visible in a star tracker image/frame. In addition, calibration errors in the sensor’s brightness sensitivity can also cause false stars when stars that are not stored in the database and those with weaker brightness are captured in the FOV without corresponding matches in the template database.

In this paper, the sensitivity of the star sensor used in the following discussion and simulation was 6.3. The resolution of the sensor was 1024 × 1024, and its FOV was 15° × 15°, with the SAO catalog [54] as the base catalog.

2.2. Shortcomings of Existing Algorithms

Traditional methods such as the grid method generally consist of reference star selection, closest-neighbor star selection, registration, feature extraction, matching, and validation. Registration refers to the process in which a captured image is translated and rotated for comparison to the database, as shown in Figure 2. Most of these methods only focus on feature extraction and matching and do not consider reference star selection, closest-neighbor star selection and validation. The reference star to be identified is usually selected as the point closest to the center of the field of view, and the nearest-neighbor point is only judged according to hard criteria. Moreover, verification requires the introduction of additional reference stars.

We performed four studies using 64,800 stars. The results revealed several problems in the traditional method.

(1)

In the first study, we checked the number of stars remaining in the FOV after the registration process by selecting the point closest to the center of the FOV as the reference star to be identified. According to the results, 12.67% of stars in the FOV were transformed out of the FOV during registration, as shown in Figure 3, which reduced the number of available stars. The utilization rate of stars was low, and the pattern information became sparse, which was not conducive to the subsequent feature extraction and matching processes. In some cases, the number of star points in star images was less than 5; thus, it is very important to retain more star points for the identification of star maps containing fewer star points

(2)

In the second study, we analyzed the number of incorrect choices of closest-neighbor stars in an image by applying hard criteria. According to the results, the incorrect selections of the nearest-neighbor star occurred in 0.62% of star images. Under the hard criteria, only one nearest-neighbor star was selected, and its selection error rate increased in the presence of noise and interfering stars, directly leading to subsequent matching errors. Generally, the overall identification accuracy can only be improved by continuously introducing additional reference stars in the verification step [55]. Among the incorrect selections, as shown in Figure 4, 86 cases (0.13%) were caused by the absence of the nearest star in the FOV, while 315 cases (0.49%) were caused by star positioning errors of multiple star points.

(3)

In the third study, we analyzed the robustness of traditional feature extraction to positioning errors. Because traditional feature extraction does not make full use of the spatial similarity of stars in an image, it has poor robustness to interfering stars, as shown in Figure 5. It is clear that star points located at the edge of the grid may cause grid feature extraction errors in the case of positioning errors. Better feature extraction should reflect the differences in positions. Therefore, more attention should be given to the spatial distribution characteristics of star points in feature extraction.

(4)

The fourth study was performed to analyze the efficiency of the traditional validation method. The traditional method requires the repeated introduction of an additional reference star, which involves high computational complexity and greatly reduces the overall efficiency of the identification algorithm. As shown in Figure 6, it is necessary to continuously introduce a reference star to verify and identify star points until all star points are individually identified. After identification fails for all extracted stars, the image will be refused. It was found that the refuse mechanism has a low efficiency.

Our method considers the selection of the reference star and the nearest-neighbor star to maximize the number of stars remaining in the FOV after registration and to decrease incorrect selections of closest-neighbor stars. In addition, a masked distance map and local similarity are introduced into two-step matching, and an embedded validation mechanism is applied to avoid repeated verification.

The rest of this paper is structured as follows. Section 3 describes the methods of reference star selection, closest-neighbor star set identification, feature extraction, template database construction, two-step matching, and embedded validation in detail. Example simulation and benchmarking results are shown in Section 4. Finally, concluding remarks are presented in Section 5.

3. Method

First, we briefly introduce the features extracted for comparison between a captured image and the template database. Second, the construction of the template database is presented. Third, registration between a captured image and the template is described in detail, which is a process based on the selection of a reference star and closest-neighbor star set under flexible criteria. Then, the two similarity criteria used in two-step matching are introduced, followed by a discussion of the two validation steps embedded into two-step matching. Finally, a schematic overview of the algorithm is presented.

3.1. Pixel Coordinate Feature

The proposed algorithm directly uses the pixel coordinates of stars as raw features. Compared with geometric feature matching algorithms in which the pixel coordinates of stars are usually converted to unit vectors, our method benefits from lower computational complexity and a smaller database size. The pixel coordinate features extracted from the camera image need to be compared to those extracted from a star catalog, which, in this case, is the SAO J2000 catalog [54]. On the one hand, pixel coordinate features can be seen as the most intensive grid, which enables the maximum utilization of the spatial geometry information in a star image. On the other hand, the geometrical relations between pixel coordinates have moderate robustness to rotation and translation when applied to the narrow or middle FOV of a star sensor, as in this paper. In addition, due to the gnomonic projection of a small patch of the celestial sphere surface onto the imaging plane of a star sensor, the introduction of distortions into star images is inevitable, even with an ideal distortionless pinhole camera model. A robust two-step matching process was carefully designed to handle this problem and was evaluated in the simulation.

3.2. Construction of the Template Database

Stars with magnitudes of less than 6.3 are used to form the template database. Each star in the template database is considered individually at the center of the FOV and is used together with all nearby stars within the pattern radius to extract the abovementioned features. The pattern radius is equal to the number of pixels corresponding to the size of the FOV. The relation between the pattern radius ($PR$) and the FOV is given by Equation (1).

$$\mathrm{FOV}=2{\tan }^{-1}\left(\frac{PR}{2\left(f/\rho \right)}\right)$$

(1)

where FOV is the field of view of the star sensor, $f$ is its focal length, $\rho$ is the pixel size, and $PR$ is the maximum pixel distance.

The FOV is oriented such that all stars in the FOV are aligned on the nearest neighbor outside a certain radius. The pixel coordinates of stars in the oriented FOV, except the central star, constitute a coordinate column stored as the template corresponding to the star ID in the template database, which is given by Equation (2).

$$S{P}_{ID}=\left[\left(x_i,y_i\right)\right],i=1,2,\cdots ,n_{ID}$$

(2)

where $x_i,y_i$ are the pixel coordinates of other stars in the oriented FOV and $n_{ID}$ is the number of stars in the FOV, excluding the central star.

3.3. Registration between a Captured Image and the Template

There are three steps in the registration between a captured image and the template.

Step One: The reference star ${\mathrm{S}}_{ref}$ is selected from image $\mathrm{I}$ for identification based on the criterion that the maximum number of stars in the FOV should be preserved after relocating ${\mathrm{S}}_{ref}$ and part of the surrounding sky, such that ${\mathrm{S}}_{ref}$ lies at the center of the FOV, and this process is given by Equation (3).

$${\mathrm{S}}_{ref}=\arg \underset{S_i\in I}{\max }card\left\{sta{r}^{\prime }\left|d\left(sta{r}^{\prime },S_i\right)<PR\right.\right\}$$

(3)

where $S_i$ is one of the star points extracted from image $\mathrm{I}$, with $sta{r}^{\prime }$ being any star points in the image except $S_i$, $d\left(sta{r}^{\prime },S_i\right)$ being the distance between $sta{r}^{\prime }$ and $S_i$, and $card$ calculating the number of set elements.

Step Two: The nearest-neighbor star set is constructed. Star positioning errors and the distances from stars to the edge of the FOV are considered to design the flexible criteria for the construction of the closest-neighbor star set. Specifically, stars are added into the nearest-neighbor star set $\mathrm{nbs}$ when their distance to $S_{ref}$ is within the range of $\left[d{r}_{\min },d{r}_{\min }+d\right]$, where $d{r}_{\min }$ is the minimum distance from stars whose distance to $S_{ref}$ is greater than the threshold $b$ but smaller than the shortest distance from $S_{ref}$ to the edges of the FOV and $d$ is the tolerance for star positioning errors. The nearest-neighbor star set is used to align the FOV. The goal of imposing the threshold $b$ is to ensure that any member of the nearest-neighbor star set is not so close to $S_{ref}$ that a small positioning error of any member star will introduce large positioning errors to other stars upon aligning the FOV. Note that $b$ needs tuning, and a parameter analysis was conducted to determine its value in simulation. The goal of imposing the threshold $bo$ is to ensure that all members of the nearest-neighbor star set lie in the FOV centered on $S_{ref}$. The threshold $bo$ is determined as the shortest distance from other stars except $S_{ref}$ to the boundaries of the FOV. The soft criteria can be given by Equation (4).

$$\begin{array}{l}\mathit{n}\mathit{b}\mathit{s}=\left\{sta{r}^{\prime }\left|d{r}_{\min }\le d\left(sta{r}^{\prime },S_{ref}\right)\le d{r}_{\min }+d\right.\right\}\\ d{r}_{\min }=\min \left\{d\left(sta{r}^{\prime },S_{ref}\right)\left|b<d\left(sta{r}^{\prime },S_{ref}\right)<bo\right.\right\}\end{array}$$

(4)

where $sta{r}^{\prime }$ is any star point in the image except $S_{ref}$, with $bo$ being the shortest distance from $sta{r}^{\prime }$ to the boundaries of the FOV.

Step Three: The FOV is translated and rotated to align with the template. First, $S_{ref}$ and the surrounding FOV are translated such that $S_{ref}$ lies at the center of the FOV. Second, the stars are rotated and aligned on the nearest-neighbor star set $\mathit{nbs}$. Third, the pixel coordinate features of the image are extracted using the stars in $sta{r}^{\prime }$ remaining in the FOV except $S_{ref}$, and this process is given by Equation (5).

$$IP=\left[\left({x^{\prime }}_i,{y^{\prime }}_i\right)\right],i=1,2,\cdots ,n_{ref}$$

(5)

where ${x^{\prime }}_i,{y^{\prime }}_i$ are the pixel coordinates of the stars in $sta{r}^{\prime }$ remaining in the FOV after registration and $n_{ref}$ is the number of stars in $sta{r}^{\prime }$.

3.4. Shortlisting Similarity

3.4.1. Shortest Distance Transformation

The shortest distance transformation is a common mathematical transformation in the field of image processing. In this paper, it is defined as follows. The entire set $\mathsf{\Omega }$ consists of all pixels in an image, and for each pixel point $p$ in it, the shortest distance can be defined by a certain subset ${\mathsf{\Omega }}^c$ consisting of the pixel points of the stars. This definition is given by Equation (6).

$$D\left(p\right)=\min \left\{d\left(p,q\right)|q\in {\mathsf{\Omega }}^c\right\}$$

(6)

where $D\left(p\right)$ is the shortest distance of point $p$ with respect to the star image and $q$ represents the pixel point in which a star is located in the image. In this case, the Euclidean distance in pixels is given by Equation (7).

$$d\left(p,q\right)=\sqrt{{\left(p_x-q_x\right)}^2+{\left(p_y-q_y\right)}^2}$$

(7)

The shortest distance transformation is preferred because of its invariance to translation and rotation.

3.4.2. Similarity

In this paper, the shortest distance transformation is used to calculate the similarity of the image to every template. We define the subset ${\mathsf{\Omega }}^c$ consisting of stars in the image and calculate the shortest distance transformation of every star $sta{r}_i$ in one template $S{P}_{ID}$ of the template database with respect to ${\mathsf{\Omega }}^c$ as $D{T}_{ID}=\left\{d{m}_i|d{m}_i=D\left(sta{r}_i\right),i=1,2,\cdots ,n_{ID}\right\}$. $D{T}_{ID}$ is sorted in ascending order to obtain $D{T}_{ID}^{sorted}=\left[d{m}_j\right],j=1,2,\cdots ,n_{ID}$. Then, the similarity between the image and template can be defined as Equation (8).

$$s{m}_{ID}=-{\displaystyle \sum _{j=1}^{n_{sm}}d{m}_j}$$

(8)

where

$$n_{sm}=\min \left(n_{ref},n_{ID}\right)$$

(9)

Note that not only the distance but also the information of the angle between stars are hidden in the distance map, which is actually another form of grid.

3.4.3. Local Scope

The similarity defined in Equation (8) will encounter difficulties when facing false or missing stars because the shortest distance transformation is related to the global subset ${\mathsf{\Omega }}^c$, which means that any changes in ${\mathsf{\Omega }}^c$ will interfere with the calculation of the similarity between the image and template. Therefore, a local scope is defined to improve the robustness of the shortest distance transformation, as shown in Figure 7. Figure 7 shows how the improved local scope similarity is calculated: First, the similarity map is calculated based on the shortest distance transformation; then, the local scope mask with $K=5$ is used to mask the similarity map to achieve the improved local scope similarity. The local scope radius denoted as $K$ is used to obtain a mask with specific size, and star points whose max coordinate difference is greater than the scope radius $K$ are eliminated.

In Figure 7, an example with $K$ equal to 1 is used to illustrate the local scope and improved local scope similarity. A portion of the similarity map calculated by Equation (8) is masked by the local scope with $K$. Note that $K$ is a tuning parameter and takes value of 5 at last. As a result, star points in blue are counted in the improved local scope similarity, while star points in yellow are ignored. The improved local scope similarity can be defined as

$$ls{m}_{ID}=-{\displaystyle \sum _{j=1}^{n_{sm}}d{m}_j\cdot local\left(d{m}_j,K\right)}$$

(10)

$$local\left(d{m}_j,K\right)=\left\{\begin{array}{c}1,d{m}_j\le K\\ 0,d{m}_j>K\end{array}\right.$$

(11)

3.5. Fast Validation

The improved local scope similarity is used in the first step of matching, in which embedded fast validation is designed. Fast validation accelerates the overall identification process because a star passing the fast validation can be directly output as an identification outcome without requiring the second matching step.

Fast validation is based on the principle that the distances between the stars in an image and the corresponding stars in the correctly identified template are small. Therefore, one type of verification method determines whether the number of close stars whose shortest distance is less than a certain threshold account for greater than a certain proportion of the total [50]. If so, the recognition is validated. Otherwise, the recognition is rejected. This kind of method is defined by Equation (12).

$$V_{rate}=\frac{n_{close}}{n_{sm}}$$

(12)

$$n_{close}={\displaystyle \sum _{j=1}^{n_{sm}}local\left(d{m}_j,K\right)}$$

(13)

However, this method has a problem that distortion in the gnomonic projection of a patch of spherical surface onto the plane surface of the imager causes positioning errors for stars in the nearest-neighbor star set $\mathit{n}\mathit{b}\mathit{s}$. Because the registration process will rotate the image according to the vector between the reference star and the closest-neighbor star, the positioning errors of the nearest-neighbor star will be transferred to the stars other than the reference star and the nearest-neighbor star. Specifically, the registration process will amplify this kind of position error proportional to the distance from the reference star to the other stars, which will interfere with the described validation. As shown in Figure 8, the practical closest-neighbor star position PN has a position error ns1 with respect to the ideal closest-neighbor star position IN. Then position error ns1 will introduce a position error ns2 to another star PS with its ideal position IS during the registration process. b is the distance between IN and RS. l is the distance between IS and RS. There is a relationship of similar triangles as

$$\frac{ns1}{b}=\frac{ns2}{l}$$

(14)

where ns1, ns2, b, and l are in pixels. For the registered matching template, the shortest distance introduced by these positioning errors and the distance from the star to the center of the FOV can fit a line with a small but non-zero fitting residual because of image plane distortion.

Based on the idea described above, we developed a method for fast validation. The shortest distance of stars $\left[d{m}_i\right],i=1,2,\cdots ,n_{sm}$ and their distance to the center of the FOV $\left[d\left(sta{r}_i,S_{ref}\right)\right],i=1,2,\cdots ,n_{sm}$ are used to fit the line $Lf\left(\cdot \right)$. If the mean square error of line fitting $MR$ defined by Equation (15) is smaller than a tuning threshold $th1$, the recognition is validated, and a star with maximum shortlisting similarity is directly output. Otherwise, the second matching step will be executed. We will show that these validation criteria can help provide a clear distinction between correct and incorrect identifications with a proper $th1$ value in Section 4.2. Note that $th1$ needs tuning, and a parameter analysis was conducted to determine its value in simulation.

$$MR=\sqrt{{\displaystyle \sum _{i=1}^{n_{sm}}{\left(d{m}_i-Lf\left(d\left(sta{r}_i,S_{ref}\right)\right)\right)}^2}/n_{sm}}$$

(15)

3.6. Decisive Similarity

Decisive similarity $DSM$ is designed to match the shortlisted templates that do not pass fast validation with the image. As shown in Equation (16), both the fraction of close stars $V_{rate}$ and the specific shortest distance $s{m}_{ID}$ are taken into account. To avoid the selection of templates containing much fewer close stars, which is obviously not the desired outcome, the fraction of close stars $V_{rate}$ is given a much greater weight. Note that $V_{rate}$ can be calculated by Equation (12).

$$\begin{array}{c}DSM=w_1\ast V_{rate}+w_2\ast s{m}_{ID}\\ w_1\gg w_2\end{array}$$

(16)

where $w_1,w_2$ are the weights for $V_{rate}$ and $s{m}_{ID}$, with fine-tuned $w_1=1$ and $w_2={10}^{-5}$ values.

3.7. Final Validation

A star sensor needs to avoid false recognitions as much as possible; thus, a rejection mechanism is required. A correctly recognized pattern will include a large percentage of close stars, and the percentage of close stars $V_{rate}$ can be calculated by Equation (12). In this paper, final validation determines whether the percentage of close stars $V_{rate}$ is less than a tuning threshold $th2$ [50]. If so, the recognition is validated. Otherwise, the recognition is rejected. Note that $th2$ needs tuning, and a parameter analysis was conducted to determine its value in simulation.

3.8. Overall Framework

In conclusion, a schematic overview of the proposed algorithm is shown in Figure 9. A two-step matching framework with fast validation embedded facilitates identification, while shortlisting similarity based on the distance transformation and local spatial information offers sufficient robustness. The whole framework not only improves recognition reliability but also ensures recognition efficiency. Note that the designed two-step validation mechanism can directly refuse an image without the need to repeatedly identify other stars.

4. Simulation Results and Analysis

4.1. Simulation Conditions

To thoroughly test the proposed algorithm, Monte Carlo simulations were conducted. A total of 1,000,000 images with the simulated star sensor’s center of FOV evenly distributed on the celestial sphere were created, as shown in Figure 10, to form the star image test set used in various subsequent tests. Methods of distributing points evenly on a sphere have been profoundly studied [56]. We adopted a tool provided by Anton Semechko to evenly produce points on the celestial sphere [57]. There were 4956 stars in the test on the celestial sphere.

4.2. Parameter Analysis

First, the effectiveness of the proposed method for selecting a reference star was tested. As a result, the proposed method for selecting a reference star for identification enabled the star point preservation rate to increase from 87.17% to 90.31%, providing more abundant and reliable information for subsequent matching.

Second, a parameter analysis was conducted to determine the values of the parameters in the proposed algorithm, which included the radius threshold $b$, position tolerance scale $d$, number of shortlists $N$, fast validation threshold $th1$ and final validation threshold $th2$.

The average number of stars in the closest-neighbor star set and the choice accuracy of closest-neighbor stars under different radius thresholds $b$ and different position tolerance scales $d$ were studied, as shown in Figure 11 and Figure 12, respectively. The former determined the computational complexity, while the latter determined the upper limit of the subsequent recognition accuracy. It can be seen that parameter $b$ had little effect on the average number of stars but parameter $d$ had an effect. Both parameter $b$ and parameter $d$ had effects on the choice accuracy of the closest-neighbor star. We set $b$ as 24 pixels and $d$ as 2 pixels, such that the choice accuracy of closest-neighbor stars was almost the highest and robust to various noises and the number of stars in the closest-neighbor star set was relatively small.

As shown in Figure 13, the probability of shortlisting correctly identified stars under different numbers of shortlisted stars $N$ was also analyzed. We set $N$ as 90, such that the probability of shortlisting correctly identified stars was relatively large, with a moderate computational complexity.

Both the value of the fast validation threshold th1 and the value of the final validation threshold th2 need to be optimized. To examine how the fast validation and final validation criteria separate correct identifications from incorrect identifications, we constructed histograms of both criteria. The criteria are depicted on the horizontal axis, and the vertical axes indicate the numbers of correct and incorrect identifications.

As seen from Figure 14 and Figure 15, the fast validation and final validation criteria clearly separate correct cases from incorrect cases and correctly identify most cases. The principle of the value optimization of th1 and th2 is to separate correct recognitions from incorrect recognitions and to ensure robustness as much as possible. In this case, we set th1 to 23 pixels and th2 to 75%, such that correct and incorrect determinations were clearly separated by the criteria. It was shown that the metrics used in fast validation and final validation could well-separate incorrect determinations from correct determinations, also facilitating the selection of th1 and th2.

4.3. Ideal Case

We compared highly reliable geometric algorithms (including the geometric voting algorithm (GMV) [15] and pyramid algorithm [19]) and pattern recognition algorithms (including the search tree-based algorithm (STOD) [37] and polestar algorithm [24]) with our proposed algorithm.

In an ideal scenario, no positioning errors or interfering star exist in the simulated image. However, star identification methods still face the problem of losing stars during the registration process. The results in

Table 1. Benchmarking of star identification methods—ideal case.

Method	Identification Accuracy (%)	Run Time (s)
GMV [15]	94.3	0.567
STOD [34]	90.3	0.21
Polestar [24]	97.86	0.386
Pyramid [19]	99.98	0.41
Proposed	100	0.52

show that the proposed algorithm outperformed the other methods in identification accuracy in the test environment. However, the speed of the proposed method was moderate. We therefore began looking for a way to eliminate the need for explicit translation and rotation of the image and to construct a more efficient template database. The test for the robustness of star identification in scenarios including positioning noise or interfering stars in the simulated images is presented later in this section. Both the identification rate and misidentification rate are key indicators of robustness, although a filter is also used in attitude determination to reject incorrect attitude solutions resulting from misidentifications. Example benchmarking results of other methods are provided by Samirbhai [43].

4.4. Sensitivity to Star Positioning Errors

Star point information is obtained by a star point extraction algorithm, which introduces positioning errors or noise into the star points. Existing star point extraction algorithms can reach an accuracy level of approximately 0.1 pixels. In addition, defects in an image sensor and optical system may also cause star positioning errors. In particular, low-quality components in low-cost cameras may cause large positioning errors.

To test the sensitivity of the proposed algorithm to positioning errors, we added Gaussian noise to the test image set and set the mean noise value to 0 and the standard deviation to 1–10 pixels, corresponding to 50–500 arcseconds.

The robustness was evaluated by the identification accuracy, which was calculated as the number of correct identifications divided by the total number of tests, and the misidentification rate, which was calculated as the number of misidentifications divided by the total number of tests. In addition, the acceptance accuracy was calculated as the number of correct identifications divided by the sum of correct identifications and misidentifications.

As shown in Figure 16, the proposed algorithm maintained an approximately 100% acceptance accuracy with the introduction of 1–10-pixel positioning errors. When the positioning error was 2 pixels, the identification accuracy of the algorithm was still greater than 90%. Even when the positioning error was 10 pixels, which far exceeded practical values, the accuracy and reliability of the proposed algorithm were verified and confirmed.

Compared with the other algorithms, the proposed algorithm had a strong advantage in robustness to star point positioning errors, as shown in Figure 17 and Figure 18. The proposed algorithm maintained the highest identification accuracy and rejected almost all misidentifications.

It is important to note that in Figure 18, the misidentification rate of the proposed algorithm remained the lowest, with a value equal to zero. In addition, the misidentification rates of the geometric methods, including the GMV and pyramid methods, were much higher than those of the other pattern recognition methods.

The strong star positioning error robustness of the proposed algorithm is due to its designed inclusion of the global and local features of star point distributions and the comprehensive utilization of the geometric information in star images.

4.5. Sensitivity to Missing Stars

Due to registration errors of the maximum sensitivity and sensor component failure, the camera may lose some stars that could have been captured in the FOV. To test the robustness of the proposed algorithm to the problem of missing stars in the FOV, we randomly discarded 1–10 stars from the FOV of each image in the test set.

As shown in Figure 19, when two stars were lost, the acceptance accuracy remained at almost 100%. When 10 stars were lost, the acceptance accuracy dropped by 5.24%. When the number of missing stars was less than three, although the number of rejections increased because of the lack of star points in the FOV, the total identification accuracy remained over 80%. Therefore, these results proved that the proposed algorithm is robust to missing star problems.

Compared with the other algorithms, the proposed algorithm had a strong advantage in robustness to missing stars, as shown in Figure 20 and Figure 21. Figure 21 shows that the misidentification rate of the proposed algorithm was relatively low. Similarly, the misidentification rates of the geometric methods were higher than those of the other pattern recognition methods.

However, compared with the robustness to positioning errors and false stars, the recognition accuracy was the lowest in the case of missing stars. The reason for this result is that the developed method also uses the closest neighbor to register an image, and this process can undergo interference when the correct nearest-neighbor star is missing. At the cost of computational complexity, the registration process can be improved to enhance the algorithm’s robustness against missing stars.

4.6. Sensitivity to False Stars

False stars are star points appearing in the FOV for which a match cannot be found in the template database. Reasons for the generation of false stars can be divided into five categories as follows:

(1)

Natural targets (such as planets and natural satellites) and manned objects (such as artificial satellites and space debris) may pass through the camera’s FOV, forming false stars. Due to the reflection of sun rays by the object, a false star produced in this case may have high brightness. Some planets, such as Uranus and Neptune, having visual magnitudes between 6 and 8, are very dim objects, near or beyond the detection threshold of the most wide field of view star trackers.

(2)

Various noise sources in the camera, such as flaws in the lens and detector components, may produce false stars. This situation can be controlled by using high-quality components but involves a high cost.

(3)

The complex radiation environment of the universe and the impact of high-energy particles may also produce false stars in the camera’s FOV.

(4)

Sensitivity calibration errors in the camera detector and the absence of variable or real stars in the onboard star tracker catalog may also cause the appearance of false stars.

(5)

Novas, which are stars that temporarily increase in brightness by many orders of magnitude, may also cause the appearance of false stars.

To test the sensitivity of the proposed algorithm to false stars, we added 1–10 false stars with random positions to each test image generated by a Gaussian distribution into the FOV.

As shown in Figure 22, the proposed algorithm maintained approximately 100% acceptance accuracy and identification accuracy upon the random introduction of 1–10 false stars. Therefore, the results proved that the proposed algorithm is extremely insensitive to false stars. Compared with the other algorithms, the proposed algorithm also had a strong advantage in this evaluation, as shown in Figure 23 and Figure 24.

5. Discussion

Providing an incorrect solution is much worse than not providing an identification solution, since the attitude solution provided by the star sensor based on an incorrect solution can endanger a spacecraft if not properly filtered by the attitude determination process.

It is encouraging that the introduction of false stars caused very few misidentifications by the proposed algorithm. The results clearly showed that false stars can hardly pass fast validation, in which the line-fitting residual is checked, or final validation, in which the percentage of close stars is checked. Our originally proposed masked distance map and embedded validation mechanism not only accelerate recognition but also reduce the misidentification rate in the face of various errors and noise. However, there are also disadvantages of the proposed method. Missing stars will significantly decrease accuracy because missing stars will cause significant damage to the pattern of the masked distance map. Additionally, the efficiency of the proposed method can be improved. We are looking for a way to eliminate the need for the explicit translation and rotation of the image and to construct a more efficient template database. Above all, in the ideal case, the proposed method achieved the best results. This is because the proposed method can improve recognition accuracy with a small increase in computing time through reasonable matching feature design and embedded verification. When facing star position errors, the proposed method has the highest robustness, and overall, the robustness of the pattern recognition method was found to be lower than that of the geometric method. This is because the absolute constraint of pattern designed by traditional pattern matching method on star point position is weaker and softer than that of the geometric method. For the missing star problem, the polestar method has achieved the best score, followed by our method. This is because the pattern of the polestar method is specially designed for the star missing problem and is fundamentally robust for the star shortage problem. Generally, the robustness of the pattern matching method was found to be higher than that of the geometric method. This is because the similarity comparison of the geometric method is based on hard criteria. The missing star problem will greatly damage the geometric relationship between stars, such as edges and angles. When facing the problem of fake stars, our method shows very high performance, also because the feature of masked distance map we designed is very robust to fake stars; this also leads to our high acceptance accuracy, and the embedded verification makes our method’s mis-identification rate very low. GMV achieved the worst result because its features were obtained not with a robust design but only with a voting screening design. Although the pyramid method is a geometric method, it also shows good robustness because it also considers the problem of fake stars in the geometric feature design.

6. Conclusions

The algorithm described here provides robust star identification, even with the presence of star positioning errors, false stars, and missing stars, as proven by the simulation results. The algorithm favorably compares with existing star identification methods in terms of accuracy and performance. The proposed algorithm with high robustness to various kinds of star noise could play a role in deep space missions such as asteroid exploration missions, in which star sensors inevitably face dangerous environments that include uncertainty. Additionally, the proposed algorithm will help reduce the requirements of optical systems of star sensors and thus lower the cost of related equipment, which is favorable for small satellites produced with limited budgets. The potential of distance map in application to star identification has not been fully tapped. Future work will include a combination of distance map and neural network. We look forward to test the proposed method in a CubeSat mission.