Hierarchical Superpixel Segmentation for PolSAR Images Based on the Boruvka Algorithm
Abstract
:1. Introduction
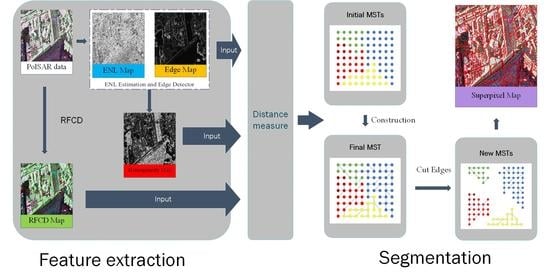
2. Methodology
2.1. PolSAR Data
2.1.1. Wishart Distribution and Wishart Distance
2.1.2. Refined Five-Component Decomposition
2.2. Distance Measure Construction
2.3. Hierarchical Segmentation
2.4. Implementation Details
| Algorithm 1. Superpixel generation for the PolSAR image. |
| Input: The original PolSAR image and the predetermined number of superpixels K. |
| Output: The average image of the segmentation results. |
| 1. Each pixel is initialized as an MST, and the RFCD feature, edge map, ENL map, and Homogeneity map are calculated. |
| 2. Traverse the table of edges to find the tree closest to each tree by calculating weight using (19), and connect them, obviously, the number of trees is halved. |
| 3. Repeat step 2 until there is one tree left, which is the final MST. |
| 4. Sort the edges in each MST according to the weight in descending order. |
| 5. Cut off the edge with largest weight to obtain new MSTs. |
| 6. If the number of MSTs is equal to K, average the pixel value in each MST. Or repeat steps 4 and 5. |
| 7. Output the average image of the segmentation results. |
3. Experimental Results and Analysis
3.1. Dataset Description and Parameter Setting
3.2. Quantitative Evaluation Metrics
3.3. Superpixel Segmentation Results of ESAR Data
3.4. Superpixel Segmentation Results of AIRSAR Data
4. Discussion
4.1. Multi-Scale Comparison
4.2. Contribution Analysis of the Distances Measure
4.3. Computational Complexity and Run Time
4.4. Analysis of the Limitation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, S.J.; Luo, H.; Shi, Q. Active Ensemble Deep Learning for Polarimetric Synthetic Aperture Radar Image Classification. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1580–1584. [Google Scholar] [CrossRef]
- Imani, M. Median-mean line based collaborative representation for PolSAR terrain classification. Egypt. J. Remote Sens. Space Sci. 2022, 25, 281–288. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, M.; Zhang, P.; Tan, X.; Song, W. Unsupervised Complex-Valued Sparse Feature Learning for PolSAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Ni, J.; Xiang, D.; Lin, Z.; López-Martínez, C.; Hu, W.; Zhang, F. DNN-Based PolSAR Image Classification on Noisy Labels. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3697–3713. [Google Scholar] [CrossRef]
- Cui, X.C.; Su, Y.; Chen, S.W. A Saliency Detector for Polarimetric SAR Ship Detection Using Similarity Test. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3423–3433. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, F.; Xiang, D.; Yin, Q.; Zhou, Y. PolSAR Image Classification with Multiscale Superpixel-Based Graph Convolutional Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, W.; Quan, S.; Yang, H.; Xiong, H.; Zhang, Z.; Yu, W. Region-Based Polarimetric Covariance Difference Matrix for PolSAR Ship Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Zhang, T.; Du, Y.; Yang, Z.; Quan, S.; Liu, T.; Xue, F.; Chen, Z.; Yang, J. PolSAR Ship Detection Using the Superpixel-Based Neighborhood Polarimetric Covariance Matrices. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef]
- Jianbo, S.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Li, Z.; Huang, B. Linear Spectral Clustering Superpixel. IEEE Trans. Image Processing 2017, 26, 3317–3330. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Qin, F.; Guo, J.; Lang, F. Superpixel Segmentation for Polarimetric SAR Imagery Using Local Iterative Clustering. IEEE Geosci. Remote Sens. Lett. 2015, 12, 13–17. [Google Scholar] [CrossRef]
- Song, H.; Yang, W.; Bai, Y.; Xu, X. Unsupervised classification of polarimetric SAR imagery using large-scale spectral clustering with spatial constraints. Int. J. Remote Sens. 2015, 36, 2816–2830. [Google Scholar] [CrossRef]
- Feng, J.; Cao, Z.; Pi, Y. Polarimetric Contextual Classification of PolSAR Images Using Sparse Representation and Superpixels. Remote Sens. 2014, 6, 7158–7181. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, Q.; Yang, S.; Liu, X. Superpixel-Based Classification Using K Distribution and Spatial Context for Polarimetric SAR Images. Remote Sens. 2016, 8, 619. [Google Scholar] [CrossRef]
- Hou, B.; Yang, C.; Ren, B.; Jiao, L. Decomposition-Feature-Iterative-Clustering-Based Superpixel Segmentation for PolSAR Image Classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1239–1243. [Google Scholar] [CrossRef]
- Zhang, L.; Han, C.; Cheng, Y. Improved SLIC superpixel generation algorithm and its application in polarimetric SAR images classification. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4578–4581. [Google Scholar]
- Xiang, D.; Ban, Y.; Wang, W.; Su, Y. Adaptive Superpixel Generation for Polarimetric SAR Images With Local Iterative Clustering and SIRV Model. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3115–3131. [Google Scholar] [CrossRef]
- Lin, H.; Bao, J.; Yin, J.; Yang, J. Superpixel Segmentation with Boundary Constraints for Polarimetric SAR Images. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6195–6198. [Google Scholar]
- Quan, S.; Xiang, D.; Wang, W.; Xiong, B.; Kuang, G. Scattering Feature-Driven Superpixel Segmentation for Polarimetric SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2173–2183. [Google Scholar] [CrossRef]
- Xu, X.; Zou, B.; Zhang, L. Polarimetric Semivariogram-Based Spatial Scale Selection for PolSAR Image Segmentation with Mean-Shift Algorithm. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1239–1243. [Google Scholar] [CrossRef]
- Lang, F.; Yang, J.; Yan, S.; Qin, F. Superpixel Segmentation of Polarimetric Synthetic Aperture Radar (SAR) Images Based on Generalized Mean Shift. Remote Sens. 2018, 10, 1592. [Google Scholar] [CrossRef]
- Liu, B.; Hu, H.; Wang, H.; Wang, K.; Liu, X.; Yu, W. Superpixel-Based Classification With an Adaptive Number of Classes for Polarimetric SAR Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 907–924. [Google Scholar] [CrossRef]
- Xu, X.; Zou, B.; Zhang, L. Object-based Normalized-Cuts for High-Resolution Polsar Image Segmentation. In Proceedings of the 2019 SAR in Big Data Era (BIGSARDATA), Beijing, China, 5–6 August 2019; pp. 1–4. [Google Scholar]
- Wang, W.; Xiang, D.; Ban, Y.; Zhang, J.; Wan, J. Superpixel Segmentation of Polarimetric SAR Images Based on Integrated Distance Measure and Entropy Rate Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4045–4058. [Google Scholar] [CrossRef]
- Lin, W.; Li, Y. Parallel Regional Segmentation Method of High-Resolution Remote Sensing Image Based on Minimum Spanning Tree. Remote Sens. 2020, 12, 783. [Google Scholar] [CrossRef]
- Wei, X.; Yang, Q.; Gong, Y.; Ahuja, N.; Yang, M.H. Superpixel Hierarchy. IEEE Trans Image Process 2018, 27, 4838–4849. [Google Scholar] [CrossRef]
- Zhang, W.; Xiang, D.; Su, Y. Fast Multiscale Superpixel Segmentation for SAR Imagery. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, W.; Xiang, D.; Ban, Y.; Zhang, J.; Wan, J. Enhanced edge detection for polarimetric SAR images using a directional span-driven adaptive window. Int. J. Remote Sens. 2018, 39, 6340–6357. [Google Scholar] [CrossRef]
- Xiang, D.; Ban, Y.; Wang, W.; Tang, T.; Su, Y. Edge Detector for Polarimetric SAR Images Using SIRV Model and Gauss-Shaped Filter. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1661–1665. [Google Scholar] [CrossRef]
- Quan, S.; Xiong, B.; Xiang, D.; Hu, C.; Kuang, G. Scattering Characterization of Obliquely Oriented Buildings from PolSAR Data Using Eigenvalue-Related Model. Remote Sens. 2019, 11, 581. [Google Scholar] [CrossRef]
- Wang, W.; Zhai, Q.; Ban, Y.; Zhang, J.; Wan, J. PolSAR image segmentation based on hierarchical region merging and segment refinement with WMRF model. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4574–4577. [Google Scholar]
- Goodman, N.R. Statistical Analysis Based on a Certain Multivariate Complex Gaussian Distribution (An Introduction). Ann. Math. Stat. 1963, 34, 152–177. [Google Scholar] [CrossRef]
- Conradsen, K.; Nielsen, A.A.; Schou, J.; Skriver, H. A test statistic in the complex wishart distribution and its application to change detection in polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 4–19. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Quan, S.; Xiong, B.; Xiang, D.; Zhao, L.; Zhang, S.; Kuang, G. Eigenvalue-Based Urban Area Extraction Using Polarimetric SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 458–471. [Google Scholar] [CrossRef]
- Yu, W.; Wang, Y.; Liu, H.; He, J. Superpixel-Based CFAR Target Detection for High-Resolution SAR Images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 730–734. [Google Scholar] [CrossRef]
- Lang, F.; Yang, J.; Li, D. Adaptive-Window Polarimetric SAR Image Speckle Filtering Based on a Homogeneity Measurement. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5435–5446. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Z.; Liu, X.; Yu, W. Edge Extraction for Polarimetric SAR Images Using Degenerate Filter with Weighted Maximum Likelihood Estimation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2140–2144. [Google Scholar] [CrossRef]
- Anfinsen, S.N.; Doulgeris, A.P.; Eltoft, T. Estimation of the Equivalent Number of Looks in Polarimetric Synthetic Aperture Radar Imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3795–3809. [Google Scholar] [CrossRef]













| Methods | Datasets | Number of Superpixels | Average | |||
|---|---|---|---|---|---|---|
| 500 | 1000 | 2500 | 5000 | |||
| The proposed method | ESAR | 3.912 | 3.931 | 3.896 | 3.895 | 3.909 |
| AIRSAR | 1.068 | 1.066 | 1.073 | 1.072 | 1.070 | |
| Pol-ASLIC | ESAR | 12.709 | 15.292 | 10.297 | 15.487 | 13.446 |
| AIRSAR | 12.868 | 21.523 | 17.049 | 13.832 | 16.318 | |
| Pol-ERM | ESAR | 12.344 | 14.016 | 20.578 | 31.266 | 19.551 |
| AIRSAR | 4.281 | 5.125 | 7.313 | 9.328 | 6.512 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, J.; Wang, W.; Quan, S.; Zhan, R.; Zhang, J. Hierarchical Superpixel Segmentation for PolSAR Images Based on the Boruvka Algorithm. Remote Sens. 2022, 14, 4721. https://doi.org/10.3390/rs14194721
Deng J, Wang W, Quan S, Zhan R, Zhang J. Hierarchical Superpixel Segmentation for PolSAR Images Based on the Boruvka Algorithm. Remote Sensing. 2022; 14(19):4721. https://doi.org/10.3390/rs14194721
Chicago/Turabian StyleDeng, Jie, Wei Wang, Sinong Quan, Ronghui Zhan, and Jun Zhang. 2022. "Hierarchical Superpixel Segmentation for PolSAR Images Based on the Boruvka Algorithm" Remote Sensing 14, no. 19: 4721. https://doi.org/10.3390/rs14194721
APA StyleDeng, J., Wang, W., Quan, S., Zhan, R., & Zhang, J. (2022). Hierarchical Superpixel Segmentation for PolSAR Images Based on the Boruvka Algorithm. Remote Sensing, 14(19), 4721. https://doi.org/10.3390/rs14194721