VMD–WT-Based Method for Extracting On-the-Fly GNSS Tide Level and Its Realization

Abstract

In this paper, a method for extracting the on-the-fly (OTF) GNSS tide level was designed by combining variational modal decomposition (VMD) and a wavelet thresholding (WT) method to improve the extraction accuracy of the OTF GNSS tide level. First, the energy difference ratio method was used to determine the number of layers for the VMD. Subsequently, the VMD performed a second decomposition of the IMF1 obtained from the first VMD to achieve an efficient separation of signal and noise. The normalized cross-correlation coefficient (NCC) was applied to determine the number of layers for the WT method. Finally, experimental results showed that the VMD–WT method outperformed the other seven filtering methods in three metrics: maximum error, the root-mean-square error (RMSE), and error distribution. Therefore, the VMD–WT method was able to extract extremely accurate on-the-fly GNSS tide level and additionally obtain more accurate bathymetry data after tidal correction of the bathymetry data.

1. Introduction

An indispensable step in data processing is obtaining the tide level data of a survey area synchronously and completing a tide level correction in the process of using sonar to measure the marine topography. However, there are numerous unfavorable factors such as the special care, time-intensiveness, site selection, and interpolation error of the tide level model for tide level observation through the traditional measuring method of water gauge and tide gauge [1,2]. The on-the-fly GNSS tide measurement is an efficient and postprocessed tide measurement method, which has been widely applied.

The concept of the GPS tide measurement was first proposed in the 1990s. DeLoach [3], Shannon et al. [4], Ngagipar et al. [5], Salleh et al. [6] successfully researched shipborne or buoy GPS tide measurement. Experimental results revealed that the accuracy of the GPS tide measurement could reach centimeter level [3,4,5,6]. Zhao et al. [7,8,9,10] of Wuhan University in China performed systematic research on OTF GNSS tide measurement using GPS RTK/PPK/PPP positioning technology. They revealed that the GPS RTK/PPK/PPP tide measurement results maintained a high consistency with the tide level of the tide station, and the tide measurement accuracy reached the centimeter level, providing significant practical value [10].

The sea surface geodetic height sequence is a complex and comprehensive signal, and the filtering method of the sea surface geodetic height sequence still has many limitations. The threshold filtering method requires multiple calculations to determine the wave period and involves cumbersome calculations [11]. Comparing three filtering methods, that is, the window method for FIR filter design, a Butterworth low-pass filter, and low-pass filtering by FFT convolution, Ma et al. [12] demonstrated that the low-pass filter based on FFT exhibited a greater accuracy in extracting the tide level. However, the FFT method had the issue of an empirical setting of the cut-off period, and the accuracy of the cut-off period directly affected the accuracy of the tide level extraction. Yang et al. [13] employed a wavelet transform forced noise elimination method to filter out the high-frequency noise in the sea surface geodetic height sequence. The wavelet transform has the excellent characteristics of a multiscale refinement analysis. However, the effect of denoising depends on the selection of the wavelet basis function since only a fixed wavelet basis function can be selected to analyze the signal, leading to a lack of adaptability of the wavelet transform [14,15]. Pan et al. [16] applied the empirical mode decomposition (EMD) method to analyze the nonstationary characteristics of the D₁ tides, the D₂ tides, and subtidal oscillations induced by changing river flow, while there was the complication of mode aliasing, a poor noise immunity, and an endpoint effect. Pan et al. [17] applied a continuous wavelet transform to the 7-year data from Vancouver to extract the diurnal (D1) species amplitude and semidiurnal (D2) species amplitude and achieved excellent results. Devlin et al. [18] used the ensemble empirical mode decomposition (EEMD) method to analyze tidal amplitudes and sea level at multiple frequency bands. However, the mode aliasing phenomenon still existed in the results of the EEMD when dealing with river tides. In 2014, Konstantin et al. [19] proposed the variational modal decomposition (VMD), a nonrecursive signal processing method performing adaptive decomposition according to the characteristics of the signal itself and the latest development of EMD. It had the characteristics of suppressing high-frequency noise and was suitable for processing nonperiodic and nonstationary signals [20]. In 2021, Gan et al. [21] first applied the VMD method to a harmonic analysis of nonstationary river tides observed by fixed tide gauges; their research proved that the VMD method strictly divided different tidal species into different modes, and thus avoided mode aliasing.

In this paper, the VMD algorithm is introduced into OTF GNSS tide measurement. By combining the advantages of the VMD algorithm (adaptive decomposition and suppression of high-frequency noise) with the optimal approximation characteristics of the wavelet transform to the signal, a filtering method combining VMD and wavelet thresholding method (VMD–WT) is proposed to improve the accuracy of tide level extraction. More accurate hydrological measurement data can be obtained by improving the extraction accuracy of the OTF GNSS tide level. Obtaining high-precision tidal data at the survey vessel and correcting the bathymetry data are prerequisites for obtaining high-quality seafloor topographic data when conducting marine topography survey.

This paper is structured as follows. In Section 2, the methodology of this paper is introduced, including the OTF GNSS tide measurement theory, OTF GNSS tide level extraction method, and the flow of the VMD–WT sea surface geodetic height filtering algorithm. An experimental strategy and experimental methods are shown in Section 3. In Section 4, the experimental procedure and results of the experiments using the VMD–WT method proposed in this paper are detailed, and the filtering effect of VMD–WT is compared with that of the other seven methods to verify the superiority of the VMD–WT method, and the experimental results are analyzed. Finally, the conclusions are drawn in Section 5.

2. Methodology

2.1. OTF GNSS Tide Measurement and Solution Method

The basic concept of our OTF GNSS tide solution is presented below. The high-precision geodetic height data of the GNSS receiver phase center (hereinafter, phase center) was obtained by using the GPS carrier phase differential technique. Then, the sea surface geodetic height was calculated through the height difference between the phase center and the sea surface. Afterward, the tide level based on the WGS84 reference ellipsoid in the sea surface geodetic height sequence (geodetic height tide level) was extracted by the filtering method. Subsequently, the tide level based on the depth datum was acquired through a vertical datum conversion (chart height tide level). The specific steps are described in the following subsections.

2.1.1. Instrument Placement and Coordinate Measurement

Using the GPS carrier phase differential technique requires setting up a reference station on a known point on the shore and strictly measuring the antenna height. The reference point of the inertial measurement unit (IMU) or the geometric center of the vessel can be selected as the reference origin of the vessel frame system (VFS). Regarding the ideal VFS, the X-axis points horizontally forward to the bow direction, the Y-axis points to starboard in the horizontal plane and is perpendicular to the X-axis, and the Z-axis is perpendicular to the XY plane and points downwards. The coordinates of the phase center and IMU in the ideal VFS should be strictly determined [7,9]. The definitions of the vessel frame system are presented in Figure 1.

2.1.2. Reduction in Sea Surface Geodetic Height

The instantaneous geodetic height of the phase center should be reduced to the sea surface through the coordinates of the phase center in the ideal VFS, the geodetic height data, attitude data, and pressure sensor data to accurately obtain the instantaneous geodetic height of the sea surface, as illustrated in Figure 2. Its specific steps are:

(1) When the ship is anchored and the hull attitude is stable, the distance $L_3$ from the phase center to the water surface is calculated by

$$L_3=L_1-L_2-L_4$$

(1)

where $L_1$ represents the vertical distance from the upper surface of the transducer to the phase center of the GNSS receiver; $L_2$ denotes the static draft measured by the pressure sensor; and $L_4$ indicates the distance from the center of the pressure sensor to the upper surface of the transducer.

(2) The survey ship is affected by factors such as wind, waves, hull manipulation, and dynamic draft when sailing. The heave motion produced by the survey ship causes changes in the vertical distance from the phase center to the sea surface. Under the influence of the lever arms from the phase center to the IMU reference point and the hull attitude, the heave measured by the IMU is not the phase center heave. The difference between the heave measured by the IMU and the heave at the center of the phase is reflected in the “induced heave” correction term. The heave calculation formula of the phase center is [22,23]

$$H_i=h_0+xsinP-ysinRcosP-z\left(cosRcosP-1\right)-\mathsf{\Delta }H$$

(2)

where $h_0$ represents the heave measured by the IMU; ($x,y,z$) denotes the coordinates of the phase center in the ideal VFS; $R$ and $P$ signify the roll and pitch values measured by the IMU, respectively; and $\mathsf{\Delta }H$ indicates the difference between the dynamic draft measured by the pressure sensor when the ship is sailing and the static draft measured when the ship is anchored.

(3) After the heave correction, the instantaneous vertical distance $H_m$ from the phase center to the sea surface is expressed as

$$H_m=L_3+H_i$$

(3)

(4) The instantaneous geodetic height of the sea surface is expressed as

$$h=h_{GPS}-H_m$$

(4)

where $h$ denotes the instantaneous geodetic height of the sea surface and $h_{GPS}$ refers to the geodetic height measured at the phase center.

(5) The sea surface instantaneous geodetic height under different epochs constitutes the sea surface geodetic height sequence.

2.1.3. Sea Surface Geodetic Height Sequence Filtering

The reduced sequence of the sea surface geodetic height, a nonperiodic nonstationary signal [24], is affected by factors such as waves, hull manipulation, and GNSS signal observation errors induced by radio transmission [25,26]. Thus, the sea surface geodetic height sequence needs to be filtered to extract the low-frequency geodetic height tide level.

2.1.4. Vertical Datum Conversion

Depth datum is the reference plane for the hydrographic survey. The elevation information directly measured by GNSS is based on the geodetic height of the reference ellipsoid, thus the geodetic height tide level needs to be converted to the chart height tide level [27]. Liu [28], Zhao et al. [8,29], Chang et al. [30], EI-Diasty et al. [31] lucubrated the vertical reference conversion, and the vertical reference conversion methods can be found in their papers.

2.2. OTF GNSS Tide Level Data—Extraction Method

Long-period tide level, short-period waves, GPS observation errors, some unremoved wave influence errors [32], and hull fluctuations caused by hull maneuvering constitute the sea surface geodetic height sequence. The period of change in the tide level is at least greater than 1 h, and the period of change for other elements is a few seconds to 10 min at most [8].

The relative distribution of tidal signals and nontidal signals in the frequency domain is obtained through an analysis of the components of the sea surface geodetic height sequence. A suitable filtering method is required to filter the sea surface geodetic height sequence for extracting the high-precision geodetic height tide level. The VMD–WT filtering method is introduced in the following subsections.

2.2.1. Wavelet Thresholding Method

The commonly used binary discrete wavelet transform formula is [33]

$$Wf\left(j,k\right)=2^{-\frac{j}{2}}{{\displaystyle \int }}_{-\infty }^{+\infty }f\left(t\right){\psi }^{\ast }\left(2^{-j}t-k\right)dt$$

(5)

The Mallat algorithm is a fast algorithm for the discrete wavelet transform of signals. According to the multiresolution analysis theory of the Mallat algorithm [34], the wavelet transform decomposition formula of the signal is

$$c_{j,k}={{\displaystyle \sum }}_{m\in Z}{h}_{m-2k}{c}_{j-1,m}$$

(6)

$$d_{j,k}={{\displaystyle \sum }}_{m\in Z}{g}_{m-2k}{c}_{j-1,m}$$

(7)

where $k=0, 1, 2,\cdots ,N-1$; $c_{j,k}$ denotes a smooth approximation sequence; $d_{j,k}$ represents the detail signal; $h,g$ are a pair of quadrature mirror filter banks; $j$ is the number of decomposition layers; $J=lo{g}_{2}N$ indicates the maximum number of decomposition layers; and $N$ signifies the number of discrete sampling points.

The multiresolution analysis of the wavelet transform can be regarded as passing the signal through the low-pass filter h and the high-pass filter $g$ to obtain the low-frequency part ${\mathrm{A}}_{\mathrm{i}}$ and the high-frequency part ${\mathrm{D}}_{\mathrm{i}}$ of the signal. In the next decomposition, the foregoing filtering process is repeated for the low-frequency part ${\mathrm{A}}_{\mathrm{i}}$ obtained by the previous decomposition. The decomposition model is presented in Figure 3.

The basic principle of the wavelet thresholding method is that the Mallat algorithm performs a j-layer decomposition for the sea surface geodetic height sequence to obtain wavelet coefficients at different scales. The wavelet coefficients are processed by selecting the appropriate threshold and threshold function. The wavelet coefficients are kept when they are greater than the threshold and the wavelet coefficients are set to zero when they are less than the threshold. The sea surface geodetic height sequence is denoised by reconstructing the zeroed wavelet coefficients where the noise is located and the wavelet coefficients of the low-frequency signal where the tidal signal is located. However, the wavelet transform forced noise elimination method is to set the wavelet coefficients corresponding to all high-frequency signals to zero, which tends to lose useful signals.

In this paper, we use the rigrsure threshold criterion and the hard threshold function for signal filtering.

2.2.2. Normalized Cross-Correlation Coefficient (NCC)

The NCC is often used to evaluate the similarity between two signals [35]. The value of the NCC is in the range of [–1,1]. A larger value of the NCC indicates that the two signals are more similar. The formula for the NCC is provided below.

$$NCC=\frac{{\sum }_{n=1}^N{S}_1\left(n\right)·S_2\left(n\right)}{\sqrt{\left({\sum }_{n=1}^N{S}_1^2\left(n\right)\right)·\left({\sum }_{n=0}^{N-1}{S}_2^2\left(n\right)\right)}}$$

(8)

where $S$₁ is the signal before filtering, $S$₂ is the signal after wavelet threshold filtering, and N represents the number of sampling points. In this paper, the NCC was used to describe the difference between waveforms before and after filtering by wavelet thresholding method to determine the optimal number of wavelet decomposition layers. The optimal number of decomposition layers was selected by setting the step size of decomposition layers to 1 and the range of [1,L] to calculate the NCC of the filtered signal and the pre-filtered signal, and the number of decomposition layers was a suitable value when the NCC value was stable. Normally, when the continuous time of marine topography survey is less than 8 h, and the signal-to-noise ratio of the sea surface geodesic height sequence is high, L can meet the need when L is taken as 50.

2.2.3. The Root-Mean-Square Error (RMSE)

In this paper, the RMSE was used to calculate the degree of deviation between the tide level extracted from the geodetic height sequence of the sea surface and the tide level of the tide gauge station. The smaller the RMSE, the closer the extracted geodetic height tide level is to the tide level of the tide gauge, and the better the filtering effect [36]. The formula for the RMSE is provided below.

$$RMSE=\sqrt{\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{\left[s_i\left(t\right)-s_i^{\prime }\left(t\right)\right]}^2}$$

(9)

where $s_i\left(t\right)$ denotes the tide level value measured by the tide gauge; $s_i^{\prime }\left(t\right)$ indicates the tide level value after filtering; and $N$ is the number of signal sampling points.

2.2.4. Variational Mode Decomposition

The variational mode decomposition (VMD) [19] algorithm is a multicomponent signal adaptive decomposition method. By iteratively searching for the optimal solution of the constrained variational model, it adaptively realizes the frequency domain segmentation of the signal and the efficient separation of the intrinsic mode functions (IMFs), which exhibits good noise robustness [20,37].

The VMD algorithm decomposes the original signal into a finite number of subsignals with an orderly arrangement of frequency sizes and limited bandwidth and center frequency, namely IMFs. Each IMF is defined as [38]

$$u_k\left(t\right)=A_k\left(t\right)cos\left({\varphi }_k\left(t\right)\right)$$

(10)

where $u_k\left(t\right)$ represents an IMF; $A_k\left(t\right)$ denotes the instantaneous amplitude of $u_k\left(t\right)$; ${\varphi }_k\left(t\right)$ indicates the phase; and $t$ is time.

The algorithm of the VMD adaptive decomposition is detailed as follows.

(1) Estimate the bandwidth of each IMF. The sum of the estimated bandwidths of the IMF is minimized by converting to solve the constrained variational problem. Moreover, the sum of each IMF is equal to the original signal $x\left(t\right)$. The constrained variational model expression isThe constrained variational model expression is

$$\begin{array}{c}\underset{\left\{u_k\right\},\left\{{\mathsf{\omega }}_k\right\}}{min}\left\{{\displaystyle \sum }_k\parallel {\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)\ast u_k\left(t\right)\right]e^{-j{\mathsf{\omega }}_{k}t}{\parallel }_2^2\right\}\\ s.t.{\displaystyle \sum }_k{u}_k=x\left(t\right)\end{array}$$

(11)

where $\left\{u_k\right\}=\left\{u_1,\cdots ,u_K\right\}$ represents each modal component;$\left\{{\mathsf{\omega }}_k\right\}=\left\{{\mathsf{\omega }}_1,\cdots ,{\mathsf{\omega }}_K\right\}$ indicates the center frequency of each modal component;$K$ denotes the number of modal components; and $x\left(t\right)$ refers to the original signal.

(2) A Lagrange multiplication operator $\lambda$ and penalty factor $\alpha$ are introduced to solve the optimal solution of (12). The augmented Lagrangian function of Equation (12) is

$$\mathrm{L}\left(\left\{{\mathrm{u}}_{\mathrm{k}}\right\},\left\{{\mathsf{\omega }}_{\mathrm{k}}\right\},\lambda \right)=\alpha {\displaystyle \sum }_{\mathrm{k}}\parallel {\partial }_{\mathrm{t}}\left[\left(\delta \left(\mathrm{t}\right)+\frac{\mathrm{j}}{\pi \mathrm{t}}\right)\ast {\mathrm{u}}_{\mathrm{k}}\left(\mathrm{t}\right)\right]{\mathrm{e}}^{-\mathrm{j}{\mathsf{\omega }}_{\mathrm{k}}\mathrm{t}}{\parallel }_2^2+\parallel \mathrm{f}\left(\mathrm{t}\right)-{\displaystyle \sum }_{\mathrm{k}}{\mathrm{u}}_{\mathrm{k}}\left(\mathrm{t}\right){\parallel }_2^2+\langle \lambda \left(\mathrm{t}\right),\mathrm{f}\left(\mathrm{t}\right)-{\displaystyle \sum }_{\mathrm{k}}{\mathrm{u}}_{\mathrm{k}}\left(\mathrm{t}\right)\rangle$$

(12)

(3) Equation (13) is solved using the alternating direction method of multipliers (ADMM) [39]. Specifically, the modal component ${ \mathrm{u}}_{\mathrm{k}}$, the center frequency ${\mathsf{\omega }}_{\mathrm{k}}$ corresponding to each modal component, and the Lagrangian multiplication operator $\mathsf{\lambda }$ are alternately updated in the frequency domain to solve the minimum point of $\mathrm{L}$. The updated formula is:

$${ \widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathsf{\omega }\right)=\frac{ \widehat{\mathrm{f}}\left(\mathsf{\omega }\right)-{{\displaystyle \sum }}_{\mathrm{i}<\mathrm{k}}{ \widehat{\mathrm{u}}}_{\mathrm{i}}^{\mathrm{n}+1}\left(\mathsf{\omega }\right)-{{\displaystyle \sum }}_{\mathrm{i}>\mathrm{k}}{\widehat{\mathrm{u}}}_{\mathrm{i}}^{\mathrm{n}}\left(\mathsf{\omega }\right)+\frac{{\widehat{\lambda }}^{\mathrm{n}}\left(\mathsf{\omega }\right)}{2}}{1+2\alpha {\left(\mathsf{\omega }-{\mathsf{\omega }}_{\mathrm{k}}^{\mathrm{n}}\right)}^2}$$

(13)

$${\mathsf{\omega }}_{\mathrm{k}}^{\mathrm{n}+1}=\frac{{{\displaystyle \int }}_0^{\infty }\mathsf{\omega }{\left|{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathsf{\omega }\right)\right|}^2\mathrm{d}\mathsf{\omega }}{{{\displaystyle \int }}_0^{\infty }{\left|{ \widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathsf{\omega }\right)\right|}^2\mathrm{d}\mathsf{\omega }}$$

(14)

$${\widehat{\lambda }}^{\mathrm{n}+1}\left(\mathsf{\omega }\right)={\widehat{\lambda }}^{\mathrm{n}}\left(\mathsf{\omega }\right)+\tau \left( \widehat{\mathrm{f}}\left(\mathsf{\omega }\right)-{{\displaystyle \sum }}_{\mathrm{k}}{ \widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathsf{\omega }\right)\right)$$

(15)

(4) The center frequency and bandwidth of each IMF component are continuously updated until the following termination conditions are met

$${{\displaystyle \sum }}_{\mathrm{k}}\parallel { \widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}-{ \widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}}{\parallel }_2^2/\parallel { \widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}}{\parallel }_2^2<\epsilon \left(\epsilon \mathrm{is} \mathrm{set} \mathrm{to} 1 \times {10}^{-7}\right)$$

(16)

The parameters of the VMD algorithm should be set in advance before the VMD algorithm is adopted to remove high-frequency noise from the signal. Research has suggested that two parameters have the greatest impact on the denoising effect of the signal: the penalty factor $\mathsf{\alpha }$ and the number of modal components $\mathrm{K}$ [36].

A smaller K results in insufficient decomposition of the original signal and then modal aliasing. Its prominent effect on this experiment is the presence of noise in the low-frequency modal components. However, false components are generated if K is too large. The smaller the α, the larger the bandwidth of each IMF obtained, and the more noise it contains. The larger the value of α, the smaller the bandwidth of the component signal, and the higher the decomposition accuracy. Nevertheless, a single component cannot contain all the information in its frequency band when the bandwidth is below a certain threshold, leading to a severe under-decomposition phenomenon [40,41].

2.2.5. Energy Difference Ratio Method

According to the integrity and orthogonality of IMF, Cheng et al. [15] proposed the energy difference tracking method. Briefly, whether the number K of modal components decomposed from the original signal is an appropriate value is determined through the difference $E_{err}$ between the energy sum $E_K$ of each modal component under different K values and the energy $E_X$ of the original signal. The smaller the value of $E_{err}$, the stronger the integrity and orthogonality of the decomposition results, and the more sufficient the decomposition. The calculation formula is

$$E_{IMFK}={{\displaystyle \sum }}_{i=1}^{n}IM{F}_K^2\left(t\right)$$

(17)

Where $E_{IMFK}$ represents the energy of each IMF; $n$ is the number of sampling points; and $IM{F}_K\left(t\right)$ indicates the Kth layer IMF.

$$E_K={{\displaystyle \sum }}_{k=1}^k{E}_{IMF{K}^{}}$$

(18)

where $E_K$ denotes the energy sum of IMFs after decomposition.

$$E_X={{\displaystyle \sum }}_{i=1}^n{x}^2\left(t\right)$$

(19)

where $E_X$ represents the energy of the original signal, $n$ is the number of sampling points, and $x\left(t\right)$ indicates the original signal.

$$E_{err}=|E_X-E_K|$$

(20)

where $E_{err}$ stands for the difference between the energy of the original signal and the energy sum of the decomposed IMFs.

As demonstrated by Bi et al. [42], and the experimental verification in this paper, the energy difference ratio method is suitable for determining the modal decomposition number K of the sea surface geodetic height sequence. During the first variational modal decomposition on the sea surface geodetic height sequence, with the increase in the K value, K becomes a suitable modal decomposition value when $E_{err}$/$E_X$ fluctuates around the smaller value. Similarly, during the second modal decomposition, as the value of K increases, K is a suitable modal decomposition value when $E_{err}$/$E_X$ fluctuates around the smaller value.

2.3. The VMD–WT Filtering Method

The tidal signal in the sea surface geodetic height sequence is a low-frequency signal, which is distributed in the low-frequency IMF. When the value of K is small, the signal decomposition is insufficient, and the low-frequency modal components contain a lot of noise. However, the larger the K value is, the longer the VMD algorithm takes to calculate the signal, especially for GNSS sampling data with a long time and a large quantity of data. To solve this problem, the IMF1 obtained by the first variational mode decomposition was decomposed again in this paper. In this way, only the center frequency and frequency bandwidth needed to be updated in the frequency domain where IMF1 was located, so as to achieve an efficient separation of tidal signal and noise.

Following the above analysis and theoretical basis, a sea surface geodetic height sequence filtering method based on VMD–WT is proposed in this paper. The algorithm steps are detailed as follows:

Step 1: The energy difference ratio method is utilized to determine the number K₁ of modal components for the first variational modal decomposition of the sea surface geodetic height sequence. As the value of K₁ increases, K₁ is a suitable modal decomposition value when $E_{err}$/$E_X$ fluctuates around a small value according to Equations (17)–(20). Then, the IMF1 obtained when the number of modal components is K₁ is taken out.

Step 2: The second modal decomposition is performed on the IMF1 obtained in Step1. The energy difference ratio method is still adopted to determine the number K₂ of modal components. K₂ is a suitable modal decomposition value when $E_{err2}$/$E_{x2}$ fluctuates around a small value according to Equations (17)–(20). Then, the IMF1 obtained when the number of modal components is K₂ is taken out.

Step 3: The decomposition level j of the WT is determined according to NCC. The number of decomposition layers corresponding to the stable NCC is selected. Then, filter a small amount of noise in the IMF1 obtained in step 2 by the WT. Select the rigrsure threshold criterion and a hard threshold function. Finally, the geodetic height tide level is extracted.

A flow chart of the VMD–WT filtering algorithm is presented in Figure 4.

3. Experimental Strategy and Experimental Methods

This section first presents an overview of the study area of the experiment and then describes the measurement and data processing process of the experiment

3.1. Study Area

A field experiment was conducted in the Yellow Sea waters of Qingdao, China on 28 August 2022 to verify the correctness of the method described in this paper. The experimental area and survey lines of the navigation experiment are presented in Figure 5a,b. The location of the tide gauge station was 35°52′52.6″N, 120°04′49.1″E. The latitude and longitude ranges of the experimental area were 35°51′27.3″–35°52′7.1″N and 120°04′42.4″–120°05′36.6″E, respectively.

3.2. The Tide Level of the Experimental Area

The tides near Qingdao are regular semidiurnal tides [43,44]. In particular, the reference ellipsoid was selected as the reference plane in the experiment to facilitate a comparative analysis of the filtering effects of the eight methods, without converting the geodetic height tide level to a chart height tide level. The reference ellipsoid can be regarded as a plane on a small scale. The M₂ tide is the largest tidal constituent which dominates the variations of tidal levels [45,46]. The shortest and longest distances between the survey lines and the tide gauge station were 1.7 km and 6.0 km, respectively.

The cotidal chart of the M₂ constituent in the Yellow Sea (Figure 6) was calculated by the EOT20 ocean tidal model, which was added in the nonstationary tidal analysis toolbox S_TIDE [17]. The tide gauge station and the experimental area were located near the 120 cm co-amplitude line, and the difference between the co-phase lines was within 5° [47,48]. In this experiment, the tide level value of the tide gauge after being filtered by the moving average method was taken as the tide level of the experimental area.

3.3. Measurement and Data Processing Flow

In this experiment, the process of OTF GNSS tide measurement and data processing was devised as follows. (1) The HI TARGET A8 Plus receiver was set up on the shore as a reference station, as illustrated in Figure 7a. The sampling frequency of the receiver was 1 Hz. The PPK (postprocessed kinematic) positioning adopted two Trimble AT1675-540TS receivers in the POSMV OCEANMASTER shipborne positioning and attitude system, and the Trimble receivers were used as rover stations, as illustrated in Figure 7b. The inertial measurement unit (IMU) of the POSMV OCEANMASTER system provided heave information, attitude information, and served as the reference origin of the VFS. An IMU was installed on the water. A pressure sensor was installed underwater. The pressure sensor collected dynamic draft data and static draft data. With a portable computer, POS MV software was used to collect attitude data and heave data measured by the IMU and 3D position data measured by the Trimble receivers.

A temporary tide gauge station was set up on the shore, and the DCX-25 pressure tide gauge was employed to measure the tide level of the experimental area synchronously, with a sampling interval of 1 min.

(2) The static data of the base station and the dynamic positioning data of the rover stations were subjected to a postdifferential processing of the carrier phase by Inertial Explorer 8.70 software, so as to obtain high-precision geodetic height data of the rover stations’ phase centers at different epochs. The data collected by the POSMV OCEANMASTER system were processed using POSPac 8.4 software to acquire the heave, attitude data, and offset value from the phase center to the reference point of the IMU. Additionally, the heave, attitude data, and geodetic height data of the rover stations obtained by PPK were unified by GPS time. The number of sampling points in this experiment was 27,835, and the sampling time was 7.73 h.

4. Results and Discussion

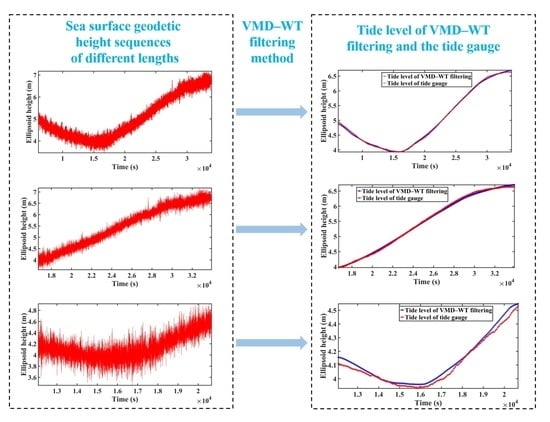
4.1. Filtering Method Combining Variational Mode Decomposition and Wavelet Transform (VMD–WT)

The statistical analysis suggested that the mean value of the standard deviation of the PPK positioning in this experiment in the vertical direction was 1.45 cm. The sea surface geodetic height sequence was obtained using Steps (1)–(5), detailed in Section 2.1.2 and illustrated in Figure 8a. A spectrogram of the sea surface geodetic height sequence is presented in Figure 8b. It can be seen in Figure 8b that the sea surface geodetic height sequence contains a lot of high-frequency noise. Figure 9 shows the standard deviation of each epoch in the vertical direction.

The process of extracting the geodetic height tide level from the sea surface geodetic height sequence by the VMD–WT filtering method proposed in this paper is detailed as follows.

The first modal decomposition number K₁ and the second modal decomposition number K₂ were determined according to the energy difference ratio method. As indicated in Figure 10a, ${\mathrm{E}}_{\mathrm{err}}/{\mathrm{E}}_{\mathrm{X}}$ fluctuated around 2.4 × 10⁻⁴ when K₁ = 40–80; thus, according to Step 1 of Section 2.3, K₁ = 60 was selected as the number of modal decomposition layers for the first decomposition in this experiment. As shown in Figure 10b, ${\mathrm{E}}_{\mathrm{err}2}/{\mathrm{E}}_{\mathrm{X}2}$ fluctuated around 2.4 × 10⁻⁵ when K₂ = 40–60; thus, according to Step 2 of Section 2.3, K₂ = 40 was selected as the number of modal decomposition layers for the second decomposition in this experiment.

When K₁ = 60 and K₂ = 40, five representative penalty factor values were selected from 1000–5000 to determine the penalty factor value suitable for the variational modal decomposition of the sea surface geodetic height sequence. Afterward, the RMSE between the IMF1 obtained by the second variational modal decomposition with different values of α and the tide level of tide gauge was investigated. As shown in Figure 11, the root-mean-square error reflected the closeness between the IMF1 and the tide gauge tide level after two variational modal decompositions. In this experiment, the α value of the first modal decomposition was set to be equal to the α value of the second modal decomposition.

It can be seen from Figure 11 that α is in the range of 1000–5000. The RMSE decreases as α increases, and the RMSE is smallest when α is 5000. It implies that the larger the value of α, the smaller the bandwidth of IMF1, and the more significant the separation effect between noise and signal. The low-frequency IMF1 is closer to the tide level of tide gauge.

Subsequently, the correctness of the parameters in two variational modal decompositions set to K₁ = 60, K₂ = 40, α1 = 5000, and α2 = 5000 was verified. Figure 12a shows the relative distribution of IMF1, IMF2, and IMF3 in the spectrogram obtained by the first modal decomposition when K₁ = 60 and α1 = 5000. There was no spectral aliasing phenomenon at the center frequencies of the three components, indicating that an appropriate K value was selected. The IMF1 obtained by the first modal decomposition contained both low-frequency tidal signals and high-frequency noise. From Figure 13a, it can be seen that the IMF1 obtained from the first variational modal decomposition contained high-frequency oscillations. Thus, the second variational modal decomposition was performed based on IMF1 to achieve an efficient signal-to-noise separation. Figure 12b shows the relative distribution of IMF1, IMF2, and IMF3 in the spectrogram obtained by the second modal decomposition when K₂ = 40 and α2 = 5000. It can be seen that the low-frequency tidal signal was well preserved in IMF1 (as proved by Zhao [8], the highest frequency of the tidal signal was 2.78 × 10⁻⁴ Hz, and the IMF2 component did not contain the low-frequency tidal signal), which suggested that a suitable α value was determined. Up to then, the tidal signal had been extracted into the IMF1 of the second modal decomposition. From Figure 13b, it can be seen that the signal after the second modal decomposition still had high-frequency oscillations. Finally, a small amount of noise contained in IMF1 was filtered out by the wavelet thresholding method.

With the purpose of removing all noise and keeping only low-frequency tidal signals, the following experiment determined the appropriate number of decomposition layers of the wavelet thresholding method by NCC. Figure 14a shows the NCC obtained when the wavelet thresholding method was performed on the signal after the second VMD decomposition with different number of decomposition layers. Figure 14b shows the RMSE between the filtered signal and the tide gauge tide level obtained at different decomposition layers.

As can be seen in Figure 14a, the NCC goes through four main phases, namely, the steady phase, the sharp-decline phase, the stable phase, and the decline phase. Figure 14b suggests that the RMSE similarly goes through four corresponding phases. It can be concluded that when the filtered signal is very similar to the prefiltered signal, i.e., the NCC is in the smooth stage, and the RMSE values between the filtered signal and the prefiltered signal are also in the smooth stage. When the NCC between the filtered signal and the prefiltered signal is in the decreasing stage, the RMSE value between the filtered signal and the prefiltered signal may be in the decreasing stage or in the increasing stage; in addition, the decreasing stage indicates that the wavelet thresholding filtering method has a noise cancellation effect, and the increasing stage demonstrates that the filtered signal starts to be distorted. There is a strong correlation between NCC and RMSE when filtering high signal-to-noise ratio sea surface geodesic high sequences, and a suitable number of decomposition layers of wavelet thresholding method can be selected by observing the change of NCC. Obviously, picking several points after the second smooth stage in Figure 14a can yield a good filtering effect. In this experiment, choosing the number of decomposition layers from 20 to 30 yielded a good filtering result.

Finally, the noise could be removed, and the tidal signal was preserved by zeroing the high-frequency coefficients and reconstructing with the low-frequency coefficients.

4.2. Comparative Analysis of the Eight Filtering Methods

The FFT low-pass filtering method, the EMD [49] filtering method, the EEMD [50] filtering method, the CEEMD [51] filtering method, the wavelet transform forced noise elimination method, the second-order polynomial fitting method, the third-order polynomial fitting method, and the VMD–WT methods were employed to extract the geodetic height tide level from the sea surface geodetic height sequence and we compared it with the tide level of the tide gauge. The filtering results of the eight methods were analyzed and evaluated. Figure 15 shows a comparison of the filtering effect between the geodetic height tide level extracted by the eight methods and the tide level of the tide gauge.

In the experiment, the sym4 wavelet, which has various advantages (e.g., continuity, compact support, approximate symmetry), was chosen as the wavelet basis function to perform the discrete wavelet transform. The number of comparison points in this experiment was 464, and the time interval between comparison points was 1 min.

As demonstrated in Figure 15f, the geodetic height tide level after FFT filtering is significantly different from the tide level of the tide gauge at both ends. FFT can only transform globally and cannot analyze locally, restricting its filtering effect on nonperiodic and nonstationary signals [52]. As demonstrated in Figure 15e, the difference between the tide level of geodetic height extracted by the wavelet transform forced noise elimination method and the tide level of the tide gauge reaches a maximum of 11.8 cm at the end of the data. The EMD method, EEMD method, and CEEMD method have the largest errors at the endpoints, with errors of 12.2 cm, 14.2 cm, and 14.1 cm, respectively, indicating that these three methods have a relatively serious endpoint effect, which increases the tidal level extraction error. As can be seen in Figure 15g, the error between the tide level value obtained from the second-order polynomial fit and the tide gauge tide level value is large. From Figure 15h, it can be seen that the error between the tide level of the third-order polynomial fit and the tide gauge tide level is still relatively pronounced, and the filtering result is not as good as that of the modal decomposition method, wavelet transform method, and VMD–WT method. Compared with the tide level of the tide gauge, the geodetic height tide level extracted by the VMD–WT method has the largest error in the initial part of the data, up to 7.2 cm, which is better than the other seven methods. On the whole, it is closer to the tide level of the tide gauge.

Subsequently, the filtering effects of the eight methods for 7.7 h were compared based on three indicators: maximum error value, RMSE, and error distribution.

The maximum error and RMSE of the eight filtering methods are listed in

Table 1. Comparison of filtering effects of the eight methods for 7.7 h.

Length of GNSS Tide Level	Method	FFT	Second-Order Polynomial Fit	Third-Order Polynomial Fit	EMD	EEMD	CEEMD	WT	VMD–WT
7.7 h	Maximum error (cm)	82.6	76.2	23.8	12.2	14.2	14.1	11.8	7.2
	RMSE (cm)	16.94	24.7	9.23	4.04	4.04	4.03	3.78	2.78

.

Table 1 shows that the maximum error value and RMSE of the proposed VMD-WT method are better than those of the other seven methods in the 7.7 h tide level experiment. The maximum error of the VMD–WT filtering method is lower than that of the FFT method, EMD method, EEMD method, CEEMD method, wavelet transform forced noise elimination method, second-order polynomial fitting method, and third-order polynomial fitting method by 75.4 cm, 5.0 cm, 7.0 cm, 6.9 cm, 4.6 cm, 69.0 cm, and 16.6 cm, respectively. The RMSE of the VMD–WT method is 14.16 cm, 1.26 cm, 1.26 cm, 1.25 cm, 1.0 cm, 21.9 cm and 6.5 cm lower than that of the other seven methods.

The error distribution between the geodetic height tide level extracted by the seven filtering methods and the tide level of the tide gauge was calculated. The advantages of the VMD–WT method were further illustrated by the proportion of different error intervals.

As can be observed in

Table 2. Extraction error distribution of the eight filtering methods for 7.7 h.

Length of GNSS Tide Level	Method	FFT	Second-Order Polynomial Fit	Third-Order Polynomial Fit	EMD	EEMD	CEEMD	WT	VMD–WT
7.7 h	0–5 cm	45.3%	10.1%	27.8%	81.7%	82.3%	79.5%	80.8%	94.2%
	5–10 cm	30.0%	10.1%	43.5%	16.6%	15.7%	18.3%	18.1%	5.8%
	10–15 cm	10.0%	13.0%	22.0%	1.7%	2.0%	2.2%	1.1%	0
	15–20 cm	5.7%	14.0%	5.6%	0	0	0	0	0
	0–90 cm	8.2%	52.8%	1.1%	0	0	0	0	0

, the extraction error of the FFT method for 7.7 h is distributed in 0–90 cm, the error ratio in 0–10 cm is 75.3%, the error ratio in 0–20 cm is 91.8%, and the maximum error is 82.6 cm. The first- and last-part values of the geodetic height tide level extracted after FFT filtering are extremely different from the tide level of the tide gauge. The tide level extraction error of the EMD method, EEMD method, and CEEMD method are all distributed in 0–15 cm, and the error in 0–10 cm accounts for 98.3%, 98%, and 97.8%, respectively. The tide level extraction error of the wavelet transform forced noise elimination method is distributed in 0–15 cm, and the error in 0–10 cm accounts for 98.9%. The tide level extraction error of the second-order polynomial fitting method is distributed in 0–80 cm, and the error in 0–10 cm accounts for 20.2%. The tide level extraction error of the third-order polynomial fitting method is distributed in 0–23.8 cm, and the error in 0–10 cm accounts for 71.3%. The tide level extraction error of the VMD–WT method is only distributed in 0–10 cm, and the error in 0–5 cm accounts for 94.2%.

To further demonstrate the robustness of our proposed VMD–WT method, we conducted two more experiments with different tide level lengths. One of the experiments had a tide level length of 4.8 h and the other one has a tide level length of 2.4 h. The 4.8 h and 2.4 h data are arbitrary intercepts from our 7.7 h of data.

As can be seen from Figure 16, the tide level at 4.8 h does not have clear tidal characteristics, but the proposed VMD–WT method still has the best agreement with the tide gauge tide level, especially from the tail. Compared to the 7.7 h tide level experiment, the filtering results of the CEEMD, EEMD and EMD methods are still better, but not as good as the proposed VMD–WT method. The filtering results of the FFT method, second-order polynomial fit are still not satisfactory, while the results of the third-order polynomial fit are better than those obtained in the 7.7 h tide level experiment.

Subsequently, the filtering effects of the eight methods for 4.8 h were compared based on three indicators: maximum error value, RMSE, and error distribution.

The maximum error and RMSE of the eight filtering methods are listed in

Table 3. Comparison of filtering effects of the eight methods for 4.8 h.

Length of GNSS Tide Level	Method	FFT	Second-Order Polynomial Fit	Third-Order Polynomial Fit	EMD	EEMD	CEEMD	WT	VMD–WT
4.8 h	Maximum error (cm)	141.0	26.5	8.6	12.3	14.3	14.3	13.0	7.2
	RMSE (cm)	25.72	10.0	4.17	4.47	4.54	4.59	4.45	3.13

.

Table 3 shows that the maximum error value and RMSE of the proposed VMD–WT method are better than those of the other seven methods in the 4.8 h tide level experiment. The maximum error of the VMD–WT filtering method is lower than that of the FFT method, EMD method, EEMD method, CEEMD method, wavelet transform forced noise elimination method, second-order polynomial fitting method, third-order polynomial fitting method by 133.8 cm, 5.1 cm, 7.1 cm, 7.1 cm, 5.8 cm, 19.3 cm, and 1.4 cm, respectively. The RMSE of the VMD–WT method is 22.59 cm, 1.34 cm, 1.41 cm, 1.46 cm, 1.32 cm, 6.87 cm, and 1.04 cm lower than that of the other seven methods.

The error distribution between the geodetic height tide level extracted by the seven filtering methods and the tide level of the tide gauge was calculated. The advantages of the VMD–WT method were further illustrated by the proportion of different error intervals.

As shown in

Table 4. Extraction error distribution of the eight filtering methods for 4.8 h.

Length of GNSS Tide Level	Method	FFT	Second-Order Polynomial Fit	Third-Order Polynomial Fit	EMD	EEMD	CEEMD	WT	VMD–WT
4.8 h	0–5 cm	45.2%	28.8%	71.2%	75.7%	72.9%	72.2%	73.6%	91.7%
	5–10 cm	22.9%	28.1%	28.8%	21.2%	24.3%	25.0%	22.9%	8.3%
	10–15 cm	9.4%	36.1%	0	3.1%	2.8%	2.8%	3.5%	0
	15–20 cm	6.9%	4.2%	0	0	0	0	0	0
	>20 cm	15.6%	2.8%	0	0	0	0	0	0

, in the 4.8 h experiment without significant tidal characteristics, the tide level extraction error of the VMD–WT method is only distributed in 0–10 cm, and the error in 0–5 cm accounts for 91.7%, which is better than the other seven methods. The second-order polynomial fitting method gives better filtering results than the other six methods. The FFT method and the second-order polynomial fitting method have the worst filtering results and the errors are more distributed in large error intervals. The error distribution results of EMD method, EEMD method, and CEEMD method are similar.

The following figure shows the comparison of the tide levels extracted by the eight methods in the 2.4 h tide level experiment with the tide gauge tide level.

As can be seen in Figure 17, the tide level extracted by the VMD–WT method are closer to the tide gauge tide level than that of the other methods, especially the tail. The method proposed in this paper also shows excellent filtering effect in short time tide level extraction.

Subsequently, the filtering effects of the eight methods for 2.4 h were compared based on three indicators: maximum error value, RMSE, and error distribution.

The maximum error and RMSE of the eight filtering methods are listed in

Table 5. Comparison of filtering effects of the eight methods for 2.4 h.

Length of GNSS Tide Level	Method	FFT	Second-Order Polynomial Fit	Third-Order Polynomial Fit	EMD	EEMD	CEEMD	WT	VMD–WT
2.4 h	Maximum error (cm)	24.5	12.7	11.5	8.9	8.6	9.9	9.6	6.0
	RMSE (cm)	6.3	4.32	4.32	3.97	4.06	4.03	3.91	2.82

.

Table 5 shows that the maximum error value and RMSE of the proposed VMD–WT method are better than those of the other seven methods in the 2.4 h tide level experiment. The maximum error of the VMD–WT filtering method is lower than that of the FFT method, EMD method, EEMD method, CEEMD method, wavelet transform forced noise elimination method, second-order polynomial fitting method, third-order polynomial fitting method by 18.5 cm, 2.9 cm, 2.6 cm, 3.9 cm, 3.6 cm, 6.7 cm, and 5.5 cm, respectively. The RMSE of the VMD-WT method is 3.48 cm, 1.15 cm, 1.24 cm, 1.21 cm, 1.09 cm, 1.5 cm and 1.50 cm lower than that of the other seven methods.

The error distribution between the geodetic height tide level extracted by the eight filtering methods and the tide level of the tide gauge was calculated. The advantages of the VMD–WT method were further illustrated by the proportion of different error intervals.

As shown in

Table 6. Extraction error distribution of the eight filtering methods for 2.4 h.

Length of GNSS Tide Level	Method	FFT	Second-Order Polynomial Fit	Third-Order Polynomial Fit	EMD	EEMD	CEEMD	WT	VMD–WT
	0–5 cm	75.0%	80.5%	79.9%	78.5%	75.7%	80.6%	77.1%	94.4%
	5–10 cm	12.5%	15.3%	17.3%	21.5%	24.3%	19.4%	22.9%	5.6%
2.4 h	10–15 cm	8.3%	4.2%	2.8%	0	0	0	0	0
	15–20 cm	2.1%	0	0	0	0	0	0	0
	>20 cm	2.1%	0	0	0	0	0	0	0

, the tide level extraction error of the VMD-WT method is only distributed in 0–10 cm in the 2.4 h experiment, and the error in 0–5 cm accounts for 94.4%, which is better than the other seven methods. The three tide level experiments of 7.7 h, 4.8 h, 2.4 h show that the extraction errors of the VMD–WT method are more concentrated in the small error interval, and its maximum error is smaller than that of the other seven methods. Thus, it is more suitable for water level correction of bathymetry.

FFT is a global signal processing method, which cannot analyze the local information of the signal, and is only suitable for processing stable signals. When there are abrupt values in the signal or the signal is nonperiodic, it will affect the whole spectrum of the signal, and the denoising effect of the signal will be seriously affected in the inverse Fourier transform, which is also the reason for the poor effect of the FFT filtering [36]. The EMD method, EEMD method, and CEEMD method are all recursive decomposition modes in nature, which have more serious endpoint effects and modal blending problems, and a lack of strict mathematical basis, so as to limit their decomposition effect.

The wavelet transform is a multiscale time–frequency analysis method, which can effectively realize the analysis of nonstationary signals. When using a wavelet transform for noise removal from a signal, only a fixed wavelet basis function can be selected. When the basis function of a wavelet is determined, only the same basis function can be used to analyze the whole signal. The result of the wavelet transform is the signal at a fixed scale, thus the adaptiveness of the wavelet transform is weak [40], which is also the reason why the filtering effect of the wavelet transform was inferior to that of the VMD-WT method.

The nonrecursive decomposition method of VMD effectively avoids the inherent defects of a recursive decomposition mode and effectively solves the problems of poor noise immunity, modal aliasing, and endpoint effect, and can better decompose each component of the original signal compared with the EMD, EEMD and CEEMD methods. The VMD–WT filtering method determined the appropriate number of modal components through the energy difference ratio method. The second modal decomposition was performed for the IMF1 obtained by the first modal decomposition of the sea surface geodetic height sequence to realize the efficient separation of tidal signals and noise. Subsequently, a relatively superior α value was determined by comparing the filtering effects of the sea surface geodetic height sequence with different penalty factor values of α. The VMD–WT filtering method adopted the combination of VMD and WT and achieved the efficient extraction of tidal signals with the adaptive decomposition characteristics of the VMD for signals, the solid mathematical theoretical foundation of the VMD, the advantages of suppressing high-frequency noise and the characteristics of the wavelet transform multiresolution analysis.

5. Conclusions

In this paper, the VMD–WT method was proposed to be applied to the high signal-to-noise ratio sea surface geodetic height sequence filtering, so as to extract the OTF GNSS tide level. The VMD–WT filtering method realized the “refined” filtering of the sea surface geodetic height sequence and further improved the extraction accuracy of the OTF GNSS tide level. The comparison experiments with eight filtering methods demonstrated that the VMD–WT method had more advantages in three indexes, the RMSE, maximum error, and error distribution, which could further improve the accuracy of marine topography survey.

(1) The maximum extraction errors of the VMD–WT method were 7.2 cm, 7.2 cm, and 6.0 cm in the 7.7 h, 4.8 h, and 2.4 h tide level experiments, respectively, which were lower than those of the other seven methods; the RMSE of the VMD–WT method were 2.78 cm, 3.13 cm, and 2.82 cm in the 7.7 h, 4.8 h, and 2.4 h tide level experiments, respectively, which were lower than those of the other seven methods. The extraction error of the VMD–WT method was more concentrated in the small error interval, and the error in 0–10 cm accounted for 100%.

(2) When the distance between the base station and the survey area was within 15 km, the PPK or RTK positioning method was able to solve the vertical solution with high accuracy (less than 3 cm). The VMD–WT method proposed in this paper could obtain a good tide level extraction by filtering the high signal-to-noise ratio sea surface geodetic height sequence.

The VMD–WT method proposed in this paper did not compare the filtering results of each α value in determining the value of the penalty factor. Instead, several representative α values only were selected for the comparative analysis to determine a relatively superior α value. In follow-up research, the accuracy of tide level extraction will be improved by determining the optimal α through other algorithms.

In this paper, the VMD–WT method was used to filter the sea surface geodetic height data with a high signal-to-noise ratio, and excellent tide level extraction results were obtained. However, the filtering effect of the method when the signal-to-noise ratio of the sea surface geodetic height sequence is low has not been further explored, and it will be a potential hotspot in the future.