Satellite-Derived Photosynthetically Available Radiation at the Coastal Arctic Seafloor
Abstract
:1. Introduction
2. Satellite and In Situ Data
2.1. Satellite Data
2.2. In Situ Data
Sensitivity of In Situ Sensors
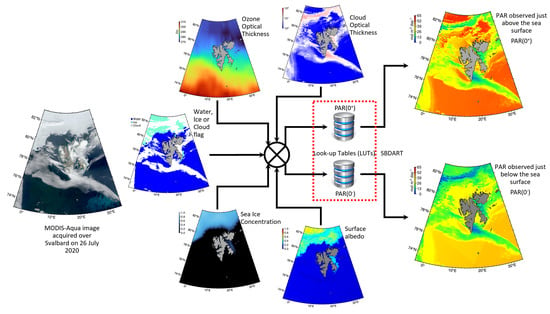
3. The PAR Algorithm
3.1. Water, Ice, or Cloud Flag ()
- Step 1:
- If , then there will not be enough light to calculate . Else, the pixel is assumed to contain water, = water.
- Step 2:
- The higher and lower represent clouds that are almost spectrally flat in the visible region. Therefore, when and , the pixel is assumed to contain cloud, = cloud.
- Step 3:
- The higher shows that is significantly higher than , which is more sensitive to temperature [62], pointing towards the presence of sea ice in the pixel. Furthermore, the effect of turbidity on can be minimized using . Hence, if and , the pixel is assumed to contain ice, = ice.
3.2. Mean Surface Albedo for PAR Bands ()
3.2.1. for Sea Ice under Clear Sky
3.2.2. for Water under Clear Sky
3.2.3. under Clouds
3.3. Cloud Optical Thickness ()
- (1)
- (665 nm band as reference wavelength) is sensitive to the cloud optical thickness and at , single scattering albedo of cloud is almost unity [77].
- (2)
- The absorption by clouds at is negligible [78].
- (3)
- The remains nearly spectrally constant in the visible range [79].
- (4)
- The transmittance of the atmosphere above the cloud is near unity.
- (5)
- The irradiance reflected by the surface, , is assumed to be transmitted to the bottom of the cloud ().
- (6)
- Multiple scattering between bright sea-ice surface and bottom of the cloud is ignored.
3.4. Calculation of PAR
3.4.1. PAR at Sea Surface
3.4.2. PAR Penetrating the Sea Surface in the Presence of Ice
3.4.3. PAR at Seafloor
3.5. Validation of Calculated PAR with In Situ Data
4. Results and Discussion
4.1. Accuracy of PAR() Derived from Satellite
4.2. Uncertainty in Satellite Estimation of PAR()
4.3. Comparison with Existing Algorithm
4.4. Trends of PAR() in the Coastal AO: A Brief Overview
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AO | Arctic Ocean |
| BOA | Bottom Of Atmosphere |
| CDOM | Coloured Dissolved Organic Matter |
| Chl-a | Chlorophyll-a concentration |
| DISORT | DIScrete-Ordinates Radiative Transfer |
| EO | Earth Observation |
| EP | Earth Probe |
| ISCCP | International Satellite Cloud Climatology Project |
| L1A | Level-1A |
| LBF2016 | Laliberté et al. [32] |
| LUTs | Look-Up Tables |
| M-K Test | Mann–Kendall Test |
| MODIS | MODerate-resolution Imaging Spectroradiometer |
| MPD | Median Percentage difference |
| NIR | Near-InfraRed |
| NSIDC | National Snow and Ice Data Center |
| OAC | Opticaly Active Constituent |
| OBDAAC | Ocean Biology Distributed Active Archive Center |
| OBPG | Ocean Biology Processing Group |
| OMI | Ozone Monitoring Instrument |
| PAR | Photosynthetically Available Radiation |
| PS | Present Study |
| SBDART | Santa Barbara DISORT Atmospheric Radiative Transfer |
| SIQR | Semi-InterQuartile range |
| SPM | Suspended Particulate Matter |
| SWIR | ShortWave-InfraRed |
| TOA | Top Of Atmosphere |
| TOMS | Total Ozone Mapping Spectrometer |
| UNIS | University Center in Svalbard |
| UQAR | Université du Québec à Rimouski |
References
- Maksym, T. Arctic and Antarctic Sea Ice Change: Contrasts, Commonalities, and Causes. Annu. Rev. Mar. Sci. 2019, 11, 187–213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Descamps, S.; Aars, J.; Fuglei, E.; Kovacs, K.M.; Lydersen, C.; Pavlova, O.; Pedersen, Å.Ø.; Ravolainen, V.; Strøm, H. Climate change impacts on wildlife in a High Arctic archipelago—Svalbard, Norway. Glob. Chang. Biol. 2017, 23, 490–502. [Google Scholar] [CrossRef]
- Cooley, S.W.; Ryan, J.C.; Smith, L.C.; Horvat, C.; Pearson, B.; Dale, B.; Lynch, A.H. Coldest Canadian Arctic communities face greatest reductions in shorefast sea ice. Nat. Clim. Chang. 2020, 10, 533–538. [Google Scholar] [CrossRef]
- Slagstad, D.; Wassmann, P.F.J.; Ellingsen, I. Physical constrains and productivity in the future Arctic Ocean. Front. Mar. Sci. 2015, 2, 85. [Google Scholar] [CrossRef] [Green Version]
- Tremblay, J.É.; Gagnon, J. The effects of irradiance and nutrient supply on the productivity of Arctic waters: A perspective on climate change. In Influence of Climate Change on the Changing Arctic and Sub-Arctic Conditions; Nihoul, J.C.J., Kostianoy, A.G., Eds.; Springer: Dordrecht, The Netherlands, 2009; Chapter 7; pp. 73–93. [Google Scholar] [CrossRef]
- Arrigo, K.R.; van Dijken, G.L. Continued increases in Arctic Ocean primary production. Prog. Oceanogr. 2015, 136, 60–70. [Google Scholar] [CrossRef]
- McCree, K.J. Photosynthetically Active Radiation. In Physiological Plant Ecology I; Lange, O.L., Nobel, P.S., Osmond, C.B., Ziegler, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; Chapter 2; pp. 41–55. [Google Scholar] [CrossRef]
- Gupta, M.; Follows, M.J.; Lauderdale, J.M. The Effect of Antarctic Sea Ice on Southern Ocean Carbon Outgassing: Capping Versus Light Attenuation. Glob. Biogeochem. Cycles 2020, 34, e2019GB006489. [Google Scholar] [CrossRef]
- Jönsson, B.F.; Sathyendranath, S.; Platt, T. Trends in Winter Light Environment Over the Arctic Ocean: A Perspective From Two Decades of Ocean Color Data. Geophys. Res. Lett. 2020, 47, e2020GL089037. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2011; p. 649. [Google Scholar]
- Lee, Z.; Weidemann, A.; Kindle, J.; Arnone, R.; Carder, K.L.; Davis, C. Euphotic zone depth: Its derivation and implication to ocean-color remote sensing. J. Geophys. Res. 2007, 112, C03009. [Google Scholar] [CrossRef]
- Nicolaus, M.; Katlein, C.; Maslanik, J.; Hendricks, S. Changes in Arctic sea ice result in increasing light transmittance and absorption. Geophys. Res. Lett. 2012, 39, 2012GL053738. [Google Scholar] [CrossRef] [Green Version]
- Wollschläger, J.; Neale, P.J.; North, R.L.; Striebel, M.; Zielinski, O. Editorial: Climate Change and Light in Aquatic Ecosystems: Variability & Ecological Consequences. Front. Mar. Sci. 2021, 8, 39–49. [Google Scholar] [CrossRef]
- Bélanger, S.; Babin, M.; Tremblay, J.É. Increasing cloudiness in Arctic damps the increase in phytoplankton primary production due to sea ice receding. Biogeosciences 2013, 10, 4087–4101. [Google Scholar] [CrossRef] [Green Version]
- Laney, S.R.; Krishfield, R.A.; Toole, J.M. The euphotic zone under Arctic Ocean sea ice: Vertical extents and seasonal trends. Limnol. Oceanogr. 2017, 62, 1910–1934. [Google Scholar] [CrossRef] [Green Version]
- Stroeve, J.; Vancoppenolle, M.; Veyssiere, G.; Lebrun, M.; Castellani, G.; Babin, M.; Karcher, M.; Landy, J.; Liston, G.E.; Wilkinson, J. A Multi-Sensor and Modeling Approach for Mapping Light Under Sea Ice During the Ice-Growth Season. Front. Mar. Sci. 2021, 7, 592337. [Google Scholar] [CrossRef]
- Connolly, C.T.; Cardenas, M.B.; Burkart, G.A.; Spencer, R.G.M.; McClelland, J.W. Groundwater as a major source of dissolved organic matter to Arctic coastal waters. Nat. Commun. 2020, 11, 1479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGovern, M.; Pavlov, A.K.; Deininger, A.; Granskog, M.A.; Leu, E.; Søreide, J.E.; Poste, A.E. Terrestrial Inputs Drive Seasonality in Organic Matter and Nutrient Biogeochemistry in a High Arctic Fjord System (Isfjorden, Svalbard). Front. Mar. Sci. 2020, 7, 542563. [Google Scholar] [CrossRef]
- Bonsell, C.; Dunton, K.H. Long-term patterns of benthic irradiance and kelp production in the central Beaufort sea reveal implications of warming for Arctic inner shelves. Prog. Oceanogr. 2018, 162, 160–170. [Google Scholar] [CrossRef]
- Krause-Jensen, D.; Duarte, C.M. Expansion of vegetated coastal ecosystems in the future Arctic. Front. Mar. Sci. 2014, 1, 77. [Google Scholar] [CrossRef] [Green Version]
- Filbee-Dexter, K.; Wernberg, T.; Fredriksen, S.; Norderhaug, K.M.; Pedersen, M.F. Arctic kelp forests: Diversity, resilience and future. Glob. Planet. Chang. 2019, 172, 1–14. [Google Scholar] [CrossRef]
- Krause-Jensen, D.; Archambault, P.; Assis, J.; Bartsch, I.; Bischof, K.; Filbee-Dexter, K.; Dunton, K.H.; Maximova, O.; Ragnarsdóttir, S.B.; Sejr, M.K.; et al. Imprint of Climate Change on Pan-Arctic Marine Vegetation. Front. Mar. Sci. 2020, 7, 1–27. [Google Scholar] [CrossRef]
- Marbà, N.; Krause-Jensen, D.; Masqué, P.; Duarte, C.M. Expanding Greenland seagrass meadows contribute new sediment carbon sinks. Sci. Rep. 2018, 8, 14024. [Google Scholar] [CrossRef] [Green Version]
- Goldsmit, J.; Schlegel, R.W.; Filbee-Dexter, K.; MacGregor, K.A.; Johnson, L.E.; Mundy, C.J.; Savoie, A.M.; McKindsey, C.W.; Howland, K.L.; Archambault, P. Kelp in the Eastern Canadian Arctic: Current and future predictions of habitat suitability and cover. Front. Mar. Sci. 2021, 18, 1453. [Google Scholar] [CrossRef]
- Laliberté, J.; Bélanger, S.; Babin, M. Seasonal and interannual variations in the propagation of photosynthetically available radiation through the Arctic atmosphere. Elem. Sci. Anthr. 2021, 9, 00083. [Google Scholar] [CrossRef]
- Matthes, L.C.; Mundy, C.J.; L.-Girard, S.; Babin, M.; Verin, G.; Ehn, J.K. Spatial Heterogeneity as a Key Variable Influencing Spring-Summer Progression in UVR and PAR Transmission Through Arctic Sea Ice. Front. Mar. Sci. 2020, 7, 183. [Google Scholar] [CrossRef]
- Frouin, R.; Ramon, D.; Boss, E.; Jolivet, D.; Compiègne, M.; Tan, J.; Bouman, H.; Jackson, T.; Franz, B.; Platt, T.; et al. Satellite Radiation Products for Ocean Biology and Biogeochemistry: Needs, State-of-the-Art, Gaps, Development Priorities, and Opportunities. Front. Mar. Sci. 2018, 5, 3. [Google Scholar] [CrossRef] [Green Version]
- IOCCG. IOCCG Report Number 16, Ocean Colour Remote Sensing in Polar Seas. In Reports and Monographs of the International Ocean Colour Coordinating Group; Babin, M., Arrigo, K.R., Bélanger, S., Forget, M.H., Eds.; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2015; Chapter 16; p. 130. [Google Scholar]
- Frouin, R.J.; Franz, B.A.; Werdell, P.J. The SeaWiFS PAR Product. In SeaWiFS Postlaunch Technical Report Series, Volume 22, Algorithm Updates for the Fourth SeaWiFS Data Reprocessing; Hooker, S.B., Firestone, E.R., Eds.; NASA Technical Memorandum: Greenbelt, MD, USA, 2003; Chapter 8; pp. 46–50. [Google Scholar]
- Frouin, R.; McPherson, J.; Ueyoshi, K.; Franz, B.A. A time series of photosynthetically available radiation at the ocean surface from SeaWiFS and MODIS data. In SPIE Asia-Pacific Remote Sensing, Proceedings of the Remote Sensing of the Marine Environment II, Kyoto, Japan, 29 October–1 November 2012; Frouin, R.J., Ebuchi, N., Pan, D., Saino, T., Eds.; SPIE: Kyoto, Japan, 2012; Volume 8525, p. 852519. [Google Scholar] [CrossRef]
- Somayajula, S.A.; Devred, E.; Bélanger, S.; Antoine, D.; Vellucci, V.; Babin, M. Evaluation of sea-surface photosynthetically available radiation algorithms under various sky conditions and solar elevations. Appl. Opt. 2018, 57, 3088. [Google Scholar] [CrossRef]
- Laliberté, J.; Bélanger, S.; Frouin, R.J. Evaluation of satellite-based algorithms to estimate photosynthetically available radiation (PAR) reaching the ocean surface at high northern latitudes. Remote Sens. Environ. 2016, 184, 199–211. [Google Scholar] [CrossRef]
- Frouin, R.; Tan, J.; Compiègne, M.; Ramon, D.; Sutton, M.; Murakami, H.; Antoine, D.; Send, U.; Sevadjian, J.; Vellucci, V. The NASA EPIC/DSCOVR Ocean PAR Product. Front. Remote Sens. 2022, 3, 1–17. [Google Scholar] [CrossRef]
- Gattuso, J.P.; Gentili, B.; Duarte, C.M.; Kleypas, J.A.; Middelburg, J.J.; Antoine, D. Light availability in the coastal ocean: Impact on the distribution of benthic photosynthetic organisms and their contribution to primary production. Biogeosciences 2006, 3, 489–513. [Google Scholar] [CrossRef] [Green Version]
- Morel, A. Optical modeling of the upper ocean in relation to its biogenous matter content (case I waters). J. Geophys. Res. 1988, 93, 10749. [Google Scholar] [CrossRef] [Green Version]
- Gattuso, J.P.; Gentili, B.; Antoine, D.; Doxaran, D. Global distribution of photosynthetically available radiation on the seafloor. Earth Syst. Sci. Data 2020, 12, 1697–1709. [Google Scholar] [CrossRef]
- Antoine, D.; Hooker, S.B.; Bélanger, S.; Matsuoka, A.; Babin, M. Apparent optical properties of the Canadian Beaufort Sea—Part 1: Observational overview and water column relationships. Biogeosciences 2013, 10, 4493–4509. [Google Scholar] [CrossRef] [Green Version]
- Masuda, K.; Takashima, T. The effect of solar zenith angle and surface wind speed on water surface reflectivity. Remote Sens. Environ. 1996, 57, 58–62. [Google Scholar] [CrossRef]
- Ricchiazzi, P.; Yang, S.; Gautier, C.; Sowle, D. SBDART: A Research and Teaching Software Tool for Plane-Parallel Radiative Transfer in the Earth’s Atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
- Rossow, W.B.; Schiffer, R.A. ISCCP Cloud Data Products. Bull. Am. Meteorol. Soc. 1991, 72, 2–20. [Google Scholar] [CrossRef]
- Saulquin, B.; Hamdi, A.; Gohin, F.; Populus, J.; Mangin, A.; D’Andon, O.F. Estimation of the diffuse attenuation coefficient KdPAR using MERIS and application to seabed habitat mapping. Remote Sens. Environ. 2013, 128, 224–233. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.; Hu, C.; Shang, S.; Du, K.; Lewis, M.; Arnone, R.; Brewin, R. Penetration of UV-visible solar radiation in the global oceans: Insights from ocean color remote sensing. J. Geophys. Res. Ocean. 2013, 118, 4241–4255. [Google Scholar] [CrossRef] [Green Version]
- Zheng, G.; Stramski, D.; Reynolds, R.A. Evaluation of the Quasi-Analytical Algorithm for estimating the inherent optical properties of seawater from ocean color: Comparison of Arctic and lower-latitude waters. Remote Sens. Environ. 2014, 155, 194–209. [Google Scholar] [CrossRef]
- Singh, R.K.; Shanmugam, P. A novel method for estimation of aerosol radiance and its extrapolation in the atmospheric correction of satellite data over optically complex oceanic waters. Remote Sens. Environ. 2014, 142, 188–206. [Google Scholar] [CrossRef]
- Babin, M.; Bélanger, S.; Ellingsen, I.; Forest, A.; Le Fouest, V.; Lacour, T.; Ardyna, M.; Slagstad, D. Estimation of primary production in the Arctic Ocean using ocean colour remote sensing and coupled physical-biological models: Strengths, limitations and how they compare. Prog. Oceanogr. 2015, 139, 197–220. [Google Scholar] [CrossRef]
- Lee, Y.J.; Matrai, P.A.; Friedrichs, M.A.M.; Saba, V.S.; Antoine, D.; Ardyna, M.; Asanuma, I.; Babin, M.; Bélanger, S.; Benoît-Gagné, M.; et al. An assessment of phytoplankton primary productivity in the Arctic Ocean from satellite ocean color/in situ chlorophyll-a based models. J. Geophys. Res. Ocean. 2015, 120, 6508–6541. [Google Scholar] [CrossRef]
- Singh, R.K.; Shanmugam, P.; He, X.; Schroeder, T. UV-NIR approach with non-zero water-leaving radiance approximation for atmospheric correction of satellite imagery in inland and coastal zones. Opt. Express 2019, 27, A1118. [Google Scholar] [CrossRef] [PubMed]
- Cavalieri, D.J.; Gloersen, P.; Campbell, W.J. Determination of sea ice parameters with the NIMBUS 7 SMMR. J. Geophys. Res. Atmos. 1984, 89, 5355–5369. [Google Scholar] [CrossRef]
- Meier, W.N.; Stewart, J.S.; Wilcox, H.; Hardman, M.A.; Scott, D.J. Near-Real-Time DMSP SSMIS Daily Polar Gridded Sea Ice Concentrations, Version 2; Technical Report; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021. [Google Scholar] [CrossRef]
- Maslanik, J.; Stroeve, J. Near-Real-Time DMSP SSMIS Daily Polar Gridded Sea Ice Concentrations, Version 1; Technical Report; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 1999. [Google Scholar] [CrossRef]
- TOMS Science Team. TOMS Earth-Probe Total Ozone (O3) Aerosol Index UV-Reflectivity UV-B Erythemal Irradiance Daily L3 Global 1 deg × 1.25 deg V008; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 1998.
- Bhartia, P.K. OMI/Aura TOMS-Like Ozone, Aerosol Index, Cloud Radiance Fraction L3 1 day 1 degree × 1 degree V3; Goddard Earth Sciences Data and Information Services Center: Greenbelt, MD, USA, 2012. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. In NOAA Technical Memorandum NESDIS NGDC-24; National Oceanic and Atmospheric Administration: Boulder, CO, USA, 2009; p. 25. [Google Scholar] [CrossRef]
- Dunton, K.; Bonsell, C.; Schonberg, S. Surface and Underwater Irradiance Timeseries from the Stefansson Sound, Beaufort Sea, Alaska, 1984–2018; University of Texas Marine Science Institute: Port Aransas, TX, USA, 2020. [Google Scholar] [CrossRef]
- IOCCG. IOCCG Report Number 18, Uncertainties in Ocean Colour Remote Sensing. In Reports and Monographs of the International Ocean-Colour Coordinating Group; Mélin, F., Ed.; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2019; Chapter 18; p. 164. [Google Scholar]
- Nunez, M.; Cantin, N.; Steinberg, C.; van Dongen-Vogels, V.; Bainbridge, S. Correcting PAR Data from Photovoltaic Quantum Sensors on Remote Weather Stations on the Great Barrier Reef. J. Atmos. Ocean. Technol. 2022, 39, 425–448. [Google Scholar] [CrossRef]
- Perovich, D.K.; Nghiem, S.V.; Markus, T.; Schweiger, A. Seasonal evolution and interannual variability of the local solar energy absorbed by the Arctic sea ice-ocean system. J. Geophys. Res. 2007, 112, C03005. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Garaba, S.P. Bright Oceans: Spectral Differentiation of Whitecaps, Sea Ice, Plastics, and Other Flotsam. In Recent Advances in the Study of Oceanic Whitecaps; Vlahos, P., Monahan, E.C., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2020; pp. 197–208. [Google Scholar] [CrossRef]
- Gerson, D.; Rosenfeld, A. Automatic sea ice detection in satellite pictures. Remote Sens. Environ. 1975, 4, 187–198. [Google Scholar] [CrossRef]
- Markus, T.; Cavalieri, D.J.; Ivanoff, A. The potential of using Landsat 7 ETM+ for the classification of sea-ice surface conditions during summer. Ann. Glaciol. 2002, 34, 415–419. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Shi, W. Detection of ice and mixed icewater pixels for MODIS ocean color data processing. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2510–2518. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. Atmos. 1998, 103, 32141–32157. [Google Scholar] [CrossRef]
- Warren, S.G. Optical properties of ice and snow. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2019, 377, 20180161. [Google Scholar] [CrossRef]
- Alekseeva, T.; Tikhonov, V.; Frolov, S.; Repina, I.; Raev, M.; Sokolova, J.; Sharkov, E.; Afanasieva, E.; Serovetnikov, S. Comparison of Arctic Sea Ice Concentrations from the NASA Team, ASI, and VASIA2 Algorithms with Summer and Winter Ship Data. Remote Sens. 2019, 11, 2481. [Google Scholar] [CrossRef] [Green Version]
- Kern, S.; Lavergne, T.; Notz, D.; Pedersen, L.T.; Tonboe, R.T.; Saldo, R.; Sørensen, A.M. Satellite passive microwave sea-ice concentration data set intercomparison: Closed ice and ship-based observations. Cryosphere 2019, 13, 3261–3307. [Google Scholar] [CrossRef]
- Coakley, J.A. Reflectance and albedo, Surface. Encycl. Atmos. Sci. 2003, 1914–1923. [Google Scholar] [CrossRef]
- Goyens, C.; Marty, S.; Leymarie, E.; Antoine, D.; Babin, M.; Bélanger, S. High Angular Resolution Measurements of the Anisotropy of Reflectance of Sea Ice and Snow. Earth Space Sci. 2018, 5, 30–47. [Google Scholar] [CrossRef] [Green Version]
- Gao, B.C.; Heidebrecht, K.B.; Goetz, A.F. Derivation of scaled surface reflectances from AVIRIS data. Remote Sens. Environ. 1993, 44, 165–178. [Google Scholar] [CrossRef]
- Wang, M. Atmospheric correction of ocean color sensors: Computing atmospheric diffuse transmittance. Appl. Opt. 1999, 38, 451. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443. [Google Scholar] [CrossRef]
- Franz, B.A.; Bailey, S.W.; Werdell, P.J.; McClain, C.R. Sensor-independent approach to the vicarious calibration of satellite ocean color radiometry. Appl. Opt. 2007, 46, 5068. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R. Physical Principles of Ocean Color Remote Sensing; University of Miami: Coral Gables, FL, USA, 2019. [Google Scholar] [CrossRef]
- Meister, G.; Kwiatkowska, E.J.; Franz, B.A.; Patt, F.S.; Feldman, G.C.; McClain, C.R. Moderate-Resolution Imaging Spectroradiometer ocean color polarization correction. Appl. Opt. 2005, 44, 5524. [Google Scholar] [CrossRef]
- Singh, R.K.; Shanmugam, P. A Multidisciplinary Remote Sensing Ocean Color Sensor: Analysis of User Needs and Recommendations for Future Developments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5223–5238. [Google Scholar] [CrossRef]
- NASA. Global Change Master Directory (GCMD)—Cloud Optical Depth/Thickness; NASA: Washington, DC, USA, 2022.
- King, M.D. Determination of the Scaled Optical Thickness of Clouds from Reflected Solar Radiation Measurements. J. Atmos. Sci. 1987, 44, 1734–1751. [Google Scholar] [CrossRef]
- Yang, P.; Baum, B.A. Satellite Remote Sensing|Cloud Properties. In Encyclopedia of Atmospheric Sciences; Holton, J.R., Curry, J.A., Pyle, J.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2003; pp. 1956–1965. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. A semianalytical cloud retrieval algorithm using backscattered radiation in 0.4–2.4 μm spectral region. J. Geophys. Res. 2003, 108, 4008. [Google Scholar] [CrossRef]
- Qiu, J. Cloud optical thickness retrievals from ground-based pyranometer measurements. J. Geophys. Res. 2006, 111, D22206. [Google Scholar] [CrossRef] [Green Version]
- Vermote, E. Introduction to Radiative Transfer Theory and Models (Optical Domain): Atmospheric Correction of Earth Observation Data for Environmental Monitoring Theory and Best Practices; Technical Report; NASA—Goddard Space Flight Center: Boulder, CO, USA, 2013.
- Pandey, P.; De Ridder, K.; Gillotay, D.; van Lipzig, N.P.M. Estimating cloud optical thickness and associated surface UV irradiance from SEVIRI by implementing a semi-analytical cloud retrieval algorithm. Atmos. Chem. Phys. 2012, 12, 7961–7975. [Google Scholar] [CrossRef] [Green Version]
- Laliberté, J. Light Available to Microalgae in the Arctic Ocean: A Satellite Perspective. Ph.D. Thesis, Département de Biologie, Université Laval, Québec, QC, Canada, 2020. [Google Scholar]
- Perovich, D.K. The Optical Properties of Sea Ice (CRREL Monograph); Technical Report; Cold Regions Research and Engineering Laboratory, Office of Naval Research: Hanover, NH, USA, 1996. [Google Scholar]
- Maykut, G.A.; Grenfell, T.C. The spectral distribution of light beneath first-year sea ice in the Arctic Ocean 1. Limnol. Oceanogr. 1975, 20, 554–563. [Google Scholar] [CrossRef]
- Campbell, K.; Mundy, C.J.; Barber, D.G.; Gosselin, M. Characterizing the sea ice algae chlorophyll a-snow depth relationship over Arctic spring melt using transmitted irradiance. J. Mar. Syst. 2015, 147, 76–84. [Google Scholar] [CrossRef]
- Krause-Jensen, D.; Sejr, M.K.; Bruhn, A.; Rasmussen, M.B.; Christensen, P.B.; Hansen, J.L.S.; Duarte, C.M.; Bruntse, G.; Wegeberg, S. Deep Penetration of Kelps Offshore Along the West Coast of Greenland. Front. Mar. Sci. 2019, 6, 1–7. [Google Scholar] [CrossRef]
- Borum, J.; Pedersen, M.F.; Krause-Jensen, D.; Christensen, P.B.; Nielsen, K. Biomass, photosynthesis and growth of Laminaria saccharina in a high-arctic fjord, NE Greenland. Mar. Biol. 2002, 141, 11–19. [Google Scholar] [CrossRef]
- Henley, W.J.; Dunton, K.H. Effects of nitrogen supply and continuous darkness on growth and photosynthesis of the arctic kelp Laminaria solidungula. Limnol. Oceanogr. 1997, 42, 209–216. [Google Scholar] [CrossRef]
- Lund-Hansen, L.C.; Markager, S.; Hancke, K.; Stratmann, T.; Rysgaard, S.; Ramløv, H.; Sorrell, B.K. Effects of sea-ice light attenuation and CDOM absorption in the water below the Eurasian sector of central Arctic Ocean (>88°N). Polar Res. 2015, 34, 23978. [Google Scholar] [CrossRef]
- Kauko, H.M.; Taskjelle, T.; Assmy, P.; Pavlov, A.K.; Mundy, C.J.; Duarte, P.; Fernández-Méndez, M.; Olsen, L.M.; Hudson, S.R.; Johnsen, G.; et al. Windows in Arctic sea ice: Light transmission and ice algae in a refrozen lead. J. Geophys. Res. Biogeosci. 2017, 122, 1486–1505. [Google Scholar] [CrossRef]
- Glukhovets, D.; Kopelevich, O.; Yushmanova, A.; Vazyulya, S.; Sheberstov, S.; Karalli, P.; Sahling, I. Evaluation of the CDOM Absorption Coefficient in the Arctic Seas Based on Sentinel-3 OLCI Data. Remote Sens. 2020, 12, 3210. [Google Scholar] [CrossRef]
- Seegers, B.N.; Stumpf, R.P.; Schaeffer, B.A.; Loftin, K.A.; Werdell, P.J. Performance metrics for the assessment of satellite data products: An ocean color case study. Opt. Express 2018, 26, 7404. [Google Scholar] [CrossRef] [Green Version]
- Bailey, S.W.; Werdell, P.J. A multi-sensor approach for the on-orbit validation of ocean color satellite data products. Remote Sens. Environ. 2006, 102, 12–23. [Google Scholar] [CrossRef]
- Kuhn, C.; de Matos Valerio, A.; Ward, N.; Loken, L.; Sawakuchi, H.O.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegl, R.; et al. Performance of Landsat-8 and Sentinel-2 surface reflectance products for river remote sensing retrievals of chlorophyll-a and turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef] [Green Version]
- Willmott, C.J.; Matsuura, K. On the use of dimensioned measures of error to evaluate the performance of spatial interpolators. Int. J. Geogr. Inf. Sci. 2006, 20, 89–102. [Google Scholar] [CrossRef]
- He, X.; Stamnes, K.; Bai, Y.; Li, W.; Wang, D. Effects of Earth curvature on atmospheric correction for ocean color remote sensing. Remote Sens. Environ. 2018, 209, 118–133. [Google Scholar] [CrossRef]
- Morel, A.; Huot, Y.; Gentili, B.; Werdell, P.J.; Hooker, S.B.; Franz, B.A. Examining the consistency of products derived from various ocean color sensors in open ocean (Case 1) waters in the perspective of a multi-sensor approach. Remote Sens. Environ. 2007, 111, 69–88. [Google Scholar] [CrossRef]
- Aumack, C.F.; Dunton, K.H.; Burd, A.B.; Funk, D.W.; Maffione, R.A. Linking light attenuation and suspended sediment loading to benthic productivity within an Arctic kelp-bed community. J. Phycol. 2007, 43, 853–863. [Google Scholar] [CrossRef]
- Gonçalves-Araujo, R.; Rabe, B.; Peeken, I.; Bracher, A. High colored dissolved organic matter (CDOM) absorption in surface waters of the central-eastern Arctic Ocean: Implications for biogeochemistry and ocean color algorithms. PLoS ONE 2018, 13, e0190838. [Google Scholar] [CrossRef] [Green Version]
- Kubryakov, A.; Stanichny, S.; Zatsepin, A. River plume dynamics in the Kara Sea from altimetry-based lagrangian model, satellite salinity and chlorophyll data. Remote Sens. Environ. 2016, 176, 177–187. [Google Scholar] [CrossRef]
- Osadchiev, A.A.; Pisareva, M.N.; Spivak, E.A.; Shchuka, S.A.; Semiletov, I.P. Freshwater transport between the Kara, Laptev, and East-Siberian seas. Sci. Rep. 2020, 10, 13041. [Google Scholar] [CrossRef]
- Gregg, W.W.; Carder, K.L. A simple spectral solar irradiance model for cloudless maritime atmospheres. Limnol. Oceanogr. 1990, 35, 1657–1675. [Google Scholar] [CrossRef]
- Letelier, R.M.; Karl, D.M.; Abbott, M.R.; Bidigare, R.R. Light driven seasonal patterns of chlorophyll and nitrate in the lower euphotic zone of the North Pacific Subtropical Gyre. Limnol. Oceanogr. 2004, 49, 508–519. [Google Scholar] [CrossRef] [Green Version]
- Boss, E.; Behrenfeld, M. In situ evaluation of the initiation of the North Atlantic phytoplankton bloom. Geophys. Res. Lett. 2010, 37, L18603. [Google Scholar] [CrossRef] [Green Version]
- Randelhoff, A.; Oziel, L.; Massicotte, P.; Bécu, G.; Galí, M.; Lacour, L.; Dumont, D.; Vladoiu, A.; Marec, C.; Bruyant, F.; et al. The evolution of light and vertical mixing across a phytoplankton ice-edge bloom. Elem. Sci. Anthr. 2019, 7, 20. [Google Scholar] [CrossRef] [Green Version]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 1994; p. 1012. [Google Scholar]
- Maritorena, S.; Morel, A.; Gentili, B. Diffuse reflectance of oceanic shallow waters: Influence of water depth and bottom albedo. Limnol. Oceanogr. 1994, 39, 1689–1703. [Google Scholar] [CrossRef]















| Region | Name | Latitude (°N) | Longitude (°E) | Measurement Depth (m) | Period | Source | |
|---|---|---|---|---|---|---|---|
| From | To | ||||||
| James Bay | C33-JB | 53.746 | −79.121 | 28 June 2019 | 23 August 2019 | UQAR | |
| V31-JB | 52.360 | −78.614 | 3 July 2019 | 20 August 2019 | |||
| Isfjorden | ISA | 78.223 | 15.652 | 19 February 2019 | 16 August 2020 | UNIS | |
| IAF | 78.233 | 15.689 | 1.2 | 17 June 2020 | 4 October 2020 | ||
| Stefansson Sound | Endeavor | 70.353 | −147.961 | 26 July 2002 | 9 August 2006 | [54] | |
| MPI | 70.353 | −147.961 | 26 July 2007 | 13 July 2018 | |||
| DS11 | 70.322 | −147.578 | 6.1 | 25 July 2004 | 14 July 2018 | ||
| E1 | 70.314 | −147.732 | 4.4 | 25 July 2004 | 14 July 2018 | ||
| E2 | 70.318 | −147.715 | 4.3 | 22 July 2005 | 3 August 2006 | ||
| L1 | 70.289 | −147.613 | 5.5 | 31 August 2014 | 14 July 2018 | ||
| W1 | 70.370 | −147.873 | 6.0 | 27 August 2014 | 8 September 2014 | ||
| W2 | 70.370 | −147.859 | 6.2 | 22 July 2005 | 9 August 2006 | ||
| W3 | 70.376 | −147.794 | 6.6 | 30 July 2016 | 16 September 2017 | ||
| Position (Depth) | Station/Mooring | mR (±SIQR) | MPD (%) | Bias | r | N | |
|---|---|---|---|---|---|---|---|
| Sea surface ( m) | C33-JB | 1.03 (±0.18) | 19.29 | 0.87 | 0.83 | 0.76 | 132 |
| V31-JB | |||||||
| Endeavor | |||||||
| MPI | 1.14 (±0.21) | 24.47 | 3.81 | 1.10 | 0.94 | 1190 | |
| ISA | 0.63 (±0.16) | 37.36 | −9.47 | 1.10 | 0.90 | 378 | |
| Seafloor (6.1 m) | DS11 | 1.48 (±1.03) | 76.71 | 0.54 | 0.71 | 0.74 | 381 |
| Seafloor (4.4 m) | E1 | ||||||
| Seafloor (4.3 m) | E2 | ||||||
| Seafloor (5.5 m) | L1 | ||||||
| Seafloor (6.0 m) | W1 | ||||||
| Seafloor (6.2 m) | W2 | ||||||
| Seafloor (6.6 m) | W3 | ||||||
| Subsurface (1.2 m) | IAF |
| Measurement Depth (m) | Station/Mooring | mR (±SIQR) | MPD (%) | Bias | r | |||
|---|---|---|---|---|---|---|---|---|
| MPI | 1.15 (±0.20) | 24.27 | 3.58 | 1.08 | 0.94 | 373 | 892 | |
| ISA | 0.60 (±0.17) | 40.31 | −7.92 | 1.04 | 0.92 | 72 | 115 | |
| 6.1 | DS11 | 0.79 (±1.03) | 61.07 | 0.12 | 0.61 | 0.48 | 11 | 18 |
| 4.4 | E1 | |||||||
| 4.3 | E2 | |||||||
| 6.2 | W2 | |||||||
| 1.2 | IAF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, R.K.; Vader, A.; Mundy, C.J.; Søreide, J.E.; Iken, K.; Dunton, K.H.; Castro de la Guardia, L.; Sejr, M.K.; Bélanger, S. Satellite-Derived Photosynthetically Available Radiation at the Coastal Arctic Seafloor. Remote Sens. 2022, 14, 5180. https://doi.org/10.3390/rs14205180
Singh RK, Vader A, Mundy CJ, Søreide JE, Iken K, Dunton KH, Castro de la Guardia L, Sejr MK, Bélanger S. Satellite-Derived Photosynthetically Available Radiation at the Coastal Arctic Seafloor. Remote Sensing. 2022; 14(20):5180. https://doi.org/10.3390/rs14205180
Chicago/Turabian StyleSingh, Rakesh Kumar, Anna Vader, Christopher J. Mundy, Janne E. Søreide, Katrin Iken, Kenneth H. Dunton, Laura Castro de la Guardia, Mikael K. Sejr, and Simon Bélanger. 2022. "Satellite-Derived Photosynthetically Available Radiation at the Coastal Arctic Seafloor" Remote Sensing 14, no. 20: 5180. https://doi.org/10.3390/rs14205180
APA StyleSingh, R. K., Vader, A., Mundy, C. J., Søreide, J. E., Iken, K., Dunton, K. H., Castro de la Guardia, L., Sejr, M. K., & Bélanger, S. (2022). Satellite-Derived Photosynthetically Available Radiation at the Coastal Arctic Seafloor. Remote Sensing, 14(20), 5180. https://doi.org/10.3390/rs14205180