An Envelope Travel-Time Objective Function for Reducing Source–Velocity Trade-Offs in Wave-Equation Tomography
Abstract
:1. Introduction
2. Methods
Envelope Travel-Time Wave-Equation Tomography
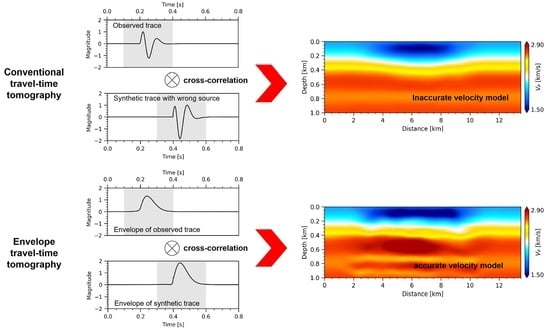
3. Numerical Results
3.1. Synthetic Inversion Example with Cross-Well Survey
3.2. Field Data Application
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Conventional Wave-Equation Travel-Time Tomography
References
- Tarantola, A. Inversion of seismic reflection data in the acoustic approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Woodward, M. Wave-equation tomography. Geophysics 1992, 57, 231–248. [Google Scholar] [CrossRef]
- Pratt, R.G.; Shin, C.; Hicks, G.J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophys. J. Int. 1998, 133, 341–362. [Google Scholar] [CrossRef]
- Tromp, J.; Tape, C.; Liu, Q. Seismic tomography, adjoint methods, time reversal, and banana-doughnut kernels. Geophysics 2005, 160, 195–216. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Jin, S.; Wu, R. Wave-equation-based seismic illumination analysis. Geophysics 2006, 71, S169–S177. [Google Scholar] [CrossRef]
- Tape, C.; Liu, Q.; Maggi, A.; Tromp, J. Adjoint tomography of the southern California crust. Science 2009, 325, 988–992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, R.; Wang, B.; Hu, C. Renormalized nonlinear sensitivity kernel and inverse thin-slab propagator in T-matrix formalism for wave-equation tomography. Inverse Probl. 2015, 31, 115004. [Google Scholar] [CrossRef] [Green Version]
- Bozdağ, E.; Peter, D.; Lefebvre, M.; Komatitsch, D.; Tromp, J.; Hill, J.; Podhorszki, N.; Pugmire, D. Global adjoint tomography: First-generation model. Geophys. J. Int. 2016, 207, 1739–1766. [Google Scholar] [CrossRef] [Green Version]
- Operto, S.; Miniussi, A. On the role of density and attenuation in 3D multi-parameter visco-acoustic VTI frequency-domain FWI: An OBC case study from the North Sea. Geophys. J. Int. 2018, 213, 2037–2059. [Google Scholar] [CrossRef] [Green Version]
- Bunks, C.; Saleck, F.M.; Zaleski, S.; Chavent, G. Multiscale seismic waveform inversion. Geophysics 1995, 60, 1457–1473. [Google Scholar] [CrossRef]
- Wu, R.; Luo, J.; Wu, B. Seismic envelope inversion and modulation signal model. Geophysics 2014, 79, WA13–WA24. [Google Scholar] [CrossRef]
- Yuan, Y.O.; Simons, F.J.; Bozdaǧ, E. Multiscale adjoint waveform tomography for surface and body waves. Geophysics 2015, 80, R281–R302. [Google Scholar] [CrossRef] [Green Version]
- Luo, J.; Wu, R. Seismic envelope inversion: Reduction of local minima and noise resistance. Geophys. Prospect. 2015, 63, 597–614. [Google Scholar] [CrossRef]
- Métivier, L.; Brossier, R.; Mérigot, Q.; Oudet, E.; Virieux, J. Measuring the misfit between seismograms using an optimal transport distance: Application to full waveform inversion. Geophys. J. Int. 2016, 205, 345–377. [Google Scholar] [CrossRef]
- Yao, G.; Wu, D.; Wang, S. A review of reflection-waveform inversion. Pet. Sci. 2020, 17, 334–351. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Schuster, G.T. Wave-equation traveltime inversion. Geophysics 1991, 56, 645–653. [Google Scholar] [CrossRef]
- Zhou, C.; Schuster, G.T.; Hassanzadeh, S.; Harris, J.M. Elastic wave equation traveltime and waveform inversion of crosswell data. Geophysics 1997, 62, 853–868. [Google Scholar] [CrossRef]
- Leeuwen, T.; Mulder, W.A. A correlation-based misfit criterion for wave-equation traveltime tomography. Geophys. J. Int. 2010, 182, 1383–1394. [Google Scholar] [CrossRef] [Green Version]
- Chi, B.; Dong, L.; Liu, Y. Correlation-based reflection full-waveform inversion. Geophysics 2015, 80, R189–R202. [Google Scholar] [CrossRef]
- Luo, Y.; Ma, Y.; Wu, Y.; Liu, H.; Gao, L. Full-traveltime inversion. Geophysics 2016, 81, R261–R274. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, Y.; Luo, Q.; Chang, X.; Zeng, R.; Wang, B.; Zhao, X. Frequency-dependent reflection wave-equation traveltime inversion from walkaway vertical seismic profile data. Geophysics 2019, 84, R947–R961. [Google Scholar] [CrossRef]
- Feng, B.; Xu, W.; Wu, R.; Xie, X.; Wang, H. Finite-frequency traveltime tomography using the Generalized Rytov approximation. Geophys. J. Int. 2020, 221, 1412–1426. [Google Scholar] [CrossRef]
- Zhang, H.; Thurber, C.H. Double-difference tomography: The method and its application to the Hayward Fault, California. Bull. Seismol. Soc. Am. 2003, 3, 1875–1889. [Google Scholar] [CrossRef]
- Fichtner, A. Full Seismic Waveform Inversion for Structural and Source Parameters. Ph.D. Thesis, Ludwig Maximilian University, Munich, Germany, 2010. [Google Scholar]
- Fichtner, A. Source-structure trade-offs in ambient noise correlations. Geophys. J. Int. 2015, 202, 678–694. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.O.; Simons, F.J.; Tromp, J. Double-difference adjoint seismic tomography. Geophys. J. Int. 2016, 206, 1599–1618. [Google Scholar] [CrossRef] [Green Version]
- Sager, K.; Ermert, L.; Boehm, C.; Fichtner, A. Towards full waveform ambient noise inversion. Geophys. J. Int. 2018, 212, 566–590. [Google Scholar] [CrossRef]
- Blom, N.; Hardalupas, P.S.; Rawlinson, N. Mitigating the effect of errors in source parameters on seismic (waveform) tomography. Geophys. J. Int. 2022, 232, 810–828. [Google Scholar] [CrossRef]
- Operto, S.; Gholami, Y.; Prieux, V.; Ribodetti, A.; Brossier, R.; Métivier, L.; Virieux, J. A guided tour of multiparameter full waveform inversion with multicomponent data: From theory to practice. Lead. Edge 2013, 32, 1040–1054. [Google Scholar] [CrossRef]
- Pan, W.; Innanen, K.A.; Margrave, G.F.; Fehler, M.C.; Fang, X.; Li, J. Estimation of elastic constants for HTI media using Gauss-Newton and full-Newton multiparameter full-waveform inversion. Geophysics 2016, 81, R275–R291. [Google Scholar] [CrossRef]
- Pan, W.; Geng, Y.; Innanen, K.A. Interparameter trade-off quantification and reduction in isotropic-elastic full-waveform inversion: Synthetic experiments and Hussar data set application. Geophys. J. Int. 2018, 213, 1305–1333. [Google Scholar] [CrossRef]
- Métivier, L.; Bretaudeau, F.; Brossier, R.; Virieux, J.; Operto, S. Full waveform inversion and the truncated Newton method: Quantitative imaging of complex subsurface structures. Geophys. Prospect. 2014, 62, 1353–1375. [Google Scholar] [CrossRef] [Green Version]
- Pan, W.; Innanen, K.A.; Liao, W. Accelerating Hessian-free Gauss-Newton full-waveform inversion via l-BFGS preconditioned conjugate-gradient algorithm. Geophysics 2017, 32, R49–R64. [Google Scholar] [CrossRef]
- Epanomeritakis, I.; Akçelik, V.; Ghattas, O.; Bielak, J. A Newton-CG method for large-scale three-dimensional elastic full-waveform seismic inversion. Inverse Probl. 2008, 24, 034015. [Google Scholar] [CrossRef]
- Taner, M.T.; Koehler, F.; Sheriff, R.E. Complex seismic trace analysis. Geophysics 1979, 44, 1041–1063. [Google Scholar] [CrossRef]
- Chen, G.; Wu, R.; Wang, Y.; Chen, S. Multi-scale signed envelope inversion. J. Appl. Geophys. 2018, 153, 113–126. [Google Scholar] [CrossRef]
- Gao, Z.; Pan, Z.; Gao, J.; Wu, R. Frequency controllable envelope operator and its application in multiscale full-waveform inversion. IEEE Trans. Geosci. Remote Sens. 2019, 57, 683–699. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, R.; Huang, X.; Long, Y.; Xu, Y.; Han, L. Phase-amplitude-based polarized direct envelope inversion in the time-frequency domain. Geophysics 2022, 87, R245–R260. [Google Scholar] [CrossRef]
- Pan, W.; Innanen, K.A. Amplitude-based misfit functions in viscoelastic full-waveform inversion applied to walk-away vertical seismic profile data. Geophysics 2019, 84, B335–B351. [Google Scholar] [CrossRef]
- Bozdağ, E.; Trampert, J.; Tromp, J. Misfit functions for full waveform inversion based on instantaneous phase and envelope measurements. Geophys. J. Int. 2011, 185, 845–870. [Google Scholar] [CrossRef]
- Pan, W.; Innanen, K.A.; Wang, Y. SeisElastic2D: An open-source package for multiparameter full-waveform inversion in isotropic-, anisotropic- and visco-elastic media. Comput. Geosci. 2020, 145, 104586. [Google Scholar] [CrossRef]
- Kim, H.J.; Lee, K.H. Source-independent full-waveform inversion of seismic data. Geophysics 2003, 68, 2010–2015. [Google Scholar]
- Xu, K.; Greenhalgh, S.A.; Wang, M. Comparison of source-independent methods of elastic waveform inversion. Geophysics 2006, 71, R91–R100. [Google Scholar] [CrossRef]
- Alkhalifah, T.; Choi, Y. Source-independent time-domain waveform inversion using convolved wavefields: Application to the encoded multisource waveform inversion. Geophysics 2011, 76, R125–R134. [Google Scholar]
- Zhang, Q.; Zhou, H.; Li, Q.; Chen, H.; Wang, J. Robust source-independent elastic full-waveform inversion in the time domain. Geophysics 2016, 81, R29–R44. [Google Scholar] [CrossRef]
- Liu, Q.; Tromp, J. Finite-frequency kernels based on adjoint methods. Bull. Seismol. Soc. Am. 2006, 96, 2383–2397. [Google Scholar] [CrossRef] [Green Version]
- Byrd, R.H.; Lu, P.; Nocedal, J. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Nocedal, J. Updating quasi-Newton matrices with limited storage. Math. Comput. 1980, 35, 773–782. [Google Scholar] [CrossRef]
- Nocedal, L.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: Cham, Switzerland, 2006; pp. 30–63. [Google Scholar]


















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, W.; Ma, N.; Wang, Y. An Envelope Travel-Time Objective Function for Reducing Source–Velocity Trade-Offs in Wave-Equation Tomography. Remote Sens. 2022, 14, 5223. https://doi.org/10.3390/rs14205223
Pan W, Ma N, Wang Y. An Envelope Travel-Time Objective Function for Reducing Source–Velocity Trade-Offs in Wave-Equation Tomography. Remote Sensing. 2022; 14(20):5223. https://doi.org/10.3390/rs14205223
Chicago/Turabian StylePan, Wenyong, Ning Ma, and Yanfei Wang. 2022. "An Envelope Travel-Time Objective Function for Reducing Source–Velocity Trade-Offs in Wave-Equation Tomography" Remote Sensing 14, no. 20: 5223. https://doi.org/10.3390/rs14205223
APA StylePan, W., Ma, N., & Wang, Y. (2022). An Envelope Travel-Time Objective Function for Reducing Source–Velocity Trade-Offs in Wave-Equation Tomography. Remote Sensing, 14(20), 5223. https://doi.org/10.3390/rs14205223