LiDAR Odometry and Mapping Based on Neighborhood Information Constraints for Rugged Terrain
Abstract
:1. Introduction
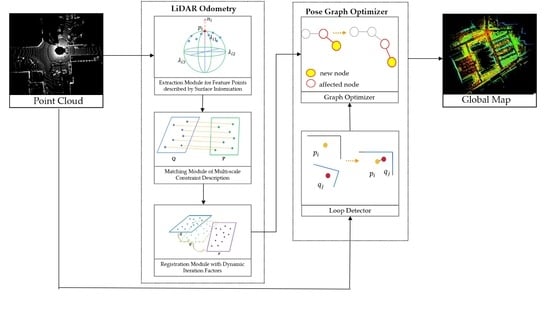
- A feature point extraction method based on surface information description is proposed, which effectively promotes the describing ability of point cloud features’ description of rugged scenes by extracting the features with high discriminability and value based on the differences in the point cloud neighborhood surface.
- A multi-scale constraint description method is proposed, which lessens the possibility of mis-registration and matching failure by integrating the surface information of the feature points, such as curvature and normal vector angle, as well as the distance information between the feature points to enhance the discrimination of the differences between the point cloud data of adjacent frames in rugged terrains.
- Dynamic iteration factors are introduced to the point cloud registration method, which reduce the dependence of the registration process on the initial pose by adjusting the thresholds of distance and angle in the iteration to modify the corresponding relationship of matching point pairs.
- A comprehensive evaluation of our solution is made over the KITTI sequences with a 64-beam LiDAR and the campus datasets of Jilin University collected by a 32-beam LiDAR, and the results demonstrate the validity of our proposed LCD method.
2. Related Work
2.1. Traditional LiDAR-Based SLAM Method
2.2. LiDAR-Based SLAM Method for Rugged Scenes
2.3. LiDAR-Based SLAM Method for Rugged Scenes
3. Materials and Methods
3.1. Algorithm Overview
3.2. Extraction Module for Feature Points Described by Surface Information
3.2.1. Surface Feature Construction
3.2.2. Adaptive Extraction of Feature Points
3.3. Matching Module of Multi-Scale Constraint Description
3.4. Registration Module with Dynamic Iteration Factors
4. Experiments
4.1. Datasets
4.1.1. KITTI Dataset
4.1.2. JLU Campus Dataset
4.2. Experimental Results and Analysis
4.2.1. KITTI Dataset
- Ablation Experiment
- 2.
- Comparative Experiment
4.2.2. Experiments on the JLU Dataset
- Ablation Experiment
- 2.
- Comparative Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thrun, S. Probabilistic robotics. Commun. ACM 2002, 45, 52–57. [Google Scholar] [CrossRef]
- Li, S.; Li, L.; Lee, G.; Zhang, H. A Hybrid Search Algorithm for Swarm Robots Searching in an Unknown Environment. PLoS ONE 2014, 9, e111970. [Google Scholar] [CrossRef] [PubMed]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 30 April 1992; pp. 586–606. [Google Scholar]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-icp. In Proceedings of the 2009 Robotics: Science and Systems, University of Washington, Seattle, WA, USA, 28 June 28–1 July 2009; p. 435. [Google Scholar]
- Du, S.; Liu, J.; Zhang, C.; Zhu, J.; Li, K. Probability iterative closest point algorithm for m-D point set registration with noise. Neurocomputing 2015, 157, 187–198. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the 2014 Robotics: Science and Systems, Berkeley, CA, USA, 13–15 July 2015; pp. 1–9. [Google Scholar]
- Shan, T.; Englot, B. Lego-loam: Lightweight and ground-optimized lidar odometry and mapping on variable terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE international conference on robotics and automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar]
- Park, C.; Moghadam, P.; Kim, S.; Elfes, A.; Fookes, C.; Sridharan, S. Elastic lidar fusion: Dense map-centric continuous-time slam. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1206–1213. [Google Scholar]
- Koide, K.; Miura, J.; Menegatti, E. A portable three-dimensional LIDAR-based system for long-term and wide-area people behavior measurement. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419841532. [Google Scholar] [CrossRef]
- Behley, J.; Stachniss, C. Efficient Surfel-Based SLAM using 3D Laser Range Data in Urban Environments. In Proceedings of the 2018 Robotics: Science and Systems, Pittsburgh, PA, USA, 26–30 June 2018; p. 59. [Google Scholar]
- Palomer, A.; Ridao, P.; Ribas, D.; Mallios, A.; Gracias, N.; Vallicrosa, G. Bathymetry-based SLAM with difference of normals point-cloud subsampling and probabilistic ICP registration. In Proceedings of the 2013 MTS/IEEE OCEANS-Bergen, Bergen, Norway, 10–14 June 2013; pp. 1–8. [Google Scholar]
- Trehard, G.; Alsayed, Z.; Pollard, E.; Bradai, B.; Nashashibi, F. Credibilist simultaneous localization and mapping with a lidar. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2699–2706. [Google Scholar]
- Arth, C.; Pirchheim, C.; Ventura, J.; Schmalstieg, D.; Lepetit, V. Instant Outdoor Localization and SLAM Initialization from 2.5D Maps. IEEE Trans. Vis. Comput. Graph. 2015, 21, 1309–1318. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, S.; Indelman, V.; Christensen, H.I.; Dellaert, F. Information-based reduced landmark SLAM. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4620–4627. [Google Scholar]
- Biber, P.; Straßer, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003)(Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003; pp. 2743–2748. [Google Scholar]
- Takeuchi, E.; Tsubouchi, T. A 3-D scan matching using improved 3-D normal distributions transform for mobile robotic mapping. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3068–3073. [Google Scholar]
- Magnusson, M. The Three-Dimensional Normal-Distributions Transform: An Efficient Representation for Registration, Surface Analysis, and Loop Detection. Ph.D. Dissertation, Örebro Universitet, Orebro, Sweden, 2009. [Google Scholar]
- Einhorn, E.; Gross, H.-M. Generic NDT mapping in dynamic environments and its application for lifelong SLAM. Robot. Auton. Syst. 2015, 69, 28–39. [Google Scholar] [CrossRef]
- Das, A.; Waslander, S.L. Scan registration using segmented region growing NDT. Int. J. Robot. Res. 2014, 33, 1645–1663. [Google Scholar] [CrossRef]
- Ye, H.; Chen, Y.; Liu, M. Tightly coupled 3d lidar inertial odometry and mapping. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3144–3150. [Google Scholar]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. Lio-sam: Tightly-coupled lidar inertial odometry via smoothing and mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 5135–5142. [Google Scholar]
- Wang, H.; Wang, C.; Chen, C.-L.; Xie, L. F-loam: Fast lidar odometry and mapping. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 4390–4396. [Google Scholar]
- Li, L.; Kong, X.; Zhao, X.; Li, W.; Wen, F.; Zhang, H.; Liu, Y. SA-LOAM: Semantic-aided LiDAR SLAM with loop closure. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 7627–7634. [Google Scholar]
- Chen, S.W.; Nardari, G.V.; Lee, E.S.; Qu, C.; Liu, X.; Romero, R.A.F.; Kumar, V. SLOAM: Semantic lidar odometry and mapping for forest inventory. IEEE Robot. Autom. Lett. 2019, 5, 612–619. [Google Scholar] [CrossRef] [Green Version]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE conference on computer vision and pattern recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Chen, X.-w.; Jeong, J.C. Enhanced recursive feature elimination. In Proceedings of the 2007 Sixth International Conference on Machine Learning and Applications, ICMLA 2007, Cincinnati, OH, USA, 13–15 December 2007; pp. 429–435. [Google Scholar]
- Wang, Y.; Dong, L.; Li, Y.; Zhang, H. Multitask feature learning approach for knowledge graph enhanced recommendations with RippleNet. PLoS ONE 2021, 16, e0251162. [Google Scholar] [CrossRef] [PubMed]


















| Sequence | 01 | 02 | 04 | 05 | 06 | 07 | 08 | 09 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| Scans | 1101 | 4661 | 271 | 2761 | 1101 | 1101 | 5171 | 1591 | 1201 |
| Trajectory length (m) | 2453 | 5067 | 393 | 2205 | 1232 | 694 | 3222 | 1705 | 919 |
| Loop closure (Y/N) | N | N | N | Y | Y | Y | Y | Y | N |
| Sequence | JLU_062801 | JLU_062802 | JLU_070101 | JLU_070102 |
|---|---|---|---|---|
| Scans | 3867 | 1648 | 7584 | 7779 |
| Trajectory length (m) | 754 | 382 | 1824 | 2044 |
| Loop closure (Y/N) | N | N | Y | Y |
| Method | LIO-SAM | LoNiC | |
|---|---|---|---|
| Sequence | |||
| 01 | 3.4853/0.0069 | 2.3651/0.0041 | |
| 02 | 1.9191/0.0054 | 2.1181/0.0057 | |
| 04 | 1.4769/0.0049 | 1.2080/0.0043 | |
| 05 | 0.6241/0.0037 | 0.6189/0.0038 | |
| 06 | 12.3343/0.0348 | 12.3265/0.0336 | |
| 07 | 0.5615/0.0040 | 0.7151/0.0059 | |
| 08 | 3.5843/0.0136 | 4.4680/0.0163 | |
| 09 | 1.9774/0.0063 | 1.4933/0.0049 | |
| 10 | 1.5089/0.0068 | 1.4544/0.0065 | |
| Average | 3.0524/0.0096 | 2.9742/0.0095 | |
| Method | LeGO-LOAM | LoNiC | |
|---|---|---|---|
| Sequence | |||
| 01 | 28.3265/0.0257 | 2.3651/0.0041 | |
| 02 | 10.6081/0.0108 | 2.1181/0.0057 | |
| 04 | 2.3260/0.0066 | 1.2080/0.0043 | |
| 05 | 2.1959/0.0056 | 0.6189/0.0038 | |
| 06 | 2.3439/0.0083 | 12.3265/0.0336 | |
| 07 | 1.6979/0.0068 | 0.7151/0.0059 | |
| 08 | 3.8719/0.0092 | 4.4680/0.0163 | |
| 09 | 8.3678/0.0078 | 1.4933/0.0049 | |
| 10 | 7.6577/0.0084 | 1.4544/0.0065 | |
| Average | 7.4884/0.0099 | 2.9742/0.0095 | |
| Method | LIO-SAM | LoNiC | |
|---|---|---|---|
| Sequence | |||
| JLU_062801 | 1.9931/0.0117 | 2.3454/0.0115 | |
| JLU_062802 | 3.3995/0.0214 | 2.1599/0.0085 | |
| JLU_070101 | 3.1710/0.0281 | 2.7353/0.0265 | |
| JLU_070102 | 4.6606/0.0247 | 4.2571/0.0225 | |
| Average | 3.3061/0.0215 | 2.8744/0.0173 | |
| Method | LIO-LOAM | LoNiC | |
|---|---|---|---|
| Sequence | |||
| JLU_062801 | 1.7278/0.0100 | 2.3454/0.0115 | |
| JLU_062802 | 4.1948/0.0269 | 2.1599/0.0085 | |
| JLU_070101 | 4.3408/0.0282 | 2.7353/0.0265 | |
| JLU_070102 | 5.7936/0.0268 | 4.2571/0.0225 | |
| Average | 4.0143/0.0230 | 2.8744/0.0173 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Gao, X.; Zhang, T.; Xu, Q.; Zhou, W. LiDAR Odometry and Mapping Based on Neighborhood Information Constraints for Rugged Terrain. Remote Sens. 2022, 14, 5229. https://doi.org/10.3390/rs14205229
Wang G, Gao X, Zhang T, Xu Q, Zhou W. LiDAR Odometry and Mapping Based on Neighborhood Information Constraints for Rugged Terrain. Remote Sensing. 2022; 14(20):5229. https://doi.org/10.3390/rs14205229
Chicago/Turabian StyleWang, Gang, Xinyu Gao, Tongzhou Zhang, Qian Xu, and Wei Zhou. 2022. "LiDAR Odometry and Mapping Based on Neighborhood Information Constraints for Rugged Terrain" Remote Sensing 14, no. 20: 5229. https://doi.org/10.3390/rs14205229
APA StyleWang, G., Gao, X., Zhang, T., Xu, Q., & Zhou, W. (2022). LiDAR Odometry and Mapping Based on Neighborhood Information Constraints for Rugged Terrain. Remote Sensing, 14(20), 5229. https://doi.org/10.3390/rs14205229