Modeling and Forecasting Ionospheric foF2 Variation in the Low Latitude Region during Low and High Solar Activity Years
Abstract
:1. Introduction
2. Materials and Methods
2.1. Ionospheric Data
2.2. Solar, Geomagnetic, Season, and Daily Cycle Index
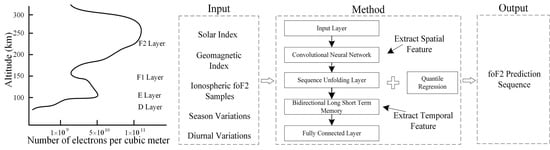
2.3. Hybrid Neural Network for Ionospheric Prediction
3. Results
3.1. Scenario 1: Analysis of Ionospheric foF2 Variation during Low Solar Activity Year (2010)
3.2. Scenario 2: Analysis of Ionospheric foF2 Variation during High Solar Activity Year (2014)
3.3. Prediction Analysis Results of Space Weather Events
3.3.1. Scenario 3: The foF2 Prediction Analysis for the 26 September 2011 Geomagnetic Storm
3.3.2. Scenario 4: The foF2 Prediction Analysis for the 15 July 2012 Geomagnetic Storm
4. Discussion
4.1. Analysis of Prediction Error Results
4.2. Analysis of Quantile Regression Weight
4.3. Analysis of Input and Output foF2 Time Series Length
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BiLSTM | Bidirectional long short-term memory |
| CNN | Convolutional neural network |
| LSTM | Long short-term memory |
| foF2 | Ionospheric F2 layer Critical frequency |
| IRI | International Reference Ionosphere |
| TEC | Total electron content |
| SSN | Sunspot number |
| UT | Universal time |
| F10.7 | Solar radio flux of 10.7 cm wavelength |
| IMF-Bz | Interplanetary magnetic field Bz component |
| Dst | Disturbance storm time |
| RNN | Recurrent neural network |
| QR | Quantile regression |
| RMSE | Root-mean-square error |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
References
- Bilitza, D.; Obrou, O.; Adeniyi, J.; Oladipo, O. Variability of foF2 in the equatorial ionosphere. Adv. Space Res. 2004, 34, 1901–1906. [Google Scholar] [CrossRef]
- Oyeyemi, E.O.; McKinnell, L.A.; Poole, A.W.V. Near-real time foF2 predictions using neural networks. J. Atmos. Sol. Terr. Phys. 2006, 68, 1807–1818. [Google Scholar] [CrossRef]
- Bai, H.; Feng, F.; Wang, J. A Combination Prediction Model of Long-Term Ionospheric foF2 Based on Entropy Weight Method. Entropy 2020, 22, 442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, C.; Wu, Z.S.; Xu, Z.W.; Sun, S.J.; Ding, Z.H.; Ban, P.P. Forecasting the local ionospheric foF2 parameter 1 hour ahead during disturbed geomagnetic conditions. J. Geophys. Res. Space Phys. 2010, 115, 135–146. [Google Scholar] [CrossRef]
- Olga, M. The Influence of Space Weather on the Relationship Between the Parameters TEC and foF2 of the Ionosphere. IEEE J. Radio Freq. Identif. 2021, 5, 261–268. [Google Scholar]
- Sun, W.; Long, X.; Xin, H. Forecasting of ionospheric vertical total electron content (TEC) using LSTM networks. In Proceedings of the 2017 International Conference on Machine Learning and Cybernetics (ICMLC), Ningbo, China, 9–12 July 2017 . [Google Scholar]
- Suin, M.; Yong, H.K.; Jeong, H.; Young, K.; Jong, Y. Forecasting the Ionospheric F2 Parameters over Jeju Station (33.43°N, 126.30°E) by Using Long Short-Term Memory. J. Korean Phys. Soc. 2020, 77, 1265–1273. [Google Scholar]
- Li, X.J.; Zhou, C.; Tang, Q.; Zhao, J.; Zhang, F.B.; Xia, G.C.; Liu, Y. Forecasting Ionospheric foF2 Based on Deep Learning Method. Remote Sensing 2021, 13, 3849. [Google Scholar] [CrossRef]
- Kim, J.H.; Kwak, Y.S.; Kim, Y.H.; Moon, S.I.; Jeong, S.H.; Yun, J.Y. Potential of Regional Ionosphere Prediction Using a Long Short-Term Memory Deep-Learning Algorithm Specialized for Geomagnetic Storm Period. Space Weather 2021, 19, 1–20. [Google Scholar] [CrossRef]
- Rao, T.V.; Sridhar, M.; Ratnam, D.V.; Harsha, P.B.S.; Srivani, I.A. Bidirectional Long Short-Term Memory-Based Ionospheric foF2 and hmF2 Models for a Single Station in the Low Latitude Region. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Williscroft, L.A.; Poole, A.W. Neural networks, foF2, sunspot number and magnetic activity. Geophys. Res. Lett. 1996, 23, 3659–3662. [Google Scholar] [CrossRef]
- McKinnell, L.A.; Poole, A.W.V. Ionospheric variability and electron density profile studies with neural networks. Adv. Space Res. 2001, 27, 83–90. [Google Scholar] [CrossRef]
- Athieno, R.; Jayachandran, P.T.; Themens, D.R. A neural network based foF2 model for a single station in the polar cap. Radio Sci. 2017, 52, 784–796. [Google Scholar] [CrossRef]
- Perna, L.; Pezzopane, M. foF2 vs solar indices for the Rome station: Looking for the best general relation which is able to describe the anomalous minimum between cycles 23 and 24. J. Atmos. Sol. Terr. Phys. 2016, 148, 13–21. [Google Scholar] [CrossRef] [Green Version]
- Joshua, E.O.; Nzekwe, N.M. foF2 correlation studies with solar and geomagnetic indices for two equatorial stations. J. Atmos. Sol. Terr. Phys. 2012, 80, 312–322. [Google Scholar] [CrossRef]
- Kane, R.P. Solar cycle variation of foF2. J. Atmos. Sol. Terr. Phys. 1994, 54, 1201–1205. [Google Scholar] [CrossRef]
- Bai, H.M.; Feng, F.; Jian, W.; Wu, T.S. Nonlinear dependence study of ionospheric F2 layer critical frequency with respect to the solar activity indices using the mutual information method. Adv. Space Res. 2019, 5, 1085–1092. [Google Scholar] [CrossRef]
- Campbell, W.H. Occurrence of AE and Dst geomagnetic index levels and the selection of the quietest days in a year. J. Geophys. Res. 1979, 84, 75–881. [Google Scholar]
- Ergen, T.; Kozat, S.S. Online Training of LSTM Networks in Distributed Systems for Variable Length Data Sequences. IEEE Trans. Neural. Netw. Learn. Syst. 2018, 29, 5159–5165. [Google Scholar] [CrossRef] [Green Version]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef] [Green Version]
- Mustaqeem Sajjad, M.; Kwon, S. Clustering-Based Speech Emotion Recognition by Incorporating Learned Features and Deep BiLSTM. IEEE Access 2020, 8, 79861–79875. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3285–3292. [Google Scholar]
- Kumar, S.D.; Subha, D. Prediction of Depression from EEG Signal Using Long Short Term Memory (LSTM). In Proceedings of the 2019 3rd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 23–25 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1248–1253. [Google Scholar]
- Zhang, X.; Zhang, Y.; Lu, X.; Bai, L.; Chen, L.; Tao, J.; Wang, Z.; Zhu, L. Estimation of Lower-Stratosphere-to-Troposphere Ozone Profile Using Long Short-Term Memory (LSTM). Remote Sens. 2021, 13, 1374. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K. Quantile Regression-An introduction. J. Econ. Perspect. 2000, 15, 143–156. [Google Scholar] [CrossRef]
- Zhang, W.; Quan, H.; Gandhi, O.; Rajagopal, R.; Tan, C.; Srinivasan, D. Improving Probabilistic Load Forecasting Using Quantile Regression NN With Skip Connections. IEEE Trans. Smart Grid. 2020, 11, 5442–5450. [Google Scholar] [CrossRef]
- Taylor, W. A Quantile Regression Neural Network Approach to Estimating the Conditional Density of Multiperiod Returns. J. Forecastin. 2020, 19, 299–311. [Google Scholar] [CrossRef]














| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |
|---|---|---|---|---|
| Time | January–December 2010 | January–December 2014 | 26 September 2011 | 15 July 2012 |
| Geomagnetic Activity | -- | -- | Storm (<−30 nT) | Storm (<−30 nT) |
| Season | -- | -- | Spring | Winter |
| Solar Activity | Low | High | High | High |
| Model Configuration | LSTM-foF2 | BiLSTM-foF2 |
|---|---|---|
| Learning Method | Deep Learning | Deep Learning |
| Numbers of Hidden Unit 1 | 250 | 250 |
| Numbers of Hidden Unit 2 | 250 | 250 |
| Epoch | 200 | 200 |
| Minimum Batch Size | 512 | 512 |
| Model Configuration | Summer | Autumn | Winter | Spring | |
|---|---|---|---|---|---|
| Season | 2010 | January | March | June | September |
| 2014 | January | March | June | September | |
| Smooth monthly values of SSN | 2010 | 14 | 18.5 | 24.6 | 29.5 |
| 2014 | 109.3 | 114.3 | 114.1 | 101.9 | |
| Model Configuration (January) | RMSE (MHz) | MAE (MHz) | MAPE |
|---|---|---|---|
| IRI-2016 | 0.801 | 0.643 | 12.286% |
| LSTM-foF2 | 0.904 | 0.692 | 13.193% |
| BiLSTM-foF2 | 0.871 | 0.678 | 12.618% |
| Proposed method | 0.77 | 0.60 | 11.802% |
| Model Configuration (March) | RMSE (MHz) | MAE (MHz) | MAPE |
|---|---|---|---|
| IRI-2016 | 1.123 | 0.935 | 15.478% |
| LSTM-foF2 | 1.033 | 0.788 | 12.971% |
| BiLSTM-foF2 | 0.986 | 0.782 | 12.671% |
| Proposed method | 0.878 | 0.701 | 12.468% |
| Model Configuration (June) | RMSE (MHz) | MAE (MHz) | MAPE |
|---|---|---|---|
| IRI-2016 | 0.648 | 0.527 | 11.99% |
| LSTM-foF2 | 0.947 | 0.745 | 19.29% |
| BiLSTM-foF2 | 0.754 | 0.592 | 14.529% |
| Proposed method | 0.583 | 0.46 | 10.24% |
| Model Configuration (September) | RMSE (MHz) | MAE (MHz) | MAPE |
|---|---|---|---|
| IRI-2016 | 0.811 | 0.654 | 12.482% |
| LSTM-foF2 | 0.979 | 0.777 | 13.832% |
| BiLSTM-foF2 | 0.8 | 0.627 | 12.005% |
| Proposed method | 0.688 | 0.542 | 10.608% |
| Model Configuration (January) | RMSE (MHz) | MAE (MHz) | MAPE |
|---|---|---|---|
| IRI-2016 | 1.05 | 0.851 | 10.26% |
| LSTM-foF2 | 1.03 | 0.812 | 9.763% |
| BiLSTM-foF2 | 0.959 | 0.767 | 9.52% |
| Proposed method | 0.837 | 0.669 | 8.183% |
| Model Configuration (March) | RMSE (MHz) | MAE (MHz) | MAPE |
|---|---|---|---|
| IRI-2016 | 1.582 | 1.451 | 15.442% |
| LSTM-foF2 | 1.816 | 1.527 | 15.812% |
| BiLSTM-foF2 | 1.808 | 1.577 | 16.106% |
| Proposed method | 1.262 | 0.998 | 10.356% |
| Model Configuration (June) | RMSE (MHz) | MAE (MHz) | MAPE |
|---|---|---|---|
| IRI-2016 | 1.163 | 0.96 | 16.99% |
| LSTM-foF2 | 1.42 | 1.104 | 22.656% |
| BiLSTM-foF2 | 1.16 | 0.945 | 17.643% |
| Proposed method | 0.778 | 0.626 | 11.684% |
| Model Configuration (October) | RMSE (MHz) | MAE (MHz) | MAPE |
|---|---|---|---|
| IRI-2016 | 1.281 | 1.054 | 14.667% |
| LSTM-foF2 | 1.134 | 0.911 | 12.847% |
| BiLSTM-foF2 | 1.06 | 0.844 | 11.961% |
| Proposed method | 0.837 | 0.644 | 8.969% |
| Model Configuration | RMSE (MHZ) | MAE (MHZ) | MAPE |
|---|---|---|---|
| IRI-2016 | 1.059 | 0.865 | 13.5% |
| LSTM-foF2 | 1.373 | 1.017 | 14.86% |
| BiLSTM-foF2 | 1.035 | 0.814 | 11.587% |
| Proposed method | 0.966 | 0.784 | 11.181% |
| Model Configuration | RMSE (MHZ) | MAE (MHZ) | MAPE |
|---|---|---|---|
| IRI-2016 | 2.057 | 1.760 | 37.427% |
| LSTM-foF2 | 1.61 | 1.306 | 31.802% |
| BiLSTM-foF2 | 1.496 | 1.207 | 27.364% |
| Proposed method | 1.265 | 0.996 | 22.737% |
| Quartiles Weight | RMSE (MHZ) | MAE (MHZ) | MAPE |
|---|---|---|---|
| 0.25 | 1.33 | 1.11 | 17.65% |
| 0.5 | 0.98 | 0.77 | 12.77% |
| 0.75 | 0.86 | 0.67 | 11.95% |
| Quartiles Weight | RMSE (MHZ) | MAE (MHZ) | MAPE |
|---|---|---|---|
| 0.25 | 1.4 | 1.13 | 12.89% |
| 0.5 | 1.21 | 0.96 | 10.85% |
| 0.75 | 1.05 | 0.81 | 9.56% |
| Input Time Series Length | Training Samples (Input) | Validation Samples | Test/Predict Samples (Output) |
|---|---|---|---|
| One month | December 2009 | January 2010 | February 2010 |
| Three months | October–December 2009 | January 2010 | February 2010 |
| Six months | July–December 2009 | January 2010 | February 2010 |
| Nine months | April–December 2009 | January 2010 | February 2010 |
| Full | January–December 2009 | January 2010 | February 2010 |
| Input Time Series Length | RMSE (MHZ) | MAE (MHZ) | MAPE |
|---|---|---|---|
| One month | 1.80 | 1.54 | 24.52% |
| Three months | 1.49 | 1.23 | 19.84% |
| Six months | 1.14 | 0.87 | 14.28% |
| Nine months | 0.93 | 0.73 | 12.2% |
| Full | 0.86 | 0.67 | 11.95% |
| Output Time Series Length | Training Samples (Input) | Validation Samples | Test/Predict Samples (Output) |
|---|---|---|---|
| One month | January–December 2009 | January 2010 | February 2010 |
| Three months | January–December 2009 | January 2010 | February–April 2010 |
| Six months | January–December 2009 | January 2010 | February–July 2010 |
| Nine months | January–December 2009 | January 2010 | February–October 2010 |
| Twelve months | January–December 2009 | January 2010 | February 2010–January 2011 |
| Output Time Series Length | RMSE (MHZ) | MAE (MHZ) | MAPE |
|---|---|---|---|
| One month | 0.86 | 0.67 | 11.95% |
| Three months | 0.88 | 0.68 | 13.16% |
| Six months | 0.92 | 0.7 | 14.81% |
| Nine months | 0.93 | 0.72 | 15.9% |
| Twelve months | 1 | 0.79 | 16.05% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, C.; Ren, P.; Yin, T.; Xiang, Z.; Zhang, Y. Modeling and Forecasting Ionospheric foF2 Variation in the Low Latitude Region during Low and High Solar Activity Years. Remote Sens. 2022, 14, 5418. https://doi.org/10.3390/rs14215418
Bi C, Ren P, Yin T, Xiang Z, Zhang Y. Modeling and Forecasting Ionospheric foF2 Variation in the Low Latitude Region during Low and High Solar Activity Years. Remote Sensing. 2022; 14(21):5418. https://doi.org/10.3390/rs14215418
Chicago/Turabian StyleBi, Cheng, Peng Ren, Ting Yin, Zheng Xiang, and Yang Zhang. 2022. "Modeling and Forecasting Ionospheric foF2 Variation in the Low Latitude Region during Low and High Solar Activity Years" Remote Sensing 14, no. 21: 5418. https://doi.org/10.3390/rs14215418
APA StyleBi, C., Ren, P., Yin, T., Xiang, Z., & Zhang, Y. (2022). Modeling and Forecasting Ionospheric foF2 Variation in the Low Latitude Region during Low and High Solar Activity Years. Remote Sensing, 14(21), 5418. https://doi.org/10.3390/rs14215418