Comparison on Quantitative Analysis of Olivine Using MarSCoDe Laser-Induced Breakdown Spectroscopy in a Simulated Martian Atmosphere
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Samples and Experiment Environment
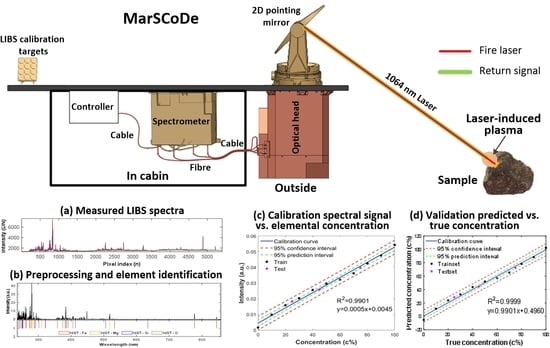
2.1.1. Instrument Description and Simulated Experiment
2.1.2. Sample Pretreatment and Component Content
2.2. Preprocessing of LIBS Spectra
2.2.1. Noise and Background Removal
- (1)
- Subtracting background
- (2)
- Denoising random signal
- (3)
- Removing continuum baseline
2.2.2. Wavelength and Radiation Calibration
- (1)
- Spectral drift correction and wavelength calibration
- (2)
- Radiation calibration on the respond
2.2.3. Merging and Normalization
- (1)
- Merge multi-channel into complete spectrum
- (2)
- Normalization of the spectra
2.3. Quantitative Analysis and Evaluation
2.3.1. Quantitative Analysis
- (1)
- Calibration curve with linear regression and multivariate linear regression
- (2)
- Ridge, LASSO, and Elastic Net
- (3)
- PCR and PLSR
- (4)
- Back-propagation
2.3.2. Evaluation and Validation
3. Results and Discussion
3.1. Pretreatments of LIBS Spectra Preprocessing
3.2. Calibration and Validation of Quantitative Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, W.M.; Liu, X.F.; Yan, Z.X.; Li, L.N.; Zhang, Z.Q.; Kuang, Y.W.; Jiang, H.; Yu, H.X.; Yang, F.; Liu, C.F.; et al. The MarSCoDe instrument suite on the Mars rover of China’s Tianwen-1 mission. Space Sci. Rev. 2021, 217, 58. [Google Scholar] [CrossRef]
- Geng, Y.; Zhou, J.; Li, S.; Fu, Z.; Meng, L.; Liu, J.; Wang, H. A brief introduction of the first Mars exploration mission in China. J. Deep Space Explor. 2018, 5, 399–405. [Google Scholar]
- Li, C.; Liu, J.; Geng, Y.; Cao, J.; Zhang, T.; Fang, G.; Yang, J.; Shu, R.; Zou, Y.; Lin, Y.; et al. Scientific objectives and payload configuration of China’s first Mars exploration mission. J. Deep Space Explor. 2018, 5, 406–413. [Google Scholar]
- Jia, Y.Z.; Fan, Y.; Zou, Y.L. Scientific objectives and payloads of Chinese first Mars exploration. Chin. J. Space Sci. 2018, 38, 650–655. [Google Scholar]
- Zou, Y.; Zhu, Y.; Bai, Y.; Wang, L.; Jia, Y.; Shen, W.; Fan, Y.; Liu, Y.; Wang, C.; Zhang, A.; et al. Scientific objectives and payloads of Tianwen-1, China’s first Mars exploration mission. Adv. Space Res. 2021, 67, 812–823. [Google Scholar] [CrossRef]
- Harmon, R.S.; Remus, J.; McMillan, N.J.; McManus, C.; Collins, L.; Gottfried, J.L., Jr.; DeLucia, F.; Miziolek, A.W. LIBS analysis of geomaterials: Geochemical fingerprinting for the rapid analysis and discrimination of minerals. Appl. Geochem. 2009, 24, 1125–1141. [Google Scholar] [CrossRef]
- Harmon, R.S.; Russo, R.E.; Hark, R.R. Applications of laser-induced breakdown spectroscopy for geochemical and environmental analysis: A comprehensive review. Spectrochim. Acta Part B At. Spectrosc. 2013, 87, 11–26. [Google Scholar] [CrossRef]
- Markiewicz-Keszycka, M.; Cama-Moncunill, X.; Casado-Gavalda, M.P.; Dixit, Y.; Cama-Moncunill, R.; Cullen, P.J.; Sullivan, C. Laser-induced breakdown spectroscopy (LIBS) for food analysis: A review. Trends Food Sci. Technol. 2017, 65, 80–93. [Google Scholar] [CrossRef]
- Sobron, P.; Wang, A.; Sobron, F. Extraction of compositional and hydration information of sulfates from laser-induced plasma spectra recorded under Mars atmospheric conditions—Implications for ChemCam investigations on Curiosity rover. Spectrochim. Acta Part B At. Spectrosc. 2012, 68, 1–16. [Google Scholar] [CrossRef]
- Wiens, R.C.; Maurice, S.; Lasue, J.; Forni, O.; Anderson, R.B.; Clegg, S.; Bender, S.; Blaney, D.; Barraclough, B.L.; Cousin, A.; et al. Pre-flight calibration and initial data processing for the ChemCam laser-induced breakdown spectroscopy instrument on the Mars Science Laboratory rover. Spectrochim. Acta Part B At. Spectrosc. 2013, 82, 1–27. [Google Scholar] [CrossRef]
- Brech, F.; Cross, L. Abstracts of Xth colloquium spectroscopicum international and first meeting of the society for applied spectroscopy. Appl. Spectrosc. 1962, 16, 59. [Google Scholar]
- Cremers, D.A. The analysis of metals at a distance using laser induced breakdown spectroscopy. Appl. Spectrosc. 1987, 41, 572–578. [Google Scholar] [CrossRef]
- Rohwetter, P.; Stelmaszczyk, K.; Wöste, L.; Ackermann, R.; Méjean, G.; Salmon, E.; Kasparian, J.; Yu, J.; Wolf, J.-P. Filament-induced remote surface ablation for long range laser-induced breakdown spectroscopy operation. Spectrochim. Acta Part B At. Spectrosc. 2005, 60, 1025–1033. [Google Scholar] [CrossRef]
- Blacic, J.D.; Petit, D.R.; Cremers, D.A.; Roessler, N. Laser-induced breakdown spectroscopy for remote elemental analysis of planetary surfaces. In Proceedings of the International symposium on spectral sensing research, Maui, HI, USA, 15–20 November 1992; pp. 302–312. [Google Scholar]
- Wiens, R.C.; Arvidson, R.E.; Cremers, D.A.; Ferris, M.J.; Blacic, J.D.; Seelos, F.P., IV; Deal, K.S. Combined remote mineralogical and elemental identification from rovers: Field and laboratory tests using reflectance and laser-induced breakdown spectroscopy. J. Geophys. Res. 2002, 107, FIDO 3-1–FIDO 3-14. Available online: https://agupubs.onlinelibrary.wiley.com/doi/epdf/10.1029/2000JE001439 (accessed on 9 October 2022). [CrossRef]
- Cousin, A.; Forni, O.; Maurice, S.; Gasnault, O.; Fabre, C.; Sautter, V.; Wiens, R.C.; Mazoyer, J. Laser induced breakdown spectroscopy library for the Martian environment. Spectrochim. Acta Part B At. Spectrosc. 2011, 66, 805–814. [Google Scholar] [CrossRef]
- Wiens, R.C.; Maurice, S.; Barraclough, B.; Saccoccio, M.; Barkley, W.C.; Bell III, J.F.; Bender, S.; Bernardin, J.; Blaney, D.; Blank, J.; et al. The ChemCam Instrument Suite on the Mars Science Laboratory (MSL) Rover: Body Unit and Combined System Tests. Space Sci. Rev. 2012, 170, 167–227. [Google Scholar] [CrossRef]
- Maurice, S.; Wiens, R.C.; Saccoccio, M.; Barraclough, B.; Gasnault, O.; Forni, O.; Mangold, N.; Baratoux, D.; Bender, S.; Berger, G.; et al. The ChemCam instrument suite on the Mars Science Laboratory (MSL) rover: Science objectives and mast unit description. Space Sci. Rev. 2012, 170, 95–166. [Google Scholar] [CrossRef]
- Clegg, S.M.; Wiens, R.C.; Anderson, R.; Forni, O.; Frydenvang, J.; Lasue, J.; Cousin, A.; Payré, V.; Boucher, T.; Dyar, M.D.; et al. Recalibration of the Mars Science Laboratory ChemCam instrument with an expanded geochemical database. Spectrochim. Acta Part B At. Spectrosc. 2017, 129, 64–85. [Google Scholar] [CrossRef]
- Wiens, R.C.; Maurice, S.; Robinson, S.H.; Nelson, A.E.; Cais, P.; Bernardi, P.; Newell, R.T.; Clegg, S.; Sharma, S.K.; Storms, S.; et al. The SuperCam instrument suite on the NASA Mars 2020 rover: Body unit and combined system tests. Space Sci. Rev. 2021, 217, 4. [Google Scholar] [CrossRef]
- Maurice, S.; Wiens, R.C.; Bernardi, P.; Caïs, P.; Robinson, S.; Nelson, T.; Gasnault, O.; Reess, J.-M.; Deleuze, M.; Rull, F.; et al. The SuperCam instrument suite on the Mars 2020 rover: Science objectives and mast-unit description. Space Sci. Rev. 2021, 217, 47. [Google Scholar] [CrossRef]
- Anderson, R.B.; Forni, O.; Cousin, A.; Wiens, R.C.; Clegg, S.M.; Frydenvang, J.; Gabriel, T.S.J.; Ollila, A.; Schröder, S.; Beyssac, O.; et al. Post-landing major element quantification using SuperCam laser induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2022, 188, 106347. [Google Scholar] [CrossRef]
- Boucher, T.F.; Ozanne, M.V.; Carmosino, M.L.; Dyar, M.D.; Mahadevan, S.; Breves, E.A.; Lepore, K.H.; Clegg, S.M. A study of machine learning regression methods for major elemental analysis of rocks using laser-induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2015, 107, 1–10. [Google Scholar] [CrossRef]
- Takahashi, T.; Thornton, B. Quantitative methods for compensation of matrix effects and self-absorption in Laser Induced Breakdown Spectroscopy signals of solids. Spectrochim. Acta Part B At. Spectrosc. 2017, 138, 31–42. [Google Scholar] [CrossRef]
- Tucker, J.M.; Dyar, M.D.; Schaefer, M.W.; Clegg, S.M.; Wiens, R.C. Optimization of laser-induced breakdown spectroscopy for rapid geochemical analysis. Chem. Geol. 2010, 277, 137–148. [Google Scholar] [CrossRef]
- Doucet, F.R.; Belliveau, T.F.; Fortier, J.-L.; Hubert, J. Use of chemometrics and laser induced breakdown spectroscopy for quantitative analysis of major and minor elements in aluminium alloys. Appl. Spectrosc. 2007, 61, 327–332. [Google Scholar] [CrossRef]
- Andrade, J.M.; Cristoforetti, G.; Legnaioli, S.; Lorenzetti, G.; Palleschi, V.; Shaltout, A.A. Classical univariate calibration and partial least squares for quantitative analysis of brass samples by laser-induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2010, 65, 658–663. [Google Scholar] [CrossRef]
- Dyar, M.D.; Carmosino, M.L.; Breves, E.A.; Ozanne, M.V.; Clegg, S.M.; Wiens, R.C. Comparison of partial least squares and lasso regression techniques as applied to laser-induced breakdown spectroscopy of geological samples. Spectrochim. Acta Part B At. Spectrosc. 2012, 70, 51–67. [Google Scholar] [CrossRef]
- El Haddad, J.; Canioni, L.; Bousquet, B. Good practices in LIBS analysis: Review and advices. Spectrochim. Acta Part B At. Spectrosc. 2014, 101, 171–182. [Google Scholar] [CrossRef] [Green Version]
- Mukhono, P.M.; Angeyo, K.H.; Dehayem-Kamadjeu, A.; Kaduki, K.A. Laser induced breakdown spectroscopy and characterization of environmental matrices utilizing multivariate chemometrics. Spectrochim. Acta Part B At. Spectrosc. 2013, 87, 81–85. [Google Scholar] [CrossRef]
- Bricklemyer, R.S.; Brown, D.J.; Turk, P.J.; Clegg, S.M. Improved intact soil–core carbon determination applying regression shrinkage and variable selection techniques to complete spectrum laser-induced breakdown spectroscopy (LIBS). Appl. Spectrosc. 2013, 67, 1185–1199. [Google Scholar] [CrossRef]
- Sirven, J.B.; Bousquet, B.; Canioni, L.; Sarger, L.; Tellier, S.; Potin-Gautier, M.; Hecho, I.L. Qualitative and quantitative investigation of chromium-polluted soils by laser induced breakdown spectroscopy combined with neural networks analysis. Anal. Bioanal. Chem. 2006, 385, 256–262. [Google Scholar] [CrossRef] [PubMed]
- El Haddad, J.; Villot-Kadri, M.; Ismaël, A.; Gallou, G.; Michel, K.; Bruyère, D.; Laperche, V.; Canioni, L.; Bousquet, B. Artificial neural network for on-site quantitative analysis of soils using laser induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2013, 79–80, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Anderson, R.B.; Bell III, J.F.; Wiens, R.C.; Morris, R.V.; Clegg, S.M. Clustering and training set selection methods for improving the accuracy of quantitative laser induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2012, 70, 24–32. [Google Scholar] [CrossRef]
- Kaski, S.; Häkkänen, H.; Korppi-Tommola, J. Laser-induced plasma spectroscopy to as low as 130 nm when a gas-purged spectrograph and ICCD detection are used. Appl. Opt. 2003, 42, 6036–6039. [Google Scholar] [CrossRef]
- Radziemski, L.J.; Cremers, D.A.; Bostian, M.; Chinni, R.C.; Navarro-Northrup, C. Laser-Induced Breakdown Spectra in the Infrared Region from 750 to 2000 nm Using a Cooled InGaAs Diode Array Detector. Appl. Spectrosc. 2007, 61, 1141–1146. [Google Scholar] [CrossRef] [PubMed]
- Tognoni, E.; Cristoforetti, G. [INVITED] Signal and noise in laser induced breakdown spectroscopy: An introductory review. Opt. Laser Technol. 2016, 79, 164–172. [Google Scholar] [CrossRef]
- Bastiaans, G.; Mangold, R. The calculation of electron density and temperature in Ar spectroscopic plasmas from continuum and line spectra. Spectrochim. Acta Part B At. Spectrosc. 1985, 40, 885–892. [Google Scholar] [CrossRef]
- Cremers, D.A.; Radziemski, L.J. Handbook of Laser-Induced Breakdown Spectroscopy; John Wiley & Sons: Chichester, UK; Hoboken, NJ, USA, 2006. [Google Scholar]
- Sobron, P.; Sobron, F.; Sanz, A.; Rull, F. Raman signal processing software for automated identification of mineral phases and biosignatures on Mars. Appl. Spectrosc. 2008, 62, 364–370. [Google Scholar] [CrossRef]
- Baek, S.-J.; Park, A.; Ahn, Y.-J.; Choo, J. Baseline correction using asymmetrically reweighted penalized least squares smoothing. Analyst 2015, 140, 250–257. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, A.; Karki, V.; Aggarwal, S.K.; Maurya, G.S.; Kumar, R.; Rai, A.K.; Mao, X.; Russo, R.E. Evaluation of the prediction precision capability of partial least squares regression approach for analysis of high alloy steel by laser induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2015, 108, 8–14. [Google Scholar] [CrossRef]
- Karki, V.; Sarkar, A.; Singh, M.; Maurya, G.S.; Kumar, R.; Rai, A.K.; Aggarwal, S.K. Comparison of spectrum normalization techniques for univariate analysis of stainless steel by laser-induced breakdown spectroscopy. Pramana J. Phys. 2016, 86, 1313–1327. [Google Scholar] [CrossRef]
- Castro, J.P.; Pereira-Filho, E.R. Twelve different types of data normalization for the proposition of classification, univariate and multivariate regression models for the direct analyses of alloys by laser-induced breakdown spectroscopy (LIBS). J. Anal. At. Spectrom. 2016, 31, 2005–2014. [Google Scholar] [CrossRef]
- Fu, H.; Jia, J.; Wang, H.; Ni, Z.; Dong, F. Calibration Methods of Laser-Induced Breakdown Spectroscopy. In Calibration and Validation of Analytical Methods—A Sampling of Current Approaches; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef] [Green Version]
- Martens, H.; Naes, T. Multivariate Calibration; John Wiley & Sons: Chichester, UK, 1991. [Google Scholar]
- Martin, M.Z.; Labbe, N.; Rials, T.G.; Wullschleger, S.D. Analysis of preservative-treated wood by multivariate analysis of laser-induced breakdown spectroscopy spectra. Spectrochim. Acta Part B At. Spectrosc. 2005, 60, 1179–1185. [Google Scholar] [CrossRef]
- Grebneva-Balyuk, O.N. A new method for finding the limits of quantification of elements, estimating dynamic range, and detecting matrix and interelement interferences in spectral analysis (atomic absorption spectrometry and ICP analysis methods). J. Anal. Chem. 2022, 77, 66–80. [Google Scholar] [CrossRef]
- Boumans, P. Detection limits and spectral interferences in atomic emission spectrometry. Anal. Chem. 1994, 66, 459–467. [Google Scholar] [CrossRef]








| Items | Values |
|---|---|
| Stand-off distance | 1.6–7 m |
| Laser type | Nd:YAG |
| Laser wavelength | 1064 nm |
| Pulse width | 4 ns |
| Laser energy | 23 mJ |
| Pulse frequency | 1, 2, 3 Hz |
| Pulse energy density | 200 MW/mm2 @ 2 m32 MW/mm2 @ 5 m |
| Spectral range | 240.00–850.00 nm |
| Spectral sampling interval | 0.067 nm @ 240–340 nm |
| 0.132 nm @ 340–540 nm | |
| 0.203 nm @ 540–850 nm |
| Samples | Mg2SiO4 (Fo) | Fe2SiO4 (Fa) | MgO | Fe2O3 | SiO2 | |
|---|---|---|---|---|---|---|
| Content/c% | Proportional Coefficient of Moles Content | |||||
| Training | A01 | 0 | 100 | 0 | 100 | 100 |
| A02 | 10 | 90 | 20 | 90 | 100 | |
| A03 | 20 | 80 | 40 | 80 | 100 | |
| A04 | 30 | 70 | 60 | 70 | 100 | |
| A05 | 40 | 60 | 80 | 60 | 100 | |
| A06 | 50 | 50 | 100 | 50 | 100 | |
| A07 | 60 | 40 | 120 | 40 | 100 | |
| A08 | 70 | 30 | 140 | 30 | 100 | |
| A09 | 80 | 20 | 160 | 20 | 100 | |
| A10 | 90 | 10 | 180 | 10 | 100 | |
| A11 | 100 | 0 | 200 | 0 | 100 | |
| Test | T01 | 25 | 75 | 50 | 75 | 100 |
| T02 | 55 | 45 | 110 | 45 | 100 | |
| T03 | 75 | 25 | 150 | 25 | 100 | |
| Item | Fo | Fa | ||
|---|---|---|---|---|
| Mean Spectrum | All Spectra | Mean Spectrum | All Spectra | |
| R2_train | 0.9650 | 0.9615 | 0.9901 | 0.9829 |
| R2_test | 0.9466 | 0.9386 | 0.9839 | 0.9737 |
| MAE_train (c%) | 5.3633 | 5.4351 | 2.8993 | 3.4161 |
| MAE_test (c%) | 4.4533 | 4.5612 | 2.3015 | 2.6759 |
| RMSE_train (c%) | 5.9131 | 6.2079 | 3.1495 | 4.1358 |
| RMSE_test (c%) | 4.7486 | 5.0935 | 2.6056 | 3.3337 |
| Std_train (c%) | 5.9131 | 6.2079 | 3.1495 | 4.1358 |
| Std_test (c%) | 1.6485 | 2.4202 | 2.6036 | 3.3337 |
| LOD (c%) | 0.9943 | 2.3354 | 2.0536 | 3.8883 |
| Data Source | Methods | R2 | MAE (c%) | RMSE (c%) | Std (c%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | |||
| Fo calibration | Mean spectrum | MLR | 0.9888 | 0.9712 | 2.4502 | 2.8176 | 3.3454 | 3.4870 | 3.3454 | 3.3930 |
| Ridge | 0.9915 | 0.6335 | 2.5350 | 11.8251 | 2.9094 | 12.4391 | 2.9094 | 12.2429 | ||
| LASSO | 0.9919 | 0.9168 | 2.4495 | 4.8005 | 2.8381 | 5.9268 | 2.8381 | 5.8816 | ||
| Elastic Net | 0.9926 | 0.9573 | 2.3732 | 3.6437 | 2.7153 | 4.2448 | 2.7153 | 4.2294 | ||
| PCR | 0.9978 | 0.9962 | 1.1177 | 1.2100 | 1.4731 | 1.2706 | 1.4731 | 1.1350 | ||
| PLSR | 1.0000 | 0.9958 | 0.0000 | 1.0242 | 0.0000 | 1.3313 | 0.0000 | 0.8505 | ||
| BP | 0.8930 | 0.6320 | 5.9867 | 11.7907 | 10.3428 | 12.4648 | 10.0868 | 4.0438 | ||
| All spectra | MLR | 0.9751 | 0.8930 | 3.7925 | 5.6764 | 4.9931 | 6.7221 | 4.9931 | 6.6167 | |
| Ridge | 0.9950 | 0.9456 | 1.7865 | 4.2160 | 2.2281 | 4.7936 | 2.2281 | 4.3511 | ||
| LASSO | 0.9983 | 0.9899 | 0.9774 | 1.7033 | 1.3178 | 2.0640 | 1.3178 | 1.9793 | ||
| Elastic Net | 0.9983 | 0.9889 | 0.9403 | 1.8355 | 1.2856 | 2.1623 | 1.2856 | 2.0697 | ||
| PCR | 0.9945 | 0.9910 | 1.8679 | 1.5385 | 2.3350 | 1.9465 | 2.3350 | 1.8932 | ||
| PLSR | 0.9994 | 0.9923 | 0.5814 | 1.4683 | 0.7457 | 1.8087 | 0.7457 | 1.8067 | ||
| BP | 0.9965 | 0.9696 | 0.7422 | 6.4056 | 1.8700 | 8.3740 | 1.8692 | 6.0885 | ||
| Fa calibration | Mean spectrum | MLR | 0.9932 | 0.8981 | 2.2134 | 6.4493 | 2.6053 | 6.5605 | 2.6053 | 6.3726 |
| Ridge | 0.9904 | 0.6185 | 2.7046 | 12.0484 | 3.0910 | 12.6919 | 3.0910 | 12.5018 | ||
| LASSO | 0.9919 | 0.9168 | 2.4495 | 4.8005 | 2.8381 | 5.9268 | 2.8381 | 5.8816 | ||
| Elastic Net | 0.9964 | 0.9656 | 1.6474 | 3.3251 | 1.9016 | 3.8095 | 1.9016 | 3.7957 | ||
| PCR | 0.9978 | 0.9962 | 1.1177 | 1.2100 | 1.4731 | 1.2706 | 1.4731 | 1.1350 | ||
| PLSR | 1.0000 | 0.9958 | 0.0000 | 1.0242 | 0.0000 | 1.3313 | 0.0000 | 0.8505 | ||
| BP | 0.8852 | −1.7729 | 5.4088 | 27.1768 | 10.7164 | 34.2169 | 9.2513 | 29.9132 | ||
| All spectra | MLR | 0.9932 | 0.8981 | 2.2134 | 6.4493 | 2.6053 | 6.5605 | 2.6053 | 6.3726 | |
| Ridge | 0.9904 | 0.6185 | 2.7046 | 12.0484 | 3.0910 | 12.6919 | 3.0910 | 12.5018 | ||
| LASSO | 0.9919 | 0.9168 | 2.4495 | 4.8005 | 2.8381 | 5.9268 | 2.8381 | 5.8816 | ||
| Elastic Net | 0.9964 | 0.9656 | 1.6474 | 3.3251 | 1.9016 | 3.8095 | 1.9016 | 3.7957 | ||
| PCR | 0.9978 | 0.9962 | 1.1177 | 1.2100 | 1.4731 | 1.2706 | 1.4731 | 1.1350 | ||
| PLSR | 1.0000 | 0.9958 | 0.0000 | 1.0242 | 0.0000 | 1.3313 | 0.0000 | 0.8505 | ||
| BP | 0.8852 | −1.7729 | 5.4088 | 27.1768 | 10.7164 | 34.2169 | 9.2513 | 29.9132 | ||
| Data Source | Methods | R2 | MAE (c%) | RMSE (c%) | Std (c%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | |||
| Fo validation | Mean spectrum | MLR | 0.9999 | 0.9999 | 0.3052 | 0.2052 | 0.3539 | 0.2307 | 0.3539 | 0.2300 |
| Ridge | 0.9948 | 0.9947 | 1.9739 | 1.3269 | 2.2887 | 1.4921 | 2.2887 | 1.4872 | ||
| LASSO | 0.9920 | 0.9920 | 2.4334 | 1.6358 | 2.8216 | 1.8394 | 2.8216 | 1.8334 | ||
| ElasticNet | 0.9930 | 0.9929 | 2.2828 | 1.5346 | 2.6469 | 1.7256 | 2.6469 | 1.7199 | ||
| PCR | 1.0000 | 1.0000 | 0.0592 | 0.0398 | 0.0686 | 0.0447 | 0.0686 | 0.0446 | ||
| PLSR | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||
| BP | 0.9941 | 0.9864 | 2.2873 | 2.3309 | 2.4328 | 2.3923 | 0.8288 | 0.5386 | ||
| All spectra | MLR | 0.9994 | 0.9994 | 3.7925 | 5.6764 | 0.7884 | 0.5140 | 0.7884 | 0.5123 | |
| Ridge | 0.9991 | 0.9991 | 0.8150 | 0.5479 | 0.9450 | 0.6161 | 0.9450 | 0.6141 | ||
| LASSO | 0.9999 | 0.9999 | 0.3096 | 0.2081 | 0.3589 | 0.2340 | 0.3589 | 0.2332 | ||
| Elastic Net | 0.9999 | 0.9999 | 0.2386 | 0.1604 | 0.2767 | 0.1804 | 0.2767 | 0.1798 | ||
| PCR | 1.0000 | 1.0000 | 0.1487 | 0.1000 | 0.1724 | 0.1124 | 0.1724 | 0.1120 | ||
| PLSR | 1.0000 | 1.0000 | 0.0152 | 0.0102 | 0.0176 | 0.0115 | 0.0176 | 0.0114 | ||
| BP | 1.0000 | 1.0000 | 0.0541 | 0.0539 | 0.0543 | 0.0540 | 0.0040 | 0.0026 | ||
| Fa validation | Mean spectrum | MLR | 1.0000 | 1.0000 | 0.1851 | 0.1244 | 0.2146 | 0.1399 | 0.2146 | 0.1395 |
| Ridge | 0.9939 | 0.9938 | 2.1385 | 1.4375 | 2.4796 | 1.6165 | 2.4796 | 1.6112 | ||
| LASSO | 0.9920 | 0.9920 | 2.4334 | 1.6358 | 2.8216 | 1.8394 | 2.8216 | 1.8334 | ||
| Elastic Net | 0.9967 | 0.9966 | 1.5764 | 1.0597 | 1.8279 | 1.1916 | 1.8279 | 1.1877 | ||
| PCR | 1.0000 | 1.0000 | 0.0592 | 0.0398 | 0.0686 | 0.0447 | 0.0686 | 0.0446 | ||
| PLSR | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||
| BP | 0.9441 | 0.9108 | 6.1141 | 5.1367 | 7.4780 | 6.1355 | 5.1638 | 3.3554 | ||
| All spectra | MLR | 1.0000 | 1.0000 | 1.2767 | 1.7129 | 0.0922 | 0.0601 | 0.0922 | 0.0599 | |
| Ridge | 0.9992 | 0.9992 | 0.7544 | 0.5071 | 0.8747 | 0.5703 | 0.8747 | 0.5684 | ||
| LASSO | 0.9999 | 0.9999 | 0.2856 | 0.1920 | 0.3312 | 0.2159 | 0.3312 | 0.2152 | ||
| Elastic Net | 0.9999 | 0.9999 | 0.2581 | 0.1735 | 0.2993 | 0.1951 | 0.2993 | 0.1945 | ||
| PCR | 1.0000 | 1.0000 | 0.1487 | 0.1000 | 0.1724 | 0.1124 | 0.1724 | 0.1120 | ||
| PLSR | 1.0000 | 1.0000 | 0.0152 | 0.0102 | 0.0176 | 0.0115 | 0.0176 | 0.0114 | ||
| BP | 1.0000 | 1.0000 | 0.0807 | 0.0782 | 0.0929 | 0.0838 | 0.0460 | 0.0299 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Xu, W.; Li, L.; Xu, X.; Qi, H.; Zhang, Z.; Yang, F.; Yan, Z.; Liu, C.; Yuan, R.; et al. Comparison on Quantitative Analysis of Olivine Using MarSCoDe Laser-Induced Breakdown Spectroscopy in a Simulated Martian Atmosphere. Remote Sens. 2022, 14, 5612. https://doi.org/10.3390/rs14215612
Liu X, Xu W, Li L, Xu X, Qi H, Zhang Z, Yang F, Yan Z, Liu C, Yuan R, et al. Comparison on Quantitative Analysis of Olivine Using MarSCoDe Laser-Induced Breakdown Spectroscopy in a Simulated Martian Atmosphere. Remote Sensing. 2022; 14(21):5612. https://doi.org/10.3390/rs14215612
Chicago/Turabian StyleLiu, Xiangfeng, Weiming Xu, Luning Li, Xuesen Xu, Hai Qi, Zhenqiang Zhang, Fan Yang, Zhixin Yan, Chongfei Liu, Rujun Yuan, and et al. 2022. "Comparison on Quantitative Analysis of Olivine Using MarSCoDe Laser-Induced Breakdown Spectroscopy in a Simulated Martian Atmosphere" Remote Sensing 14, no. 21: 5612. https://doi.org/10.3390/rs14215612
APA StyleLiu, X., Xu, W., Li, L., Xu, X., Qi, H., Zhang, Z., Yang, F., Yan, Z., Liu, C., Yuan, R., Wan, X., & Shu, R. (2022). Comparison on Quantitative Analysis of Olivine Using MarSCoDe Laser-Induced Breakdown Spectroscopy in a Simulated Martian Atmosphere. Remote Sensing, 14(21), 5612. https://doi.org/10.3390/rs14215612