Accessible Remote Sensing Data Mining Based Dew Estimation
Abstract
:1. Introduction
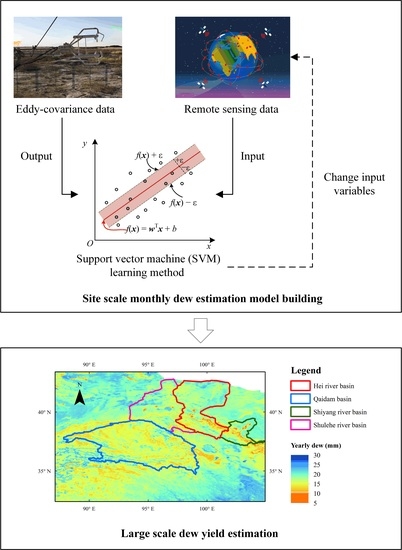
2. Materials and Methods
2.1. Study Area
2.2. Data Source
2.2.1. Eddy-Covariance Data
2.2.2. Remote Sensing Data
2.3. Methodology
2.3.1. Model Structure
2.3.2. Parametric Optimization Strategy
2.3.3. Contribution of Variables
2.3.4. Evaluation Criteria
3. Results
3.1. Variable Selection and Contributions
3.2. Model Performance at Site-Scale
3.3. Watershed-Scale Simulation
4. Discussion
4.1. Variable Screening for Dew Simulation
4.2. Distribution Characteristics of Dew in the HRB
4.3. Contribution of Dew to Water Balance
4.4. Model Applications in Northwest China
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Agam, N.; Berliner, P.R. Dew formation and water vapor adsorption in semi-arid environments—A review. J. Arid. Environ. 2006, 65, 572–590. [Google Scholar] [CrossRef]
- Wallin, J.R. Agrometeorological aspects of dew. Agric. Meteorol. 1967, 4, 85–102. [Google Scholar] [CrossRef]
- Nikolayev, V.S.; Beysens, D.; Gioda, A.; Milimouk, I.; Katiushin, E.; Morel, J.P. Water recovery from dew. J. Hydrol. 1996, 182, 19–35. [Google Scholar] [CrossRef] [Green Version]
- McHugh, T.A.; Morrissey, E.M.; Reed, S.C.; Hungate, B.A.; Schwartz, E. Water from air: An overlooked source of moisture in arid and semiarid regions. Sci. Rep. 2015, 5, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.X.; Kaseke, K.F.; Ravi, S.; Jiao, W.Z.; Mushi, R.; Shuuya, T.; Maggs-Kolling, G. Convergent vegetation fog and dew water use in the Namib Desert. Ecohydrology 2019, 12, 11. [Google Scholar] [CrossRef]
- Kidron, G.J.; Herrnstadt, I.; Barzilay, E. The role of dew as a moisture source for sand microbiotic crusts in the Negev Desert, Israel. J. Arid. Environ. 2002, 52, 517–533. [Google Scholar] [CrossRef]
- Guadarrama-Cetina, J.; Mongruel, A.; Medici, M.G.; Baquero, E.; Parker, A.R.; Milimouk-Melnytchuk, I.; Gonzalez-Vinas, W.; Beysens, D. Dew condensation on desert beetle skin. Eur. Phys. J. E 2014, 37, 6. [Google Scholar] [CrossRef]
- Malek, E.; McCurdy, G.; Giles, B. Dew contribution to the annual water balances in semi-arid desert valleys. J. Arid. Environ. 1999, 42, 71–80. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Suo, Y. A new water balance equation introducing dew amount in arid area. J. Hydraul. Eng. 2019, 50, 710–720. [Google Scholar]
- Liu, X.Y.; Xu, J.Z.; Yang, S.H.; Zhang, J.G.; Wang, Y.J. Vapor Condensation in Rice Fields and Its Contribution to Crop Evapotranspiration in the Subtropical Monsoon Climate of China. J. Hydrometeorol. 2018, 19, 1043–1057. [Google Scholar] [CrossRef]
- Beysens, D. Estimating dew yield worldwide from a few meteo data. Atmos. Res. 2016, 167, 146–155. [Google Scholar] [CrossRef]
- Nilsson, T.M.J.; Vargas, W.E.; Niklasson, G.A.; Granqvist, C.G. Condensation of water by radiative cooling. Renew. Energy 1994, 5, 310–317. [Google Scholar] [CrossRef]
- Jacobs, A.F.G.; Heusinkveld, B.G.; Berkowicz, S.M. Passive dew collection in a grassland area, The Netherlands. Atmos. Res. 2008, 87, 377–385. [Google Scholar] [CrossRef]
- Heusinkveld, B.G.; Berkowicz, S.M.; Jacobs, A.F.G.; Holtslag, A.A.M.; Hillen, W. An automated microlysimeter to study dew formation and evaporation in arid and semiarid regions. J. Hydrometeorol. 2006, 7, 825–832. [Google Scholar] [CrossRef] [Green Version]
- Hiltner, E. Der Tau und seine Bedeutung für den Pflanzenbau. Wiss. Arch. Landw. 1930, 3, 1–70. [Google Scholar]
- Kidron, G.J. A simple weighing method for dew and fog measurements. Weather 1998, 53, 428–433. [Google Scholar] [CrossRef]
- Beysens, D.; Milimouk, I.; Nikolayev, V.; Muselli, M.; Marcillat, J. Using radiative cooling to condense atmospheric vapor: A study to improve water yield. J. Hydrol. 2003, 276, 1–11. [Google Scholar] [CrossRef]
- Kidron, G.J.; Kronenfeld, R. Microlysimeters overestimate the amount of non-rainfall water—An experimental approach. Catena 2020, 194, 104691. [Google Scholar] [CrossRef]
- Madeira, A.C.; Kim, K.S.; Taylor, S.E.; Gleason, M.L. A simple cloud-based energy balance model to estimate dew. Agric. For. Meteorol. 2002, 111, 55–63. [Google Scholar] [CrossRef]
- Groh, J.; Slawitsch, V.; Herndl, M.; Graf, A.; Vereecken, H.; Putz, T. Determining dew and hoar frost formation for a low mountain range and alpine grassland site by weighable lysimeter. J. Hydrol. 2018, 563, 372–381. [Google Scholar] [CrossRef]
- Hao, X.M.; Li, C.; Guo, B.; Ma, J.X.; Ayup, M.; Chen, Z.S. Dew formation and its long-term trend in a desert riparian forest ecosystem on the eastern edge of the Taklimakan Desert in China. J. Hydrol. 2012, 472, 90–98. [Google Scholar] [CrossRef]
- Guo, X.; Zha, T.; Jia, X.; Wu, B.; Feng, W.; Xie, J.; Gong, J.; Zhang, Y.; Peltola, H. Dynamics of dew in a cold desert-shrub ecosystem and its abiotic controls. Atmosphere 2016, 7, 32. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem–Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Moro, M.J.; Were, A.; Villagarcia, L.; Canton, Y.; Domingo, F. Dew measurement by Eddy covariance and wetness sensor in a semiarid ecosystem of SE Spain. J. Hydrol. 2007, 335, 295–302. [Google Scholar] [CrossRef]
- Zhang, Z.; Gong, Y.; Wang, Z. Accessible remote sensing data based reference evapotranspiration estimation modelling. Agric. Water Manag. 2018, 210, 59–69. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gao, X.G.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Cosh, M.H.; Kabela, E.D.; Hornbuckle, B.; Gleason, M.L.; Jackson, T.J.; Prueger, J.H. Observations of dew amount using in situ and satellite measurements in an agricultural landscape. Agric. For. Meteorol. 2009, 149, 1082–1086. [Google Scholar] [CrossRef]
- Vuollekoski, H.; Vogt, M.; Sinclair, V.A.; Duplissy, J.; Jarvinen, H.; Kyro, E.M.; Makkonen, R.; Petaja, T.; Prisle, N.L.; Raisanen, P.; et al. Estimates of global dew collection potential on artificial surfaces. Hydrol. Earth Syst. Sci. 2015, 19, 601–613. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.P. A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Singer, Y.; Srebro, N.; Cotter, A. Pegasos: Primal estimated sub-gradient solver for SVM. Math. Program. 2011, 127, 3–30. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A Library for Support Vector Machines. Acm Trans. Intell. Syst. Technol. 2011, 2, 3. [Google Scholar] [CrossRef]
- Qiu, L.H.; Peng, D.Z.; Xu, Z.X.; Liu, W.F. Identification of the impacts of climate changes and human activities on runoff in the upper and middle reaches of the Heihe River basin, China. J. Water Clim. Chang. 2016, 7, 251–262. [Google Scholar] [CrossRef]
- Song, L.S.; Liu, S.M.; Kustas, W.P.; Nieto, H.; Sun, L.; Xu, Z.W.; Skaggs, T.H.; Yang, Y.; Ma, M.G.; Xu, T.R.; et al. Monitoring and validating spatially and temporally continuous daily evaporation and transpiration at river basin scale. Remote Sens. Environ. 2018, 219, 72–88. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Ma, M.; Xiao, Q.; Liu, Q.; Jin, R.; Che, T.; Wang, W.; Qi, Y.; Li, H.; et al. HiWATER:An Integrated Remote Sensing Experiment on Hydrological and Ecological Processes in the Heihe River Basin. Adv. Earth Sci. 2012, 27, 481–498. [Google Scholar]
- Liu, S.M.; Li, X.; Xu, Z.W.; Che, T.; Xiao, Q.; Ma, M.G.; Liu, Q.H.; Jin, R.; Guo, J.W.; Wang, L.X.; et al. The Heihe Integrated Observatory Network: A Basin-Scale Land Surface Processes Observatory in China. Vadose Zone J. 2018, 17, 21. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. Atmos. 2013, 118, 13–140. [Google Scholar] [CrossRef]
- Fang, J. Variability in condensation water and its determinants in arid regions of north-western China. Ecohydrology 2020, 13, e2226. [Google Scholar] [CrossRef]
- Meng, Y.; Wen, X.F. Characteristics of dew events in an arid artificial oasis cropland and a sub-humid cropland in China. J. Arid Land 2016, 8, 399–408. [Google Scholar] [CrossRef] [Green Version]
- De Jeu, R.; Heusinkveld, B.; Vugts, H.; Holmes, T.; Owe, M. Remote sensing techniques to measure dew: The detection of canopy water with an L-band passive microwave radiometer and a spectral reflectance sensor. In Proceedings of the Conference on Remote Sensing for Agriculture, Ecosystems and Hydrology VI, Maspalomas, Spain, 14–16 September 2004; pp. 225–235. [Google Scholar]
- Zhuang, Y.; Zhao, W. Dew formation and its variation in Haloxylon ammodendron plantations at the edge of a desert oasis, northwestern China. Agric. For. Meteorol. 2017, 247, 541–550. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Gevrey, M.; Dimopoulos, I.; Lek, S. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecol. Model. 2003, 160, 249–264. [Google Scholar] [CrossRef]
- Olden, J.D.; Jackson, D.A. Illuminating the “black box”: A randomization approach for understanding variable contributions in artificial neural networks. Ecol. Model. 2002, 154, 135–150. [Google Scholar] [CrossRef]
- Garson, G.D. Interpreting neural-network connection strengths. AI Expert 1991, 6, 47–51. [Google Scholar]
- MATLAB and Deep Learning Toolbox, R2021b; The MathWorks, Inc.: Natick, MA, USA, 2021.
- Beysens, D.; Mongruel, A.; Acker, K. Urban dew and rain in Paris, France: Occurrence and physico-chemical characteristics. Atmos. Res. 2017, 189, 152–161. [Google Scholar] [CrossRef] [Green Version]
- Tuure, J.; Korpela, A.; Hautala, M.; Hakojärvi, M.; Mikkola, H.; Räsänen, M.; Duplissy, J.; Pellikka, P.; Petäjä, T.; Kulmala, M.; et al. Comparison of surface foil materials and dew collectors location in an arid area: A one-year field experiment in Kenya. Agric. For. Meteorol. 2019, 276–277, 107613. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Multiple Linear Regression Models with Limited Data for the Prediction of Reference Evapotranspiration of the Peloponnese, Greece. Hydrology 2022, 9, 124. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F.; Fernandes, E.I. Exploring machine learning and multi-task learning to estimate meteorological data and reference evapotranspiration across Brazil. Agric. Water Manag. 2022, 259, 107281. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Artificial Neural Networks for the Prediction of the Reference Evapotranspiration of the Peloponnese Peninsula, Greece. Water 2022, 14, 2027. [Google Scholar] [CrossRef]
- Zakeri, M.S.; Mousavi, S.F.; Farzin, S.; Sanikhani, H. Modeling of Reference Crop Evapotranspiration in Wet and Dry Climates Using Data-Mining Methods and Empirical Equations. J. Soft Comput. Civ. Eng. 2022, 6, 1–28. [Google Scholar] [CrossRef]
- Pan, Y.X.; Wang, X.P.; Zhang, Y.F.; Hu, R. Dew formation characteristics at annual and daily scale in xerophyte shrub plantations at Southeast margin of Tengger desert, Northern China. Ecohydrology 2018, 11, 13. [Google Scholar] [CrossRef]
- Pan, Y.X.; Wang, X.P.; Zhang, Y.F. Dew formation characteristics in a revegetation-stabilized desert ecosystem in Shapotou area, Northern China. J. Hydrol. 2010, 387, 265–272. [Google Scholar] [CrossRef]
- Pinter, P.J. Effect of dew on canopy reflectance and temperature. Remote Sens. Environ. 1986, 19, 187–205. [Google Scholar] [CrossRef]
- Lin, B.; Minnis, P. Temporal variations of land surface microwave emissivities over the atmospheric radiation measurement program southern great plains site. J. Appl. Meteorol. 2000, 39, 1103–1116. [Google Scholar] [CrossRef]
- Jia, Z.; Zhao, Z.; Zhang, Q.; Wu, W. Dew yield and its influencing factors at the western edge of Gurbantunggut desert, China. Water 2019, 11, 733. [Google Scholar] [CrossRef] [Green Version]
- Aguirre-Gutiérrez, C.A.; Holwerda, F.; Goldsmith, G.R.; Delgado, J.; Yepez, E.; Carbajal, N.; Escoto-Rodríguez, M.; Arredondo, J.T. The importance of dew in the water balance of a continental semiarid grassland. J. Arid. Environ. 2019, 168, 26–35. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, S.; Wang, S.S.; Zhao, Y.D.; Wen, X.M. Influence factors and variation characteristics of water vapor absorption by soil in semi-arid region. Sci China Earth Sci 2016, 59, 2240–2251. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, C.; Wang, Y.; Ma, Z. Spatiotemporal variations of precipitation in China using surface gauge observations from 1961 to 2016. Atmosphere 2020, 11, 303. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.W.; Liu, S.M.; Zhu, Z.L.; Zhou, J.; Shi, W.J.; Xu, T.R.; Yang, X.F.; Zhang, Y.; He, X.L. Exploring evapotranspiration changes in a typical endorheic basin through the integrated observatory network. Agric. For. Meteorol. 2020, 290, 108010. [Google Scholar] [CrossRef]
- Feng, J.; Wang, Z. A satellite-based energy balance algorithm with reference dry and wet limits. Int. J. Remote Sens. 2013, 34, 2925–2946. [Google Scholar] [CrossRef]
- Yang, T.; Ala, M.; Guan, D.; Wang, A. The Effects of Groundwater Depth on the Soil Evaporation in Horqin Sandy Land, China. Chin. Geogr. Sci. 2021, 31, 727–734. [Google Scholar] [CrossRef]















| Station | Lon | Lat | Elevation (m) | Observation Period | Landscapes |
|---|---|---|---|---|---|
| AR | 100.4643 | 38.0473 | 3033 | January 2013–December 2017 | Alpine grassland |
| HYL | 101.1236 | 41.9928 | 876 | January 2014–December 2015 | P. euphratica |
| YK | 100.2421 | 38.0142 | 4148 | September 2015–December 2017 | Alpine tundra |
| LD | 101.1326 | 41.9993 | 878 | January 2014–December 2015 | Barren-land |
| HZZ | 100.3201 | 38.7659 | 1731 | June 2015–December 2017 | Desert |
| SSW | 100.4933 | 38.7892 | 1594 | January 2013–April 2015 | Desert |
| BJT | 100.3042 | 38.9150 | 1562 | January 2013–December 2014 | Desert |
| HM | 100.9872 | 42.1135 | 1054 | May 2015–December 2017 | Desert |
| DM | 100.3722 | 38.8555 | 1556 | January 2013–December 2017 | Maize |
| Variable Name | Description | Units |
|---|---|---|
| NDVI | Normalized Difference Vegetation Index | / |
| LSTD | Daytime Land Surface Temperature | Kelvin |
| LSTN | Nighttime Land Surface Temperature | Kelvin |
| Emis20 | Band 20 (3.660–3.840 µm) emissivity | / |
| Emis22 | Band 22 (3.929–3.989 µm) emissivity | / |
| Emis23 | Band 23 (4.020–4.080 µm) emissivity | / |
| Emis29 | Band 29 (8.400–8.700 µm) emissivity | / |
| Emis31 | Band 31 (10.780–11.280 µm) emissivity | / |
| Emis32 | Band 32 (11.770–12.270 µm) emissivity | / |
| Model No. | Variables | Training Set | Test Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CC | NMB | SD | RMSE | adj.R2 | CC | NMB | SD | RMSE | adj.R2 | ||
| m31 | LSTD, LSTN; Emis31 | 0.73 | 6.57 | 0.30 | 0.49 | 0.44 | 0.57 | 6.27 | 0.28 | 0.55 | 0.23 |
| m32 | LSTD, LSTN; Emis32 | 0.66 | 5.25 | 0.47 | 0.50 | 0.42 | 0.54 | 6.53 | 0.45 | 0.56 | 0.20 |
| m33 | LSTD, LSTN; Emis23 | 0.62 | 7.50 | 0.40 | 0.52 | 0.35 | 0.51 | 8.10 | 0.40 | 0.58 | 0.16 |
| m41 | LSTD, LSTN; Emis23, Emis31 | 0.76 | 4.42 | 0.49 | 0.43 | 0.57 | 0.57 | 3.95 | 0.48 | 0.55 | 0.23 |
| m42 | LSTD, LSTN; NDVI, Emis22 | 0.74 | 4.28 | 0.46 | 0.44 | 0.53 | 0.56 | 5.16 | 0.44 | 0.55 | 0.22 |
| m43 | LSTD, LSTN; NDVI, Emis23 | 0.79 | 4.89 | 0.48 | 0.41 | 0.60 | 0.55 | 5.75 | 0.46 | 0.57 | 0.15 |
| m51 | LSTD, LSTN; NDVI, Emis29, Emis31 | 0.79 | 3.95 | 0.50 | 0.41 | 0.61 | 0.62 | 1.08 | 0.52 | 0.52 | 0.29 |
| m52 | LSTD, LSTN; NDVI, Emis29, Emis32 | 0.75 | 4.74 | 0.48 | 0.44 | 0.54 | 0.59 | 4.17 | 0.50 | 0.55 | 0.26 |
| m53 | LSTD, LSTN; Emis23, Emis29, Emis31 | 0.81 | 3.20 | 0.51 | 0.39 | 0.65 | 0.55 | 3.00 | 0.52 | 0.57 | 0.16 |
| m61 | LSTD, LSTN; NDVI, Emis22, Emis29, Emis31 | 0.88 | 3.21 | 0.53 | 0.30 | 0.77 | 0.64 | 10.60 | 0.59 | 0.61 | 0.28 |
| m62 | LSTD, LSTN; NDVI, Emis22, Emis31, Emis32 | 0.89 | 2.00 | 0.56 | 0.30 | 0.78 | 0.59 | −2.44 | 0.52 | 0.55 | 0.23 |
| m63 | LSTD, LSTN; NDVI, Emis20, Emis23, Emis31 | 0.85 | 3.77 | 0.53 | 0.35 | 0.71 | 0.59 | 3.51 | 0.50 | 0.55 | 0.21 |
| m71 | LSTD, LSTN; NDVI, Emis20, Emis22, Emis29, Emis31 | 0.91 | 2.07 | 0.56 | 0.27 | 0.82 | 0.64 | 7.61 | 0.56 | 0.55 | 0.25 |
| m72 | LSTD, LSTN; NDVI, Emis20, Emis23, Emis31, Emis32 | 0.87 | 0.70 | 0.53 | 0.33 | 0.74 | 0.62 | 1.99 | 0.61 | 0.56 | 0.21 |
| m73 | LSTD, LSTN; NDVI, Emis20, Emis23, Emis29, Emis31 | 0.73 | 5.47 | 0.52 | 0.46 | 0.50 | 0.57 | 3.74 | 0.52 | 0.56 | 0.17 |
| m81 | LSTD, LSTN; NDVI, Emis20, Emis22, Emis23, Emis29, Emis31 | 0.80 | 4.50 | 0.51 | 0.39 | 0.62 | 0.61 | 5.15 | 0.50 | 0.53 | 0.23 |
| m82 | LSTD, LSTN; NDVI, Emis22, Emis23, Emis29, Emis31, Emis32 | 0.73 | 5.54 | 0.49 | 0.45 | 0.51 | 0.59 | 3.83 | 0.50 | 0.56 | 0.13 |
| m83 | LSTD, LSTN; NDVI, Emis20, Emis22, Emis23, Emis31, Emis32 | 0.76 | 5.00 | 0.50 | 0.43 | 0.56 | 0.55 | 4.18 | 0.49 | 0.57 | 0.11 |
| m91 | ALL | 0.67 | 7.40 | 0.42 | 0.50 | 0.41 | 0.60 | 7.46 | 0.42 | 0.53 | 0.21 |
| m92 | ALL | 0.67 | 7.14 | 0.42 | 0.49 | 0.41 | 0.59 | 7.39 | 0.41 | 0.53 | 0.20 |
| m93 | ALL | 0.67 | 7.39 | 0.42 | 0.49 | 0.41 | 0.60 | 6.68 | 0.41 | 0.54 | 0.18 |
| Emis31 | Emis23 | Emis29 | LSTN | NDVI | Emis22 | LSTD | Emis32 | Emis20 | |
|---|---|---|---|---|---|---|---|---|---|
| Relative contribution | 17.54% | 11.88% | 11.73% | 11.37% | 11.29% | 10.94% | 9.46% | 9.36% | 6.42% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suo, Y.; Wang, Z.; Zhang, Z.; Fassnacht, S.R. Accessible Remote Sensing Data Mining Based Dew Estimation. Remote Sens. 2022, 14, 5653. https://doi.org/10.3390/rs14225653
Suo Y, Wang Z, Zhang Z, Fassnacht SR. Accessible Remote Sensing Data Mining Based Dew Estimation. Remote Sensing. 2022; 14(22):5653. https://doi.org/10.3390/rs14225653
Chicago/Turabian StyleSuo, Ying, Zhongjing Wang, Zixiong Zhang, and Steven R. Fassnacht. 2022. "Accessible Remote Sensing Data Mining Based Dew Estimation" Remote Sensing 14, no. 22: 5653. https://doi.org/10.3390/rs14225653
APA StyleSuo, Y., Wang, Z., Zhang, Z., & Fassnacht, S. R. (2022). Accessible Remote Sensing Data Mining Based Dew Estimation. Remote Sensing, 14(22), 5653. https://doi.org/10.3390/rs14225653