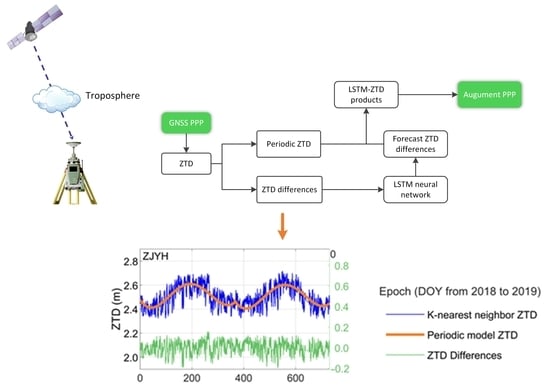
A Tropospheric Zenith Delay Forecasting Model Based on a Long Short-Term Memory Neural Network and Its Impact on Precise Point Positioning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Preprocessing
2.1.1. Outlier Elimination
2.1.2. Data Gap Interpolation
2.1.3. GNSS ZTD Testing Accuracy Validation
2.2. LSTM-ZTD Model Construction
2.2.1. ZTD Differences Extraction
2.2.2. LSTM-ZTD Model Construction
3. Results and Analysis
3.1. Validation from ZTD Models Perspective
3.2. Validation from PPP Perspective
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ZTD | Zenith tropospheric delay |
| ZHD | Zenith hydrostatic delay |
| ZWD | Zenith wet delay |
| GNSS | Global navigation satellite system |
| PPP | Precise point position |
| RTK | Real-Time Kinematic positioning |
| NGCC | The National Geomatics Center of China |
| LSTM | Long short-term memory |
| ECMWF | The European Centre for Medium-Range Weather Forecasts |
| BPNN | Back Propagation Neural Network |
| RMSE | Root-mean-square error |
| STD | Standard deviation |
| IGS | International GNSS service |
| RTS | Real-time service |
| EGNOS | European Geostationary Navigation Overlay Service |
| UNB | University of New Brunswick model |
| GPT | The global temperature and pressure |
| ICA | Independent component analysis |
| PCA | Principal component analysis |
| DOY | Day of year |
| HOD | Hour of day |
| RAM | Random access memory |
| L-PPP | LSTM-ZTD constrained PPP |
| C-PPP | Conventional ionospheric-free combined PPP |
| T | Accumulated DOY from 2018 to 2019 |
References
- Blewitt, G. Carrier phase ambiguity resolution for the Global Positioning System applied to geodetic baselines up to 2000 km. J. Geophys. Res. Solid Earth 1989, 94, 10187–10203. [Google Scholar] [CrossRef] [Green Version]
- Malys, S.; Jensen, P.A. Geodetic Point Positioning with GPS Carrier Beat Phase Data from the CASA UNO Experiment. Geophys. Res. Lett. 1990, 17, 651–654. [Google Scholar] [CrossRef]
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Kouba, J. Implementation and testing of the gridded Vienna Mapping Function 1 (VMF1). J. Geod. 2008, 82, 193–205. [Google Scholar] [CrossRef]
- Tao, Y.; Liu, C.; Liu, C.; Zhao, X.; Hu, H. Empirical Wavelet Transform Method for GNSS Coordinate Series Denoising. J. Geovis. Spatial Anal. 2021, 5, 9. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Kos, T.; Botincan, M.; Markezic, I. Estimation of tropospheric delay models compliance. In Proceedings of the 2008 50th International Symposium ELMAR, Borik Zadar, Croatia, 10–12 September 2022; IEEE: Piscataway, NJ, USA, 2008; Volume 2, pp. 381–384. [Google Scholar]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géodésique 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Black, H.D. An easily implemented algorithm for the tropospheric range correction. J. Geophys. Res. Solid Earth 1978, 83, 1825–1828. [Google Scholar] [CrossRef]
- Hopfield, H. Two-quartic tropospheric refractivity profile for correcting satellite data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Penna, N.; Dodson, A.; Chen, W. Assessment of EGNOS tropospheric correction model. J. Navig. 2001, 54, 37–55. [Google Scholar] [CrossRef]
- Collins, J.P.; Langley, R.B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System; Department of Geodesy and Geomatics Engineering, University of New Brunswick: Fredericton, NB, Canada, 1997. [Google Scholar]
- Leandro, R.; Santos, M.; Langley, R. “UNB Neutral Atmosphere Models: Development and Performance”. In Proceedings of the 2006 National Technical Meeting of The Institute of Navigation, Monterey, CA, USA, 18–20 January 2006; pp. 564–573. [Google Scholar]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Bock, O.; Willis, P.; Wang, J.; Mears, C. A high-quality, homogenized, global, long-term (1993–2008) DORIS precipitable water data set for climate monitoring and model verification. J. Geophys. Res. Atmos. 2014, 119, 7209–7230. [Google Scholar] [CrossRef]
- Alshawaf, F.; Zus, F.; Balidakis, K.; Deng, Z.; Hoseini, M.; Dick, G.; Wickert, J. On the statistical significance of climatic trends estimated from GPS tropospheric time series. J. Geophys. Res. Atmos. 2018, 123, 10–967. [Google Scholar] [CrossRef] [Green Version]
- De Haan, S. Assimilation of GNSS ZTD and radar radial velocity for the benefit of very short-range regional weather forecasts. Q. J. R. Meteorol. Soc. 2013, 139, 2097–2107. [Google Scholar] [CrossRef]
- Nowel, K. Specification of deformation congruence models using combinatorial iterative DIA testing procedure. J. Geod. 2020, 94, 1–23. [Google Scholar] [CrossRef]
- Yang, L.; Shen, Y.; Li, B.; Rizos, C. Simplified algebraic estimation for the quality control of DIA estimator. J. Geod. 2021, 95, 1–15. [Google Scholar] [CrossRef]
- Hadas, T.; Kaplon, J.; Bosy, J.; Sierny, J.; Wilgan, K. Near-real-time regional troposphere models for the GNSS precise point positioning technique. Meas. Sci. Technol. 2013, 24, 055003. [Google Scholar] [CrossRef]
- Shi, J.; Xu, C.; Guo, J.; Gao, Y. Local troposphere augmentation for real-time precise point positioning. Earth Planets Space 2014, 66, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Peng, W.; Xu, C.; Cheng, S. Enhancing real-time precise point positioning with zenith troposphere delay products and the determination of corresponding tropospheric stochastic models. Geophys. Suppl. Mon. Not. R. Astron. Soc. 2016, 208, 1217–1230. [Google Scholar] [CrossRef]
- De Oliveira, P.; Morel, L.; Fund, F.; Legros, R.; Monico, J.; Durand, S.; Durand, F. Modeling tropospheric wet delays with dense and sparse network configurations for PPP-RTK. GPS Solut. 2017, 21, 237–250. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W. Real-time wide-area precise tropospheric corrections (WAPTCs) jointly using GNSS and NWP forecasts for China. J. Geod. 2022, 96, 1–18. [Google Scholar] [CrossRef]
- Chen, W.; Gao, C.; Pan, S. Assessment of GPT2 empirical troposphere model and application analysis in precise point positioning. In Proceedings of the China Satellite Navigation Conference (CSNC) 2014 Proceedings, Berlin, Germany, 26 April 2014; Volume II. [Google Scholar]
- Song, C.; Hao, J.; Zhang, H. A Method to Accelerate PPP Re-Convergence with Prior Troposphere Delay Constraint. J. Geom. Sci. Technol. 2015, 32, 441–444. [Google Scholar]
- Jia, S.; Min, L.; Qile, Z.; Zhiqiang, D. A Real Time Regional Zenith Troposphere Delay Model and Its Application in PPP. Bull. Surv. Mapp. 2018, 4, 1. [Google Scholar]
- Nikolaidou, T.; Nievinski, F.; Balidakis, K.; Schuh, H.; Santos, M. PPP without troposphere estimation: Impact assessment of regional versus global numerical weather models and delay parametrization. In Proceedings of the International Symposium on Advancing Geodesy in a Changing World, Kobe, Japan, 30 July–4 August 2018; Springer: Cham, Germany, 2018; pp. 107–118. [Google Scholar]
- Pikridas, C.; Katsougiannopoulos, S.; Ifadis, I. Predicting Zenith Tropospheric Delay using the Artificial Neural Network technique. Application to selected EPN stations. J. Nat. Cancer Inst. 2010, 88, 1803–1805. [Google Scholar]
- Wang, Y.; Zhang, L.; Yang, J. Prediction of zenith tropospheric delay based on BP neural network. In Advances in Computer Science and Education; Springer: Berlin/Heidelberg, Germany, 2012; pp. 459–465. [Google Scholar]
- Zhang, Q.; Li, F.; Zhang, S.; Li, W. Modeling and forecasting the GPS zenith troposphere delay in West Antarctica based on different blind source separation methods and deep learning. Sensors 2020, 20, 2343. [Google Scholar] [CrossRef] [Green Version]
- Ding, M.; Hu, W.; Jin, X.; Yu, L. A new ZTD model based on permanent ground-based GNSS-ZTD data. Surv. Rev. 2015, 48, 385–391. [Google Scholar] [CrossRef]
- Xiao, G.; Ou, J.; Liu, G.; Zhang, H. Construction of a regional precise tropospheric delay model based on improved BP neural network. Chin. J. Geophys. 2018, 61, 3139–3148. [Google Scholar]
- Yang, Y.; Xu, T.; Ren, L. A new regional tropospheric delay correction model based on BP neural network. In Proceedings of the 2017 Forum on Cooperative Positioning and Service (CPGPS), Harbin, China, 19–21 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 96–100. [Google Scholar]
- Zheng, D.; Hu, W.; Wang, J.; Zhu, M. Research on regional zenith tropospheric delay based on neural network technology. Surv. Rev. 2015, 47, 286–295. [Google Scholar] [CrossRef]
- Yao, Y.; Xu, X.; Xu, C.; Peng, W.; Wan, Y. GGOS tropospheric delay forecast product performance evaluation and its application in real-time PPP. J. Atmosph. Solar-Terr. Phys. 2018, 175, 1–17. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Chen, K. Performance analysis of precise point positioning using real-time orbit and clock products. J. Glob. Position. Syst. 2004, 3, 95–100. [Google Scholar] [CrossRef]
- Baarda, W. Statistical Concepts in Geodesy; Netherlands Geodetic Commission: Amersfoort, The Netherlands, 1967; Volume 2, pp. 1–74. [Google Scholar]
- Li, B.; Zhao, K.; Sandoval, E.B. A UWB-Based Indoor Positioning System Employing Neural Networks. J. Geovis. Spat. Anal. 2020, 4, 18. [Google Scholar] [CrossRef]
- Baarda, W. A Testing Procedure for Use in Geodetic Networks; Netherlands Geodetic Commission: Amersfoort, The Netherlands, 1968; Volume 2, pp. 1–97. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Duchesnay, E. Scikit-learn: Machine Learning in Python. JMLR 2011, 12, 2825–2830. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.L.; Chen, L. A nonlinear hybrid wind speed forecasting model using LSTM network, hysteretic ELM and Differential Evolution algorithm. Energy Convers. Manag. 2018, 173, 123–142. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Huang, B.; Ji, Z.; Zhai, R.; Xiao, C.; Yang, F.; Yang, B.; Wang, Y. Clock bias prediction algorithm for navigation satellites based on a supervised learning long short-term memory neural network. GPS Solut. 2021, 25, 1–16. [Google Scholar] [CrossRef]
- Liu, L.; Zou, S.; Yao, Y.; Wang, Z. Forecasting global ionospheric TEC using deep learning approach. Space Weather 2020, 18, e2020SW002501. [Google Scholar] [CrossRef]
- Mendez Astudillo, J.; Lau, L.; Tang, Y.T.; Moore, T. Analysing the zenith tropospheric delay estimates in on-line precise point positioning (PPP) services and PPP software packages. Sensors 2018, 18, 580. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Yao, Y.; Xu, C.; Xu, W.; Shi, J. Transformer-Based Global Zenith Tropospheric Delay Forecasting Model. Remote Sens. 2022, 14, 3335. [Google Scholar] [CrossRef]
- Wilgan, K.; Hurter, F.; Geiger, A.; Rohm, W.; Bosy, J. Tropospheric refractivity and zenith path delays from least-squares collocation of meteorological and GNSS data. J. Geod. 2017, 91, 117–134. [Google Scholar] [CrossRef] [Green Version]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. Solid Earth 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Vaclavovic, P.; Dousa, J.; Elias, M.; Kostelecky, J. Using external tropospheric corrections to improve GNSS positioning of hot-air balloon. GPS Solut. 2017, 21, 1479–1489. [Google Scholar] [CrossRef]










| Items | Strategies |
|---|---|
| Observations | GPS/GLONASS raw pseudo range and phase observables |
| Frequency selection | L1 & L2 |
| Orbit and clock | IGS final products |
| Sampling rate | 30 s |
| Combination mode | IF combinations |
| Ambiguity Fixed | Float solutions (random walk process 10−4 mm/) |
| Weight for observations | Elevation-dependent weight |
| Phase windup effect | Corrected |
| Station coordinates | Fixed |
| Station displacement | Solid Earth tides, ocean tides, and pole tide displacements |
| Satellite/receiver PCO/PCV | IGS14_2156.atx |
| DCB | CODE P1-C1 |
| Elevation angle | 7° |
| Sampling rate | 30 s |
| ZHD | Saastamoinen |
| Mapping function | NMF |
| Orbit and clock errors | GBM final orbit and clock |
| Parameter estimator | Kalman filter (smooth) |
| Model | Bias (cm) | STD (cm) | RMS (cm) | R | MAE (cm) |
|---|---|---|---|---|---|
| Periodic model ZTD | 2.99 | 1.96 | 3.57 | 0.78 | 2.99 |
| KNN ZTD | 2.77 | 1.52 | 3.16 | 0.86 | 2.77 |
| GNSS Stations APPROX POSITION | VMF Grid | |||
|---|---|---|---|---|
| Stations | Lon (°) | Lat (°) | Lon (°) | Lat (°) |
| CQPS | 108.222 | 29.359 | 108.5 | 29.5 |
| GXCZ | 107.322 | 22.391 | 107.5 | 22.5 |
| JLHC | 131.104 | 43.223 | 131.5 | 43.5 |
| JSHZ | 118.913 | 33.307 | 118.5 | 33.5 |
| SXQY | 112.335 | 36.509 | 112.5 | 36.5 |
| SXYQ | 111.660 | 35.277 | 111.5 | 35.5 |
| ZJYH | 119.689 | 28.266 | 119.5 | 28.5 |
| Conventional PPP | GPT2-ZTD Corrected PPP | LSTM-ZTD Corrected PPP | |
|---|---|---|---|
| Troposphere ZWD | Estimation (Random walk process 10 mm/) | GPT2-ZTD and estimation (Random walk process 10 mm/) | LSTM-ZTD and estimation (Random walk process 10 mm/) |
| Initial ZTD | Saastamoinen | The first of GPT2-ZTD | The first of LSTM-ZTD |
| Stations | Summer (T 514) | Autumn (T 608) | Winter (T 693) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C-PPP | G-PPP | L-PPP | C-PPP | G-PPP | L-PPP | C-PPP | G-PPP | L-PPP | |
| JSHZ | 26 | 25.5 | 23.5 | 22.5 | 21 | 21 | 17 | 12 | 8 |
| SXQY | 23.5 | 23 | 21.5 | 15.5 | 12.5 | 12.5 | 10.5 | 10 | 9.5 |
| SXYQ | 24.5 | 25 | 22 | 15.5 | 15 | 14.5 | 20 | 16 | 10.5 |
| GXCZ | 26 | 24 | 18.5 | 16 | 12 | 9 | 17.5 | 15.5 | 13.5 |
| CQPS | 23.5 | 22 | 22.5 | 19.5 | 16 | 13.5 | 21.5 | 18.5 | 14 |
| JLHC | 26.5 | 21.5 | 21.5 | 20.5 | 18 | 14 | 22 | 21 | 16.5 |
| ZJYH | 16 | 17 | 13.5 | 14.5 | 12.5 | 11.5 | 18.5 | 16.5 | 16 |
| Average | 23.7 | 22.6 | 20.4 | 17.7 | 15.3 | 13.7 | 18.1 | 15.6 | 12.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yao, Y.; Hu, M.; Xu, C.; Su, X.; Che, D.; Peng, W. A Tropospheric Zenith Delay Forecasting Model Based on a Long Short-Term Memory Neural Network and Its Impact on Precise Point Positioning. Remote Sens. 2022, 14, 5921. https://doi.org/10.3390/rs14235921
Zhang H, Yao Y, Hu M, Xu C, Su X, Che D, Peng W. A Tropospheric Zenith Delay Forecasting Model Based on a Long Short-Term Memory Neural Network and Its Impact on Precise Point Positioning. Remote Sensing. 2022; 14(23):5921. https://doi.org/10.3390/rs14235921
Chicago/Turabian StyleZhang, Huan, Yibin Yao, Mingxian Hu, Chaoqian Xu, Xiaoning Su, Defu Che, and Wenjie Peng. 2022. "A Tropospheric Zenith Delay Forecasting Model Based on a Long Short-Term Memory Neural Network and Its Impact on Precise Point Positioning" Remote Sensing 14, no. 23: 5921. https://doi.org/10.3390/rs14235921
APA StyleZhang, H., Yao, Y., Hu, M., Xu, C., Su, X., Che, D., & Peng, W. (2022). A Tropospheric Zenith Delay Forecasting Model Based on a Long Short-Term Memory Neural Network and Its Impact on Precise Point Positioning. Remote Sensing, 14(23), 5921. https://doi.org/10.3390/rs14235921