A Hypered Deep-Learning-Based Model of Hyperspectral Images Generation and Classification for Imbalanced Data

Abstract

Recently, hyperspectral image (HSI) classification has become a hot topic in the geographical images research area. Sufficient samples are required for image classes to properly train classification models. However, a class imbalance problem has emerged in hyperspectral image (HSI) datasets as some classes do not have enough samples for training, and some classes have many samples. Therefore, the performance of classifiers is likely to be biased toward the classes with the largest samples, and this can lead to a decrease in the classification accuracy. Therefore, a new deep-learning-based model is proposed for hyperspectral images generation and classification of imbalanced data. Firstly, the spectral features are extracted by a 1D convolutional neural network, whereas a 2D convolutional neural network extracts the spatial features and the extracted spatial features and spectral features are catenated into a stacked spatial–spectral feature vector. Secondly, an autoencoder model was developed to generate synthetic images for minority classes, and the image samples were balanced. The GAN model is applied to determine the synthetic images from the real ones and then enhancing the classification performance. Finally, the balanced datasets are fed to a 2D CNN model for performing classification and validating the efficiency of the proposed model. Our model and the state-of-the-art classifiers are evaluated by four open-access HSI datasets. The results showed that the proposed approach can generate better quality samples for rebalancing datasets, which in turn noticeably enhances the classification performance compared to the existing classification models.

1. Introduction

Hyperspectral images (HSI) are characterized by high resolution, high dimension, and rich spatial and spectral information captured by various wavelengths with the spectrum in hundreds of adjacent bands [1]. The applications of HSIs are popularly used in numerous areas, such as sea ice detection, ecosystem monitoring, vegetation species analysis, and classification tasks [2,3].

Recently, HSI classification has become an interesting topic in research and industrial aspects [4,5]. However, the image classification task is complex [6]. HSI obtains huge number of wavebands which increases the challenge on classification models to obtain higher accuracy results, especially with the lack of training samples. Traditional methods depend on the experience of experts and the adjustment of hypermeters to manually design and extract main features. Machine learning approaches have been applied in image classification, including multiple logistic regression, Ada boost, support vector machines, etc. [7]. In addition, using deep-learning-based approaches can efficiently obtain highly robust and discriminative features in an automatic parameter tuning and data-driven manner [8]. They can provide more accurate classification results than other learning methods [9,10]. However, hyperspectral images suffer from class imbalance, and images have high dimensions and contain rich spectral information. Thus, research in hyperspectral image classification HSIC should consider the following challenges:

• Existing hyperspectral image datasets have an imbalanced-class issue. There are classes with insufficient samples for training, which makes the classification models biased toward the majority classes and influences the classification accuracy and results.
• Hyperspectral images have high dimensionality. Therefore, feature extraction is another challenging issue. How can we develop a strategy to capture the spatial features and spectral features effectively? Once spatial–spectral features are extracted well, the classification accuracy can be improved, and significant details about the structure of the locations can be obtained.
• During HSI classification, which deals with a huge number of images and their features, traditional models usually adopt a 3D conventional network to perform image classification. However, the 3D conventional-based classifier is a time-consuming method. There is a need to adopt a classifier that can efficiently perform classification tasks with less required time consumption.

Considering the class imbalance problem in HSI datasets, this article proposes a novel deep-learning-based model to provide a solution for the class imbalance issue for HSI classification. The proposed model applies a 1D_2D convolutional network for extracting the spatial–spectral features. Moreover, autoencoder and GAN networks are adopted for producing synthetic images of minority classes and then rebalancing the datasets. Finally, a 2D convolutional network is adopted for applying the image classification on the balanced datasets.

To sum up, this paper has the following contributions:

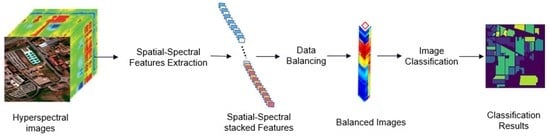
• Proposing an innovative 1D_2D convolutional-based method for obtaining the spatial and spectral features from hyperspectral images. A 1D CNN network is adopted to extract the spectral features, whereas a 2D convolutional network is used to capture the spatial features. Finally, the two features are concatenated and stacked into one feature vector.
• The autoencoder GAN-based model is proposed to solve the class imbalance issue, and synthetic images are generated to rebalance the minority classes and the datasets. Compared to the sample number in the majority class, an encoder cell would be determined and developed to produce samples for each minority class equal to the sample number in the majority class. The GAN model would be used to recognize the real samples and synthetic samples to enhance the results of the loss function, and improve the training convergence.
• We introduce a simpler and more efficient way of HSI classification. A 2D CNN-based classifier is adopted for classifying hyperspectral images. The 2D convolutional network costs less time consumption and takes less space for the training process. The balanced images, including the synthetic and the real images, are fed into the proposed classifier for performing the image classification task.
• Our model is validated using four hyperspectral datasets, including Salinas, Indian Pines, Botswana, and Kennedy Space Center. Our model is validated and compared with several state-of-the-art classifiers. Statistical significance is also estimated to examine classification performance obtained by the proposed model.

The remainder of this article is structured as following. In the next section, the related work is briefly reviewed. Section 3 describes our proposed model in detail. Experiment settings and information on datasets are illustrated in Section 4. The obtained results are presented in Section 5 and followed by the discussion in Section 6. Finally, the conclusions are summarized in Section 7.

2. Related Work

Many works in the literature address the class imbalance issue in HSI datasets. Here is a brief introduction to the research related to feature extraction, image generation, and classification for imbalanced data in HSI.

2.1. Feature Extraction Methods

The feature extraction process plays a vital role in HSI classification. A lot of methods have been proposed, and many approaches have been developed for enhancing classification performance. Convolutional neural networks have been considered for feature extraction approaches [11,12]. The automatic architecture of CNNs for the HSI classification was introduced in [13], which designed a 1D_3D Auto-CNN-based model to automatically obtain the features from the original image cube. The authors in [14] used a Gabor-filtering-based combination and a CNN-based model to obtain the spectral and spectral features, leading to a performance improvement. Zhang et al. [15] applied a 3D-based FractalNets method and the residual connections to extract the spatial–spectral features properly. Gao et al. [16] introduced a dual-branch-based feature extraction method along with an attention classification method for performing multiscale classification. The authors applied constructing multiple residual-like connections to assist in extracting the features at a granular level. Seydgar et al. [17] adopted ConvLSTM and 3D CNN methods to obtain the spatial–spectral features in HSI. Authors in [18,19] presented a 3D-CNN-based approach for HSI classification by applying 3D convolutional networks to properly obtain the spatial–spectral features.

Except for the CNN-based models, Vision-Transformer-related methods have become a new scheme for feature extraction in HSI. Dalal et al. [20] developed a transformation reduction (ETR) for reducing the dimensionality and classification complexity in HSI. Wang et al. [21] developed a Transformer network named UNetFormer for real-time urban scene segmentation and image classification. In [22], a bilateral awareness network for semantic segmentation was developed to increase the image resolution and improve the classification performance of HSI. In [23], a feature reduction method called improving distribution analysis (IDA) was developed for reducing data complexity and dimensionality of hyperspectral images. The correlation between related data is increased and the distance between big and small data is decreased, followed by increasing the value’s location inside the group range of the hyperspectral images.

Using the above studies’ feature extraction methods provided novel results for HSI classification can increase the classification accuracy. However, they lead to increases in the time consumed and the storage resources used, especially in the 3D CNN-based models. Thus, there is a need to develop a feature extraction strategy that can fully extract more valuable spatial and spectral features and alleviate the computational burden and time and storage resources.

2.2. Hyperspectral Image Classification on Imbalanced Data

For HSI classification, a lot of research used classical pattern recognition, machine learning, and deep-learning models.

In [24], the authors introduced a CNN patch-free-based method for classification. A CNN content-guided model was proposed for HSI classification. Roy et al. developed a novel model named HybridSN. The model can extract the spectral features and the spatial features by combining the 3D convolutions and the 2D convolutions with lightweight spatial–spectral residual features to reduce the parameters used for the sample training process of classification [25]. The authors in [26] presented a 3D coordination attention-based learning method for HSI classification. In that approach, the attention mechanism can obtain the long-distance dependence of horizontal directions, spatial position, and the important difference between various spectral bands. AL-Alimi et al. [27] proposed a hyperspectral image classification framework adopting a meta-learner method for training multi-class datasets using hybrid and multi-size kernel convolutional neural networks. Ma et al. [28] presented a spatial–spectral kernels-based generation network for producing spatial and spectral kernels using image characteristics, which were utilized to enhance the classification accuracy.

Although such outstanding results were obtained by previous models solving classification issues, there is a need to propose a new approach which can tackle the issue of the class imbalance in HSI datasets. The class imbalance issue can make the classification result biased toward learning the information from the majority classes and ignoring the minority classes [29]. The classification measures, such as overall accuracy (OA), and Kappa metric, etc., can be poorly presented for minority classes.

Several methods have been developed to address the class imbalance issue [30,31]. For example, sampling-based approaches are widely adopted due to their simple structure. These approaches are often adopted for preprocessing the imbalanced datasets before training to achieve better classification accuracy. Solving the imbalanced dataset approaches can be divided into two types, namely, undersampling and oversampling methods [32].

The undersampling-based methods mainly decrease the samples in the majority class to rebalance the samples in datasets. Singh et al. [33] proposed a SMOTE and centroid-based clustering method for undersampling the majority of class samples in the HSI datasets. In the study [34], a random feature subspace was used to perform an oversampling method for training samples and data enhancement. An ensemble-based learning model was developed by merging random feature selection with a convolutional network for performing image classification.

The oversampling-based methods increase the number of instances in the minority class by data augmenting or sample replication methods. For instance, Zhu et al. [35] adopted the GAN model to produce new samples for training the network and enhancing classification accuracy. In [36], a multiple-category spatial–spectral-based GAN approach was proposed. Two generator cells were utilized to extract the spectral features and the spatial features for the adversarial objectives for various classes. In [37], the authors introduced a new Caps-TripleGAN model to generate new images using a 1D_3D GAN and then classified the hyperspectral images using a capsule net-based model. Xue [38] presented a GAN-based image classification model using a 3D convolutional network and a 3D convolutional residual network. Roy et al. [39] developed a 3D adversarial oversampling-based model for HSI classification. The image samples were produced using a 3D hyperspectral patch. Then, a 3D-CNN-GAN-based classifier was used to perform the classification task.

Overall, although the above classification methods obtained outstanding results, the 3D convolution-based approaches have several drawbacks. For instance, with the growing number of 3D convolutions, the consumed time is getting longer. In addition, the overwhelming features can lead to an overfitting issue and influence the classification accuracy. Although the methods mentioned above adopted adversarial training for classification, they did not provide an effective solution for the minority classes. Therefore, there is still a need to produce image samples for each class and try to solve the class imbalance issue in HSI datasets.

3. The Proposed Model

This section introduces our model, and the detailed structure of the proposal is illustrated in Figure 1.

Our model contains three modules, namely, a feature extraction module, a data-balancing module, and a classification module. Firstly, the hyperspectral image size is reduced, then the main spectral features and the spatial features are extracted to understand the implicit feature distribution of the hyperspectral images. Secondly, the real images, represented by spatial–spectral features, are fed to an autoencoder module. The image labels are input with the minority class images, and a labeled latent vector is generated for each minority class. Thirdly, the GAN model receives the labeled latent vector, which represents the image features and the real images, then generates synthetic images and, in turn, recognizes the real images from the synthetic images. Finally, the balanced images are fed into the classification model for performing classification and obtaining classification results.

3.1. Feature Extraction

For better capturing the features of HSI, the feature extraction process considers three steps: spatial feature extraction, spectral feature extraction, and feature fusion. Figure 2 illustrates the feature extraction module.

Spatial features can play a vital role in the classification accuracy of HSI. As shown in Figure 2, spatial feature extraction begins with selecting the suitable spatial window size for the images. The original size of hyperspectral images (H × W × D, indicate height, width, and bands for an HSI) is considered, and images with a new spatial window would be selected (become M × N × D). Then, the new-sized images are fed to the latent convolutional layers as input data. The 2D convolutional neural networks capture spatial features using reduced-size images.

Table 1. The parameters setting of convolution layers for spatial feature extraction.

Layer	Input Channels	Output Channels	Kernel Size	Previous Layer
Input	1	1
2D CNN 1	1	32	3 × 3	Input
carpooling 1	32	32	2 × 2	2D CNN 1
2D CNN 2	32	64	3 × 3	carpooling 1
maxpooling 2	64	64	2 × 2	2D CNN 2
2D CNN 3	64	512	3 × 3	maxpooling 2
FullConnected				2D CNN 3

illustrates the parameter settings of the convolutional layers for spatial feature extraction.

The proposed module of spatial feature extraction contains six layers, and the structure design is described in Table 1. An output of an ith layer is represented by a feature map with different output channels, which is fed to the next layer. For the sake of further enhancing the performance, the Mish learning function is utilized instead of ReLU, as the Mish function presented more accurate results than ReLU [40]. Mish can be calculated as the following equation [40]:

$$\mathrm{Mish}\left(\mathrm{x}\right)=\tanh (\ln (1+e^x\left)\right) \times \mathrm{x}$$

(1)

where x presents inputs, ln (·) indicates logarithmic function, whereas tanh (·) denotes the popular function calculated as in the following equation [40].

$$\tanh (\mathrm{x})=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

(2)

Once the ith layer’s structure is a convolution layer, a 2D CNN-based operation is performed using kernel size 3 × 3 to obtain features and outputs a feature map O_i. This process can be calculated as function (3) [41]:

$${\mathrm{O}}_i=\sigma ({\mathrm{O}}_{i-1}\ast {\mathrm{W}}_i+{\mathrm{b}}_i)$$

(3)

where $\sigma$(·) represents the Mish activation function, and ∗ is the convolution operation. Moreover, O_i−1 is the previous layer output, whereas W_i and b_i denote weights matrix and the bias term of the current layer i.

Once an ith layer is maxpooling, the input size of a feature map would be shortened by replacing a 2 × 2 sized neighborhood region with the region’s maximum value. The calculation process is performed as in Equation (4):

O_i = maxPool(O_i−1)

(4)

Once the ith layer is a full connected layer, the spatial features can be extracted and are ready for concatenating with spectral features. The spatial features are denoted as Feature_spatial. Mathematically, this step can be calculated as in Equation (5):

Feature_spatial=O_{full_connected} =σ(O_i−1 ∗ W_i +b_i)

(5)

Similar to the convolution layer above, O_i-1 denotes an output of the previous layer, whereas W_i and b_i represent weights matrix and the bias term of the current layer i.

Regarding spectral feature extraction, the principal components analysis decreases the dimensions number of the spectral domain. The new size of hyperspectral images would be reduced (the original size, H × W × D, becomes H × W × B, indicating height, width, and bands). The spectral extraction and spatial extraction have similar architecture as they contain six layers. In addition, Mish activation is utilized as the learning function in the convolutional layers as well. The only different aspect to the spectral features extraction module is to avoid the complexity of commutation, 1D convolutional neural networks are used instead of 2D convolutional neural networks. Finally, the fully-connected layer provides the spectral features, denoted by Feature_spectral.

For the sake of facilitating the classification process and enhancing the classification accuracy, the captured spatial features and the spectral features are required to be fused. Let Feature_spatial={Sp₁,Sp₂,…,Sp_n} represent the extracted spatial features and Feature_spectral={Spe₁,Spe₂,…,Spe_m} represent the captured spectral features of a pixel with b bands. Thus, a spatial–spectral feature (Feature_{spatial_spectral}) of a pixel is generated by stacking the spectral feature vector Feature_spectral with the spatial vector Feature_spatial, which can be obtained by the following equation:

Feature_{spatial_spectral}={Sp₁,Sp₂,…,Sp_n,Spe₁,Spe₂,…,Spe_m}

(6)

In this article, Feature_{spatial_spectral} is used as the feature of real images which would be fed into the data-balancing module and the image classification module.

3.2. Data Balancing

HSI datasets are considered imbalanced data in which there are majority class and minority classes. The majority class contains the largest image samples, whereas minority classes have fewer samples. This can lead to biased results and reduce classification accuracy. Thus, balancing samples for minority classes becomes vital. With the widespread use of GAN and autoencoder deep learning models in HSI data augmentation, this article adopted these two models to produce synthetic images for balancing minority classes. Figure 3 describes the main features of the data-balancing module.

3.2.1. Autoencoder Network

As depicted in Figure 3, the autoencoder network contains two sub-networks: the encoder and the decoder. The aim of the encoder is to oversample the images (image features) of the minority classes by producing new samples, as depicted in Figure 3. The spatial–spectral stacked features, Gaussian noise, and class information (labels) are fed to the encoder network. The image class having the largest samples is considered as a majority class, whereas other classes are labeled as minority classes. Therefore, the images’ number of the majority class would be captured and used to generate images and balance the shortage in minority classes.

Suppose the training set has k minority classes. Thus, the encoder network should have k encoder cells, one En_i cell for each minority class i. Each En_i cell generates Gen_Im_i samples, as Equation (7):

Gen_Im_i = Im_m − Im_i

(7)

where Im_m represents the samples number of majority class m and Im_i for minority class i, i ∈ [1, k]. Therefore, each En_i cell has the following inputs (Gen_Im_i, class label i, Gaussian noise, and spatial_spectral features of the class samples) and encodes them into a class latent vector z_i. Figure 4. describes the internal architecture of an encoder cell.

The encoder cell contains two convolutions and two maxpoolings, which are two-dimensional cells. The initial encoded vector obtained by the encoder i is the following Equation (8):

z_i = En_i(x_i) = q(z_i|x_i)

(8)

where x_i is the stacked features of the minority class _i, considering the Gaussian noise and the class label_i. After calculating mean µ with covariance ε from the stacked features, the class latent vector z_i is Equation (9) is generated by applying Equation (9) [42]:

z_i = µ_i + r ∗ exp(ε_i)

(9)

After extracting the class latent vector z_i for each minority class _i, the corresponding decoder De_i would be triggered and fed by the label latent vector z_i. Figure 5 describes the internal architecture of a decoder cell.

The encoder cell contains two transposed convolutions (two-dimensional cells). In the encoder and the decoder layers, the ReLU activation function is applied, and the Adam algorithm is chosen as the optimization function. The aim of the decoder De_i is to learn the training data distribution, then produce image samples.

$$\stackrel{-}{x_{\mathrm{i}}}=\mathrm{Dec}({\mathrm{z}}_{\mathrm{i}})=\mathrm{p}({\mathrm{x}}_{\mathrm{i}}|{\mathrm{z}}_{\mathrm{i}})$$

(10)

where $\overline{x_i}$ is the generated samples from the label latent vector z_i. Finally, we obtain a set of synthetic images for each minority class _i.

3.2.2. Generative Adversarial Networks (GAN) Network

In general, the architecture of a GAN contains two subnetworks, namely, generator network and discriminator network. The generator network obtains image features and generates synthetic images. In contrast, the discriminator network obtains synthetic images, and distinguishes the synthetic images from the real images, and accordingly modifies the loss function until no difference can be found between generated and real images.

For the sake of decreasing the time complexity of implementing our model and for simplifying the model design with no influence on model functions, we consider the decoder network of the autoencoder module as the generator network of the GAN module. In addition, the decoder network generates image samples for minority classes, as the generator network should do in the GAN module. Thus, we focus on the discriminator network. Figure 6 illustrates the discriminator network design.

According to Figure 6, the discriminator network includes three convolution layers, and all of these layers are two-dimensional layers. The first and second layers apply the ReLU activation, whereas the last layer utilizes the sigmoid activation to distinguish image’ types (real or synthetic). More details about the 2D discriminator design are introduced in

Table 2. Parameters setting of convolution layers for the discriminator network.

Layer	Input Channels	Output Channels	Kernel Size	Previous Layer
2D Conv_1	32	32	3 × 3
2D Conv_2	32	64	3 × 3	2D Conv_1
2D Conv_3	64	512	3 × 3	2D Conv_2
FullConnected				2D Conv_3

.

The discriminator network receives the synthetic images generated by the decoder network and the real images as the input data. With the synthetic and real images, each image class becomes balanced, can increase the classification results, and performs image classification well. Therefore, the balanced images, including synthetic and real images, would also be sent to the classification.

3.3. Classification Module

The classifier network plays a vital role in our proposed model because of the need to classify the whole balanced image samples (the synthetic and the real ones). Figure 7 describes the design of our classification network.

As depicted in Figure 7, the classifier network’s design is similar to the discriminator network, and the only difference is that the last convolution layer used the SoftMax function. The classifier network calculates the scores of each image class, which are later used to obtain the value of SoftMax loss. The training and testing process of the classification network are implemented as follows. Training samples of every balanced image class (the real images and the samples generated from the autoencoder module for the minority classes) were used to performing the classification process, and testing data is utilized for validating the classification accuracy for each classification model.

4. Experiment

This article aims to develop a classification model for HSI, considering the minority class issue in the image samples. Therefore, we use the autoencoder and the GAN model to generate samples, balance the image number for each minority class, and improve the classification performance.

4.1. Datasets

Our study used four hyperspectral imbalanced datasets [43] with various environmental settings to validate the performance of our model, including Indian Pines, Kennedy Space Center, Salinas, and Botswana. Here is a short description of the datasets.

• The Indian Pines dataset is collected using the AVIRIS sensor in the Indian Pines area, Indiana. The dataset includes 224 bands with range wavelength of 0.4–2.5 × 10 ⁻⁶ m. Image size is 145 × 145 pixels [43]. More details of the classes and samples of Indian Pines are listed

  Table 3. Classes information of Indian Pines dataset.

  Number	Land Cover Class	Samples
  1	Alfalfa	46
  2	Corn notill	1428
  3	Corn-mintill	830
  4	Corn	237
  5	Grass-pasture	483
  6	Grass-trees	730
  7	Grass-pasture-mowed	28
  8	Hay-windrowed	478
  9	Oats	20
  10	Soybean-notill	972
  11	Soybean-mintill	2455
  12	Soybean-clean	593
  13	Wheat	205
  14	Woods	1265
  15	Buildings Grass Trees-Drives	386
  16	Stone-Steel-Towers	93

  and displayed om Figure 8.
• The Salinas dataset is collected using AVIRIS sensor in the Salinas area, California. The Salinas dataset includes 204 bands, and the image size is 512 × 217 pixels [43].

  Table 4. Classes information of Salinas dataset.

  Number	Land Cover Class	Samples
  1	Brocoli_green_weeds_1	2009
  2	Brocoli_green_weeds_2	3726
  3	Fallow	1976
  4	Fallow_rough_plow	1394
  5	Fallow_smooth	2678
  6	Stubble	3959
  7	Celery	3579
  8	Grapes_untrained	11,271
  9	Soil_vinyard_develop	6203
  10	Corn_senesced_green_weeds	3278
  11	Lettuce_romaine_4wk	1068
  12	Lettuce_romaine_5wk	1927
  13	Lettuce_romaine_6wk	916
  14	Lettuce_romaine_7wk	1070
  15	Vinyard_untrained	7268
  16	Vinyard_vertical_trellis	1807

  introduces more details about the land cover classes along with samples in the Salinas dataset, whereas Figure 9 shows the ground truth map and pseudo color image by Salinas dataset.
• The Kennedy Space Center dataset is gathered using NASA AVIRIS at the Kennedy Space Center area in Florida. The KSC dataset contains 224 spectral reflectance bands, and image size is 512 × 614 pixels [43].

  Table 5. Classes information of KSC dataset.

  Number	Land Cover Class	Samples
  1	Scrub	761
  2	Willow swamp	243
  3	CP hammock	256
  4	Slash Pine	252
  5	Oak/Broadleaf	161
  6	Hardwood	229
  7	Swap	105
  8	Graminoid marsh	431
  9	Spartina marsh	520
  10	Cattail marsh	404
  11	Salt marsh	419
  12	Mud flats	503
  13	Water	927

  listed the classes and the samples’ information of the KSC dataset, whereas the corresponding ground truth map and pseudo color image are depicted in Figure 10.
• By NASA EO-1 satellite, the Botswana dataset is gathered across the Okavango delta site. The dataset includes 242 spectral reflectance bands, and the image size is 1496 × 256 pixels.

  Table 6. Classes information of the Botswana dataset.

  Number	Land Cover Class	Samples
  1	Water	270
  2	Hippo Grass	101
  3	Floodplain Grasses1	251
  4	Floodplain Grasses2	215
  5	Reeds1	269
  6	Riparian	269
  7	Firescar2	259
  8	Island interior	203
  9	Accacia woodlands	314
  10	Accacia grasslands	248
  11	Short mopane	305
  12	Mixed mopane	181
  13	Exposed soils	268

  details the classes and the samples in the Botswana dataset. Figure 11 illustrates the ground truth map along with a pseudo color image for the Botswana dataset.

4.2. Experiment Settings

The experiments in this article were performed on a PC having Intel i7-10750 h with 32 GB RAM. RTX 2070 GeForce GPU with 11-GB memory. In addition, the Ubuntu 20 operating system was used for all experiments. Pytorch 1.11, cuDNN 8.4.1 and CUDA 11.3, matplotlib, and python 3.8 were the tool programming utilized in our experiments. All models performed by our experiments were applied on Anaconda 3.5 programming environment. Moreover, Earthpy, a transparent deep learning library, was used to provide for Earth dataset analytics. Platforms, such as TensorFlow, Keras, and Pandas, were combined into the core framework for processing and supporting the deep learning methods included in the proposed model.

4.3. Training Settings

The weights for the layers in our proposed model were randomly initialized, and the model parameters were updated by applying the Adam optimizer [44], along with a learning rate 0.0002. The maximum number of epochs was assigned to 400 for all datasets.

In our model’s training process, each experiment was run 4000 iterations, and once the generalization of the synthetic images of the minority classes became stable, the process terminated. A 25 × 25 × D spatial window was selected for the four datasets, where D represents the bands’ number.

Table 7. Samples information of the training and testing process of four datasets.

No	Indian Pines				Salina				KSC				Botswana
	Train			Test	Train			Test	Train			Test	Train			Test
	Real	Synth	Total		Real	Synth	Total		Real	Synth	Total		Real	Synth	Total
1	46	1454	1500	375	2009	5491	7500	1875	761	139	900	225	270	50	320	80
2	1428	72	1500	375	3726	3774	7500	1875	243	657	900	225	101	219	320	80
3	830	670	1500	375	1976	5524	7500	1875	256	644	900	225	251	69	320	80
4	237	1263	1500	375	1394	6106	7500	1875	252	648	900	225	215	105	320	80
5	483	1017	1500	375	2678	4822	7500	1875	161	739	900	225	269	51	320	80
6	730	770	1500	375	3959	3541	7500	1875	229	671	900	225	269	51	320	80
7	28	1472	1500	375	3579	3921	7500	1875	105	795	900	225	259	61	320	80
8	478	1022	1500	375	7500	0	7500	1875	431	469	900	225	203	117	320	80
9	20	1480	1500	375	6203	1297	7500	1875	520	380	900	225	314	6	320	80
10	972	528	1500	375	3278	4222	7500	1875	404	496	900	225	248	72	320	80
11	1500	0	1500	375	1068	6432	7500	1875	419	481	900	225	305	15	320	80
12	593	907	1500	375	1927	5573	7500	1875	503	397	900	225	181	139	320	80
13	205	1295	1500	375	916	6584	7500	1875	900	0	900	225
14	1265	235	1500	375	1070	6430	7500	1875
15	386	1114	1500	375	7268	232	7500	1875
16	93	1407	1500	375	1807	5693	7500	1875

lists the distribution of training (Train) and synthetic samples (Synth), and the test samples (Test) of the four datasets. As shown in Table 7, the number of samples of the training and testing process were different for each dataset. For example, due to Indian Pines having the biggest number of samples, Soybean-mintill was considered the majority class. In the experiment, we considered 1500 samples as the sample number for the real training dataset. Other classes were considered minority classes that need to generate synthetic samples and rebalance the sample number of every minority class. The testing samples number considered 1/4 of the training samples for each dataset. The same settings were conducted for the classes in the other datasets, and more details are described in Table 7.

4.4. Comparation Models and Evaluation Metrics

For studying the effectiveness of our proposed model on imbalanced datasets, we conducted model comparisons over several traditional classifiers, such as MLP [44], RF [45], SVM [46], Ada Boost [47], KNN [48], and DT [49] over machine learning methods, including LSTM [50], CNN1D [51], and CNN3D [52], and over existing outstanding classifiers, such as HybridSN [25] and 3D_Hypergamo [39]. The HybridSN model combines 3D and 2D convolution models for HSI classification. The spatial–spectral features are extracted by 3D and 2D convolutions, respectively. The 3D_Hypergamo utilizes a 3D-generator network which contains conditional feature mapping units, namely 3D hyperspectral patches, to generate new samples for each class, and a 3D classifier is also used to classify the samples (real and generated) into the corresponding classes.

We estimate the classification performance using popular evaluation metrics, namely, overall accuracy (OA), average accuracy (AA), and the kappa metric. The OA metric is calculated by considering the ratio of classified correctly images against total samples number in the testing dataset. The AA metric denotes the mean of the accuracies of image class, whereas the kappa metric denotes the weighting of the measured accuracies. Therefore, we expect that the synthetic samples produced by our model enhanced the classification performance and resulted in higher accuracy when comparing with existing HSI classifiers.

5. Experimental Results

5.1. Classification Results with Compared Models

The classification results of our model are compared with existing outstanding classifiers by the train–test datasets of the four used datasets.

It needs to be mentioned that obtaining classification results by using only the information in the articles of classifiers or obtaining details of the codes and the implementations is very difficult. A lot of parameters and details of implementation were not found in the articles and could only be obtained by guess once regenerating the experimental results.

Table 8. Comparison of classification performance of the compared models and our model.

Method	Indian Pines			Salinas			Botswana			KSC
	OA	AA	Kappa	OA	AA	Kappa	OA	AA	Kappa	OA	AA	Kappa
MLP [44]	90.21	93.11	88.72	92.17	88.38	89.59	80.34	80.19	78.67	71.12	72.79	75.58
RF [45]	83.14	85.15	81.14	83.63	81.23	78.32	83.59	84.99	82.23	83.13	76.76	81.17
SVM [46]	88.32	93.75	87.50	86.36	84.19	81.95	86.25	87.16	85.10	80.51	79.15	78.89
Ada Boost [47]	92.74	96.43	92.44	83.80	71.29	77.69	78.54	77.87	76.71	76.82	77.95	78.12
KNN [48]	91.16	95.16	89.15	89.23	86.86	85.49	89.79	90.65	88.94	85.03	78.83	83.30
DT [49]	80.71	83.14	80.14	79.24	66.54	71.36	89.88	90.79	89.04	85.93	79.86	84.31
LSTM [50]	60.22	58.51	59.68	91.63	88.38	88.8	78.29	77.72	76.44	62.24	62.00	63.24
CNN1D [51]	93.31	96.44	92.31	92.02	89.38	89.31	89.57	90.75	88.71	90.89	86.45	89.85
CNN3D [52]	94.04	95.57	93.89	91.56	88.3	88.71	86.29	87.18	85.15	87.59	82.08	86.17
HybridSN [25]	92.34	95.36	91.46	95.07	93.6	93.46	90.23	91.37	89.42	90.29	85.06	89.18
3D_Hyperamo [39]	94.24	94.64	93.69	93.71	91.08	91.56	94.22	94.81	93.74	90.18	85.02	89.06
Our model	94.47	94.92	94.09	95.48	93.87	94.01	96.74	96.31	96.57	91.57	86.42	90.48

reports a summary of the accuracy results of the classification models. It compares state-of-the-art models by various popular metrics. The highest values are marked with bold across all models.

As shown in Table 8, once comparing our model with classifier models using the four HSI datasets, our model achieves higher results regarding the metrics OA, AA, and kappa.

The Salinas dataset presents a larger spatial size and has the highest number of spectral bands; therefore, the obtained classification accuracy of Salinas is higher. Regarding the Indian Pines dataset, the spatial size is smaller along with sixteen classes, which leads to a lower accuracy performance. The Botswana dataset provides the highest spatial size among all HSI datasets, Botswana presents the least samples regarding the maps of ground truth. Thus, the accuracy results in the Botswana dataset are larger than those in the Indian Pines dataset and the Salinas dataset. The KSC dataset has only thirteen image classes, which can make the classification task easier than that in the other HSI datasets, and its overall classification accuracy is still high (reaches 91.57).

Regarding the Indian Pines dataset, our model achieves significant performance improvements of at least 1.3% and 1.1% regarding the OA and the kappa compared with the models: HybridSN, CNN3D, and 3D_ Hypergamo, as shown in Table 8. Traditional classifiers, such as RF and DT, achieved lower OA accuracy results (80.71 and 83.14), and LSTM achieved the lowest accuracy (60.22), which may show that LSTM networks are unsuitable for the image classification task. The CNN1D and CNN3D achieved high results (OA:93.31, 95.57, AA: 96.44, 95.57, and Kappa: 92.31, 93.89). These two models took advantage of rich information obtained by spectral features and spatial features and then enhanced the accuracy results.

In the Salinas dataset, DT shows the worst performance (OA: 79.24, AA: 66.54, and Kappa: 71.36), and FT and Ada Boost performed better than the DT model. The non-deep-learning-based approaches, i.e., SVM, KNN, and LSTM, obtained higher results. Moreover, the proposed model outperformed the deep-learning-based approaches (CNN3D, HybridSN, and 3D_ Hypergamo) and achieved a high level of 95.48%, 93.87%, 99.3%, and 94.01% for OA, AA, and kappa, respectively.

Our model significantly enhanced OA, AA, and kappa by about 2.7% compared to the second- and third-best models (HybridSN and 3D_Hypergamo) by the Botswana dataset. The worst results are recorded by Ada Boost and LSTM, ranging from 76.44–78.54 of OA, kappa, and AA. The remaining models achieved good results for the three metrics as well.

Regarding the KSC dataset, our model achieved the highest classification results on OA: 91.57 and kappa: 90.48, and the highest value of AA (86.45) was obtained by the CNN1D model. As expected, again, deep-learning-based approaches, such as CNN3D, HybridSN, and 3D_Hypergamo, obtained high accuracy results as these methods can effectively reduce overfitting, and the used parameters can update well during the backpropagation process.

In addition to the results of quantitative classification, classification maps of different classification models were investigated by data visualization. Figure 12, Figure 13, Figure 14 and Figure 15 illustrate classification maps generated by performing the HSI classifiers on the Indian Pine, Salinas, KSC, and Botswana datasets. The areas with different changes were marked using red triangles.

Regarding classification maps generated for Indian Pines, models with lower accuracy, i.e., RF, DT, and LSTM, resulted in observed scatter points in the classification maps, such as in Figure 12c,g,h.

In the Salinas dataset, Figure 13c,f,g illustrated dark scatter points as a result of the misclassification of a lot of points located at the center of land-cover areas by the classifiers, such as RF, Adaboost, and DT.

Figure 14 shows a comparation of classification maps across various classifiers performed on the KSC dataset. Figure 15b,e, and color-changed scatter points in Figure 14h show the effect of the misclassification of many points by MLP, Adaboost, and LSTM.

Similar results are also observed for the Botswana dataset, as shown in Figure 15. The classification maps produced by our model are obviously better than those generated by the other models.

The classification performance of the spatial–spectral-based classifiers can easily outperform other HSI models. CNN3D, HybridSN, and 3D_Hypergamo adopted deep networks to learn features, which resulted in smoother and higher-quality classification maps. The classification maps generated by deep-learning-based models show far higher quality compared to other methods.

By comparing the ground truth maps with classification maps, our model obtained the highest accuracy results on almost all HSI datasets and achieved significant qualitative enhancement compared to other maps as well. In addition, our model can also help to enhance the uniformity of the land-cover areas as depicted in Figure 12, Figure 13, Figure 14 and Figure 15.

The results prove that our model enhances the feature extraction and training processes and obviously outperforms the other classifiers well.

5.2. Training and Complexity Time with the Compared Models

Figure 16 shows the classification accuracy and loss comparisons for 100 epochs for training and validation.

As shown in Figure 16, our model performs convergence slower than the HybridSN but faster than the 3D_Hypergamo. The proposed model converged at about 30 epochs, whereas the HybridSN and 3D_Hypergamo converged at about 40. The HybridSN method achieves faster results as its simple design of an internal network has three 3D CNN layers and one 2D CNN layer. The 3D_Hypergamo model has a GAN-based network that needs settings for a huge amount of hyperparameters, which slows the convergence. In our study, our model adopted an autoencoder and GAN-based network, leading to an acceptable convergence speed. Compared with the HybridSN model, our model required analysis and learning more parameters, leading to slower convergence.

A comparison of the efficiency computation in terms of training and testing times of our model along with HybridSN and 3D_ Hypergamo is listed in

Table 9. Training in minutes and testing in seconds over the four datasets by the compared models.

Dataset	HybridSN		3D_Hypergamo		Our Model
	Training (mins)	Testing (sec)	Training (mins)	Testing (sec)	Training (mins)	Testing (sec)
Indian Pines	2.3	2.1	2.6	2.1	2.2	1.8
Salinas	3.1	2.9	3.2	3.2	3.6	3.25
KSC	2.63	1.9	2.8	2.91	3.7	2.81
Botswana	3.1	2.9	3.34	2.5	2.7	2.18

. Our proposed model outperformed other models and needs less training time and testing time when compared to models HybridSN and 3D_Hypergamo.

Table 10. Comparison of the performance of our model with different spatial windows sizes.

Window	Indian Pines (%)	Salinas (%)	KSC (%)	Botswana (%)
19 × 19	95.32	95.82	95.38	95.89
21 × 21	96.87	96.19	96.73	97.83
23 × 23	97.92	97.45	96.66	97.38
25 × 25	98.22	99.11	99.62	99.78

shows the spatial dimension’s impact on our model’s performance on the four datasets. The 25 × 25 spatial dimensions obviously achieve better results and become the most suitable for the proposed model.

6. Discussion

By analyzing the results achieved by the experiments above, several conclusions are drawn as follows.

Firstly, 1D CNN and 2D CNN-based networks can achieve better results in feature extraction compared to other models, such as Ada Boost [47], LSTM [50], CNN1D [51], HybridSN [25], and 3D_Hypergamo [39], as listed in Table 10. Our approach applied 1D convolutional networks and 2D convolutional networks to obtain the spatial and the spectral features of HSI. Using 1D convolutional networks to properly extract rich spectral features, the learning process becomes more effective and easier to implement. In addition, PCA is utilized to decrease spectral dimensionality to a smaller size, reducing the time consumed for learning features information. A larger spatial window size (25 × 25) is used over a 2D convolutional network for extracting spatial features and obtaining rich information attributed to HSI, then increase the classification accuracy as shown in Table 10.

Secondly, an autoencoder-GAN-based model was adopted to generate new sample models and to rebalance image class samples. The autoencoder model was applied to generate synthetic samples for each minority class in HSI datasets. An encoder and decoder cell were dedicated to a specific minority class, and the generated samples can be validated and modified using the discriminator network in the GAN network. Therefore, the samples in the minority classes would be rebalanced, and the sample number could be the same as the majority class, which leads to better results, as we can find in Table 10 and Figure 12, Figure 13, Figure 14 and Figure 15.

Thirdly, deep-learning-based approaches, especially CNN-based approaches, achieved higher classification accuracy results than traditional classifiers, such as MLP [44], RF [45], SVM [46], Ada Boost [47], KNN [48], etc. This may be due to the deep networks applied for the training and testing. Models, such as HybridSN [25] and 3D_ Hypergamo [39], and our approach obtained the highest classification results. All these models designed deeper CNN models for extracting features and then efficiently learning these features.

Finally, our model can achieve the highest value of classification accuracy on four used datasets, visually producing cleaner image classification maps, as the mistaken pixel number is remarkably reduced.

7. Conclusions

This study presents a hypered deep-learning-based HSI generation and classification model for imbalanced data. The proposed model provides an oversampling approach for solving class imbalance issues. Our model has three modules, namely, a feature extraction module, a data-balancing module, and a classification module. In the feature extraction module, spatial feature extraction begins with the principal components analysis method to decrease the spatial domain dimensions. The PCA method is followed by a 2D CNN that captures spatial features. Regarding spectral feature extraction, a 1D CNN was adopted to extract HSI spatial features, and the process of two feature extractions was performed synchronously. The two obtained features were fused into one spatial–spectral feature vector for improving image generation and classification.

GAN and autoencoder deep learning models in the data-balancing module were applied to produce synthetic images for balancing minority classes. Using the GAN structure, an encoder cell and a decoder cell were constructed for each minority class to generate and compensate new images, rebalance the samples, and increase the samples number to be the same as in the related majority class. A 2D CNN-based classifier was adopted to categorize the balanced, synthetic, and real samples.

The proposed model was validated using four open-access datasets. The results were compared with existing outstanding HSI classifiers. The results of our model outperformed the other classifiers in most cases. Moreover, the performance of our model is more suitable for imbalanced sets. The classification maps visualized by our proposed model were more suitable and smoother than those generated by other classifiers.

Overall, the proposed oversampling approach on minority classes led our proposed approach to extract more relevant features from various image classes, enhance the classification results, and improve remote sensing applications.

In future work, we need to perform more efforts in the following promising research fields. Firstly, besides developing oversampling techniques for HSI classification, there is a need to consider undersampling techniques to tackle the imbalance of data issues for HSI classification. Secondly, we need to study the classification problem in a large-scale benchmark dataset and investigate the classification performance of the hyperspectral images. The existing datasets may not be enough for studying the HSI classification issue. Finally, image decompression is another research field that needs to be considered, as image decompression can reduce the time needed for the classification task.