A Long-Time Coherent Integration STAP for GEO Spaceborne-Airborne Bistatic SAR
Abstract
:1. Introduction
- We extend the bistatic signal model and the spatial filter to the cases of long SAT and various bistatic configuration. Based on this, the moving targets’ spatial signals can be accumulated coherently and the radial velocity can be estimated accurately.
- We propose a novel LTCI-STAP method to deal with the problem of high-order range migration and space-variant Doppler parameters in the GEO SA-BSAR system. Via the method, the moving targets are well focused, and their positions and velocities are accurately estimated.
2. GEO SA-BSAR Signal Model for Moving Target
2.1. Slant Range Model
2.2. Multichannel Signal Model
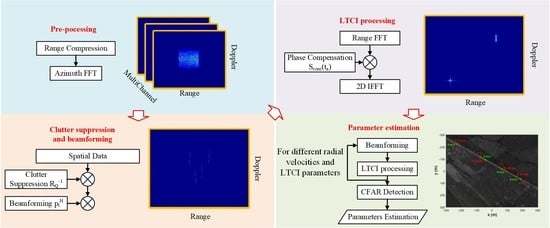
3. LTCI-STAP Method for GEO SA-BSAR MTI
3.1. Preprocessing Step
3.2. Clutter Suppression and Beamforming
3.3. LTCI Processing
3.4. Parameter Estimation
4. Simulation Experiments
4.1. Simulations of Single Point
4.2. Experiments with Scene Simulation
4.3. Computational Complexity Analysis
4.4. Parameter Estimation Accuracy Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Long, T.; Hu, C.; Ding, Z.; Dong, X.; Tian, W.; Zeng, T. Geosynchronous SAR: System and Signal Processing; Springer: Singapore, 2018. [Google Scholar]
- Hu, C.; Chen, Z.; Li, Y.; Dong, X.; Hobbs, S. Research progress on geosynchronous synthetic aperture radar. Fundam. Res. 2021, 1, 346–363. [Google Scholar] [CrossRef]
- Ruiz-Rodon, J.; Broquetas, A.; Makhoul, E.; Guarnieri, A.M.; Rocca, F. Nearly Zero Inclination Geosynchronous SAR Mission Analysis With Long Integration Time for Earth Observation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6379–6391. [Google Scholar] [CrossRef]
- Hobbs, S.; Sanchez, J.P. Laplace plane and low inclination geosynchronous radar mission design. Sci. China Inf. Sci. 2017, 60, 060305. [Google Scholar] [CrossRef]
- Li, Y.; Monti Guarnieri, A.; Hu, C.; Rocca, F. Performance and Requirements of GEO SAR Systems in the Presence of Radio Frequency Interferences. Remote Sens. 2018, 10, 82. [Google Scholar] [CrossRef] [Green Version]
- Santi, F.; Blasone, G.P.; Pastina, D.; Colone, F.; Lombardo, P. Parasitic Surveillance Potentialities Based on a GEO-SAR Illuminator. Remote Sens. 2021, 13, 4817. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J.; Yang, J.; Huang, Y.; Li, C.; Li, D. Path Planning for GEO-UAV Bistatic SAR Using Constrained Adaptive Multiobjective Differential Evolution. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6444–6457. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J.; Pei, J.; Li, Z.; Huang, Y.; Yang, J. Inclined Geosynchronous Spaceborne–Airborne Bistatic SAR: Performance Analysis and Mission Design. IEEE Trans. Geosci. Remote Sens. 2016, 54, 343–357. [Google Scholar] [CrossRef]
- Chen, J.; Sun, G.; Wang, Y.; Guo, L.; Xing, M.; Gao, Y. An Analytical Resolution Evaluation Approach for Bistatic GEOSAR Based on Local Feature of Ambiguity Function. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2159–2169. [Google Scholar] [CrossRef]
- Lian, M.; Jiang, Y.; Hu, B. Resolution analysis of GEO spaceborne-airborne bistatic SAR based on sliding spotlight mode. J. Syst. Eng. Electron. 2016, 27, 352–361. [Google Scholar] [CrossRef]
- An, H.; Wu, J.; Sun, Z.; Yang, J. A Two-Step Nonlinear Chirp Scaling Method for Multichannel GEO Spaceborne–Airborne Bistatic SAR Spectrum Reconstructing and Focusing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3713–3728. [Google Scholar] [CrossRef]
- An, H.; Wu, J.; Teh, K.C.; Sun, Z.; Yang, J. Nonambiguous Image Formation for Low-Earth-Orbit SAR With Geosynchronous Illumination Based on Multireceiving and CAMP. IEEE Trans. Geosci. Remote Sens. 2021, 59, 348–362. [Google Scholar] [CrossRef]
- Pu, W.; Wu, J.; Huang, Y.; Yang, J.; Yang, H. Fast Factorized Backprojection Imaging Algorithm Integrated With Motion Trajectory Estimation for Bistatic Forward-Looking SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3949–3965. [Google Scholar] [CrossRef]
- Zeng, Z.; Shi, Z.; Xing, S.; Pan, Y. A Fourier-Based Image Formation Algorithm for Geo-Stationary GNSS-Based Bistatic Forward-Looking Synthetic Aperture Radar. Sensors 2019, 19, 1965. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Y.; Yu, Z.; Li, J.; Li, C. Focusing Spotlight-Mode Bistatic GEO SAR With a Stationary Receiver Using Time-Doppler Resampling. IEEE Sens. J. 2020, 20, 10766–10778. [Google Scholar] [CrossRef]
- Guttrich, G.L.; Sievers, W.E. Wide Area Surveillance Concepts Based on Geosynchronous Illumination and Bistatic UAV or Satellite Reception. In Proceedings of the 1997 IEEE Aerospace Conference, Snowmass, CO, USA, 13 February 1997; Volume 172, pp. 171–180. [Google Scholar]
- Li, G.; Xu, J.; Peng, Y.; Xia, X. Bistatic Linear Antenna Array SAR for Moving Target Detection, Location, and Imaging With Two Passive Airborne Radars. IEEE Trans. Geosci. Remote Sens. 2007, 45, 554–565. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, W.; Dong, X.; Hu, C. A Novel Azimuth Spectrum Reconstruction and Imaging Method for Moving Targets in Geosynchronous Spaceborne–Airborne Bistatic Multichannel SAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5976–5991. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, Y.; Xing, M.; Guo, R.; Chen, J.; Liu, Y. Ground Moving Target Indication for the Geosynchronous-Low Earth Orbit Bistatic Multichannel SAR System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5072–5090. [Google Scholar] [CrossRef]
- An, H.; Wu, J.; Teh, K.C.; Sun, Z.; Yang, J. Simultaneous Moving and Stationary Target Imaging for Geosynchronous Spaceborne-Airborne Bistatic SAR Based on Sparse Separation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6722–6735. [Google Scholar] [CrossRef]
- Li, Y.; Wang, T.; Liu, B.; Yang, L.; Bi, G. Ground Moving Target Imaging and Motion Parameter Estimation With Airborne Dual-Channel CSSAR. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5242–5253. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Liu, B.; Zhang, S.; Nie, L.; Bi, G. A New Motion Parameter Estimation and Relocation Scheme for Airborne Three-Channel CSSAR-GMTI Systems. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4107–4120. [Google Scholar] [CrossRef]
- Kang, M.; Kim, K. Ground Moving Target Imaging Based on Compressive Sensing Framework With Single-Channel SAR. IEEE Sens. J. 2020, 20, 1238–1250. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J.; Li, Z.; An, H.; He, X. Geosynchronous Spaceborne-Airborne Bistatic SAR Data Focusing Using a Novel Range Model Based on One-Stationary Equivalence. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1213–1230. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I.; Gierull, C.H. Optimum SAR/GMTI Processing and Its Application to the Radar Satellite RADARSAT-2 for Traffic Monitoring. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3868–3881. [Google Scholar] [CrossRef]
- Ender, J.H.G. Space-time processing for multichannel synthetic aperture radar. Electron. Commun. Eng. J. 1999, 11, 29–38. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I. A generalization of DPCA processing for multichannel SAR/GMTI radars. IEEE Trans. Geosci. Remote Sens. 2013, 51, 560–572. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.; Liao, G.; Yang, Z.; Zhang, Y. Long-Time Coherent Integration Algorithm for Radar Maneuvering Weak Target With Acceleration Rate. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3528–3542. [Google Scholar] [CrossRef]
- Dong, X.; Cui, C.; Li, Y.; Hu, C. Geosynchronous spaceborne-airborne bistatic moving target indication system: Performance analysis and configuration design. Remote Sens. 2020, 12, 1810. [Google Scholar] [CrossRef]
- Jianwen, C.; Lei, R. Analysis of STAP on MDV for Spaceborne SAR-GMTI Applications. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–3. [Google Scholar]
















| System Parameters | GEO SAR Orbital Elements | ||
|---|---|---|---|
| Wavelength | 0.0566 m | Eccentricity | 0 |
| Bandwidth | 60 MHz | Inclination | 16° |
| Receiver’s Height | 10 km | Semimajor Axis | 42,164 km |
| Receiver’s Velocity | 200 m/s | Longitude Ascending Node | 113° |
| Synthetic Aperture Time | 3 s | ||
| Number of Channels | 10 | Argument of Perigee | - |
| Channel Spacing | 0.3 m | ||
| Configuration | 1 (Side Looking) | 2 (Squint-Forwards Looking) | 3 (Squint-Backwards Looking) |
|---|---|---|---|
| (deg) | 35 | 35 | 35 |
| (deg) | 0 | 30 | 330 |
| (deg) | 0 | 20 | 340 |
| Estimated Parameters | (s2/m) | (s2/m2) | (m) | (m) | |||
|---|---|---|---|---|---|---|---|
| Conf. 1 | 4.2 | −1.02 | 201.08 | 204.06 | 3.91 | 6.37 | |
| Conf. 2 | 4.8 | −1.00 | −0.001 | 199.61 | 190.14 | 4.16 | 5.89 |
| Conf. 3 | 3.7 | −1.02 | 200.05 | 196.93 | 4.05 | 5.98 |
| Target No. | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| x-axis (m) | −233 | −75 | 64 | 188 |
| y-axis (m) | −224 | −116 | −16 | 67 |
| (m/s) | −4.11 | 4.11 | 6.58 | −6.58 |
| (m/s) | −2.84 | 2.84 | 4.55 | −4.55 |
| Parameter | Configuration | T1 | T2 | T3 | T4 |
|---|---|---|---|---|---|
| (m) | Conf. 1 | −233.24 | −74.65 | 65.05 | 187.41 |
| Conf. 2 | −231.35 | −75.85 | 63.65 | 187.19 | |
| Conf. 3 | −233.82 | −74.23 | 62.69 | 188.61 | |
| (m) | Conf. 1 | −227.90 | −109.59 | −17.54 | 65.10 |
| Conf. 2 | −232.41 | −110.33 | −15.35 | 66.63 | |
| Conf. 3 | −239.28 | −109.42 | −19.40 | 63.62 | |
| (m/s) | Conf. 1 | −4.06 | 4.01 | 6.59 | −6.57 |
| Conf. 2 | −4.01 | 4.06 | 6.58 | −6.58 | |
| Conf. 3 | −3.89 | 4.02 | 6.64 | −6.54 | |
| (m/s) | Conf. 1 | −2.46 | 3.43 | 4.82 | −4.65 |
| Conf. 2 | −2.47 | 2.61 | 4.59 | −4.62 | |
| Conf. 3 | −3.17 | 2.90 | 4.60 | −4.81 |
| Parameter | Configuration | T1 | T2 | T3 | T4 |
|---|---|---|---|---|---|
| (m) | Conf. 1 | 0.24 | 0.35 | 1.05 | 0.59 |
| Conf. 2 | 1.65 | 0.85 | 0.35 | 0.81 | |
| Conf. 3 | 0.82 | 0.77 | 1.31 | 0.61 | |
| (m) | Conf. 1 | 3.90 | 6.41 | 1.54 | 1.90 |
| Conf. 2 | 8.41 | 5.67 | 0.65 | 0.37 | |
| Conf. 3 | 15.28 | 6.58 | 3.40 | 3.38 | |
| (m/s) | Conf. 1 | 0.06 | 0.10 | 0.01 | 0.01 |
| Conf. 2 | 0.10 | 0.06 | 0.01 | 0.02 | |
| Conf. 3 | 0.22 | 0.09 | 0.06 | 0.04 | |
| (m/s) | Conf. 1 | 0.38 | 0.59 | 0.27 | 0.10 |
| Conf. 2 | 0.37 | 0.23 | 0.04 | 0.07 | |
| Conf. 3 | 0.33 | 0.06 | 0.05 | 0.26 |
| SNR (dB) | −25 | −20 | −15 | −10 | −5 | 0 | |
|---|---|---|---|---|---|---|---|
| (m) | Conf. 1 | 1.01 | 1.20 | 0.99 | 1.35 | 0.99 | 0.89 |
| Conf. 2 | 0.83 | 0.39 | 0.0026 | 0.41 | 0.0026 | 0.041 | |
| Conf. 3 | 1.61 | 1.66 | 1.68 | 1.62 | 1.62 | 1.65 | |
| (m) | Conf. 1 | 6.23 | 10.47 | 1.70 | 7.95 | 1.89 | 8.12 |
| Conf. 2 | 3.84 | 9.56 | 15.72 | 9.67 | 15.72 | 9.66 | |
| Conf. 3 | 21.05 | 21.50 | 21.59 | 21.36 | 21.36 | 21.40 | |
| (m/s) | Conf. 1 | 0.087 | 0.07 | 0.17 | 0.0045 | 0.090 | 0.0016 |
| Conf. 2 | 0.074 | 0.16 | 0.25 | 0.16 | 0.25 | 0.16 | |
| Conf. 3 | 0.33 | 0.32 | 0.33 | 0.32 | 0.32 | 0.32 | |
| (m/s) | Conf. 1 | 0.27 | 0.91 | 0.24 | 0.47 | 0.33 | 0.27 |
| Conf. 2 | 0.18 | 0.14 | 0.12 | 0.11 | 0.12 | 0.11 | |
| Conf. 3 | 0.012 | 0.10 | 0.08 | 0.11 | 0.11 | 0.11 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, C.; Dong, X.; Chen, Z.; Hu, C.; Tian, W. A Long-Time Coherent Integration STAP for GEO Spaceborne-Airborne Bistatic SAR. Remote Sens. 2022, 14, 593. https://doi.org/10.3390/rs14030593
Cui C, Dong X, Chen Z, Hu C, Tian W. A Long-Time Coherent Integration STAP for GEO Spaceborne-Airborne Bistatic SAR. Remote Sensing. 2022; 14(3):593. https://doi.org/10.3390/rs14030593
Chicago/Turabian StyleCui, Chang, Xichao Dong, Zhiyang Chen, Cheng Hu, and Weiming Tian. 2022. "A Long-Time Coherent Integration STAP for GEO Spaceborne-Airborne Bistatic SAR" Remote Sensing 14, no. 3: 593. https://doi.org/10.3390/rs14030593
APA StyleCui, C., Dong, X., Chen, Z., Hu, C., & Tian, W. (2022). A Long-Time Coherent Integration STAP for GEO Spaceborne-Airborne Bistatic SAR. Remote Sensing, 14(3), 593. https://doi.org/10.3390/rs14030593