A Novel High-Squint Spotlight SAR Raw Data Simulation Scheme in 2-D Frequency Domain
Abstract
:1. Introduction
2. Models and Methods
2.1. Models
2.1.1. Broadside SAR
2.1.2. High-Squint SAR
2.2. Methods
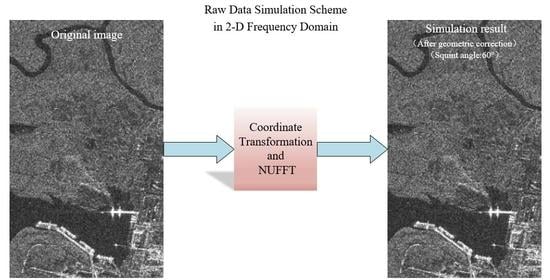
2.2.1. Coordinate Transformation
2.2.2. NUFFT
- (1)
- The window function is used to process the raw data and make the data relatively smooth;
- (2)
- The oversampling technique is used to calculate the Fourier transform;
- (3)
- The result from the second step and the window function are used to perform convolution processing.
2.2.3. Compensation of Range Walk
3. Experiment Results
3.1. Simulation Result
3.2. Performance Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, D.; Rodriguez-Cassola, M.; Prats-Iraola, P.; Wu, M.; Moreira, A. Reverse Backprojection Algorithm for the Accurate Generation of SAR Raw Data of Natural Scenes. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2072–2076. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Sun, J.; Lei, P.; Hong, W. SAR-Based Paired Echo Focusing and Suppression of Vibrating Targets. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7593–7605. [Google Scholar] [CrossRef]
- Niu, S.; Qiu, X.; Lei, B.; Ding, C.; Fu, K. Parameter Extraction Based on Deep Neural Network for SAR Target Simulation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4901–4914. [Google Scholar] [CrossRef]
- Tong, X.; Bao, M.; Sun, G.; Han, L.; Zhang, Y.; Xing, M. Refocusing of Moving Ships in Squint SAR Images Based on Spectrum Orthogonalization. Remote Sens. 2021, 13, 2807. [Google Scholar] [CrossRef]
- Huai, Y.; Liang, Y.; Ding, J.; Xing, M.; Zeng, L.; Li, Z. An Inverse Extended Omega-K Algorithm for SAR Raw Data Simulation With Trajectory Deviations. IEEE Geosci. Remote Sens. Lett. 2016, 13, 826–830. [Google Scholar] [CrossRef]
- Li, N.; Zhang, H.; Zhao, J.; Wu, L.; Guo, Z. An Azimuth Signal-Reconstruction Method Based on Two-Step Projection Technology for Spaceborne Azimuth Multi-Channel High-Resolution and Wide-Swath SAR. Remote Sens. 2021, 13, 4988. [Google Scholar] [CrossRef]
- Li, N.; Shen, Q.; Wang, L.; Wang, Q.; Guo, Z.; Zhao, J. Optimal time selection for ISAR imaging of ship targets based on time-frequency analysis of multiple scatterers. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Xing, M.; Wu, Y.; Zhang, Y.; Sun, G.; Bao, Z. Azimuth Resampling Processing for Highly Squinted Synthetic Aperture Radar Imaging with Several Modes. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4339–4352. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, M.; Li, J.; Wei, P. Modified Range-Doppler Algorithm for High Squint SAR Echo Processing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 422–426. [Google Scholar] [CrossRef]
- Chiang, C.-Y.; Chen, K.-S.; Yang, Y.; Zhang, Y.; Zhang, T. SAR Image Simulation of Complex Target including Multiple Scattering. Remote Sens. 2021, 13, 4854. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, Y.; Li, Z.; Liu, G.; Zhang, M. Simulation of a Wideband Radar Echo of a Target on a Dynamic Sea Surface. Remote Sens. 2021, 13, 3186. [Google Scholar] [CrossRef]
- Ku, C.; Chen, K.; Chang, P.; Chang, Y. Imaging Simulation for Synthetic Aperture Radar: A Full-Wave Approach. Remote Sens. 2018, 10, 1404. [Google Scholar] [CrossRef] [Green Version]
- Xiao, P.; Liu, M.; Guo, W.; Chen, W. Reconstruction of Synthetic Aperture Radar Raw Data under Analog-To-Digital Converter Saturation Distortion for Large Dynamic Range Scenes. Remote Sens. 2019, 11, 1043. [Google Scholar] [CrossRef] [Green Version]
- Qian, Y.; Zhu, D. Image Formation of Azimuth Periodically Gapped SAR Raw Data with Complex Deconvolution. Remote Sens. 2019, 11, 2698. [Google Scholar] [CrossRef] [Green Version]
- Ma, B.; Yu, B.; Liu, C.; Wang, Y. A 2-D Fourier Domain Algorithm for StripMap FMCW-SAR Raw Signal Simulation. J. Electron. Inf. Technol. 2011, 33, 375–380. [Google Scholar] [CrossRef]
- Wei, L.; Li, S.; Wu, Y.; Xiang, M. Performance Comparison of Algorithms for SAR Raw Signal Generation. J. Electron. Inf. Technol. 2005, 27, 262–265. [Google Scholar]
- Fu, Z.; Bai, L.; Guo, Z.; Min, L.; Li, N. Research on Acceleration Algorithm for Raw Data Simulation of High Resolution Squint Spotlight SAR. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2021), Brussels, Belgium, 11–16 July 2021; pp. 3281–3284. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, C.; Li, W.; Hu, W.; Wang, P.; Li, H. A Deep Collaborative Computing Based SAR Raw Data Simulation on Multiple CPU/GPU Platform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 387–399. [Google Scholar] [CrossRef]
- Zhang, F.; Yao, X.; Tang, H.; Yin, Q.; Hu, Y.; Lei, B. Multiple Mode SAR Raw Data Simulation and Parallel Acceleration for Gaofen-3 Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2115–2126. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, C.; Li, W.; Hu, W.; Wang, P. Accelerating Time-Domain SAR Raw Data Simulation for Large Areas Using Multi-GPUs. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3956–3966. [Google Scholar] [CrossRef]
- Jing, G.; Zhang, Y.; Li, Z.; Sun, G.; Xing, M.; Bao, Z. Efficient Realiazation of SAR Echo Simulation Based on GPU. J. Syst. Eng. Electron. 2016, 38, 2493–2498. [Google Scholar] [CrossRef]
- Franceschetti, G.; Schirinzi, G. A SAR Processor Based on Two Dimensional FFT Codes. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 356–366. [Google Scholar] [CrossRef]
- Franceschetti, G.; Migliaccio, M.; Riccio, D.; Schirinzi, G. SARAS: A Synthetic Aperture Radar (SAR) Raw Signal Simulator. IEEE Trans. Geosci. Remote Sens. 1992, 30, 110–123. [Google Scholar] [CrossRef]
- Franceschetti, G.; Migliaccio, M.; Riccio, D. On ocean SAR raw signal simulation. IEEE Trans. Geosci. Remote Sens. 1998, 36, 84–100. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lanari, R.; Marzouk, E. A New Two-Dimensional Squint Mode SAR Processor. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 854–863. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lodice, A.; Riccio, D.; Ruello, G.; Siviero, R. SAR Raw Signal Simulation of Oil Slicks in Ocean Environments. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1935–1949. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lodice, A.; Riccio, D.; Ruello, G. SAR Raw Singal Simulation for Urban Structures. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1986–1995. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lodice, A.; Perna, S.; Riccio, D. Efficient Simulation of Airborne SAR Raw Data of Extended Scenes. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2851–2860. [Google Scholar] [CrossRef]
- Franceschetti, G.; Guida, R.; Lodice, A.; Riccio, D.; Ruello, G. Efficient Simulation of Hybrid Stripmap/Spotlight SAR Raw Signals from Extended Scenes. IEEE Trans. Geosci. Remote Sens. 2006, 42, 2385–2396. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lodice, A.; Perna, S.; Riccio, D. SAR Sensor Trajectory Deviations: Fourier Domain Formulation and Extended Scene Simulation of Raw Signal. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2323–2334. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Deng, Y. Squint Spotlight SAR Raw Signal Simulation in the Frequency Domain Using Optical Principles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2208–2215. [Google Scholar] [CrossRef]
- Diao, G.; Xu, X. Fast Algorithm for SAR Raw Data Simulation with Large Squint Angles. J. Electron. Inf. Technol. 2011, 33, 684–689. [Google Scholar] [CrossRef]
- Li, G.; Ma, Y.; Hou, J.; Xu, G. Sub-aperture Keystone Transform Based Echo Simulation Method for High-squint SAR with a Curve Trajectory. J. Electron. Inf. Technol. 2020, 42, 2261–2268. [Google Scholar] [CrossRef]
- Breglia, A.; Capozzoli, A.; Curcio, C.; Liseno, A. NUFFT-Based Interpolation in Backprojection Algorithms. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2117–2121. [Google Scholar] [CrossRef]
- Hu, R.; Li, X.; Yeo, T.; Yang, Y.; Chi, C.; Zuo, F.; Hu, X.; Pi, Y. Refocusing and Zoom-In Polar Format Algorithm for Curvilinear Spotlight SAR Imaging on Arbitrary Region of Interest. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7995–8010. [Google Scholar] [CrossRef]
- Zhao, S.; Deng, Y.; Wang, R. Imaging for High-Resolution Wide-Swath Spaceborne SAR Using Cubic Filtering and NUFFT Based on Circular Orbit Approximation. IEEE Trans. Geosci. Remote Sens. 2016, 55, 787–800. [Google Scholar] [CrossRef]
- Capozzoli, A.; Curio, C.; Liseno, A. Optimized Nonuniform FFTs and Their Application to Array Factor Computation. IEEE T Antenn Propag. 2019, 67, 3924–3938. [Google Scholar] [CrossRef]
- Mukherjee, S.; Valenzise, G.; Cheng, I. Potential of Deep Features for Opinion-Unaware, Distortion-Unaware, No-Reference Image Quality. Lect. Notes Comput. Sci. 2020, 2015, 87–95. [Google Scholar] [CrossRef]









| Parameter | Value |
|---|---|
| Signal pulse width | 30 us |
| Pulse repetition frequency | 1500 Hz |
| Signal bandwidth | 50 MHz |
| Height | 10 km |
| Velocity | 200 m/s |
| Squint angle | 30°/45°/60° |
| Slant range of image center | 60 km |
| Center frequency | 9.65 GHz |
| Squint Angle | Algorithms | PSLR (dB) Azimuth/Range | ISLR (dB) Azimuth/Range |
|---|---|---|---|
| 30° | Time domain algorithm | −13.27/−13.26 | −11.34/−11.39 |
| Traditional squint algorithm | −12.81/−12.63 | −11.08/−11.13 | |
| Proposed algorithm | −13.16/−13.21 | −11.32/−11.28 | |
| 45° | Time domain algorithm | −13.23/−13.29 | −11.70/−11.28 |
| Traditional squint algorithm | −10.34/−10.89 | −10.59/−10.38 | |
| Proposed algorithm | −13.07/−13.13 | −11.46/−11.16 | |
| 60° | Time domain algorithm | −13.25/−13.21 | −11.59/−11.32 |
| Traditional squint algorithm | −7.62/−6.82 | −5.89/−6.38 | |
| Proposed algorithm | −12.89/−12.93 | −11.02/−10.87 |
| Squint Angle | Algorithms | Simulation Times (s) | ||
|---|---|---|---|---|
| 1 Target | 10 Targets | 100 Targets | ||
| 30° | Time domain algorithm | 3.27 | 33.55 | 329.68 |
| Traditional squint frequency algorithm | 0.37 | 0.69 | 2.87 | |
| Proposed algorithm | 0.41 | 0.66 | 2.91 | |
| 45° | Time domain algorithm | 3.67 | 35.75 | 332.13 |
| Traditional squint frequency algorithm | 0.43 | 0.77 | 2.93 | |
| Proposed algorithm | 0.39 | 0.68 | 2.88 | |
| 60° | Time domain algorithm | 3.87 | 37.53 | 339.53 |
| Traditional squint frequency algorithm | 0.45 | 0.73 | 3.05 | |
| Proposed algorithm | 0.42 | 0.61 | 2.91 | |
| Parameter | Value |
|---|---|
| Signal pulse width | 30 us |
| Pulse repetition frequency | 1300 Hz |
| Signal bandwidth | 60 MHz |
| Height | 5 km |
| Velocity | 400 m/s |
| Squint angle | 60° |
| Slant range of image center | 60 km |
| Center frequency | 9.65 GHz |
| Platform | Information |
|---|---|
| CPU | Inter Xeon Gold 6126 |
| Number of Core: 48 | |
| Clock Speed: 2.6 GHz | |
| Memory | 128 GB |
| Computing software | MATLAB 9.4 (R2018a) |
| Operating system | Windows 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Fu, Z.; Chang, J.; Wu, L.; Li, N. A Novel High-Squint Spotlight SAR Raw Data Simulation Scheme in 2-D Frequency Domain. Remote Sens. 2022, 14, 651. https://doi.org/10.3390/rs14030651
Guo Z, Fu Z, Chang J, Wu L, Li N. A Novel High-Squint Spotlight SAR Raw Data Simulation Scheme in 2-D Frequency Domain. Remote Sensing. 2022; 14(3):651. https://doi.org/10.3390/rs14030651
Chicago/Turabian StyleGuo, Zhengwei, Zewen Fu, Jike Chang, Lin Wu, and Ning Li. 2022. "A Novel High-Squint Spotlight SAR Raw Data Simulation Scheme in 2-D Frequency Domain" Remote Sensing 14, no. 3: 651. https://doi.org/10.3390/rs14030651
APA StyleGuo, Z., Fu, Z., Chang, J., Wu, L., & Li, N. (2022). A Novel High-Squint Spotlight SAR Raw Data Simulation Scheme in 2-D Frequency Domain. Remote Sensing, 14(3), 651. https://doi.org/10.3390/rs14030651