ClassHyPer: ClassMix-Based Hybrid Perturbations for Deep Semi-Supervised Semantic Segmentation of Remote Sensing Imagery

Abstract

Inspired by the tremendous success of deep learning (DL) and the increased availability of remote sensing data, DL-based image semantic segmentation has attracted growing interest in the remote sensing community. The ideal scenario of DL application requires a vast number of annotation data with the same feature distribution as the area of interest. However, obtaining such enormous training sets that suit the data distribution of the target area is highly time-consuming and costly. Consistency-regularization-based semi-supervised learning (SSL) methods have gained growing popularity thanks to their ease of implementation and remarkable performance. However, there have been limited applications of SSL in remote sensing. This study comprehensively analyzed several advanced SSL methods based on consistency regularization from the perspective of data- and model-level perturbation. Then, an end-to-end SSL approach based on a hybrid perturbation paradigm was introduced to improve the DL model’s performance with a limited number of labels. The proposed method integrates the semantic boundary information to generate more meaningful mixing images when performing data-level perturbation. Additionally, by using implicit pseudo-supervision based on model-level perturbation, it eliminates the need to set extra threshold parameters in training. Furthermore, it can be flexibly paired with the DL model in an end-to-end manner, as opposed to the separated training stages used in the traditional pseudo-labeling. Experimental results for five remote sensing benchmark datasets in the application of segmentation of roads, buildings, and land cover demonstrated the effectiveness and robustness of the proposed approach. It is particularly encouraging that the ratio of accuracy obtained using the proposed method with 5% labels to that using the purely supervised method with 100% labels was more than 89% on all benchmark datasets.

1. Introduction

With the recent increase in the number and availability of high-resolution remote sensing data, rapid and accurate extraction of semantic information from such data has received considerable focus in urban planning, agricultural monitoring, and disaster surveillance [1,2]. Traditional thresholding- and region-based methods can perform the image segmentation without requiring a large amount of labeled data, despite their coarse results [3]. Inspired by the success of deep learning (DL) in the computer vision field, the remote sensing community has also introduced this state-of-the-art technique into pixel-wise classification—also called semantic segmentation. Compared with traditional machine learning techniques—e.g., random forests or support-vector machines—DL is superior in that it automatically exploits feature representations solely from massive data, instead of handcrafting features based on domain-specific knowledge [4].

In general, supervised learning on massive labeled training data is the mainstream solution in DL due to its high accuracy and robustness [5]. However, the creation of labeled data is often time-consuming and expensive. Acquiring high-quality pixel-level labels for semantic segmentation in remote sensing applications is particularly challenging due to the great scene complexity. For example, Ji et al. [6] spent approximately six months creating their WHU building datasets (8188 labeled aerial images and 3742 labeled satellite images with 512 × 512 pixels), while Luo et al. [7] took nearly four months to annotate their aerial imagery shadow dataset (514 labeled images varied from 256 × 256 to 1688 × 1688 pixels). Both examples reflect the difficulty of labeling work for semantic segmentation in remote sensing, especially when faced with a growing number of Earth observation data from various platforms, such as satellites, airplanes, and UAVs.

To respond the challenge of labeled training data, an increasing number of studies have started investigating how to reduce labels while maintaining DL model performance—some of which have attempted to perform purely unsupervised learning based on time consistency between multitemporal remote sensing data [8,9]. These methods have a higher computing efficiency, but a lower accuracy in comparison to the methods using labeled training data. Moreover, a few studies [10,11] have paid more attention to image synthesis and translation within the scope of remote sensing, so as to produce more labeling data in a synthetic manner. However, the feature distribution of synthetic data is often inconsistent with that of real data due to a lack of specific control over the synthesis process. Moreover, low-quality reference data from OpenStreetMap [12] or cadastral maps [13] have also been used as labels for DL model training, although their performance is relatively poor. Recently, self-supervised learning paradigms such as contrastive learning have sought to characterize the latent space by decreasing and increasing the distances of intra- and interclass representations, respectively, from a mass of unlabeled data, and then apply this to downstream tasks, achieving impressive results in a range of applications despite requiring a huge amount of computational resources [14,15]. In addition to the abovementioned approaches, there are several widely used solutions with decent performance, e.g., transfer learning (TL), weakly supervised learning (WSL), and semi-supervised learning (SSL), which emphasize transferring the model capability from related tasks, or employing weak or few labels from the target of interest in training.

TL focuses on transferring knowledge learned from one annotation-rich domain (source domain) to a related but annotation-scarce domain (target domain), so as to improve the model’s availability across domains [16]. Typically, domain adaptation (DA) and parameter transfer are two popular schemes of TL in neural-network-based approaches [17,18]. DA aims to reduce the domain shifts of features in order to enable a pretrained model in the source data applicable to the unlabeled target data. Although DA has achieved progress recently, it remains challenging due to its relatively weak performance. Parameter transfer supposes that individual models for different but related tasks can share some parameters, thus allowing them to transfer across domains. In practice, parameter transfer is more extensively utilized because of its easy implementation and high effectiveness. Based on this strategy, remote sensing researchers have carried out a variety of applications such as land cover classification [19], scene classification [20], poverty mapping [21], and building extraction [22], in conjunction with limited task-dependent training data. Parameter-based TL has been widely used to alleviate labeled data deficiency, whereas challenges remain in overfitting and negative transfer [17]. As a result, parameter-based TL is usually paired with other techniques, such as WSL and SSL, to encourage the better performance of the DL model while using very few labels.

In the training process, WSL attempts to replace pixel-level labels with coarse annotations, such as box labels or image-level labels, in order to decrease human labeling effort. Chen et al. [23] proposed a WSL method using image-level labels as supervision information for building detection. Moreover, a weakly supervised feature-fusion network (WSF-Net) based on image-level annotations was developed to perform segmentation on water and cloud datasets [24]. These studies leveraged weak labels and achieved comparable results to purely supervised methods, thus exhibiting the utility of WSL methods in remote sensing image segmentation. WSL appears to be capable of reducing the annotation work to some extent. However, a mass of weak labels is still required during training, and pixel-level annotations can outperform weak ones in actual applications.

Unlike TL and WSL, SSL aims to train a model using datasets that have labels for only a fraction of their samples [5]. Most SSL approaches concentrate on either enlarging the data distribution to improve model generalizability, or learning latent features from the mass of unlabeled data to enable the decision boundary to be located in low-density regions [5,25]. It is worth noting that recent SSL approaches, such as Mean Teacher [26], CutMix [27], and FixMatch [28], have progressively pushed image classification performance to a high level in the computer vision field. In the meantime, the remote sensing community has also tried to investigate SSL in response to label deficiency in a wide range of applications, such as land cover classification [19], scene classification [29], and building extraction [15]. Notably, Hua et al. [30] presented a semi-supervised approach with sparse annotations for semantic segmentation of remote sensing images. In this method, the unsupervised loss was established based on the feature and spatial relational regularization, while the supervised loss was calculated using sparse annotation pixels in the form of points, lines, or polygons. This method achieved a decent trade-off between model performance and labeling efforts, despite the fact that the sparse annotations ignore the class boundary information. Following the classic dense-annotation pipeline, Wang et al. [31] proposed an SSL method (CRAUP) for remote sensing image segmentation that combines consistency regularization with random color jitter (similar to FixMatch) and average updates of pseudo-labels. To further improve the performance of SSL, Wang et al. [32] adopted the RanPaste algorithm (similar to CutMix) to enhance the data perturbation and incorporate Mean Teacher with pseudo-labeling methods in training, which can outperform the CRAUP method on different datasets. Note that these two studies involve the pseudo-labeling and consistency regularization scheme. Pseudo-labeling directly utilizes the predicted labels with high confidence from unlabeled data to guide the training process, which is a plug-and-play method that can be easily integrated with existing DL models [25]. However, determining the threshold of confident predictions remains an open question, and no universal method has been developed thus far. Furthermore, the training process of the pseudo-labeling method is unstable and cumbersome, leading to poorer results on multiclass segmentation tasks [31]. In contrast, the key idea behind consistency regularization is to encourage the model to give consistent predictions for unlabeled inputs perturbed in various ways [33]. Typically, this works by ensuring that the same input data with slight perturbations have a consistent output via the same model (data-level perturbation), or that the model with small perturbations generates consistent outputs for the same input data (model-level perturbation). For instance, slight changes in image contrast, color, and brightness should not have a significant impact on the final predictions for a deep semantic segmentation model, and models with the same architecture but different initiation parameters should obtain similar predictions on the same input. Generally, a good DL model should be robust and demonstrate strong generalization capability towards slight perturbations. Based on this strategy, the consistency loss can be constructed according to the differences between the outputs from the original inputs and their perturbed variants, allowing the unlabeled data to be used in the training process. Notably, this family of algorithms can leverage the pseudo-label information implicitly in the training stage, rather than explicitly using it in terms of the confidence value of the predictions, thereby avoiding the intractable step of confidence threshold setting and the negative effects of unhelpful predictions.

In order to explore the potential of the perturbation-based SSL pipeline on the basis of a dense-annotation paradigm, and to promote the model’s performance in remote sensing image semantic segmentation, we first illustrated several representative consistency learning schemes from the perspective of data- and model-level perturbation. Then, based on these schemes, we adapted an end-to-end semi-supervised semantic segmentation framework integrating cross pseudo supervision and ClassMix. The proposed approach was evaluated using five remote sensing benchmark datasets, and compared with several related perturbation-based schemes.

The major contributions of this study are as follows:

(1)

We comprehensively analyzed several prominent consistency-regularization-based approaches from the perspective of data- and model-level perturbation for deep semi-supervised semantic segmentation. To our knowledge, we are not aware of any study that has explored the consistency-regularization-based SSL approaches in remote sensing from this angle;

(2)

An end-to-end semi-supervised semantic segmentation framework adopting a hybrid perturbation paradigm—i.e., ClassHyPer—was introduced to improve the DL model’s performance for remote sensing image segmentation in the case of a limited number of labels;

(3)

Through the extensive experiments on five remote sensing benchmark datasets involving the segmentation of roads, buildings, and land cover, we demonstrated the effectiveness and robustness of ClassHyPer in remote sensing applications;

(4)

To further motivate the exploration and investigation in this field, we plan to make the related code publicly available at https://github.com/YJ-He/ClassHyPer (accessed on 2 January 2022).

2. Related Works

2.1. Semantic Segmentation for Remote Sensing

Thus far, the majority of DL-based semantic segmentation approaches perform pixel-wise dense predictions based on the fully convolutional network (FCN) architecture [34] and its multiple variants. Because of their superior performance in the computer vision field, FCN-based models were also introduced into pixel-level remote sensing image segmentation by the remote sensing community. With an increasing number of remote sensing annotation data and continuous improvement of computing power, there are a growing number of studies using FCN-based semantic segmentation approaches to extract buildings [6], roads [35], land cover [36], shadows [7], and clouds [37]. Ji et al. [6] developed a Siamese U-Net to extract buildings based on a self-created large remote sensing image dataset (WHU building dataset). The study’s findings demonstrated the high quality of the dataset and good performance of the new model, prompting many researchers to develop a vast number of FCN-based semantic segmentation models. A D-LinkNet [35] was proposed for road extraction, integrating the dilated convolution to enlarge the receptive field and ensemble multiscale features. The results from the DeepGlobe 2018 Road Extraction Challenge demonstrated its competitive performance. To improve the performance of the DL model in the complex urban scene, Zheng et al. [36] presented an EaNet for semantic segmentation, combining the edge-aware loss and large kernel pyramid pooling module. This approach accurately captures the multiscale semantic features in both ground and aerial urban scene datasets, such as Cityscapes [38], ISPRS Vaihingen [39], and the WHU Aerial Building dataset [6]. Furthermore, a deeply supervised convolutional neural network for shadow detection (DSSDNet) [7] was developed to extract shadows based on an aerial imagery dataset for shadow detection (AISD). Additionally, a pixel-wise cloud dataset [37] based on 18 Landsat-8 satellite images was created to evaluate the DL-based segmentation algorithms. It is clear that there has been an increase in the number of studies focusing on datasets created for DL-based semantic segmentation approaches. In turn, the increase in the number of datasets facilitates the continuous improvement of various algorithms. The development of algorithms and datasets keeps DL-related research and applications active and prosperous. All of these studies, however, rely on large amounts of labeled training data for good performance, which is still challenging in actual remote sensing applications.

2.2. Semi-Supervised Semantic Segmentation for Remote Sensing

Recently, some studies have attempted to improve the DL models’ performance by leveraging large amounts of unlabeled data in conjunction with a small fraction of labels based on the SSL pipeline for remote sensing image segmentation. The most critical component of SSL is the construction of unsupervised loss based on specific assumptions, which directs the training process with unlabeled data. Various unsupervised learning tasks have been designed to perform SSL. For example, the feature and spatial relations of pixels have been used to build the contrastive loss in remote sensing semantic segmentation with sparse annotations [30]. Protopapadakis et al. [40] adopted stacked autoencoders to learn the latent representations from a large number of unlabeled images. In addition, pseudo-labeling [41] works by iteratively leveraging the pseudo-labels for the unlabeled data needed to guide the training process. The unsupervised loss is formulated via the supervision from pseudo-labels to predictions. Evidently, pseudo-labeling is easy to implement by integrating existing DL models. Hence, this technique has been applied to numerous remote sensing applications. For example, Tong et al. [19] utilized pseudo-labeling to improve the transferability of deep models for land cover classification on satellite imagery. Li et al. [42] designed an SSL classification framework based on pseudo-labeling and conditional random fields for hyperspectral image classification and segmentation. Experimental results showed the effectiveness of pseudo-labeling in remote sensing applications. Nevertheless, extra methods are required in order to determine the threshold of confident predictions, and there is no one-size-fits-all method to date. Additionally, the training process might become unstable when the model generates many unhelpful predictions for unlabeled data with high confidence [43].

Consistency regularization is another class of algorithm developed for SSL, and contributes to the objective function by encouraging the predictions of the network to be consistent in the vicinity of the observed samples [5]. Due to its remarkable performance, the perturbation-based scheme has become one of the most effective consistency-regularization approaches. Regarding the task of image-level classification in the computer vision field, various approaches have been developed, including data-level perturbation (e.g., Cutout [44], MixUp [45], FixMatch [28]) and model-level perturbation (e.g., temporal ensembling [46] and Mean Teacher [26]). Meanwhile, data-level perturbation approaches (e.g., CutMix [27], CowMix [33], ClassMix [47], ComplexMix [48]), and model-level perturbation methods (e.g., guided collaborative training [49], cross-consistency training [50], cross pseudo supervision [51]) are booming in the semantic segmentation applications. With the significant advancement of SSL algorithms, a few remote sensing studies have tried to combine different techniques in SSL. For instance, Wang et al. [31] proposed a FixMatch-like approach incorporating pseudo-labeling and Mean Teacher for SSL-based remote sensing image segmentation. Subsequently, Wang et al. [32] further improved model performance on the basis of previous work [31], by integrating a CutMix-like scheme and pseudo-labeling. Although these studies have achieved progress in remote sensing semantic segmentation based on SSL, the use of pseudo-labeling schemes in their approaches makes the training process discrete and complex. Unlike pseudo-labeling methods, perturbation-based methods are more flexible and easier to integrate with the DL model in an end-to-end manner. In general, perturbation-based methods embed the consistency loss into the total cost function and optimize via training, rather than carrying out a separate process of training and retraining. Additionally, they do not require the determination of the confidence threshold, reducing the complexity and difficulty of the training process.

Reviewing the latest SSL methods for semantic segmentation, we find that augmentation-based approaches such as CutMix and ClassMix are prominent data-level perturbation schemes. At the same time, Mean Teacher and cross pseudo supervision are two typical representatives of the model-level perturbation pipelines. Inspired by these notable methods, we introduced an end-to-end hybrid perturbation approach, i.e., ClassHyPer, for semantic segmentation of remote sensing images, with dense annotations.

3. Methodology

3.1. Problem Definition

Given a set ${\mathcal{D}}_l=\left\{\left(x_1^l,y_1\right),\dots ,\left(x_N^l,y_N\right)\right\}$ of N labeled images and a set ${\mathcal{D}}_u=\left\{x_1^u,\dots ,x_P^u\right\}$ of P unlabeled images (P >> N), $x_i^u$ refers to the i-th unlabeled image, while $\left(x_i^l,y_i\right)$ represents the i-th labeled image with spatial dimensions $H\times W$ and its corresponding pixel-level label $y_i\in {ℝ}^{C\times H\times W}$, where C is the number of classes. The SSL semantic segmentation task aims to train a model by incorporating a small number of labeled data from ${\mathcal{D}}_l$ and a large amount of unlabeled data from ${\mathcal{D}}_u$, so that we can obtain a better model over the one using only labeled data.

Generally, traditional supervised learning for semantic segmentation only contains the supervision loss formulated by pixel-wise cross-entropy loss based on labeled images:

$${\mathcal{L}}_s=\frac{1}{\left|{\mathcal{D}}_l\right|}{\displaystyle \sum }_{x_i^l,y_i\in {\mathcal{D}}_l}CrossEntropy\left(y_i,f_{\theta }\left(x_i^l\right)\right)$$

(1)

where θ denotes the parameters of the DL model f.

During SSL, an unsupervised loss ${\mathcal{L}}_u$ is added based on the consistency regularization pipeline. As previously introduced, there are two classes of approaches: one is the data-level perturbation approach based on the perturbation of input data and their predictions, while the other is the model-level perturbation approach based on the perturbation of model parameters, whose loss terms can be formulated as Equations (2) and (3), respectively:

$${\mathcal{L}}_u=\frac{1}{\left|{\mathcal{D}}_u\right|}{\displaystyle \sum }_{x_i^u,x_j^u\in {\mathcal{D}}_u}d\left(f_{\theta }\left(g\left(x_i^u,x_j^u\right)\right),g\left(f_{\theta }\left(x_i^u\right),f_{\theta }(x_j^u)\right)\right)$$

(2)

$${\mathcal{L}}_u=\frac{1}{\left|{\mathcal{D}}_u\right|}{\displaystyle \sum }_{x_i^u,x_j^u\in {\mathcal{D}}_u}d\left(f_{\theta }\left(x_i^u,x_j^u\right),f_{\left(\theta +\eta \right)}\left(x_i^u,x_j^u\right)\right)$$

(3)

where $d$ (.,.) is a distance function that measures the differences between pre- and post-perturbation, and we can use cross-entropy or the mean squared error function, depending on specific situations; $g$ (.) represents the function perturbing the predictions from unlabeled images; $\eta$ denotes small perturbations adding to the model parameters. Finally, the integrated loss function $\mathcal{L}$ for SSL is the summation of supervised and unsupervised losses as Equation (4):

$$\mathcal{L}={\mathcal{L}}_{\mathrm{s}}+\lambda {\mathcal{L}}_u$$

(4)

where $\lambda$ > 0 denotes the trade-off weight, which controls the relative importance of the unsupervised term in the overall loss; we will set it to 1 empirically in later experiments. Based on the loss term $\mathcal{L}$, we can optimize the model parameters by utilizing gradient descent and backpropagation algorithms.

This study focuses on investigating four prominent consistency-regularization-based SSL approaches: two for data-level perturbation, and two for model-level perturbation. An end-to-end SSL method is then introduced based on a hybrid perturbation scheme.

3.2. Data-Level Perturbation

3.2.1. CutMix

CutMix [27] integrates the Cutout [44] and MixUp [45] methods, which cut one or more rectangular areas with random aspect and position from image A and paste them over image B to synthesize a new mixed image (Figure 1). Generally, CutMix is used as a data augmentation method in DL to expand training data size by producing more synthetic data. Here, it is used as a consistency-regularization-based method in the context of SSL by imposing perturbation on the unlabeled images and their predictions. The operation can be formulated as follows:

$$\tilde{x}=M\odot x_A+\left(1-M\right)\odot x_B$$

(5)

$$\tilde{y}=M\odot f_{\theta }\left(x_A\right)+\left(1-M\right)\odot f_{\theta }\left(x_B\right)$$

(6)

where $\left(\tilde{x},\tilde{y}\right)$ denote the synthetic image and prediction, respectively, based on unlabeled images $x_A$ and $x_B$; $M\in {\{0,1\}}^{W\times H}$ is a binary mask indicating where to cut out and fill in within two images; $\odot$ denotes element-wise multiplication, while 1 denotes a mask that is completely filled with ones; $f_{\theta }\left(x_A\right)$ and $f_{\theta }\left(x_B\right)$ denote outputs from the images $x_A$ and $x_B$ through DL model $f_{\theta }$, respectively, and θ represents the model parameters.

Thus, as shown in Equation (7), the consistency loss is calculated based on the differences between the mixed image’s prediction $f_{\theta }\left(\tilde{x}\right)$ and the mixed prediction $\tilde{y}$. Then, the consistency loss ${\mathcal{L}}_{cons}$ is integrated with the supervised loss ${\mathcal{L}}_s$ to train the model together using a gradient descent algorithm.

$${\mathcal{L}}_u={\mathcal{L}}_{cons}=\frac{1}{\left|{\mathcal{D}}_u\right|}{\displaystyle \sum }_{x_A,x_B\in {\mathcal{D}}_u}d\left(\tilde{y},f_{\theta }\left(\tilde{x}\right) \right)$$

(7)

3.2.2. ClassMix

ClassMix [47] can be regarded as the generalization of CutMix; the only difference between the two is how the mask M is generated. Instead of cutting and pasting rectangular areas, ClassMix cuts part of the predicted classes from image A and pastes it over image B, thus forming a synthetic image that can better preserve the semantic boundaries of the objects in image A. As shown in Figure 2, the mask is derived from the semantic boundary, making the mixed image more meaningful. In this way, the trained model can be robust not only to the change in the image’s context, but also to the diverse image occlusions. This approach has been applied to the Cityscapes dataset [38], which was created for algorithm testing of autonomous vehicle driving, and achieved better results than CutMix. The improvement can be attributed to two factors: (1) The diversity of the created masks, which stems from the fact that each image contains different classes and each class includes multiple objects, resulting in the varied masks in training. The increased diversity is helpful to enhance data distribution and promote the model’s generalization ability. (2) The masks are based on the semantics of the images, which respect the sematic boundaries of the original objects. Since the mixed borders lie closer to the actual semantic boundaries, the mixed images approach the real data distribution, making them more meaningful for training and prediction.

ClassMix is suitable for remote-sensing-related tasks due to its inherent consideration of semantic boundaries. Like CutMix, the consistency loss is based on the prediction of the mixed image $f_{\theta }\left(\tilde{x}\right)$ and the mixed prediction $\tilde{y}$. Regarding the mixture scheme, $x_A$ and $x_B$ are defined as the foreground and background images, respectively, which means that part of $x_A$ needs to be cut and pasted to $x_B$. Specifically, if there are more than two classes in $x_A$, half of the predicted classes are cut and pasted to $x_B$. If $x_A$ contains two classes, only the non-background class is cut out and pasted. If $x_A$ only contains the background class, then the mix will be ignored.

3.3. Model-Level Perturbation

3.3.1. Mean Teacher (MT)

Mean Teacher [26] was initially proposed for the image-level classification task, which performs SSL by building a consistency loss based on the predictions from the teacher model and student model (Figure 3). The key idea of MT is that an average of consecutive student models can represent a more accurate model than using the final weights directly. This technique has been used in remote sensing image semantic segmentation [31,32], and achieved considerable performance. Technically, the parameters of the teacher model are calculated based on the consecutive average of parameters of the student model given in Equation (8):

$${\theta }_t^{\prime }=\alpha {\theta }_{t-1}^{\prime }+\left(1-\alpha \right){\theta }_t$$

(8)

where $\alpha \in \left[0,1\right]$ is a smoothing coefficient, which is generally set to 0.99, while ${\theta }_t$ and ${\theta }_t^{\prime }$ represent the parameters of the student and teacher models in training step $t$, respectively.

Intuitively, the teacher and student models should produce consistent results, since there is only a tiny difference between their parameters. Hence, pseudo-labels from the teacher model can be used to supervise the predictions from the student model. Based on the MT scheme, a consistency loss is formed as Equation (9):

$${\mathcal{L}}_u={\mathcal{L}}_{cons}=\frac{1}{\left|{\mathcal{D}}_u\right|}{\displaystyle \sum }_{x\in {\mathcal{D}}_u}d\left(f_{{\theta }_t}\left(x\right),f_{{\theta }_t^{\prime }}\left(x\right)\right)$$

(9)

3.3.2. Cross Pseudo Supervision (CPS)

Cross pseudo supervision [51] is a recently proposed method that uses two models with the same architecture but different initialization parameters, and imposes mutual supervision to perform SSL (Figure 4). This approach aims to maintain consistency between two similar models with slight parameter perturbations. Two cross-consistency losses are built in the training process according to the cross-supervision operations as Equations (10) and (11). Thus, the unsupervised learning loss is calculated with the summation of two cross-consistency losses, as shown in Equation (12). This framework contains two supervised losses ${\mathcal{L}}_{\mathrm{s}1}$ and ${\mathcal{L}}_{\mathrm{s}2}$, for two trainable submodels that can be optimized. The total loss is formulated as Equation (13):

$${\mathcal{L}}_{cps1\_2}=\frac{1}{\left|{\mathcal{D}}_u\right|}{\displaystyle \sum }_{x\in {\mathcal{D}}_u}CrossEntropy\left(Y_1\left(x\right),f_{{\theta }_2}\left(x\right)\right)$$

(10)

$${\mathcal{L}}_{cps2\_1}=\frac{1}{\left|{\mathcal{D}}_u\right|}{\displaystyle \sum }_{x\in {\mathcal{D}}_u}CrossEntropy\left(Y_2\left(x\right),f_{{\theta }_1}\left(x\right)\right)$$

(11)

$${\mathcal{L}}_u={\mathcal{L}}_{cps1\_2}+{\mathcal{L}}_{cps2\_1}$$

(12)

$$\mathcal{L}={\mathcal{L}}_{\mathrm{s}1}+{\mathcal{L}}_{\mathrm{s}2}+\lambda {\mathcal{L}}_u$$

(13)

where ${\theta }_1$ and ${\theta }_2$ denote the respective parameters of two models with the same architecture $f$, and they are initialized with different values. $Y_1$ and $Y_2$ represent the one-hot label maps (called pseudo-segmentation maps) computed from the confidence probability results $f_{{\theta }_1}\left(x\right)$ and $f_{{\theta }_2}\left(x\right)$, respectively.

The model structure of CPS is slightly more complex but geometrically symmetrical, and implicit pseudo-supervision can be conducted between submodels without setting a confidence threshold. Note that its computation work is increased because two submodels need to be trained. Although this approach has achieved outstanding performance on two popular semantic segmentation datasets (Cityscapes [38] and PASCAL VOC 2012 [52]) in the computer science field, we still expect to explore its actual performance from the angle of remote sensing applications.

3.4. Hybrid Perturbation

Given the respective strengths of the data- and model-level perturbation, we argue that the combination of both schemes might further enhance model capability. Hence, to incorporate the benefits of both schemes, we designed a hybrid perturbation-based approach—i.e., ClassHyPer—by integrating ClassMix with CPS. Specifically, ClassMix is superior in generating mixed images that respect the semantic boundaries of the objects in the original images, which is helpful for the task of semantic segmentation. Moreover, the diversity of the masks broadens the scope of data distribution, thus resulting in the enhancement of the model’s generalization ability and the alleviation of the overfitting issue. The benefit of CPS lies in two aspects: One is that the consistency between two segmentation networks encourages the prediction decision boundary to be located in low-density regions. The other is that the perturbation of model parameters implicitly leverages the pseudo-segmentation map as the training signal for them to supervise one another, thus avoiding the intractable procedure of confidence threshold determination. In addition, both schemes can be easily embedded into existing DL models in an end-to-end manner, reducing the complexity and difficulty of model training.

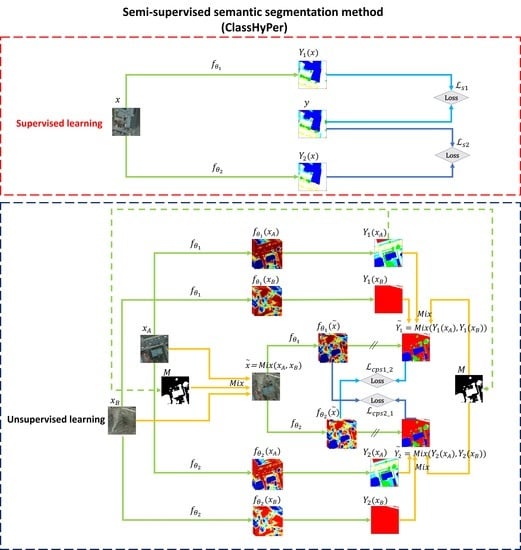
As illustrated in Figure 5, two unlabeled images are fed into two segmentation networks, and then the mask is generated according to one of the pseudo-segmentation maps. Subsequently, mixed inputs and outputs based on the mask are used to build consistency loss. Finally, a mass of cost-effective unlabeled data is capable of enhancing model performance via consistency learning. Beyond that, we also illustrate the method combining MT and ClassMix in Figure 6, which we used as a contrast method in later experiments. In the following section, relevant experiments are carried out to validate the effectiveness and robustness of ClassHyPer on different remote sensing datasets.

4. Experiments and Results

4.1. Datasets

To evaluate the effectiveness of the hybrid perturbation framework for semantic segmentation on remote sensing images, we chose five high-resolution remote sensing benchmark datasets for the experiments.

Table 1. Overview of the datasets used in the experiments.

Dataset	Labeled Images	Split (Train:Val:Test)	Classes	Size (Pixels)	Resolution (m)	Bands	Data Source
DG_Road	6226	3735:623:1868	2	512 × 512	1	R-G-B	Satellite
Massa_Building	1191	1065:36:90	2	512 × 512	1	R-G-B	Aerial
WHU_Building	8188	4736:1036:2416	2	512 × 512	0.3	R-G-B	Aerial
Potsdam	1368	612:252:504	6	512 × 512	0.1	R-G-B	Aerial
Vaihingen	1009	692:68:249	6	512 × 512	0.09	IR-R-G	Aerial

gives the overview of each dataset, and some examples of these datasets are shown in Figure 7.

DeepGlobe Road Extraction Dataset (DG_Road) [53]: This is an RGB satellite dataset created for a road and street network extraction challenge, which is to classify every pixel into binary categories (road and background); it contains 6226 labeled RGB satellite images with 1024 × 1024 pixels captured over Thailand, India, and Indonesia. In our experiments, we resized them to 512 × 512 pixels to reduce the computation, as described in [32], since the objective is to validate the performance of SSL rather than to obtain the best segmentation results in the challenge contest. Then, we randomly split them into three subsets as a ratio of 60%:10%:30% for training (3735), validation (623), and testing (1868), respectively;

Massachusetts Building Dataset (Massa_Building) [54]: This dataset contains 151 RGB aerial images of the Boston area, and corresponding building polygons from OpenStreetMap as ground truths. Each image is 1500 × 1500 pixels with a 1 m spatial resolution. We followed the official data split—137 for training, 4 for validation, and 10 for testing—then resampled them to 1536 × 1536 pixels using nearest-neighbor interpolation and, finally, cropped them into 512 × 512-pixel patches without overlap. After removing some images with blank data, 1065, 36, and 90 labeled images were obtained for training, validation, and testing, respectively;

WHU Aerial Building Dataset (WHU_Building) [6]: This is a large aerial RGB dataset for binary-class semantic segmentation (building and background), covering over 220,000 buildings of 450 km² with 0.3 m spatial resolution in Christchurch, New Zealand. The creator cropped the imagery into 8188 patches with 512 × 512 pixels seamlessly and then split them into three subsets: 4736 for training, 1036 for validation, and 2046 for testing. Due to the large sample volume and high labeling accuracy, this dataset has become one of the most popular benchmark datasets for DL-based building extraction in the remote sensing community. For the convenience of training, we followed the official data split scheme in our experiments;

ISPRS Potsdam 2D Semantic Labeling Dataset (Potsdam) [39]: This dataset is a subset of the ISPRS semantic labeling contest benchmark datasets, consisting of 38 aerial true orthophotos with 0.05 m spatial resolution and corresponding six-class ground-truth labels (i.e., impervious surfaces, buildings, low vegetation, trees, cars, and clutter/background). The original size of each patch is 6000 × 6000 pixels. Although RGB, IRRG, RGBIR, and DSM data are provided officially, we only used the three-channel RGB-labeled images in our experiments. Following the official suggestion, we divided them into training, validation, and testing subsets with 17, 7, and 14 labeled images, respectively. Due to the limited computing power, the raw images were resized to 3072 × 3072 pixels, and then cropped into 512 × 512-pixel patches without overlap. As a result, we obtained 612, 252, and 504 labeled images for training, validation, and testing, respectively;

ISPRS Vaihingen 2D Semantic Labeling Dataset (Vaihingen) [39]: This is also a subset of the ISPRS benchmark datasets, containing 33 patches with 0.09 m spatial resolution. Each patch involves a color-infrared orthophoto, DSM, and corresponding ground-truth label with six classes (the same as the Potsdam dataset). In our experiments, we only used the color-infrared orthophotos and corresponding labels. We also followed the official suggestion and chose 11, 5, and 17 patches as training, validation, and testing sets, respectively. All patches were cropped into 512 × 512 sub-patches. The only difference was that training samples were cropped with a 256 × 256 overlap, while the validation and testing samples were without overlap. Finally, 692, 68, and 249 sub-patches were acquired for training, validation, and testing, respectively.

4.2. Experimental Setup

All of the experiments were implemented via PyTorch 1.9.0 [55] with CUDA 10.2 in a single NVIDIA GeForce RTX 2080Ti GPU with 11 G memory. Data augmentation adopted random horizontal and vertical flip. An AdamW optimizer [56] with a weight decay of 0.0002 and momentum of 0.9 was employed because of its characteristics of fast convergence. The learning rate was initialized at 0.0001, and a one-cycle learning rate policy [57] was used for adjusting the learning rate in training. To avoid overfitting, we adopted the early stopping strategy, which guides training stops when maximum IoU does not improve over a few epochs. The batch size was set to four for all experiments to fit the GPU memory and ensure a fair comparison.

Regarding the mask generation in CutMix, we followed the scheme laid out in [5]. Three rectangles covering 50% of the image area with a random aspect ratio and position were used to create the masks. For the mask generation of ClassMix, a warmup strategy was adopted. Specifically, the model was first trained for a few epochs—e.g., 1/8 of the total training epochs—with only labeled data, so as to produce predictions with more accurate class boundaries in order to obtain more meaningful masks in training.

Following the general rule of thumb in model training, we used the training set to fit the model parameters, the validation set to evaluate the model and determine the best model parameters, and the testing set for final model evaluation. Furthermore, to perform the SSL experiments, we split the training set into two groups, randomly sub-sampling 5, 10, 20, or 50% of the whole set as the labeled subset, and the remaining data as the unlabeled subset. To reduce the randomness and ensure the reliability of the results, we repeated the random data sub-sampling three times for each dataset, and used the average value of evaluation metrics to evaluate the final model performance.

In addition, in order to avoid the unfair comparison between fully supervised and semi-supervised learning approaches, we followed the training rules described in [49]. First, we defined the total number of training samples as:

$$N=E\times T\times B$$

(14)

where $E$ represents the total training epochs, $T$ denotes the number of iterations in each epoch, and $B$ is the batch size—set to 4 in all experiments due to the limited GPU memory. The detailed training rules were as follows:

(1)

All purely supervised experiments were trained for 50 epochs, with 20-epoch early stopping. $T$ decreased with the decrease in the number of labeled data in the context of SSL, but to prevent overfitting, we did not increase $E$;

(2)

$E$ was adjusted to ensure that $N$ was the same as the fully supervised baseline using all labeled data. Since each batch in the SSL experiment involved labeled and unlabeled data, we defined an “epoch” in SSL experiments as going through the unlabeled data once, while the labeled subset was repeated a few times to match the number of unlabeled samples within an epoch;

(3)

Empirically, we used the adaptive early stopping strategy in SSL experiments to avoid collapsed training and overfitting. The epochs of early stopping were calculated by 0.4 × $E$.

4.3. Base Segmentation Model

Regarding the semantic segmentation model, a simple but classic FCN model (Figure 8) was chosen as the base model architecture; its encoder was replaced with the encoder of VGG16 [58], so that we could directly use the VGG16 model parameters trained on the ImageNet dataset [59]. This dataset is a very large benchmark dataset for 1000-class image recognition, containing over 1.2 million labeled images. Although it was created for image-level classification instead of pixel-level semantic segmentation, its encoder of the pretrained model can still extract the general features from images [20]. Through this parameter TL strategy, we can accelerate the training process and achieve better model performance, especially in the case of very few labeled data. Note that the designed SSL framework in this study can be integrated with other prominent DL semantic segmentation architectures. Nevertheless, considering that our objective was to evaluate the effectiveness of the proposed SSL approach, we only conducted experiments based on this model architecture in the study, due to the extremely time-consuming experimental work (see time efficiency in Section 5.1).

4.4. Evaluation Metrics

Commonly, there are several main quantitative evaluation metrics—e.g., precision, recall, F₁-score, and intersection over union ($\mathrm{IoU}$)—for pixel-level semantic segmentation. These metrics are related to four classifying conditions in prediction: true positive ($\mathrm{TP}$), false positive ($\mathrm{FP}$), true negative ($\mathrm{TN}$), and false negative ($\mathrm{FN}$), where $\mathrm{TP}$ is the correctly classified pixels, $\mathrm{FP}$ is the incorrectly classified pixels, $\mathrm{TN}$ is the correctly rejected pixels, and $\mathrm{FN}$ is the incorrectly rejected pixels.

$$\mathrm{IoU}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}+\mathrm{FN}}$$

(15)

Among them, $\mathrm{IoU}$ represents the intersection of the prediction and ground truth over the union of the whole image set, whose value ranges from 0 to 1; it can robustly evaluate the segmentation results even with the unbalanced number of classes in the datasets. For example, non-building pixels are far more numerous than building pixels in the Massa_Building dataset; $\mathrm{IoU}$ can still robustly measure the detection results in this unbalanced classification situation, which can take both the detection precision and completeness into consideration. Hence, $\mathrm{IoU}$ is used to evaluate the model performance in later experiments.

4.5. Experimental Results

To comprehensively assess ClassHyPer and other perturbation-based SSL approaches, we conducted experiments using purely supervised learning methods (Sup) and semi-supervised learning methods (SSL) with different proportions of labeled samples on multiple remote sensing datasets. Baseline denotes the method that uses the modified FCN model introduced in Section 4.3. TL means that the parameter transfer learning strategy was used. Specifically, the pretrained parameters of VGG 16 were transferred to the baseline model. Note that the TL strategy was applied to all SSL methods as well. Since the class imbalance problem usually exists for binary-class datasets (e.g., DG_Road, Massa_Building, and WHU_Building), we only considered the $\mathrm{IoU}$ of the target object (such as roads or buildings) for performance evaluation, without regard to the background. For multiclass datasets (e.g., Potsdam and Vaihingen), mean $\mathrm{IoU}$ ($\mathrm{MIoU}$) was adopted for accuracy assessment, which is the average value of the $\mathrm{IoU}$ of all classes. To simplify the expression, we use $\mathrm{IoU}$ to represent the accuracy uniformly later, whether the dataset is for binary-class segmentation or not.

4.5.1. DG_Road

DG_Road is a road extraction dataset based on satellite imagery with two classes: road and background. From the quantitative results shown in

Table 2. Accuracy ($\mathrm{IoU}$, %) comparison of different methods on the DG_Road dataset, where the values in bold are the best for each proportion.

Method		5% (186)	10% (373)	20% (747)	50% (1867)	100% (3735)
Sup	Baseline	46.65 ± 0.54	50.72 ± 0.83	55.80 ± 0.27	60.15 ± 0.25	62.97 ± 0.07
	TL	52.88 ± 0.39	56.76 ± 0.11	59.34 ± 0.25	62.49 ± 0.21	64.73 ± 0.38
SSL	CutMix	55.63 ± 0.33	58.33 ± 0.33	60.62 ± 0.11	62.52 ± 0.27
	ClassMix	55.06 ± 0.49	58.05 ± 0.42	59.96 ± 0.26	61.85 ± 0.02
	MT	51.70 ± 0.87	54.66 ± 0.68	58.01 ± 0.66	61.60 ± 0.13
	MT+CutMix	55.85 ± 0.47	58.74 ± 0.24	60.75 ± 0.07	62.10 ± 0.13
	MT+ClassMix	54.23 ± 0.60	57.50 ± 0.83	59.87 ± 0.20	60.75 ± 0.36
	CPS	52.10 ± 1.16	56.77 ± 1.00	59.27 ± 0.60	62.00 ± 0.12
	CPS+CutMix	58.88 ± 0.46	60.53 ± 0.48	61.77 ± 0.18	63.19 ± 0.27
	ClassHyPer	57.92 ± 0.26	60.03 ± 0.28	61.14 ± 0.13	62.56 ± 0.09

, we can see that both TL and SSL can improve the model performance over the baseline. There is a relatively higher accuracy promotion, especially when using very few labeled data. When using 5% labeled data (186 labeled images), TL and the best SSL approach (CPS+CutMix) increase the average $\mathrm{IoU}$ from 46.65 to 52.88 and 58.88%, respectively, which is a huge improvement in the semantic segmentation task. In addition, the data-level perturbation approaches (CutMix and ClassMix) can significantly improve the model accuracy over TL with very few labels. In contrast, the model-level perturbation approaches (MT and CPS) cannot do the same thing, despite their higher accuracy than baseline. CPS-based hybrid perturbation approaches have better performance, but MT-based hybrid perturbation approaches cannot even outperform data-level perturbation approaches alone. Among the CPS-based hybrid approaches, the accuracy of ClassHyPer is slightly lower than that of CPS+CutMix. This might be attributed to the fact that the ClassMix-based method is not appropriate for road extraction, due to the extremely sparse distribution of road targets with linear characteristics. Furthermore, it is worth noting that our model’s performance is much better than the recent RanPaste method [32] on this dataset. For instance, ClassHyPer achieved around 60% $\mathrm{IoU}$ with 373 labels, while RanPaste obtained 54.24% $\mathrm{IoU}$ with 400 labels. As seen from Figure 9, the visualization result also correlates well with the quantitative analysis. CPS+CutMix had the fewest false negative (yellow color) and false positive (red color) pixels compared with other approaches.

4.5.2. Massa_Building

Massa_Building is an aerial imagery building extraction dataset with 1 m spatial resolution, and involves two classes: building and background. As shown in

Table 3. Accuracy ($\mathrm{IoU}$, %) comparison of different methods on the Massa_Building dataset, where the values in bold are the best.

Method		5% (53)	10% (106)	20% (212)	50% (532)	100% (1065)
Sup	Baseline	57.35 ± 1.31	63.60 ± 0.75	65.71 ± 0.06	69.51 ± 0.28	71.73 ± 0.28
	TL	65.05 ± 0.98	68.21 ± 0.32	69.78 ± 0.36	71.48 ± 0.57	73.15 ± 0.12
SSL	CutMix	66.32 ± 1.49	70.07 ± 0.83	70.98 ± 0.61	71.67 ± 0.37
	ClassMix	68.98 ± 0.40	69.94 ± 0.77	70.60 ± 0.38	71.39 ± 1.21
	MT	63.27 ± 2.36	67.35 ± 0.68	69.64 ± 0.86	71.18 ± 0.87
	MT+CutMix	66.54 ± 1.52	70.05 ± 0.86	70.73 ± 0.39	72.18 ± 0.45
	MT+ClassMix	67.98 ± 1.38	70.35 ± 0.03	70.79 ± 0.57	71.82 ± 0.49
	CPS	66.75 ± 0.64	69.17 ± 1.05	70.54 ± 0.54	70.84 ± 0.40
	CPS+CutMix	69.03 ± 1.26	71.08 ± 0.55	71.77 ± 0.34	71.92 ± 0.57
	ClassHyPer	69.85 ± 0.25	71.62 ± 0.51	72.17 ± 0.47	72.31 ± 0.38

, the quantitative results are similar to those from the DG_Road dataset. Baseline has the lowest accuracy at each proportion of labeled data, while TL and SSL can improve the accuracy using very few labels. When using 5% labeled data (53 labeled images), TL and the best SSL approach (ClassHyPer) significantly increase the $\mathrm{IoU}$, from 57.35 to 65.05 and 69.85%, respectively. The data-level perturbation methods can achieve better results than model-level perturbation methods. Furthermore, the TL approach using 100% labeled data has the best performance (73.15%), while the accuracy of ClassHyPer using 50% labeled data (72.31%) is not far behind. However, unlike the results of the DG_Road dataset, ClassMix is more effective than CutMix on this dataset. ClassHyPer obtains the best accuracy in all proportion subsets, indicating that the increasing diversity of scenes and the consideration of class boundary information can motivate the potential of SSL algorithms. Visually, Figure 10 also demonstrates the superiority of SSL approaches on this dataset with only 5% labels, in which ClassHyPer achieves the best extraction results (more green, less yellow and red pixels).

4.5.3. WHU_Building

WHU_Building is a large building extraction dataset with 0.3 m spatial resolution, containing two classes (building and background). The quantitative results are shown in

Table 4. Accuracy ($\mathrm{IoU}$, %) comparison of different methods on the WHU_Building dataset, where the values in bold are the best.

Method		5% (236)	10% (473)	20% (947)	50% (2368)	100% (4736)
Sup	Baseline	81.65 ± 0.52	84.48 ± 0.08	86.71 ± 0.35	88.48 ± 0.35	89.40 ± 0.06
	TL	86.37 ± 0.27	86.46 ± 0.53	88.15 ± 0.35	89.49 ± 0.34	89.64 ± 0.04
SSL	CutMix	87.38 ± 0.24	87.87 ± 0.30	88.63 ± 0.26	89.16 ± 0.29
	ClassMix	87.54 ± 0.22	88.16 ± 0.31	88.68 ± 0.15	89.17 ± 0.20
	MT	87.37 ± 0.51	87.67 ± 0.46	88.78 ± 0.30	89.31 ± 0.21
	MT+CutMix	86.98 ± 0.38	88.33 ± 0.17	88.84 ± 0.37	89.36 ± 0.15
	MT+ClassMix	87.22 ± 0.05	88.08 ± 0.13	88.62 ± 0.10	88.71 ± 0.13
	CPS	88.44 ± 0.11	88.75 ± 0.57	89.17 ± 0.08	89.50 ± 0.07
	CPS+CutMix	88.25 ± 0.28	88.79 ± 0.12	89.14 ± 0.19	89.53 ± 0.33
	ClassHyPer	88.37 ± 0.07	88.98 ± 0.19	89.30 ± 0.16	89.44 ± 0.21

. This dataset can reach nearly 90% $\mathrm{IoU}$, and there is a relatively small standard deviation in multiple repeated experiments between different sub-samplings, representing this dataset’s robustness and high quality. When 5% labeled data (236 labels) are used, the $\mathrm{IoU}$ of TL and ClassHyPer improves from 81.65 to 86.37 and 88.37%, respectively, compared to the baseline. Relatively speaking, CPS-based approaches obtain better performance than others. Impressively, only using 5% labeled data, the CPS-based methods can obtain high accuracy that is close to that achieved by TL with 100% labels. As a result of its intrinsically high labeling accuracy, this dataset is insensitive to the amount of training data. Hence, CutMix and ClassMix achieve similar results, such that we cannot find significant differences between them. Furthermore, when using 4736 labels, the $\mathrm{IoU}$ (89.64%) can outperform some reported methods—e.g., SiU-Net [6] and SRI-Net [60]—exhibiting the availability and effectiveness of our modified FCN model. Likewise, as seen from the visualization results shown in Figure 11, it is difficult to tell the visual differences between these SSL approaches due to their relatively high accuracy.

4.5.4. Potsdam

Unlike the previous three datasets, the Potsdam dataset was created for multiclass semantic segmentation; moreover, it has an extremely high spatial resolution, so the scene complexity is significantly greater than that of previous datasets. We expected to use this dataset to verify the applicability of ClassHyPer on multiclass segmentation. As seen from

Table 5. Accuracy ($\mathrm{IoU}$, %) comparison of different methods on the Potsdam dataset, where the values in bold are the best.

Method		5% (31)	10% (61)	20% (122)	50% (306)	100% (612)
Sup	Baseline	46.63 ± 0.98	50.31 ± 1.91	57.01 ± 0.28	64.34 ± 0.31	68.86 ± 0.12
	TL	63.09 ± 0.85	66.41 ± 0.42	70.23 ± 0.26	71.65 ± 0.33	73.49 ± 0.36
SSL	CutMix	65.45 ± 0.25	67.54 ± 0.80	70.14 ± 0.58	71.51 ± 0.15
	ClassMix	65.62 ± 0.91	67.89 ± 0.55	70.42 ± 0.34	71.73 ± 0.27
	MT	61.84 ± 0.82	63.9 ± 0.73	68.02 ± 0.83	70.61 ± 0.33
	MT+CutMix	61.38 ± 0.79	65.59 ± 0.67	68.49 ± 0.94	71.06 ± 0.31
	MT+ClassMix	64.83 ± 0.72	66.38 ± 0.93	69.11 ± 0.38	70.51 ± 0.26
	CPS	62.72 ± 0.89	65.48 ± 0.23	70.09 ± 0.50	71.05 ± 0.41
	CPS+CutMix	66.27 ± 0.69	68.17 ± 0.55	70.28 ± 0.31	71.75 ± 0.65
	ClassHyPer	67.13 ± 0.40	68.63 ± 0.60	70.54 ± 0.30	71.87 ± 0.23

, ClassHyPer can outperform other perturbation-based approaches in all data proportions. When using 5% labeled data (31 labels), ClassHyPer obtained a considerable improvement in accuracy over TL, increasing from 63.09 to 67.13%. However, SSL approaches do not improve accuracy significantly compared to TL when the proportion of labels increases by over 20%. Furthermore, MT is not helpful to the model performance, whether it is combined with data-level perturbations or not. Figure 12 shows the visualization results based on 5% labels; we can see that it is hard to classify all pixels into six classes, since some categories may possess relatively homogeneous characteristics. For example, distinguishing low vegetation from trees is challenging in practice due to their similar features. However, ClassHyPer can still improve the accuracy and achieve visually smoother predictions.

4.5.5. Vaihingen

Although the Vaihingen dataset also has six classes like the Potsdam dataset, it consists of color-infrared images instead of RGB images, in contrast to the previous four datasets. As shown in

Table 6. Accuracy ($\mathrm{IoU}$, %) comparison of different methods on the Vaihingen dataset, where the values in bold are the best.

Method		5% (34)	10% (69)	20% (138)	50% (346)	100% (692)
Sup	Baseline	44.92 ± 0.86	48.54 ± 0.8	50.15 ± 0.26	55.47 ± 1.03	61.63 ± 0.56
	TL	55.27 ± 0.93	59.28 ± 1.56	60.98 ± 0.91	65.81 ± 0.10	67.39 ± 0.49
SSL	CutMix	58.86 ± 1.71	62.87 ± 1.22	64.61 ± 1.37	65.81 ± 1.59
	ClassMix	60.33 ± 0.83	65.19 ± 1.55	66.39 ± 0.49	66.82 ± 0.65
	MT	59.46 ± 0.87	62.46 ± 1.58	64.85 ± 2.84	66.33 ± 0.40
	MT+CutMix	60.46 ± 1.51	64.85 ± 1.14	65.35 ± 1.27	66.63 ± 1.32
	MT+ClassMix	60.57 ± 1.40	64.21 ± 1.15	65.46 ± 0.70	67.60 ± 0.69
	CPS	62.70 ± 1.26	65.88 ± 1.63	66.98 ± 0.80	67.40 ± 0.85
	CPS+CutMix	63.16 ± 1.46	66.17 ± 0.80	67.00 ± 1.10	67.15 ± 0.99
	ClassHyPer	63.49 ± 1.95	66.31 ± 1.67	67.03 ± 1.18	68.08 ± 0.47

, ClassHyPer can achieve the best accuracy on all data partitions. All SSL approaches can improve the model performance over the baseline with very few labels, proving their applicability on three-band color-infrared images for multiclass semantic segmentation. The most interesting result is that the $\mathrm{IoU}$ of ClassHyPer with 50% labels (68.08%) even outperforms the purely supervised approach with 100% labels (67.39%), revealing the great potential of SSL approaches. The visualization results based on 5% labels (Figure 13) show that the ground-truth label may have some unexpected errors. For example, in Figure 13(a1), the area surrounded by the orange rectangle contains some impervious surface pixels, but we cannot find them from the ground-truth label (b1). Furthermore, the rectangle in Figure 13(a2) shows an area with an impervious surface, while it actually turned out to be low vegetation via manual inspection. For a clearer comparison, Figure 14 provides an enlarged visualization of the area surrounded by the orange rectangle in Figure 13. It is impressive that SSL approaches are able to recognize these areas, which also demonstrates the powerful capability of DL methods and the excellent performance of the SSL paradigm, even with a limited number of labeled training data.

4.6. Overall Comparison between Datasets

4.6.1. Comparison of ClassHyPer with Different Proportions of Labels

To analyze and compare the results of the proposed method between different datasets, we present the accuracy of results using ClassHyPer in

Table 7. Accuracy ($\mathrm{IoU}$, %) comparison of ClassHyPer on different datasets.

Dataset	Training Labels	ClassHyPer				TL with 100% Labels
		5%	10%	20%	50%
DG_Road	3735	57.92 ± 0.26	60.03 ± 0.28	61.14 ± 0.13	63.19 ± 0.27	64.73 ± 0.38
Massa_Building	1065	69.85 ± 0.25	71.62 ± 0.51	72.17 ± 0.47	72.31 ± 0.38	73.15 ± 0.12
WHU_Building	4736	88.37 ± 0.07	88.98 ± 0.19	89.30 ± 0.16	89.44 ± 0.21	89.64 ± 0.04
Potsdam	612	67.13 ± 0.40	68.63 ± 0.60	70.54 ± 0.30	71.87 ± 0.23	73.49 ± 0.36
Vaihingen	692	63.49 ± 1.95	66.31 ± 1.67	67.03 ± 1.18	68.08 ± 0.47	67.39 ± 0.49

.

As shown in Table 1 and Table 7, these five datasets have heterogeneous characteristics in multiple dimensions, such as the number of training labels, spatial resolution, categories, and the best training accuracy. Overall, except for the WHU_Building dataset, the accuracy of the other datasets gradually increased with the growing number of training labels. For example, if treating the accuracy from TL with 100% labels as the upper boundary of accuracy, the $\mathrm{IoU}$ with 50% labels from each dataset is close to the upper boundary. Interestingly, the accuracy of the Vaihingen dataset with 50% labels even outperformed the upper boundary, showing the powerful capability of the proposed approaches. In addition, when only using 5% training labels, ClassHyPer can achieve considerable accuracy against that with 100% labels, as shown in Table 11.

Moreover, we found that different levels of accuracy were achieved on different datasets. Specifically, the WHU_Building dataset had the most labeled training images (4736), and achieved the highest accuracy in all proportions. Through reviewing the WHU_Building data, we can see that it has a very high spatial resolution (0.3 m), enabling it to delineate more accurate building boundaries and have a higher labeling accuracy. The creators of this dataset also highlighted that around six months were taken to create the dataset, and strict manual checking ensured its final labeling accuracy. In addition, the dataset was created for binary classification, reducing its task complexity and enabling relatively high accuracy.

Although the DG_Road dataset used 3735 labels for training, its accuracy was the lowest amongst all datasets in every proportion. There are two possible explanations for this: (1) its labeling accuracy is limited by its relatively lower spatial resolution and heterogeneous imaging quality. For instance, as this dataset consists of images from multiple satellites with different characteristics, it is hard to label some specific regions even for humans. (2) The issue of class imbalance is severe in this dataset, which significantly affects the final model performance. For example, the road pixels in this dataset only account for 4.21% of all training labels, as shown in

Table 8. Statistics of pixels in different categories of each dataset based on ground-truth data.

Dataset	Classes	Train		Val		Test
		Ratio	Pixels	Ratio	Pixels	Ratio	Pixels
DG_Road	Background	95.79%	937,917,468	95.62%	156,165,832	95.75%	468,869,474
	Road	4.21%	41,190,372	4.38%	7,149,880	4.25%	20,815,518
Massa_Building	Background	84.47%	235,820,198	87.39%	8,246,907	78.84%	18,601,348
	Building	15.53%	43,363,162	12.61%	1,190,277	21.16%	4,991,612
WHU_Building	Background	81.34%	1,009,799,430	89.00%	241,707,225	88.87%	562,861,562
	Building	18.66%	231,714,558	11.00%	29,873,959	11.13%	70,478,342
Potsdam	Impervious surfaces	28.85%	46,203,252	27.54%	18,265,098	31.47%	41,579,812
	Buildings	26.17%	41,919,727	28.05%	18,604,168	23.92%	31,601,996
	Low vegetation	23.52%	37,670,506	23.58%	15,637,762	21.01%	27,757,373
	Trees	15.08%	24,153,823	13.52%	8,969,936	17.04%	22,515,491
	Cars	1.69%	2,710,112	1.68%	1,116,603	1.97%	2,596,193
	Clutter/Background	4.69%	7,512,564	5.62%	3,728,865	4.59%	6,069,711
Vaihingen	Impervious surfaces	29.34%	53,219,815	26.48%	4,719,397	27.35%	17,853,972
	Buildings	26.88%	48,763,596	24.24%	4,321,511	26.49%	17,289,928
	Low vegetation	19.56%	35,478,641	21.93%	3,909,070	20.25%	13,219,923
	Trees	22.08%	40,052,822	26.04%	4,641,147	23.63%	15,421,237
	Cars	1.26%	2,283,335	1.23%	219,078	1.31%	855,221
	Clutter/Background	0.89%	1,605,439	0.09%	15,589	0.97%	633,575

.

The building labels in the Massa_Building dataset are directly referenced from the OpenStreetMap database without manual correction, which involves many unexpected errors. At the same time, its ratio of building pixels (15.53%) is greater than that of road pixels in the DG_Road dataset. Hence, we can obtain an accuracy that occupies a middle ground between the WHU_Building and DG_Road datasets.

Both the Potsdam and Vaihingen datasets possess extremely high spatial resolution, thus containing more details and noise information. The multiclass classification task is more difficult due to severe unbalanced class issues among the different categories. As Table 8 shows, both datasets have a limited number of car pixels, which only account for 1.69 and 1.26% of all training pixels, respectively, making it hard to classify such a rare category. Furthermore, as we mentioned previously, the more classes, the greater chance that different categories will possess similar characteristics. For instance, it is challenging to distinguish low vegetation from trees due to their similar spectral characteristics, even with many training samples. Therefore, the accuracy of these two datasets on all proportions only ranges from 63 to 73%, although the accuracy of Potsdam is higher than that of Vaihingen.

4.6.2. Comparison of Different Approaches with 5% Labels

Additionally, in order to further compare the abovementioned approaches with a limited number of labels, we summarized the accuracy results of all five datasets based on 5% labels, as shown in

Table 9. Accuracy comparison ($\mathrm{IoU}$, %) on different datasets with 5% labels, where the values in bold are the best for each dataset.

Dataset	Method
	CutMix	ClassMix	MT	MT+CutMix	MT+ClassMix	CPS	CPS+CutMix	ClassHyPer
DG_Road	55.63 ± 0.33	55.06 ± 0.49	51.70 ± 0.87	55.85 ± 0.47	54.23 ± 0.60	52.10 ± 1.16	58.88 ± 0.46	57.92 ± 0.26
Massa_Building	66.32 ± 1.49	68.98 ± 0.40	63.27 ± 2.36	66.54 ± 1.52	67.98 ± 1.38	66.75 ± 0.64	69.03 ± 1.26	69.85 ± 0.25
WHU_Building	87.38 ± 0.24	87.54 ± 0.22	87.37 ± 0.51	86.98 ± 0.38	87.22 ± 0.05	88.44 ± 0.11	88.25 ± 0.28	88.37 ± 0.07
Potsdam	65.45 ± 0.25	65.62 ± 0.91	61.84 ± 0.82	61.38 ± 0.79	64.83 ± 0.72	62.72 ± 0.89	66.27 ± 0.69	67.13 ± 0.40
Vaihingen	58.86 ± 1.71	60.33 ± 0.83	59.46 ± 0.87	60.46 ± 1.51	60.57 ± 1.40	62.70 ± 0.26	63.16 ± 1.46	63.49 ± 1.95

. Based on the results, it is clear that data-level perturbation methods (i.e., CutMix and ClassMix) can obtain greater accuracy improvements than model-level perturbation methods (i.e., MT and CPS). For the data-level perturbation methods, ClassMix outperformed CutMix on all datasets except for DG_Road, which proves the applicability of ClassMix in building extraction and land cover classification other than road extraction. For the model-level perturbation methods, CPS was superior to MT on all datasets. Although some studies [31,32] still employed MT in their methods, CPS has become a novel and competitive SSL paradigm from the perspective of model perturbation. In fact, the success of CPS can be attributed not only to its increased number of training parameters, but also to the multi-model ensembling strategy by encouraging mutual supervision. Regarding the hybrid pipeline, the performance of MT-based approaches cannot compete with CPS-based methods. Specifically, the CPS-based hybrid schemes can yield the best performance on all datasets, of which ClassHyPer achieved the best accuracy on three datasets, while CPS+CutMix also possessed a comparable level of accuracy.

Through the overall comparison between five datasets involving different tasks and characteristics, ClassHyPer is capable of being applied to scenarios with very few labeled training data. Moreover, the hybrid perturbation methods based on consistency regularization integrating CPS and mask-based data augmentation can achieve relatively high accuracy. We should choose the proper approach based on corresponding data and their characteristics in specific applications. Regardless, the use of unlabeled data can be more cost-effective in the case of a limited number of labels.

5. Discussion

This section further analyzes and discusses the experimental results involving the time efficiency of the proposed approaches and the label redundancy in training.

5.1. Time Efficiency

To analyze the time efficiency of the proposed approach, we chose two large datasets (DG_Road and WHU_Building). These two datasets contain more than 3700 labeled data for training, and they can be good representatives of time consumption with SSL methods when using a large number of unlabeled data.

As shown in

Table 10. Time efficiency analysis.

Dataset		TL		ClassHyPer
		Time (h)	$IoU(\%)$	Time (h)	$IoU(\%)$
DG_Road	5% (186)	0.37	52.88 ± 0.39	5.20	57.92 ± 0.26
	10% (373)	0.47	56.76 ± 0.11	5.12	60.03 ± 0.28
	20% (747)	0.63	59.34 ± 0.25	5.24	61.14 ± 0.13
	50% (1867)	1.17	62.49 ± 0.21	5.44	62.56 ± 0.09
	100% (3735)	2.00	64.73 ± 0.38
WHU_Building	5% (236)	0.42	86.37 ± 0.27	6.64	88.37 ± 0.07
	10% (473)	0.52	86.46 ± 0.53	6.53	88.98 ± 0.19
	20% (947)	0.73	88.15 ± 0.35	6.76	89.30 ± 0.16
	50% (2368)	1.45	89.49 ± 0.34	7.01	89.44 ± 0.21
	100% (4736)	2.62	89.64 ± 0.04

, for the DG_Road dataset, when we used 5% labeled data for training, TL took 0.37 h to achieve 52.88% $\mathrm{IoU}$, while ClassHyPer obtained 57.92% $\mathrm{IoU}$ in 5.2 h. The TL method is evidently more efficient in terms of time; however, in order to reach the same accuracy level as ClassHyPer with 5% labels, ~10% more labeled data are required in TL. In fact, creating 10% more labels (~370 labels) in this dataset will take much more time than 5 h based on our usual experiences. The same applies to the WHU_Building dataset; although ClassHyPer took more time (6.64 h) for training, it could obtain higher accuracy with fewer labels, thus saving more time for labeling work. Moreover, we found that the accuracy on the WHU_Building dataset was not significantly improved when increasing the proportion of labeled data from 5 to 10%. This is probably because the high quality of the dataset makes the accuracy insensitive to small increases in label size.

When analyzing time efficiency, we found that ClassHyPer takes a longer time for training. However, it can learn from large amounts of unlabeled data and significantly improve the segmentation accuracy. Particularly, when only a limited number of labeled data are at hand, this approach can accelerate problem solving.

5.2. Label Redundency

The proposed approach demonstrated high accuracy in the case of very few labels based on the above analysis. In the meantime, we found that training accuracy did not improve linearly with the growing number of labeled data. If the result of using 100% labeled data for fully supervised learning with TL is taken as the upper boundary of accuracy, we can calculate the ratio of $\mathrm{IoU}$ from ClassHyPer (SSL $\mathrm{IoU}$) to the upper boundary $\mathrm{IoU}$ (Sup $\mathrm{IoU}$).

Table 11. The ratio of $\mathrm{IoU}$ from ClassHyPer with different proportions of labeled training data to $\mathrm{IoU}$ from TL with 100% labels.

Dataset	5%		10%		20%		50%		100%
	Labels	$\frac{SSL IoU}{Sup IoU}$	Labels	$\frac{SSL IoU}{Sup IoU}$	Labels	$\frac{SSL IoU}{Sup IoU}$	Labels	$\frac{SSL IoU}{Sup IoU}$	Labels
DG_Road	186	89.48%	373	92.74%	747	94.45%	1867	96.65%	3735
Massa_Building	53	95.49%	106	97.91%	212	98.66%	532	98.85%	1065
WHU_Building	236	98.58%	473	99.26%	947	99.62%	2368	99.78%	4736
Potsdam	30	91.34%	61	93.38%	122	95.98%	306	97.80%	612
Vaihingen	34	94.21%	69	98.40%	138	99.47%	346	101.02%	692

shows the comparison results across all datasets. It is worth noting that the ratio of accuracy obtained by ClassHyPer with 5% labels to that obtained by a purely supervised method with 100% labels was more than 89%. On the one hand, this statistic emphasizes how the proposed approach can significantly enhance the capability of the DL model by leveraging a mass of unlabeled data, which is encouraging for the application of SSL in remote sensing applications. On the other hand, the accuracy is only improved by less than 10% based on the remaining 95% of labeled data, which means that there are many redundant labels in the training data. For example, a 98.58% ratio of $\mathrm{IoU}$ was reached on the WHU_Building dataset with just 5% labels, which is extremely close to the upper boundary of accuracy. Furthermore, we also observed that a few unexpected errors exist in the labels, which might be another factor affecting the final accuracy. Therefore, improving the model performance with few but effective labels is an interesting topic worth studying in the future.

6. Conclusions

In this study, aiming at alleviating the label scarcity problem in remote sensing semantic segmentation applications, we comprehensively analyzed several advanced SSL methods based on consistency regularization from the perspective of data- and model-level perturbation. Then, an end-to-end ClassMix-based hybrid perturbation SSL approach—i.e., ClassHyPer—was introduced to improve the model’s capability when faced with a limited number of annotations. The experimental results on five datasets demonstrated that the proposed approach is able to achieve the best performance on three of them by incorporating 5% labeled data and the remaining 95% unlabeled data; at the same time, comparatively high accuracy was obtained on the other two datasets. Moreover, such a method does not require the setting of a confidence threshold, and can be easily paired with existing DL models. Although more time is required for training, the model can save time spent on labeling work.

Through various experiments, we noted that there are many redundant labels in training. Therefore, we will further explore how to reduce label redundancy and improve the effectiveness of labeling work, e.g., by incorporating an active learning scheme. In addition, we only conducted experiments on remote sensing imagery with three bands (R-G-B or IR-R-G), so more studies on multispectral imagery (over three bands) are still required in the future. To this end, the traditional parameter transfer learning pipeline used in this study needs to be adapted accordingly for the multispectral images of more than three bands. Furthermore, this method can be extended to specific remote sensing applications—such as disaster and agriculture monitoring—to exploit its huge potential in practice.