A Multi-Stage Vessel Tracklet Association Method for Compact High-Frequency Surface Wave Radar
Abstract
:1. Introduction
2. Preliminaries
2.1. Tracklet Representation
2.2. Average Heading and Average Speed Calculation
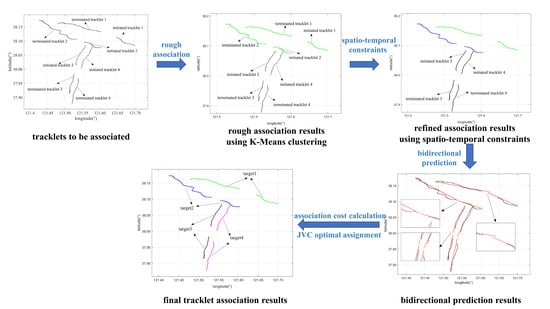
3. A Multi-Stage Tracklet Association Method
3.1. Rough Tracklet Association Based on K-Means Clustering
| Algorithm 1 Rough tracklet association using k-means clustering |
|
3.2. Tracklet Pair Set Refinement by Spatiotemporal Constraints
3.3. Optimal Tracklet Assignment Based on a Bidirectional Prediction
3.3.1. Tracklet Association Cost Calculation
3.3.2. Optimal Tracklet Assignment
4. Experiment Results
4.1. Experiments with Simulated Data
4.2. Experiments with Field Data
4.2.1. Analysis of Track Fragmentation Cause
4.2.2. Analysis of Tracklet Association Results
4.2.3. Analysis of Association Accuracy and Computational Complexity
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HFSWR | high-frequency surface wave radar |
| CORMS | compact over-the-horizon radar for maritime surveillance |
| CIT | coherent integration time |
| TSA | track segment association |
| JVC | Jonker–Volgenant–Castanon |
| FMICW | frequency modulated interrupted continuous wave |
| CFAR | constant false alarm rate |
| DOA | direction of arrival |
| MUSIC | multiple signal classification |
| DBF | digital beamforming |
| CMKF | converted measurement Kalman filter |
| SNR | signal-to-noise ratio |
| SCR | signal-to-clutter ratio |
| AIS | automatic identification system |
References
- Sun, W.; Pang, Z.; Huang, W.; Ji, Y.; Dai, Y. Vessel velocity estimation and tracking from Doppler echoes of T/R-R composite compact HFSWR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4427–4440. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, J.; Wang, Y.; Sun, W.; Li, M. Target monitoring using small-aperture compact high-frequency surface wave radar. IEEE Aerosp. Electron. Syst. Mag. 2018, 33, 22–31. [Google Scholar] [CrossRef]
- Park, S.; Cho, C.J.; Ku, B.; Lee, S.; Ko, H. Compact HF surface wave radar data generating simulator for ship detection and tracking. IEEE Geosci. Remote Sens. Lett. 2017, 14, 969–973. [Google Scholar] [CrossRef]
- Roarty, H.J.; Rivera Lemus, E.; Handel, E.; Glenn, S.M.; Barrick, D.E.; Isaacson, J. Performance evaluation of SeaSonde high-frequency radar for vessel detection. Mar. Technol. Soc. J. 2011, 45, 14–24. [Google Scholar] [CrossRef]
- Smith, M.; Roarty, H.; Glenn, S.; Whelan, C.; Barrick, D.; Isaacson, J. Methods of associating CODAR SeaSonde vessel detection data into unique tracks. In Proceedings of the 2013 OCEANS, San Diego, CA, USA, 23–27 September 2013; pp. 1–5. [Google Scholar]
- Lu, B.; Wen, B.Y.; Tian, Y.W.; Wang, R.K. A vessel detection method using compact-array HF radar. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2017–2021. [Google Scholar] [CrossRef]
- Zhou, H.; Roarty, H.; Wen, B.Y. Wave extraction with portable high-frequency surface wave radar OSMAR-S. Ocean Univ. China 2014, 13, 957–963. [Google Scholar] [CrossRef]
- Helzel, T.; Hansen, B.; Kniephphoff, M.; Petersen, L.; Valentin, M. Introduction of the compact HF radar WERA-S. In Proceedings of the IEEE/OES Baltic International Symposium, Klaipeda, Lithuania, 8–10 May 2012; pp. 1–3. [Google Scholar]
- Roarty, H.J.; Barrick, D.E.; Kohut, J.T.; Glenn, S.M. Dual-use of compact HF radars for the detection of mid- and large-size vessels. Turk. J. Electr. Eng. Comput. Sci. 2010, 18, 373–388. [Google Scholar]
- Sun, W.; Huang, W.; Ji, Y.; Dai, Y.; Ren, P.; Zhou, P.; Hao, X. A vessel azimuth and course joint re-estimation method for compact HFSWR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1041–1051. [Google Scholar] [CrossRef]
- Sun, W.; Huang, W.; Ji, Y.; Dai, Y.; Ren, P.; Zhou, P. Vessel tracking with small-aperture compact high-frequency surface wave radar. In Proceedings of the MTS/IEEE Oceans, Marseille, France, 17–20 June 2019; pp. 1–4. [Google Scholar]
- Yeom, S.W.; Kirubarajan, T.; Bar-Shalom, Y. Track segment association, fine-step IMM and initialization with Doppler for improved track performance. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 293–309. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Kirubarajan, T.; Gokberk, C. Tracking with classification-aided multiframe data association. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 868–878. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part I. Dynamic models. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1364. [Google Scholar]
- Zhang, S.; Bar-Shalom, Y. Track segment association for GMTI tracks of evasive move-stop-move maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1899–1914. [Google Scholar] [CrossRef]
- Pan, S.S.; Bao, Q.L.; Hou, W.B.; Che, Z.P. An improved track segment association algorithm using MM-GNN method. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium Spring—(PIERS), St. Petersburg, Russia, 22–25 May 2017; pp. 675–681. [Google Scholar]
- Raghu, J.; Srihari, P.; Tharmarasa, R.; Kirubarajan, T. Comprehensive track segment association for improved track continuity. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2463–2480. [Google Scholar] [CrossRef]
- Hong, S.X.; Peng, D.L.; Shi, Y.F. Track-to-track association using fuzzy membership function and clustering for distributed information fusion. In Proceedings of the 37th Chinese Control Conference, Wuhan, China, 25–27 July 2018; pp. 4028–4032. [Google Scholar]
- Zhu, Y.Q.; Zhou, S.L.; Gao, G.; Ji, K.F. Emitter Target Tracking by Tracklet Association Using Affinity Propagation. IEEE Sens. J. 2015, 15, 5645–5653. [Google Scholar] [CrossRef]
- Shao, H.; Japkowicz, N.; Abielmona, R.S. Vessel track correlation and association using fuzzy logic and Echo State Networks. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 2322–2329. [Google Scholar]
- Zhang, L.; Mao, D.W.; Niu, J.; Wu, J.; Ji, Y.G. Continuous Tracking of Targets for Stereoscopic HFSWR Based on IMM Filtering Combined with ELM. Remote Sens. 2020, 12, 272. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Ji, M.; Huang, W.; Ji, Y.; Dai, Y. Vessel tracking using bistatic compact HFSWR. Remote Sens. 2020, 12, 1266. [Google Scholar] [CrossRef] [Green Version]
- Bar-Shalom, Y.; Willett, P.; Tian, X. Tracking and Data Fusion: A Handbook of Algorithms; YBS Publishing: Storrs, CT, USA, 2011. [Google Scholar]
- Nikolic, D.; Stojkovic, N.; Lekic, N. Maritime over the horizon sensor integration: High frequency surface-wave-radar and automatic identification system data integration algorithm. Sensors 2018, 18, 1147. [Google Scholar] [CrossRef] [Green Version]
- Xiao, J.Z.; Li, X. A Research of the Partition Clustering Algorithm. In Proceedings of the 2010 International Symposium on Intelligence Information Processing and Trusted Computing, Huanggang, China, 28–29 October 2010; pp. 551–553. [Google Scholar]
- Jonker, R.; Volgenant, A. A shortest augmenting path algorithm for dense and sparse linear assignment problems. Computing 1987, 38, 325–340. [Google Scholar] [CrossRef]
- Kadar, I.; Eadan, E.R.; Gassner, R.R. Comparison of robustized assignment algorithms. In Proceedings of the Aerospace Defence Sensing and Control (Aero Sense) Conference, Orlando, FL, USA, 21–25 April 1997; Volume 3068, pp. 240–249. [Google Scholar]
- Bordonaro, S.; Willett, P.; Bar-Shalom, Y. Decorrelated unbiased converted measurement Kalman filter. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1431–1444. [Google Scholar] [CrossRef]










| Initial Range (km) | Initial Azimuth () | Initial Doppler Velocity (km/h) | |
|---|---|---|---|
| Target 1 | 107 | −10 | 22 |
| Target 2 | 106 | −11 | 21 |
| Target 3 | 74 | −7 | −19 |
| Target 4 | 112 | −8 | −23 |
| Target 5 | 93 | −7 | −19 |
| Terminated Tracklet | Terminated Tracklet 1 | Terminated Tracklet 2 | |
|---|---|---|---|
| Initiated Tracklet | |||
| Initiated Tracklet 1 | 0.1117 | 0.0228 | |
| Initiated Tracklet 2 | 0.7020 | 0.5933 | |
| Terminated Tracklet | Terminated Tracklet 3 | Terminated Tracklet 4 | |
|---|---|---|---|
| Initiated Tracklet | |||
| Initiated Tracklet 3 | 0.6052 | 0.1577 | |
| Initiated Tracklet 4 | 0.7173 | 0.1124 | |
| (%) | (%) | (%) | Average Running Time (s) | |
|---|---|---|---|---|
| TSA method in [12] | 63.4 | 19.5 | 17.1 | 10.4 |
| Proposed Method | 93.5 | 4.3 | 2.2 | 3.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Pang, Z.; Huang, W.; Ma, P.; Ji, Y.; Dai, Y.; Li, X. A Multi-Stage Vessel Tracklet Association Method for Compact High-Frequency Surface Wave Radar. Remote Sens. 2022, 14, 1601. https://doi.org/10.3390/rs14071601
Sun W, Pang Z, Huang W, Ma P, Ji Y, Dai Y, Li X. A Multi-Stage Vessel Tracklet Association Method for Compact High-Frequency Surface Wave Radar. Remote Sensing. 2022; 14(7):1601. https://doi.org/10.3390/rs14071601
Chicago/Turabian StyleSun, Weifeng, Zhenzhen Pang, Weimin Huang, Peng Ma, Yonggang Ji, Yongshou Dai, and Xiaotong Li. 2022. "A Multi-Stage Vessel Tracklet Association Method for Compact High-Frequency Surface Wave Radar" Remote Sensing 14, no. 7: 1601. https://doi.org/10.3390/rs14071601
APA StyleSun, W., Pang, Z., Huang, W., Ma, P., Ji, Y., Dai, Y., & Li, X. (2022). A Multi-Stage Vessel Tracklet Association Method for Compact High-Frequency Surface Wave Radar. Remote Sensing, 14(7), 1601. https://doi.org/10.3390/rs14071601