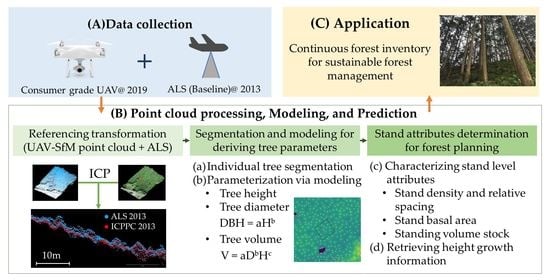
Integrating UAV-SfM and Airborne Lidar Point Cloud Data to Plantation Forest Feature Extraction

Abstract

A low-cost but accurate remote-sensing-based forest-monitoring tool is necessary for regularly inventorying tree-level parameters and stand-level attributes to achieve sustainable management of timber production forests. Lidar technology is precise for multi-temporal data collection but expensive. A low-cost UAV-based optical sensing method is an economical and flexible alternative for collecting high-resolution images for generating point cloud data and orthophotos for mapping but lacks height accuracy. This study proposes a protocol of integrating a UAV equipped without an RTK instrument and airborne lidar sensors (ALS) for characterizing tree parameters and stand attributes for use in plantation forest management. The proposed method primarily relies on the ALS-based digital elevation model data (ALS-DEM), UAV-based structure-from-motion technique generated digital surface model data (UAV-SfM-DSM), and their derivative canopy height model data (UAV-SfM-CHM). Following traditional forest inventory approaches, a few middle-aged and mature stands of Hinoki cypress (Chamaecyparis obtusa) plantation forests were used to investigate the performance of characterizing forest parameters via the canopy height model. Results show that the proposed method can improve UAV-SfM point cloud referencing transformation accuracy. With the derived CHM data, this method can estimate tree height with an RMSE ranging from 0.43 m to 1.65 m, equivalent to a PRMSE of 2.40–7.84%. The tree height estimates between UAV-based and ALS-based approaches are highly correlated (R² = 0.98, p < 0.0001), similarly, the height annual growth rate (HAGR) is also significantly correlated (R² = 0.78, p < 0.0001). The percentage HAGR of Hinoki trees behaves as an exponential decay function of the tree height over an 8-year management period. The stand-level parameters stand density, stand volume stocks, stand basal area, and relative spacing are with an error rate of less than 20% for both UAV-based and ALS-based approaches. Intensive management with regular thinning helps the plantation forests retain a clear crown shape feature, therefore, benefitting tree segmentation for deriving tree parameters and stand attributes.

1. Introduction

Forest ecosystems contain valuable resources and provide various biological, environmental, and economic values. Timber production is still a significant supply need even in the new era of greening the Earth. The forest management process for timber production is a cycle of management practices, including forest regeneration, tending, and harvesting, and utilizes detailed procedures of a silvicultural system. Continuous and multiple processes of forest practices underpin the sustainability of timber production and forest ecosystem development. Precise information on volumetric parameters and even the competitive and health status of individual trees should be geospatially explicit to enable the managers to identify their location and volume in order to facilitate appropriate practices. A tree-level forest database with sufficient and precise data can derive detailed information to support the managers in generating appropriate management plans and thus help achieve sustainability goals. Forest practices such as thinning or selection logging may change forest structure and forest aesthetics, further affecting visitors’ experience in a recreational forest. Appropriate design of logging practices is therefore very critical to retain scenic beauty.

Pilot research [1] highlighted a precision forestry approach that integrates locations and parameters of trees and a three-dimensional scenic beauty evaluation approach to generate selection-logging scenarios for recreational forest management. The impact of various thinning plans on forest scenic beauty was evaluated in advance via a digital-forest-based public-participants geographic information system (PPGIS). Some research recently proposed smart forestry [2,3], emphasizing that forest management should balance forest protection and timber production [4]. In remote sensing, approaches should involve collecting accurate volumetric parameters of individual trees and stand structure attributes to enable better forest management decisions [5,6] to meet the need for multifunctionality.

During recent decades, a variety of remote sensing techniques using high-resolution spaceborne and airborne optical images and airborne laser scanner (ALS) data have been developed for segmenting and classifying tree crowns [7,8,9,10,11], deriving tree height and diameter for volume/biomass estimation [12,13,14,15,16], and determining the dynamic change of tree/stand properties [17,18]. The techniques of watershed segmentation [19], region-growing approach [20], multi-level morphological active contour (MMAC) algorithm [9], multilevel slicing and coding (MSAC) algorithm [21], k-mean clustering [22], and height-scaled crown openness index (HSCOI) [23] have demonstrated their potential in tree-crown delineation and tree parameters extraction using ALS data. The works of [24,25,26] also showed the possibility of generating a tree-level canopy height model of forest stands from unmanned-aerial-vehicle (UAV) point cloud data. The integration of UAV and ALS point cloud data has also been demonstrated as valuable in estimating plot-level parameters of secondary forests [27] and rapidly assessing snow cover and depth changes over forest areas [28].

Chamaecyparis obtuse (the Hinoki cypress, simply Hinoki hereafter) is a major species of plantation forest for timber production in Japan. According to an official record [29], the natural and planted Hinoki forests occupy 2.6 million hectares, accounting for 25% of the forest areas in Japan. During the last decades, Hinoki forests have generally been established/regenerated with a density of around 3000 to 5000 trees per hectare. Before timber harvesting at the rotation age, a series of tending practices with diverse thinning intensity are carried out over the growth period to gradually reduce the stand density and release growth space enabling quantitative and qualitative increments of the trees. However, timber management practices are labor/energy intensive. Repeated management activities significantly increase labor costs and decrease returns due to low economic compensation received through pre-commercial/commercial thinning [30]. This is evident in the case of no increment in log price at harvesting time. Landowners, therefore, tend to be discouraged from constantly managing forests; consequently, increasing return to natural resource production scales has become a significant concern in private forest sectors. Construction of reliable tree-level information with easier but also accurate and lower cost methods is of particular significance for economic forest management. It would improve the cost–benefit ratio and further optimize the supply chain management of timber production.

However, the ALS approach is too expensive for practical forest management, particularly for small-scale private enterprises collecting multi-temporal datasets for frequently deriving canopy height models and their changes over time. Although UAV-based lidar systems can provide very accurate point cloud data, the acquisition cost of the enterprise-grade system or frequent data-collection service charges remains a substantial financial burden for private small-scale forest managers. Achieving continuous forest inventory, periodical ALS data collections at 5-year intervals on an ongoing basis throughout a management period of timber production forest would require a significant financial investment. Consumer-grade UAV-based photogrammetry techniques can provide an alternative option due to low operation time and cost flexibility in collecting multi-temporal and very-high-resolution images for retrieving volumetric information. The use of UAV photogrammetry can generate good-quality ground surface data in open land or sparse forestland [31,32]. However, unlike the excellent penetration ability of laser pulses, its ability to regenerate ground surface in dense forests is extremely limited. Taking advantage of both ALS-based and UAV-based remote sensing approaches, changes in tree parameters are most likely retrievable from UAV-based digital-surface-model (DSM) data and ALS-based digital-elevation-model (DEM) data.

High-quality timber production is the primary goal of plantation forest management. Trees are managed for a long rotation period. An appropriate plan prescribing intensive management practices to control stand density and tree growth is the key to achieving the production goal and even sustainability. Constantly gathering sufficient forest information is particularly important for making plans regarding harvesting, regeneration, and thinning to produce high-quality and valuable trees. Mature plantation forests were planted during an era that lacked high-performance remote sensing technology and now occupy a huge area of land. Although high-resolution remote sensing technology has been widely applied to forest management, research exploring the use of consumer-grade remote sensing tools for high-forest management is rare. Therefore, the objective of this study was to propose a protocol of integrating both ALS and UAV point cloud data for extracting tree-level volumetric parameters of commercially managed forests. The results determining trees’ total height, diameter, stem volume, and derivatives such as stand density and standing timber stocks were examined based on in situ inventory data. Finally, the possibility of retrieving tree height and growth rate via integrating single-temporal ALS reference data and multi-temporal UAV RGB inventory data for forest management is concluded.

2. Materials and Methods

2.1. Study Site

The forest in Japan is distributed over a wide range of land. The forested area accounts for 70% of the country’s land, of which 40% are plantation forests, and 60% are natural forests. Most of the plantation forests planted after 1946 are matured and harvestable for timber production. As mentioned above, Hinoki is one of the most popular species of plantation forests. Two stands of Hinoki forests in the Kameyama area and the Owase area of Mie prefecture, the center of Japan, were selected as the study sites (Figure 1). The Kameyama stand is located at 34.50°N and 136.20°E, with elevation varying between 190 m and 250 m above sea level, and the slope averaged at 12.57 ± 4.64 degrees or 22.63 ± 8.12 percent. The Owase stand is located at 34.00°N and 130.23°E with an elevation from 350 m to 430 m and an average gradient of 34.83 ± 6.76 degrees or 69.58 ± 11.85 percent. The age of the forest at the Kameyama and Owase sites was 46 and 65 years old, respectively, when the inventory [33] was carried out in 2019 and 2018, respectively (

Table 1. Summary of data collection with ALS, UAV, and in situ inventory.

Site	In Situ Inventory Date	UAV Acquisition Date	Stand Age in 2019	ALS Acquisition Date	Stand Age in 2013
Kameyama	26 July 2019	26 July 2019	46	24 November 2013	40
Owase	14 September 2018	14 September 2018	65	27 September 2013	60

). The in situ inventory tree parameters and aggregated stand attributes are used for accuracy assessment. For details of the volumetric determination please refer to Section 2.3.

Table 2. Summary of the descriptive statistics of tree parameters for Kameyama and Owase stands.

Site	Kameyama			Owase
Parameter ¶	DBH (cm)	H (m)	V (m3)	DBH (cm)	H (m)	V (m3)
Minimum	20.50	17.30	0.2954	25.80	16.90	0.5651
Maximum	30.60	19.10	0.6303	40.80	24.10	1.4265
Mean	24.49	18.06	0.4287	32.09	21.04	0.8446
Standard deviation	2.61	0.53	0.0836	4.07	1.72	0.2464

^¶ Parameters DBH, H, and V stand for the diameter at breast height, total height, and volume of trees, respectively.

lists the inventory tree parameters of both the Kameyama forest and the Owase forest at the inventory year. The Owase forest was harvested after the list was made. In contrast to the rotation age, 65 years, of the Hinoki timber production forests, the Owase stand is a mature forest. The Kameyama stand is of commercial-thinning-stand age and is, therefore, a middle-aged forest.

2.2. Airborne Lidar Data and UAV Data Collection and Processing

2.2.1. ALS Data

The Etsumi Sankei Sabo Office of the Ministry of Land, Infrastructure, and Transport (MLIT) supported the ALS data used in this study. The lidar data of the Kameyama forest and the Owase forest was acquired on 24 November 2013, and 27 September 2013, respectively, using a small-footprint multi-return lidar system (Leica Geosystems ALS70, Heerbrugg, Switzerland) mounted on a Cessna Type 208 Aircraft by Kokusai Kogyo Co., Ltd. The flight altitude was around 1828–1981 m above the ground surface. The system has an inertial position and attitude system (IPAS20) providing accurate position and attitude information using a GNSS receiver, a high-accuracy IMU, and an integral processor. It can achieve a positional accuracy of +/−15 cm RMS after post-processing. Based on the evaluation of 212 ground control points (GCPs) that are evenly distributed over the project areas, the official report of Kokusai Kogyo “Etsumisankei Aerial Laser Scanning Project Report” stated that the ALS point cloud data had an error ranging from −0.114 m to 0.117 m; the averaged slant distance RMSE was 0.051 m, and standard deviation of horizontal and vertical errors was 0.027 m and 0.047 m, respectively [34]. The lidar dataset with canopy/ground pulse return densities of 21.6/1.2 and 23.4/4.3 points per square meter was used to produce DEM, DSM, and canopy height model (CHM) images. An additional ALS data that covered the Kameyama forest was acquired on 19 September 2020, using the Orion M300 lidar survey system mounted on a Cessna 208B Aircraft by Aero Asahi Corporation. The flight altitude was 2000 m above the ground surface. The canopy/ground point cloud data have a density of 16.4/2.5 points per square meter and the positional error ranged from −0.057 m to 0.058 m and RMSE was 0.042 m [35]. This dataset was used to evaluate the height growth rate of trees through the integration of the 2013 ALS dataset.

Based on the point cloud density of the study sites, the practical pixel size in the rasterized image [9] was around 0.21–0.25 m for the canopy data and 0.48–0.91 m for the ground data. In other words, the best resolution for a raster image was around 0.25 m and 0.91 m for presenting the canopy surface and ground surface models. To retrieve the crown size of every single tree of the study sites, we tried to retain the performance of the high canopy point cloud of the ALS data and generated a 0.25 m pixel size of the DSM image (DSM_ALS). However, the generated DEM image originally had a pixel size of 1.0 m and was then resampled to 0.25 m/pixel (DEM_ALS) for deriving the CHM_ALS.

2.2.2. UAV Data

The UAV data of the Kameyama forest and Owase forest were acquired in September 2018 and July 2019 using a UAV of DJI Phantom4 Pro carrying a 1 in, 20 megapixels sensor. This platform is a consumer-grade and low-cost machine equipped with a GNSS unit for receiving the GPS and GLONASS signals but without a real-time-kinematics (RTK) facility for geolocating coordinates. The UAV flight mission was implemented via a Litchi (VC-Technology, London, UK) UAV auto control system with parameter settings 100–150 m above the land for the flight height, and 90% and 80% for the end lap and side lap of the photographs. The raw RGB images had a resolution of 0.03 m. The difference in data acquisition time between the ALS and UAV data provides the length of a growth period to determine volumetric parameters of both individual trees and stands of the Hinoki forests.

UAV-SfM Raw Point Cloud Generation

A technique integrating the structure-from-motion (SfM) and multi-view stereo (MVS) mounted in Agisoft Metashape 1.7.6 was applied to generate 2D orthophotos and 3D point cloud data from the aerial photographs of the study sites [36,37,38]. The SfM-MVS technique has built onto traditional stereoscopic methods due to advances in computer vision algorithms, such as the scale invariance feature transform (SIFT) [39] and parallel bundle adjustments on graphic processing units [24,36]. It can supply 3D point cloud data with geographic coordinates.

In general, a UAV is equipped with a GNSS unit which records the geolocation of the image center and exports the exchangeable image file format (EXIF) information to photos, allowing the SfM technique to generate accurate point cloud data for further applications. However, it is highly probable the point cloud data generated via the images of a UAV equipped without an RTK-based positioning system (hereafter UAV-SfM) will have significant locational errors and therefore introduce substantial bias to tree height determination. Therefore, post-processing of georeferencing to the raw point cloud data is mandated for deriving volumetric parameters of forest stands. Using extra GCP coordinates collected via high-performance GNSS systems on the ground [24,25] can help to upgrade the geolocation accuracy. However, given the condition of high canopy closure in Kameyama and Owase forests, it is highly probable that the GNSS signal will be affected by the dense canopy. In fact, mature plantation forest generally has a dense canopy. Thus, the proposed algorithm is based on GCP-free consideration. The UAV-SfM point cloud data used for deriving tree parameters and stand attributes is the final product whose accuracy has been evaluated using artificial-object-based checking points that are visually identifiable on the ground and the orthoimage.

UAV-SfM and ALS Point Cloud Referencing Transformation

According to [40], two range images or datasets with the feature of the same reality acquired from different views can be registered together with a performance of the minimized registration error by the iterative closest point algorithm (ICP). As shown in Equation (1), the UAV-SfM generated point cloud dataset (P) can be transformed onto the space of the ALS point cloud dataset (P′) via the scale factor (s), rotation matrix (R), and translation vector (t). Because the UAV-SfM generated point cloud dataset and the ALS point cloud dataset have the same coordinate system, the scaling is supposed to be uniform and very close to 1.0. Given a rigid transformation matrix (T) to integrate both R and t, the registered point cloud dataset ($P^{\prime }$) becomes the product of matrices T and P:

$$P^{\prime }=sR\left(P\right)+t=TP$$

(1)

$$\mathrm{RMSE}=sqrt({{\displaystyle \sum }}_{i=1}^{\mathrm{N}}{\left(p_i^{\prime }-q_i\right)}^2/\mathrm{N})$$

(2)

In this study, the CloudCompare software is used for the ICP processing, in which the UAV scene shape defined by P is registered to the ALS model shape Q. The calculation of the registration transformation in CloudCompare is an iterative process. For each correspondence or paired point ($p_i^{\prime },q_i$), where $p_i^{\prime }\in P^{\prime }\mathrm{and}{q}_i\in Q$, a residual error ($e_i$) is determined as the distance between $p_i^{\prime }$ and $q_i$. Let N be the number of correspondences, the registration error is determined as the root-mean-square error (RMSE) as shown in Equation (2). The iteration process will terminate when the difference of the registration error RMSE between two successive iterations is smaller than the threshold value (τ), which is 1.0 × 10⁻⁶ in this study. The raw point cloud (RPC) after the referencing transformation becomes an ICP registered point cloud and is denoted as UAV-SfM ICPPC. Figure 2 demonstrates the conceptual model of the ICP processing.

Bias-Adjustment by Invariant-Ground-Surface Altitude

Since the forest canopy occupied most of the study areas, the calculated parameters of the transformation matrix tend to be canopy-height oriented. In other words, in cases of registration for forest datasets gathered in different years, the transformed z-value of each point is most likely either overestimated or underestimated. This is relative to primarily the inherent bias in the UAV images’ coordinates and the height growth due to the difference in data acquisition dates. After the ICP processing, the z-coordinate bias is assumed as an additive effect and can be fixed simply by an adjustment factor. Taking the points of the road surface in the areas as the references, the adjustment factor, abbreviated as dz, is determined as:

$$\mathrm{dz}={{\displaystyle \sum }}_{i=1}^n(z_{ia}-z_{ir})/n$$

(3)

where n is the number of the sample point and $z_{ia}$ and $z_{ir}$ stand for the actual value and the registered value of the elevation for point i at the exact location. Relative to the elevation of road surface, a positive/negative value of dz indicates a condition of over/under registration transformation. Therefore, every single point (i) of the registered point cloud dataset P′ whose z-value ($z_{ir}$) is further restored to $z_{ir}^{\prime }$ using the additive formula as shown in Equation (4). After the bias adjustment via the invariant ground surface feature, the finalized UAV-SfM point cloud is considered as bias-free ICPPC and is abbreviated as UAV-SfM BICPPC.

$$z_{ir}^{\prime }=z_{ir}+\mathrm{dz}$$

(4)

UAV-SfM-Based Canopy Height Model Generation

The generated UAV high dense point cloud data, BICPPC, was then rasterized to produce a 0.03 m/pixel of DSM data (DSM_UAV) to retain the performance of areal information in the raw photographs. Taking the ALS-based DEM data as the baseline of topography, the CHM_UAV data of the two forests was determined by subtracting the DEM_ALS from the DSM_UAV of the two study sites. After that, a method using PyCrown [41] was applied to extract the tree height (H_ALS and H_UAV) and crown width (CW_ALS and CW_UAV) of individual trees from the CHM_ALS and CHM_UAV. This method integrates the local maxima filter to identify treetop pixels followed by a watershed segmentation method to delineate the tree crown [16]. Finally, the volumetric parameters of individual trees were used to determine stand parameters. Figure 3 shows the detailed procedures of the point cloud processing for generating gridded surface models and tree parameter estimation.

2.3. Determination of Tree Volumetric Parameters for Both ALS and UAV Datasets

Tree volumetric parameters such as volume (V), height (H), and diameter at breast height (DBH) are generally highly correlated. Therefore, both H and DBH are mainly used to estimate tree volume in forest inventory to support the needs of forest management planning. In unmanaged forests, trees grow freely and tend to be competitive for growth resources in a relatively limited neighboring space. The growth of tree height and diameter will not be homogeneous and probably result in diverse sizes among individual trees [5,12,15]. However, management practices such as pruning and thinning are generally implemented regularly in managed forests, which allow the trees to grow freely under more limited competition. Consequently, the volume, height, diameter, and crown width (CW) of trees in the managed forest can develop following a homogeneous trend and the volumetric parameters of individual trees can be predicted more accurately.

Recently, some studies have investigated the relationship of volumetric parameters of the Hinoki forest based on intensive in situ inventory data and published a variety of allometric models for use in forest management and planning. The DBH-H model (R² = 0.9192, n = 1835), as shown in Equation (5), uses H to predict the DBH of Hinoki trees [42]; in addition, with Equation (6) (R² = 0.9151, n = 608), the DBH can be determined through both predictors H and CW [43]. Integrating both DBH and H variables, tree volume V is determined using Equation (7) [44], a popular volume estimation model in the form of the Schumacher–Hall formula [5]. The H was determined as the most considerable pixel value within the region of a delineated tree crown, and the crown width was defined as CW = 2(CA/π)^0.5, where CA stands for the crown area of a single tree. Correspondingly, the volume of every single tree was predicted using Equation (7), in which DBH was derived from Equation (5) using only H or Equation (6) via both H and CW. To summarize, the DBH derived from Equations (5) and (6) was denoted as _M1DBH and _M2DBH, respectively, and consequently, the resulted volume was marked as _M3V and _M4V.

As previously mentioned, the acquisition date of the ALS data and UAV data has a 6-year or 5-year difference for the Kameyama forest and the Owase forest, respectively. The tree height of the woods in 2013 (@T1 in Figure 3) derived from CHM_ALS should be projected to the particular acquisition year of the UAV datasets (@T2 in Figure 3). According to Nakajima et al. [45], the tree height of the Hinoki can be presented as a function of site index (S) and tree age (t), as shown in Equation (8). With the CHM_ALS determined tree height (H_2013ALS) and the age of the Kameyama and Owase forest stands in 2013 (correspondingly 40 and 60 years), the site index of each of the two forest stands was estimated using Equation (8). After that, based on the age of the Kameyama forest in 2018 and the Owase forest in 2019 (correspondingly 46 and 65 years) and the estimated site index, tree height for the Kameyama forest (H_2018ALS) and the Owase forest (H_2019ALS) was derived. Because the site index is a growth model, DBH and V of every individual tree derived from H_2018ALS or H_2019ALS are labeled as the ALS-GM dataset. Alternatively, the tree parameters derived from H_UAV are classified as the UAV-SfM dataset.

For the stand-level attributes, stand height, stand diameter, stand density, stand basal area, volume stock, and relative spacing were derived from the tree-level data. The stand height and stand diameter are determined as the average H and average DBH of trees over the area of a stand or a plot. Stand density is presented as the number of stems per hectare. Stand basal area and volume stock are calculated as the summation of basal area and volume of trees per hectare. Relative spacing (Sr), the ratio of the average distance between trees to the average dominant height (DoH, m) of the stand, is determined as Sr = (10,000/N)^0.5/DoH, where N is the number of trees per hectare.

DBH = 0.4327H ^1.397

(5)

DBH = 1.3907H + 3.2727CW − 12.3153

(6)

log₁₀ V = −4.31109 + 1.83546 × log₁₀ DBH + 1.10655 × log₁₀ H

(7)

H = (49.4 − 6.98S) (1 − 1.030 × exp(−0.013t))

(8)

2.4. Deriving Annual Growth Rate of Tree Height

In the management of plantation forest, the trees occupy the main canopy, whose heights at the rotation age are generally used to determine the site index of a forest stand. The site index can be further applied to accompany the height observations to project the possible timber production at a particular stand age. In other words, information on tree-height growth is required for managers to carry out planning and recheck how the trees reflect the practices implemented. Thanks to the support of the Mie Prefecture Government, this study collected additional ALS and UAV datasets for examining the following assumptions: integrating ALS-DEM and UAV-SfM-DSM is appropriate for gathering multi-temporal height growth through UAV-SfM-CHM data; the tree height at a particular reference age or year is the baseline value; and the height annual growth rate (HAGR) can be determined for successive periods and further applied to predict height growth for plantation forest management.

The HAGR is presented in a dependent scale (m/yr) and an independent scale (%/yr) of the height measurement. In other words, taking the 2013 ALS as the baseline, the ALS point cloud data acquired in 2020 and UAV-SfM data obtained in 2021 were used to determine the height growth of the Hinoki in 7-year and 8-year growth periods, respectively; and accordingly, the HAGR.

2.5. Assessment of Tree Height and Volume Models Performance

The performance of CHM_ALS and CHM_UAV datasets in estimating the height and volume of individual trees was evaluated via the in situ inventory data. The plot size in the Kameyama and Owase forests was 144 and 244 m², respectively. Each H and DBH of every single tree was determined using Vertex3 and a tape measure on the same date when UAV data was acquired in the inventory. The measures root-mean-square error (RMSE) and percentage root-mean-square error (PRMSE) were applied to evaluate the accuracy of the estimations of tree-level and stand-level parameters. The RMSE has a unit identical to the parameter, and the PRMSE is a relative measure of the RMSE to the average observed data value in percentage.

3. Results

3.1. The Performance of the ICP and Bias-Adjustment Methods in Registering UAV-SfM Point Cloud Data to the ALS Point Cloud Model

Figure 4 shows the point cloud profiles of a cross-section of forest canopy from the study sites. As can be seen in Figure 4a, the UAV-SfM generated raw point cloud (RPC, the yellow points) is distributed above the ALS point cloud (the blue points) with a deviation of more than 30 m in altitude in the Kameyama forest. In contrast, the yellow points aligned below the blue points at about a deviation of 8 m for the Owase forest (Figure 4b). Altitudinal coordinates of the raw point cloud were changed with evident positive/negative biases across the study sites. This discrepancy between the UAV-SfM-derived forest canopy surface and the ALS approach agreed with the first assumption, i.e., the UAV point cloud data should be georeferenced via ground control points to enable accurate retrieving of canopy height.

After the ICP georeferencing transformation, the UAV-SfM point cloud is registered to a space close to the ALS point cloud. The canopy surface of the target point cloud (ICPPC, the orange band) is almost overlapping with the reference point cloud (the blue band) on the same altitudinal level for the Kameyama forest (Figure 4c). However, the orange band appears embedded in the blue band at a lower level for the Owase forest (Figure 4d). In this study, the rotation was set to be three-dimensional, and the translation was set to be along the x-, y-, and z-axes simultaneously. Because the acquisition year of ALS data is 5 years earlier than the UAV data for the Kameyana site and 6 years for the Owase forests, the registered scene shape of UAV-SfM ICPPC should be over-tuned by a certain amount. The amount is most likely close to the height growth of trees during the years and must be calibrated. Taking the average altitude of the ground-surface point cloud surrounding the forest, the constant for bias adjustment is determined as 1.2009 m for the Kameyama forest and 1.3035 m for the Owase forest. Accordingly, the finalized point cloud dataset (BICPPC, the red points) after the bias adjustment by additive rule is shown in Figure 4e,f.

To summarize, 79,425,619 points and 14,949,079 points out of the total points in the raw dataset of the Kameyama and the Owase, respectively, were selected for deriving the rotation matrix (3 × 3) and the translation vector (3 × 1) in the ICP process. The density of the point cloud was 349.05 and 518.90 points per square meter for the Kameyama and Owase sites, which was 15× and 18× more than the density of the ALS point cloud data, respectively. As a result, the rigid transformation matrix, an augmented matrix (4 × 4) composed of the rotation matrix and the translation vector, was derived and used to transform the raw point cloud (the original space) to the registered point cloud (the natural space) for the Hinoki forest at the Kameyama site (Equation (9)) and the Owase site (Equation (10)). The scale factor of Equation (1) was determined as 0.996396 and 0.993830 for the Kameyama and Owase datasets, respectively. Correspondingly, the calculated RMSE was 4.9423 m and 4.4347 m for the Kameyama and Owase forests; and the RMSE was reduced to 1.1569 m and 1.4903 m after the bias adjustment via the road surface elevation. In the transformation matrix, the offsets for the x-, y-, and z-axes were around 31.8 m, 15.3 m, and 31.5 m for the Kameyama forest and 1.1 m, 2.6 m, and −8.0 m for the Owase forest. The value of the z-axis offset 31.8 m and −8.04 m indicates that the UAV-SfM process generated raw point cloud is higher or lower than its natural location by 31.8 m and 8.0 m. The translation distances can be seen in Figure 4a,b.

$$T=\left[\begin{array}{cc}\begin{array}{cc}0.996331& 0.000357\\ -0.00036& 0.996396\end{array}& \begin{array}{cc}-0.01141& 31.756608\\ -0.00002& 15.250034\end{array}\\ \begin{array}{cc}0.011407& 0.000028\\ 0& 0\end{array}& \begin{array}{cc}0.996330& 31.469931\\ 0& 1\end{array}\end{array}\right]\mathrm{for}\mathrm{the}\mathrm{Kameyama}\mathrm{site}$$

(9)

$$T=\left[\begin{array}{cc}\begin{array}{cc}0.993815& -0.00236\\ 0.002338& 0.993819\end{array}& \begin{array}{cc}-0.00489& 1.050710\\ -0.00398& 2.553746\end{array}\\ \begin{array}{cc}0.004895& 0.000028\\ 0& 0\end{array}& \begin{array}{cc}0.993811& -7.99019\\ 0& 1\end{array}\end{array}\right]\mathrm{for}\mathrm{the}\mathrm{Owase}\mathrm{site}$$

(10)

It is very hard to visually recognize points over dense canopy areas as the check points in order to determine the evaluation. Fortunately, there were some solar panels next to the Kameyama forest which are clearly recognizable on the UAV image. Based on CloudCompare, edge points and the three-dimensional coordinates of the solar panels can be easily identified. The corresponding ALS edge points’ locational information was retrieved by colorizing the ALS point clouds with the class attribute, i.e., ground, solar panel, and vegetation. A total of 30 points located on the corners of the panels (as shown in Figure 5) were selected as independent check points for evaluating the geolocation accuracy of the final product of the UAV-SfM point cloud. The coordinates of the check points from the ALS and UAV-SfM datasets listed in

Table 3. Summary of accuracy evaluation of the registered UAV-SfM point cloud dataset (BICPPC).

		ALS			UAV−SfM			Bias
Point ID	x	y	z	x	y	z	xyz	xy	z
1	−117,575.54	336.32	215.89	−117,575.75	336.64	215.82	0.3916	0.0710	0.2724
2	−117,572.46	332.01	213.96	−117,572.59	332.22	213.80	0.2987	0.1650	0.1760
3	−117,600.53	315.30	217.48	−117,600.68	315.74	217.49	0.4629	0.0140	0.3272
4	−117,597.58	311.60	215.68	−117,597.89	311.55	215.55	0.3386	0.1290	0.2214
5	−117,570.15	329.72	214.23	−117,570.26	329.91	214.20	0.2182	0.0260	0.1532
6	−117,567.22	325.50	212.53	−117,567.12	325.49	212.22	0.3267	0.3100	0.0730
7	−117,595.74	309.10	215.77	−117,595.82	309.12	215.61	0.1790	0.1590	0.0582
8	−117,564.66	322.82	212.96	−117,564.79	323.16	212.88	0.3699	0.0760	0.2560
9	−117,561.67	318.90	211.24	−117,561.55	318.78	210.91	0.3699	0.3290	0.1196
10	−117,590.13	302.33	214.19	−117,590.30	302.45	214.02	0.2668	0.1700	0.1454
11	−117,586.45	298.53	212.35	−117,586.59	298.15	212.09	0.4820	0.2610	0.2866
12	−117,559.04	316.23	211.70	−117,559.11	316.35	211.50	0.2412	0.2010	0.0943
13	−117,555.71	311.90	209.19	−117,556.08	312.04	209.49	0.5002	0.3000	0.2830
14	−117,584.61	295.99	212.42	−117,584.87	295.73	212.70	0.4651	0.2820	0.2615
15	−117,580.90	291.07	210.96	−117,581.07	291.48	210.73	0.4990	0.2270	0.3142
16	−117,553.78	309.24	210.20	−117,554.07	309.37	210.00	0.3765	0.2010	0.2251
17	−117,550.79	305.16	207.53	−117,550.63	305.30	208.01	0.5280	0.4830	0.1509
18	−117,578.99	288.58	211.12	−117,579.16	289.03	211.17	0.4828	0.0480	0.3397
19	−117,576.14	284.80	209.35	−117,576.01	284.66	209.19	0.2514	0.1600	0.1371
20	−117,547.91	302.80	208.96	−117,548.17	302.85	208.88	0.2825	0.0850	0.1905
21	−117,544.94	298.68	206.99	−117,545.17	298.63	206.74	0.3391	0.2460	0.1650
22	−117,573.67	282.06	210.05	−117,573.92	282.21	209.90	0.3236	0.1480	0.2035
23	−117,543.53	295.77	207.21	−117,543.40	296.21	207.14	0.4604	0.0730	0.3214
24	−117,539.38	291.46	205.28	−117,539.43	291.90	205.16	0.4622	0.1240	0.3149
25	−117,564.57	271.27	206.19	−117,564.61	271.25	206.34	0.1591	0.1540	0.0281
26	−117,549.53	364.42	214.93	−117,549.22	364.74	214.90	0.4464	0.0280	0.3150
27	−117,546.41	360.27	213.18	−117,546.22	360.39	212.90	0.3588	0.2790	0.1595
28	−117,545.98	343.03	211.55	−117,546.31	343.01	211.36	0.3847	0.1900	0.2365
29	−117,610.64	243.15	208.09	−117,610.46	243.47	208.09	0.3643	0.0010	0.2576
30	−117,607.91	238.14	206.09	−117,607.88	238.56	205.85	0.4822	0.2400	0.2957
RMSE (m)							0.3704	0.1727	0.2128

are based on the JGD2000 coordinate system, Japan Plane Rectangular CS VI. As can be seen, the RMSE in the view of three-dimensional distance (xyz), planar distance (xy), and altitudinal distance (z) was 0.3704 m, 0.1728 m, and 0.2128 m, respectively. Figure 6 demonstrates the possibility of UAV-SfM RPC registration when a need for multiple referencing is raised. The approximation distance between ICPPC2020 and ICPPC2013 shows a high agreement of the two datasets and indicates the proposed algorithm of UAV-SfM RPC processing works. To accomplish the whole UAV-SfM point cloud processing process, the last step is a bias adjustment to account for the effects of canopy growth. After that, the BICPPC datasets based on 2013 and 2020 are finalized. Consequently, the difference of surface height in the road areas between the BICPPC and ALS datasets can be an index of the point alignment performance. To summarize, when the UAV-SfM2019 is georeference transformed based on the ALS2013, the resulted BICPPC dataset has an MAE of 0.0521 ± 0.0360 m, while it was 0.0287 ± 0.0224 m for the case based on ALS2020.

3.2. Tree Segmentation Accuracy of CHM Data via the UAV-SfM and ALS-GM Approaches

In forestry, a management plan is generally prepared to guide forest practice and to derive projected attributes of forest stands. We can either indirectly draw the information via a robust sampling scheme and analysis to meet this end for extensive forestland or directly gather information from a whole inventory task for small forestland. In Figure 7, the treetops and crown boundaries were automatically drawn by CHM image segmentation using a local maximum filtering and watershed segmentation in PyCrown.

Table 4. Evaluation of the number of trees based on the image-interpretation-based manual delineation method and the PyCrown technique-based automatic delineation method.

Area	Method	Ntrees ¶	Dtrees ¶	OE%	EC%	Precision	Recall	F-Score
Kameyama	UAV	99	100	1.0	2.0	0.99	0.98	0.99
	ALS		84	20.2	5.0	0.79	0.94	0.86
Owase	UAV	110	137	5.5	30.0	0.92	0.68	0.79
	ALS		138	9.0	34.5	0.86	0.62	0.72

^¶ Ntrees and Dtrees stand for the number of trees delineated by the manual delineation method and the PyCrown technique, respectively.

summarizes the results of tree detection based on the number of trees delineated by manual and automatic approaches. Of the 99 trees at the Kameyama site, the number of trees detected via UAV-SfM-CHM and ALS-CHM dataset was 100 and 84, respectively, which accounts for a 1.0% and 2.0% of the omission error rate (OE%) and commission error rate (CE%) for the UAV and a 5.0% and 20.2% of the OE% and CE% for the ALS. In this case, the ALS-CHM data appeared to be under-segmented and resulted in a false-negative percentage more significant than the UAV-SfM-CHM. The number of trees at the Owase site was over-estimated for both UAV and ALS datasets. The false-negative rate was lower than 10%, but the false-positive rate was more than 30%. The precision, recall, and F-score are also listed in Table 4.

3.3. Estimated Accuracy of Tree Volumetric Parameters of UAV-SfM and ALS-GM Approaches

3.3.1. Tree Height

Figure 8 shows a scatter plot of the measured and estimated tree height of every single tree in the Kameyama plot and Owase plot. As can be seen on the left of this figure, in the Kameyama forest, tree height determined via ALS₂₀₁₃ point cloud fell onto the space lower than the identity line (x = y) where the difference is caused by tree growth. Tree height determined by the ALS-GM method spread closer to the identity line than ALS₂₀₁₃, indicating that the site index model (Equation (8)) can provide moderate height growth information to compensate for the difficulty of data collection, particularly the acquisition time difference between the ALS data and inventory data. In contrast, the points of the UAV-SfM-determined tree height were distributed around and much closer to the identity line. This indicates that when the tasks of in situ inventory and UAV images acquisition can be accomplished in the same period, the georeferenced UAV-SfM point cloud data could provide appropriate height information of trees. For the Owase forest on the right of Figure 8, the scatter plot revealed that the UAV-SfM method determined that tree heights were also distributed closer to the identity line. The RMSE and PRMSE of the height estimation in the Kameyama forest were 0.81 m and 4.50% for the ALS-GM point cloud dataset, while 0.43 m and 2.40% for the UAV-SfM point cloud dataset (

Table 5. A comparison of tree height determination via the georeferenced UAV-SfM point cloud data and ALS point cloud data.

Site	Dataset	H Estimates Mean ± Std (m)	Estimation Error ¶ Range (m)	Estimation Error Mean ± Std (m)	RMSE (m)	PRMSE (%)
Kameyama	UAV-SfM	18.07 ± 0.55	−0.69–1.29	0.30 ± 0.31	0.43	2.40
	ALS-GM	18.71 ± 0.56	0.13–2.21	0.65 ± 0.48	0.81	4.50
	ALS2013	16.73 ± 0.50	−1.89–0.09	1.34 ± 0.42	1.41	7.78
Owase	UAV-SfM	20.25 ± 1.23	−1.58–1.31	0.91 ± 0.40	0.99	4.73
	ALS-GM	21.82 ± 2.10	−1.64–3.91	1.45 ± 0.80	1.65	7.84
	ALS2013	20.66 ± 1.99	−2.61–2.73	1.14 ± 0.89	1.45	6.87

^¶ Error = estimated − observed, a positive value indicates overestimation and a negative underestimation. The means and std (standard deviation) were calculated based on the absolute error of all sample trees. The ALS₂₀₁₃ provides the estimated height of trees in 2013 that can be a baseline for evaluating the height growth of the stands when integrating the UAV-SfM-determined size of trees in the inventory year.

). In contrast, the bias of height estimation in the Owase forest appeared larger for both ALS-GM and UAV-SfM datasets; correspondingly, the RMSE and PRMSE were 0.99 m and 4.73% and 1.65 m and 7.84%.

3.3.2. Tree Diameter

The diameter of the trees was estimated by the DBH-H model and DBH-H-CA model using the ALS-GM and UAV-SfM datasets. A comparison of measured and predicted values of the study sites is shown in Figure 9. As shown in

Table 6. Summary of diameter estimation and accuracy evaluation for both Kameyama and Owase forest.

Site	Dataset	DBH Equation	Range of Estimates (cm)	Mean ± Std (cm)	RMSE (cm)	PRMSE (%)
Kameyama	ALS-GM	M1: Equation (5)	24.66–28.44	25.91 ± 1.08	2.57	10.47
		M2: Equation (6)	20.43–30.75	24.32 ± 2.50	3.18	12.96
	UAV-SfM	M1: Equation (5)	23.03–26.85	24.67 ± 1.05	2.32	9.48
		M2: Equation (6)	20.25–29.86	23.42 ± 2.43	3.27	13.36
Owase	ALS-GM	M1: Equation (5)	24.84–39.79	32.19 ± 4.30	5.86	18.25
		M2: Equation (6)	21.18–37.49	29.44 ± 3.84	5.58	17.38
	UAV-SfM	M1: Equation (5)	24.94–33.56	28.95 ± 2.46	3.84	11.95
		M2: Equation (6)	21.25–32.95	27.25 ± 3.25	4.73	14.75

, the DBH-H model had an RMSE and PRMSE of 2.57 m and 10.47% in the estimation of _M1DBH_ALS-GM and 2.32 m and 9.48% in the estimation of _M1DBH_UAV-SfM for the Kameyama forest. This indicates that the DBH-H model has a similar performance of diameter estimation using both the ALS-GM and the UAV-SfM point cloud datasets in the stand with commercial-thinning ages. However, this similarity was not observed in the matured forest in the Owase site. As shown in Table 6, the estimation through the UAV-SfM dataset was better with an RMSE and PRMSE of 3.84 m and 11.95%, where the improvement was around 2 m and 6%.

Unfortunately, the results show that the DBH-H-CA model is not superior in tree diameter characterization for middle-aged and matured forest stands. The RMSE and PRMSE of DBH estimation achieved by Equation (8) are mostly more prominent than Equation (5) except for the estimation through the ALS-GM dataset in the Owase forest. Tree crown size generally expands in accordance with the growth of tree size. However, it is also highly subject to intensive pruning until commercial thinning for timber-production forests. The results suggested that with tree height and canopy width used simultaneously as predictors for DBH estimation it is highly possible to introduce uncertainty and impact the estimation accuracy in a low-intensity managed forest. In general, a thinning will lead to tree growth release, extending outward and leading the forest canopy to close again in a relatively short period. A reasonable period for deriving tree parameters by the UAV-SfM-CHM segmentation is approximately ten years.

3.3.3. Tree Volume

Integrating the point-cloud-determined tree height and the model-derived diameter estimate, the volume of every single tree is calculated. According to the sources of tree parameters, the volume of every single tree is determined using Equation (7) and named _M3V_ALS-GM, _M4V_ALS-GM, _M3V_UAV-SfM, and _M4V_UAV-SfM, where M3 and M4 indicate the combination of DBH and volume models and ALS-GM and UAV-SfM are the point-could datasets, respectively. The estimation is summarized in

Table 7. Summary of the tree volume estimation and accuracy evaluation for the Kameyama and Owase forests.

Site	Dataset	Volume Equation	Range of Estimates (m3)	Mean ± Std (m3)	RMSE (m3)	PRMSE (%)
Kameyama	ALS-GM	M3: Equations (5) and (7)	0.4312–0.6271	0.4929 ± 0.0561	0.0940	21.92
		M4: Equations (6) and (7)	0.3129–0.7172	0.4430 ± 0.1017	0.1117	26.05
	UAV-SfM	M3: Equations (5) and (7)	0.3603–0.5394	0.4332 ± 0.0494	0.0777	18.11
		M4: Equations (6) and (7)	0.2956–0.6555	0.3975 ± 0.0921	0.1092	25.47
Owase	ALS-GM	M3: Equations (5) and (7)	0.4393–1.5162	0.9016 ± 0.3062	0.3406	40.33
		M4: Equations (6) and (7)	0.3280–1.3533	0.7619 ± 0.2567	0.2849	33.73
	UAV-SfM	M3: Equations (5) and (7)	0.4407–1.3105	0.8187 ± 0.2416	0.2280	26.99
		M4: Equations (6) and (7)	0.3290–1.1468	0.6953 ± 0.2089	0.2146	25.40

. The scatter plot of estimated and measured values of tree volume, as shown in Figure 10, looks very similar to the pattern of the DBH scatter plot in Figure 9. Accurate measures of RMSE and PRMSE revealed that _M3V_UAV-SfM made a better estimation for the Kameyama forest and _M4V_UAV-SfM for the Owase forest with 0.0777 m/18.11% and 0.2146 m/25.40%, respectively. Because _M3V_UAV-SfM achieved a performance (0.2280 m RMSE/26.99% PRMSE) very close to _M4V_UAV-SfM for the Owase forest, it is also recommended for simplicity using the tree-height-based diameter model and corresponding Schumacher–Hall volume model for tree volume estimation.

In general, tree volume determination of forest stands is rarely conducted only at one specific age of the stand. For any plantation forests, there will have been a series of pre-commercial thinning and commercial thinning before harvesting. In other words, forest managers must evaluate tree parameters of the stands at different ages to generate thinning scenarios during forest development. Integrating all sample trees from the plots in the middle-aged and matured stands as a whole dataset, a validation of volume estimation with a wide range of tree sizes can provide insight into characterizing tree volume and even the volume stock of forests. As mentioned previously, the average and standard deviation of the volume of every single tree was 0.4287 ± 0.0836 m³ for the Kameyama forest and 0.8446 ± 0.2464 m³ for the Owase forest. Therefore, the integrated dataset has an average volume of 0.6806 ± 0.2843 m³ and a minimum/maximum value of 20.50/40.80 cm and 16.90/30.60 m for diameter and height. As a result, the bar charts in Figure 11 show the histogram of estimation errors for the _M3V_ALS-GM, _M4V_ALS-GM, _M3V_UAV-SfM, and _M4V_UAV-SfM. Correspondingly, the RMSE was 0.28 m, 0.24 m, 0.22 m, and 0.23 m³ and the PRMSE was 40%, 35%, 33%, and 34%. The integrated dataset evaluation received an RMSE similar to the site-specific evaluation but this is not the case with the PRMSE, as shown in Table 7. As the PRMSE measures the ratio of the RMSE against the average, the increase in the PRMSE is mainly contributed by the change in average tree volume of the dataset. In other words, the middle-aged forest and mature forest average volume had significantly increased/decreased in contrast to its original value, respectively. This suggests the estimation and evaluation of tree parameters should be stand oriented.

4. Discussion

4.1. Performance of UAV-SfM Point Cloud Data in Characterizing Stand-Level Attributes

Based on the automatic segmentation of the UAV-SfM-CHM and ALS-CHM datasets,

Table 8. Summary of stand-level parameters derived from UAV-SfM-CHM and ALS-CHM datasets.

Stand Parameter/Index	Kameyama Site					Owase Site
	Ground	UAV	E% ¶	ALS	E%	Ground	UAV	E%	ALS	E%
Stand density (N, tree/ha)	1042	1042	0.00	903	−13.34	943	943	0.00	943	0.00
Average stem diameter (cm)	24.49	24.67	0.73	25.91	5.80	32.09	29.00	−9.63	32.19	0.31
Average stem height (m)	18.06	18.07	0.06	18.71	3.60	21.04	20.20	−3.99	21.82	3.71
Average stem volume (m3)	0.43	0.43	1.05	0.49	14.98	0.84	0.82	−3.07	0.90	6.75
Volume per plot (m3)	6.43	6.50	1.03	7.39	14.97	19.43	18.83	−3.07	20.74	6.74
Stand volume stock (m3/ha)	446.59	451.21	1.03	513.43	14.97	796.17	771.72	−3.07	849.82	6.74
Stand basal area (m2/ha)	49.61	49.87	0.52	55.02	0.91	77.47	62.49	−19.34	78.09	0.80
Sr (%)	17.20	16.70	−2.91	16.60	−3.49	15.40	16.00	3.90	15.20	−1.30

^¶ E% = (Estimate − Observation)/Observation ∗ 100 is a measure of bias for the estimation made by the CHM segmentation. In which the negative sign indicates an underestimation.

summarizes the stand parameters of the Kameyama and Owase forests. In forestry, the average value of the height and that of the diameter of every tree is used to account for the attributes of height and diameter at the stand level. The stand-level volume stock is presented as the aggregated value of volume or basal area of every single tree. In addition, the relative spacing (Sr) is generally used as a guide for managing the stand density. In Table 8, the E% is defined as the percentage of an estimate that deviates from the observed value. A positive/negative value stands for an over/under-estimation. As noted, the UAV approach was estimated with an E% less than 3% for each of the stand parameters for the Kameyama site, while from 0% to 20% for the Owase site. The ALS approach achieved a more significant estimation bias for the Kameyama than the Owase site.

By checking the segmentation evaluation in Table 4 and the UAV-RGB images of the forests in Figure 1, some space remains in the canopy for trees to develop in the Kameyama forest but appears almost absent in the Owase forest. This indicates that the tree crown of the 65-year-old Hinoki stand seems to grow freely on the top, resulting in multiple convex features, leading to different image segments. Therefore, a significant false-negative error rate occurred in the number of trees estimated at the Owase site for both the UAV-SfM-CHM and ALS-CHM datasets. In contrast, the 46-year-old Hinoki stand has a unimodal shape which is a standard crown feature. Therefore, automatic image segmentation on the UAV and ALS datasets works very well in the Kameyama site. This further suggests that the combination of the UAV-SfM-DSM and ALS-DEM has good potential in deriving multi-temporal UAV-SfM-CHM for applications, particularly for intensive management of timber plantations. Accordingly, the stand parameters of the younger Hinoki stands could be derived appropriately. Suppose a management plan can define a suitable cycle of pre-commercial thinning and commercial thinning practices. In that case, the canopy feature of a mature forest remains optimistic for deriving tree parameters at high accuracy.

4.2. The Potential of Deriving Height Growth Information for Forest Monitoring via Integration of ALS and UAV-SfM Data

In addition to those mentioned in the previous section, further samples of 480 trees, aged between 37 and 82, were collected from 11 plots located in the Kameyama area. As shown in

Table 9. Height annual growth rate of the Hinoki trees over a wide range of stand ages.

Descriptive Statistics	Age Years)	ALS_HAGR (m/yr)	ALS_HAGR (%/yr)	UAV_HAGR (m/yr)	UAV_HAGR (%/yr)
Minimum	37	0.06	0.36	0.09	0.81
Maximum	82	0.47	6.07	0.52	4.96
Average	57.38	0.30	2.59	0.31	2.66
STD	17.71	0.08	1.09	0.06	0.84

, the ALS-CHM approach determined HAGR was 0.30 ± 0.08 m, accounting for an increment rate of 2.59 ± 1.09% in respect to the height baseline in 2013 at the tree-level perspective. Alternatively, the HAGR determined by the UAV-SfM-CHM approach was 0.31 ± 0.06 m, equivalent to 2.66 ± 0.84% of the height in 2013. The average HAGR difference between the UAV and ALS approaches was 0.01 m/yr or 0.07 %/yr. The similarity of the UAV-SfM-CHM and ALS-CHM tree-height estimates is shown in Figure 12. As can be seen, the estimates of height and HAGR of individual trees made by the two systems have a linear relationship with an R-squared of 0.9825 and 0.7760, respectively, and each is significant at the probability level α = 0.01. Though the HAGR estimates of the UAV approach appeared slightly smaller/larger than the ALS approach for those trees with a larger/smaller annual growth rate, the difference in estimates is small enough that a high agreement can be concluded.

In forestry, the increment rate of tree height is generally assumed as linear for a relatively short growth period, for example, 5 or 10 years. However, as noted in Figure 13, the HAGR (%) of the Hinoki trees behave as an exponential decay function of the tree height, indicating the height increment percentage of the trees is gradually decreased exponentially as stand age increases. Taking the height of trees measured from the 2013 ALS dataset as the baseline, the exponential decay model (Equation (11)) derived via the ALS-based approach has a slope larger than the UAV-based approach (Equation (12)). The R-squared of the ALS-based and UAS-based HAGR% model was 0.6203 (n = 480, p < 0.0001) and 0.5915 (n = 480, p < 0.0001), respectively. This finding provides new evidence for the need to model tree growth and forest growth. It enables continuous forest inventory through remote sensing data to gather reliable spatiotemporal data to realize sustainable timber production planning and practice.

To collect multi-temporal data over small forestland via a UAV is implementable as a routine task at a low cost. However, the system is subject to the strength and endurance ability of the UAV system to meet the needs of data collection for a large area of forestland. To this end, a spaceborne lidar system designed to collect complex waveform data or photon lidar data over a larger footprint might be an alternative. As an existing forest monitoring system integrating multi-source remote sensing data [46], the harmonized full-waveform metrics-based stand height modeling technique [47] could be helpful to retrieve stand-level attributes for forest planning via an area-based approach [15,48]. Recalling the bi-temporal point cloud referencing transformation mentioned in Section 3.1, the proposed algorithm can be applied to collect multi-temporal canopy height information of a forest stand to support in situ data for validating satellite and airborne lidar systems in the view of conducting a plot-based inventory.

$$\mathrm{HAGR}(\%)=0.4397+10.7709\left(\exp \left(-0.1358\mathrm{H}\right)\right),\mathrm{for}\mathrm{the}\mathrm{ALS}-\mathrm{based}\mathrm{approach}$$

(11)

$$\mathrm{HAGR}(\%)=0.4842+6.9310\left(\exp \left(-0.0961\mathrm{H}\right)\right),\mathrm{for}\mathrm{the}\mathrm{UAV}-\mathrm{based}\mathrm{approach}$$

(12)

4.3. An Additional View on the Use of Enterprise-Grade UAV-Based Sensors for Forest Inventory

The development of remote sensing technology has significantly increased the opportunity for foresters to utilize various UAV-based sensors for forest inventory. For the UAV-SfM technique, a consumer-grade UAV can be applied to generate accurate DEM data with the support of predefined GCPs when forest canopy closure is significantly low or the forest has just been harvested. However, the UAV-SfM technique still needs to integrate with accurate high-resolution DEM data to support tree height derivation and related tree-level parameters; this is particularly significant for dense forests. It can contribute to canopy height normalization and further satisfy the need for retrieving tree parameters to achieve precise management of plantation forests. Although forest canopy surfaces can be generated accurately when an enterprise-grade UAV is equipped with an RTK-based RGB, multispectral, and lidar system, the integration of UAV-SfM and ALS point cloud data remain essential for dense forests. This is because rare ground point clouds can be received under forests with high canopy closure. This can contribute to meeting the need for precise management of plantation forests.

5. Conclusions

Continuous forest inventory is essential and requires forest managers to constantly collect forest attributes for designing and implementing regular management practices. Airborne lidar sensors and unmanned-aerial systems are important tools as they can collect data with accurately depicted canopy features for forest inventory from the air. The performance of retrieving tree parameters from the remotely sensed data is critical to realizing the continuous forest inventory for timber production management. Producing high-quality timber depends on proper management and intensive forest practices, including regeneration, pre-commercial thinning, timber harvesting, etc. Forest management planning highly relies on detailed and precise forest information. As noted, automatic tree detection and crown delineation are implemented through segmentation techniques using point-based or image-based data. However, for practical reasons, the segmentation in economic forests with highly dense canopy remains challenging if merely using ALS-based point cloud data or canopy height model data. For example, (1) multi-temporal high-resolution data is required for monitoring forest status and retrieving tree attributes over a long period of management. However, the cost of gathering high-density ALS data deters the managers from regularly utilizing this approach. (2) With data collection using a lower pulse rate lidar scheme, the treetops are most likely miss-hit; consequently, their features are not shown in the point cloud data. When drawing individual trees from such lower density point cloud data or its derivative canopy height model data, the false-negative and false-positive errors tend to occur in dense forests.

The UAV dataset may improve tree detection because the UAV-SfM method provides dense point cloud data, which catches the details of treetops and crown edges more precisely as no shadow effect occurs in the dataset. It is also obtained at significantly lower costs. A lower density of ALS point cloud, for example, one point per square meter, is sufficient to provide terrain morphology of the forest land and is thus able to support high-resolution DEM data for the managers to integrate multi-temporal UAV-SfM point cloud data to generate a series of canopy height model data for applications. This protocol of applying ICP registration transformation with a reference-height adjustment method can efficiently register the point cloud of a UAV equipping without an RTK instrument data to ALS point cloud. In addition, the ALS point cloud can provide ground surface data as material for normalizing UAV-SfM generated point cloud data and generating canopy height model data for extracting tree attributes. This study has demonstrated optimistic results in estimating individual trees’ height and increment rate in plantation forests. The stand-level parameters such as the number of trees, basal areas, and standing volume stocks per hectare are also retrievable from the tree-level parameters derived by the UAV-SfM-based approach at an acceptable accuracy with an error rate ranging from 7% to 15%. The proposed protocol can gather detailed information of a forest at tree-level parameters and stand-level attributes; the changes of a forest can be retrieved at a higher temporal frequency and low cost. Therefore, this approach is beneficial for monitoring forest development and creating scenarios to synchronize forest zoning [49] and timber harvest [50] for appropriate management and profitability.

To summarize, applying ALS and UAV-SfM point cloud data to collect tree-level parameters has an excellent performance in height measurement but remains challenged with regards to measurement accuracy in situ. In general, trees compete for nutrients and space for growth. A competition index that integrates the metrics of tree height and the distance between object–tree and neighboring trees is useful in describing the variation of tree diameter for the ALS approach. Canopy features such as crown area, crown length, or crown depth, and even the height below the canopy, can be directly or indirectly measured from the lidar data and are of benefit in diameter estimation [12,15,21]. However, the importance of such tree-level parameters in estimating diameter appeared not significant in intensively managed plantation forests. There is a need to investigate a model that can integrate the high-performance of tree height measurement and stand-level attributes for tree-level diameter and volume estimation.