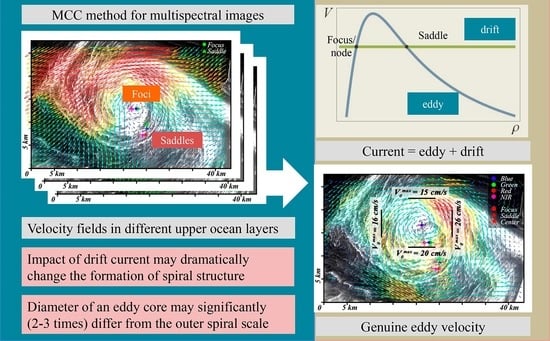
Manifestation of Spiral Structures under the Action of Upper Ocean Currents
Abstract
:1. Introduction
2. Materials and Methods
3. Analytical Description
4. Discussion
- (1)
- the geometry of the resulting current streamlines qualitatively differs from the genuine structure of marine eddies;
- (2)
- the velocity field may demonstrate the presence of a second equilibrium point, i.e., the saddle;
- (3)
- the position of the focus/node (which corresponds to the spiral center) depends on the drift current and may be significantly shifted from the eddy center—up to the scale of the eddy core.
- (1)
- the manifestation of marine eddies due to algae bloom is a seasonal effect;
- (2)
- the study of regions with an extensive phytoplankton blooming is required;
- (3)
- focus on deep-sea eddies not affected by ocean bathymetry is required;
- (4)
- high-resolution images are required to observe small-scale inner structure of the upper-ocean velocity field;
- (5)
- according to our estimations, in order to observe the described features and to adequately apply the MCC method, the time intervals between the images should not exceed the order of 0.5–1 h; these coupled observations are quite rare;
- (6)
- even if the described conditions are fulfilled, the cloud coverage should be low in order not to affect the results of ocean surface observations.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eldevik, T.; Dysthe, K.B. Spiral eddies. J. Phys. Oceanogr. 2002, 32, 851–869. [Google Scholar] [CrossRef]
- Munk, W.; Armi, L.; Fischer, K.; Zachariasen, F. Spirals on the sea. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2000, 456, 1217–1280. [Google Scholar] [CrossRef]
- Groeskamp, S.; LaCasce, J.H.; McDougall, T.J.; Rogé, M. Full-depth global estimates of ocean mesoscale eddy mixing from observations and theory. Geophys. Res. Lett. 2020, 47, e2020GL089425. [Google Scholar] [CrossRef]
- McGillicuddy, D.J., Jr.; Johnson, R.; Siegel, D.A.; Michaels, A.F.; Bates, N.R.; Knap, A.H. Mesoscale variations of biogeochemical properties in the Sargasso Sea. J. Geophys. Res. Ocean. 1999, 104, 13381–13394. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Xu, Y.; Zhang, X.; Huang, C. Global chlorophyll distribution induced by mesoscale eddies. Remote Sens. Environ. 2021, 254, 112245. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.-R.; Chai, F.; Yuan, Y. Impact of mesoscale eddies on chlorophyll variability off the coast of Chile. PLoS ONE 2018, 13, e0203598. [Google Scholar] [CrossRef]
- Griffies, S.M.; Winton, M.; Anderson, W.G.; Benson, R.; Delworth, T.L.; Dufour, C.O.; Dunne, J.P.; Goddard, P.; Morrison, A.K.; Rosati, A.; et al. Impacts on ocean heat from transient mesoscale eddies in a hierarchy of climate models. J. Clim. 2015, 28, 952–977. [Google Scholar] [CrossRef]
- Shan, X.; Jing, Z.; Gan, B.; Wu, L.; Chang, P.; Ma, X.; Wang, S.; Chen, Z.; Yang, H. Surface heat flux induced by mesoscale eddies cools the Kuroshio-Oyashio Extension region. Geophys. Res. Lett. 2020, 47, e2019GL086050. [Google Scholar] [CrossRef]
- Klein, P.; Lapeyre, G. The oceanic vertical pump induced by mesoscale and submesoscale turbulence. Annu. Rev. Mar. Sci. 2009, 1, 351–375. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Qiu, B. Surface Chlorophyll Enhancement in Mesoscale Eddies by Submesoscale Spiral Bands. Geophys. Res. Lett. 2020, 47, e2020GL088820. [Google Scholar] [CrossRef]
- Guerrero, L.; Sheinbaum, J.; Mariño-Tapia, I.; González-Rejón, J.J.; Pérez-Brunius, P. Influence of mesoscale eddies on cross-shelf exchange in the western Gulf of Mexico. Cont. Shelf Res. 2020, 209, 104243. [Google Scholar] [CrossRef]
- Zatsepin, A.G.; Baranov, V.I.; Kondrashov, A.A.; Korzh, A.O.; Kremenetskiy, V.V.; Ostrovskii, A.G.; Soloviev, D.M. Submesoscale eddies at the Caucasus Black Sea shelf and the mechanisms of their generation. Oceanology 2011, 51, 554–567. [Google Scholar] [CrossRef]
- DiGiacomo, P.M.; Holt, B. Satellite observations of small coastal ocean eddies in the Southern California Bight. J. Geophys. Res. Ocean. 2001, 106, 22521–22543. [Google Scholar] [CrossRef]
- Ivanov, A.Y.; Ginzburg, A.I. Oceanic eddies in synthetic aperture radar images. J. Earth Syst. Sci. 2002, 111, 281. [Google Scholar] [CrossRef] [Green Version]
- Stuhlmacher, A.; Gade, M. Statistical analyses of eddies in the Western Mediterranean Sea based on Synthetic Aperture Radar imagery. Remote Sens. Environ. 2020, 250, 112023. [Google Scholar] [CrossRef]
- Bashmachnikov, I.L.; Kozlov, I.E.; Petrenko, L.A.; Glok, N.I.; Wekerle, C. Eddies in the North Greenland Sea and Fram Strait from satellite altimetry, SAR and high-resolution model data. J. Geophys. Res. Ocean. 2020, 125, e2019JC015832. [Google Scholar] [CrossRef]
- Chen, G.; Han, G.; Yang, X. On the intrinsic shape of oceanic eddies derived from satellite altimetry. Remote Sens. Environ. 2019, 228, 75–89. [Google Scholar] [CrossRef]
- Early, J.J.; Samelson, R.M.; Chelton, D.B. The evolution and propagation of quasigeostrophic ocean eddies. J. Phys. Oceanogr. 2011, 41, 1535–1555. [Google Scholar] [CrossRef]
- Fu, L.L.; Le Traon, P.Y. Satellite altimetry and ocean dynamics. C. R. Geosci. 2006, 338, 1063–1076. [Google Scholar] [CrossRef] [Green Version]
- Chapman, R.D.; Shay, L.K.; Graber, H.C.; Edson, J.B.; Karachintsev, A.; Trump, C.L.; Ross, D.B. On the accuracy of HF radar surface current measurements: Intercomparisons with ship-based sensors. J. Geophys. Res. Ocean. 1997, 102, 18737–18748. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Kubryakov, A.A.; Stanichny, S.V.; Zatsepin, A.G.; Kremenetskiy, V.V. Long-term variations of the Black Sea dynamics and their impact on the marine ecosystem. J. Mar. Syst. 2016, 163, 80–94. [Google Scholar] [CrossRef]
- Lebedev, S.A.; Kostianoy, A.G. Satellite Altimetry of the Caspian Sea; Sea: Moscow, Russia, 2005; p. 366. [Google Scholar]
- Raj, R.P.; Johannessen, J.A.; Eldevik, T.; Nilsen, J.Ø.; Halo, I. Quantifying mesoscale eddies in the Lofoten Basin. J. Geophys. Res. Ocean. 2016, 121, 4503–4521. [Google Scholar] [CrossRef]
- Rio, M.H.; Santoleri, R. Improved global surface currents from the merging of altimetry and sea surface temperature data. Remote Sens. Environ. 2018, 216, 770–785. [Google Scholar] [CrossRef]
- Kurkin, A.; Kurkina, O.; Rybin, A.; Talipova, T. Comparative analysis of the first baroclinic Rossby radius in the Baltic, Black, Okhotsk, and Mediterranean seas. Russ. J. Earth Sci. 2020, 20, ES4008. [Google Scholar] [CrossRef]
- Müller, F.L.; Wekerle, C.; Dettmering, D.; Passaro, M.; Bosch, W.; Seitz, F. Dynamic ocean topography of the northern Nordic seas: A comparison between satellite altimetry and ocean modeling. Cryosphere 2019, 13, 611–626. [Google Scholar] [CrossRef] [Green Version]
- Volkov, D.L.; Pujol, M.I. Quality assessment of a satellite altimetry data product in the Nordic, Barents, and Kara seas. J. Geophys. Res. Ocean. 2012, 117, C03025. [Google Scholar] [CrossRef] [Green Version]
- Emery, W.J.; Thomas, A.; Collins, M.; Crawford, W.R.; Mackas, D. An objective method for computing advective surface velocities from sequential infrared satellite images. J. Geophys. Res. Ocean. 1986, 91, 12865–12878. [Google Scholar] [CrossRef] [Green Version]
- Emery, W.; Fowler, C.; Clayson, C. Satellite-image-derived Gulf Stream currents compared with numerical model results. J. Atmos. Ocean. Technol. 1992, 9, 286–304. [Google Scholar] [CrossRef] [Green Version]
- Dransfeld, S.; Larnicol, G.; Le Traon, P.Y. The potential of the maximum cross-correlation technique to estimate surface currents from thermal AVHRR global area coverage data. IEEE Geosci. Remote Sens. Lett. 2006, 3, 508–511. [Google Scholar] [CrossRef]
- Gade, M.; Seppke, B.; Dreschler-Fischer, L. Mesoscale surface current fields in the Baltic Sea derived from multi-sensor satellite data. Int. J. Remote Sens. 2012, 33, 3122–3146. [Google Scholar] [CrossRef]
- Kozlov, I.E.; Plotnikov, E.V.; Manucharyan, G.E. Brief Communication: Mesoscale and submesoscale dynamics in the marginal ice zone from sequential synthetic aperture radar observations. Cryosphere 2020, 14, 2941–2947. [Google Scholar] [CrossRef]
- Marmorino, G.O.; Smith, G.B.; North, R.P.; Baschek, B. Application of airborne infrared remote sensing to the study of ocean submesoscale eddies. Front. Mech. Eng. 2018, 4, 10. [Google Scholar] [CrossRef]
- Notarstefano, G.; Poulain, P.M.; Mauri, E. Estimation of surface currents in the Adriatic Sea from sequential infrared satellite images. J. Atmos. Ocean. Technol. 2008, 25, 271–285. [Google Scholar] [CrossRef]
- Castellanos, P.; Pelegrí, J.L.; Baldwin, D.; Emery, W.J.; Hernández-Guerra, A. Winter and spring surface velocity fields in the Cape Blanc region as deduced with the maximum cross-correlation technique. Int. J. Remote Sens. 2013, 34, 3587–3606. [Google Scholar] [CrossRef]
- Chen, W. Nonlinear inverse model for velocity estimation from an image sequence. J. Geophys. Res. Ocean. 2011, 116, C06015. [Google Scholar] [CrossRef] [Green Version]
- Osadchiev, A.; Sedakov, R. Spreading dynamics of small river plumes off the northeastern coast of the Black Sea observed by Landsat 8 and Sentinel-2. Remote Sens. Environ. 2019, 221, 522–533. [Google Scholar] [CrossRef]
- Aleskerova, A.; Kubryakov, A.; Stanichny, S.; Medvedeva, A.; Plotnikov, E.; Mizyuk, A.; Verzhevskaia, L. Characteristics of topographic submesoscale eddies off the Crimea coast from high-resolution satellite optical measurements. Ocean Dyn. 2021, 71, 655–677. [Google Scholar] [CrossRef]
- Sun, H.; Song, Q.; Shao, R.; Schlicke, T. Estimation of sea surface currents based on ocean colour remote-sensing image analysis. Int. J. Remote Sens. 2016, 37, 5105–5121. [Google Scholar] [CrossRef]
- Bowen, M.M.; Emery, W.J.; Wilkin, J.L.; Tildesley, P.C.; Barton, I.J.; Knewtson, R. Extracting multiyear surface currents from sequential thermal imagery using the maximum cross-correlation technique. J. Atmos. Ocean. Technol. 2002, 19, 1665–1676. [Google Scholar] [CrossRef] [Green Version]
- Qazi, W.A.; Emery, W.J.; Fox-Kemper, B. Computing ocean surface currents over the coastal California current system using 30-min-lag sequential SAR images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7559–7580. [Google Scholar] [CrossRef]
- Marmorino, G.O.; Holt, B.; Molemaker, M.J.; DiGiacomo, P.M.; Sletten, M.A. Airborne synthetic aperture radar observations of “spiral eddy” slick patterns in the Southern California Bight. J. Geophys. Res. Ocean. 2010, 115, C05010. [Google Scholar] [CrossRef] [Green Version]
- Danilicheva, O.A.; Ermakov, S.A.; Kapustin, I.A. Retrieval of surface currents from sequential satellite radar images. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli Iz Kosm. 2020, 17, 93–96. [Google Scholar] [CrossRef]
- Marmorino, G.; Chen, W. Use of WorldView-2 along-track stereo imagery to probe a Baltic Sea algal spiral. Remote Sens. 2019, 11, 865. [Google Scholar] [CrossRef] [Green Version]
- Delandmeter, P.; Lambrechts, J.; Marmorino, G.O.; Legat, V.; Wolanski, E.; Remacle, J.-F.; Chen, W.; Deleersnijder, E. Submesoscale tidal eddies in the wake of coral islands and reefs: Satellite data and numerical modelling. Ocean Dyn. 2017, 67, 897–913. [Google Scholar] [CrossRef]
- Liu, T.; Merat, A.; Makhmalbaf, M.; Fajardo, C.; Merati, P. Comparison between optical flow and cross-correlation methods for extraction of velocity fields from particle images. Exp. Fluids 2015, 56, 166. [Google Scholar] [CrossRef]
- Yang, Z.; Johnson, M. Hybrid particle image velocimetry with the combination of cross-correlation and optical flow method. J. Vis. 2017, 20, 625–638. [Google Scholar] [CrossRef] [Green Version]
- Crocker, R.I.; Matthews, D.K.; Emery, W.J.; Baldwin, D.G. Computing coastal ocean surface currents from infrared and ocean color satellite imagery. IEEE Trans. Geosci. Remote Sens. 2007, 45, 435–447. [Google Scholar] [CrossRef]
- Doronzo, B.; Taddei, S.; Brandini, C.; Fattorini, M. Extensive analysis of potentialities and limitations of a maximum cross-correlation technique for surface circulation by using realistic ocean model simulations. Ocean Dyn. 2015, 65, 1183–1198. [Google Scholar] [CrossRef]
- ECMWF Reanalysis v5 (ERA5). Available online: https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5 (accessed on 29 December 2021).
- Kratzer, S.; Håkansson, B.; Sahlin, C. Assessing Secchi and photic zone depth in the Baltic Sea from satellite data. Ambio 2003, 32, 577–585. [Google Scholar] [CrossRef]
- Danilicheva, O.A.; Ermakov, S.A.; Kapustin, I.A.; Lavrova, O.Y. Characterization of surface currents from subsequent satellite images of organic slicks on the sea surface. In Proceedings SPIE Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 11150, p. 111501R. [Google Scholar] [CrossRef]
- Huang, H.; Dabiri, D.; Gharib, M. On errors of digital particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1427. [Google Scholar] [CrossRef] [Green Version]
- Wirtz, K.; Smith, S.L. Vertical migration by bulk phytoplankton sustains biodiversity and nutrient input to the surface ocean. Sci. Rep. 2020, 10, 1142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nobach, H.; Bodenschatz, E. Limitations of accuracy in PIV due to individual variations of particle image intensities. Exp. Fluids 2009, 47, 27–38. [Google Scholar] [CrossRef] [Green Version]
- Mullaney, T.J.; Suthers, I.M. Entrainment and retention of the coastal larval fish assemblage by a short-lived, submesoscale, frontal eddy of the East Australian Current. Limnol. Oceanogr. 2013, 58, 1546–1556. [Google Scholar] [CrossRef] [Green Version]
- Lévy, M.; Ferrari, R.; Franks, P.J.; Martin, A.P.; Rivière, P. Bringing physics to life at the submesoscale. Geophys. Res. Lett. 2012, 39, L14602. [Google Scholar] [CrossRef] [Green Version]
- Davies, A.; Kwong, S.; Flather, R. The wind induced circulation and the interaction of wind forced and tidally driven currents on the European Shelf. Estuar. Coast. Shelf Sci. 2001, 53, 493–521. [Google Scholar] [CrossRef]
- Shomina, O.V.; Tarasova, T.V.; Danilicheva, O.A.; Kapustin, I.A. Manifestation of sub mesoscale marine eddies in the structure of surface slick bands. In Proceedings SPIE Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; Volume 11529, p. 115290H. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Vol. VI: Hydrodynamics. Theoretical Physics, 4th ed.; M. Science: Moscow, Russia, 1986; p. 736. [Google Scholar]
- Budéus, G.; Cisewski, B.; Ronski, S.; Dietrich, D.; Weitere, M. Structure and effects of a long lived vortex in the Greenland Sea. Geophys. Res. Lett. 2004. [Google Scholar] [CrossRef]
- Nencioli, F.; Kuwahara, V.S.; Dickey, T.D.; Rii, Y.M.; Bidigare, R.R. Physical dynamics and biological implications of a mesoscale eddy in the lee of Hawai’i: Cyclone Opal observations during E-Flux III. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2008, 55, 1252–1274. [Google Scholar] [CrossRef]
- Hu, Z.Y.; Petrenko, A.A.; Doglioli, A.M.; Dekeyser, I. Study of a mesoscale anticyclonic eddy in the western part of the Gulf of Lion. J. Mar. Syst. 2011, 88, 3–11. [Google Scholar] [CrossRef]
- Baker, C.J.; Sterling, M. Modelling wind fields and debris flight in tornadoes. J. Wind Eng. Ind. Aerodyn. 2017, 168, 312–321. [Google Scholar] [CrossRef]
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar] [CrossRef]
- Vatistas, G.H.; Kozel, V.; Mih, W.C. A simpler model for concentrated vortices. Exp. Fluids 1991, 11, 73–76. [Google Scholar] [CrossRef]
- Kuwahara, V.S.; Nencioli, F.; Dickey, T.D.; Rii, Y.M.; Bidigare, R.R. Physical dynamics and biological implications of Cyclone Noah in the lee of Hawai’i during E-Flux I. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2008, 55, 1231–1251. [Google Scholar] [CrossRef]
- de Souza, R.B.; Mata, M.M.; Garcia, C.A.; Kampel, M.; Oliveira, E.N.; Lorenzzetti, J.A. Multi-sensor satellite and in situ measurements of a warm core ocean eddy south of the Brazil–Malvinas Confluence region. Remote Sens. Environ. 2006, 100, 52–66. [Google Scholar] [CrossRef] [Green Version]
- Arístegui, J.; Tett, P.; Hernández-Guerra, A.; Basterretxea, G.; Montero, M.F.; Wild, K.; Sangrá, P.; Hernández-León, S.; Canton, M.; García-Braun, J. The influence of island-generated eddies on chlorophyll distribution: A study of mesoscale variation around Gran Canaria. Deep Sea Res. Part I Oceanogr. Res. Pap. 1997, 44, 71–96. [Google Scholar] [CrossRef]
- Salihoǧlu, İ.; Saydam, C.; Baştürk, Ö.; Yilmaz, K.; Göçmen, D.; Hatipoǧlu, E.; Yilmaz, A. Transport and distribution of nutrients and chlorophyll-a by mesoscale eddies in the northeastern Mediterranean. Mar. Chem. 1990, 29, 375–390. [Google Scholar] [CrossRef]
- Dufois, F.; Hardman-Mountford, N.J.; Fernandes, M.; Wojtasiewicz, B.; Shenoy, D.; Slawinski, D.; Gauns, M.; Greenwood, J.; Toresen, R. Observational insights into chlorophyll distributions of subtropical South Indian Ocean eddies. Geophys. Res. Lett. 2017, 44, 3255–3264. [Google Scholar] [CrossRef] [Green Version]
- Hajdu, S.; Höglander, H.; Larsson, U. Phytoplankton vertical distributions and composition in Baltic Sea cyanobacterial blooms. Harmful Algae 2007, 6, 189–205. [Google Scholar] [CrossRef]
- Dera, J.; Wozniak, B. Solar radiation in the Baltic Sea. Oceanologia 2010, 52, 533–582. [Google Scholar] [CrossRef]
- Simis, S.G.; Ylöstalo, P.; Kallio, K.Y.; Spilling, K.; Kutser, T. Contrasting seasonality in optical-biogeochemical properties of the Baltic Sea. PLoS ONE 2017, 12, e0173357. [Google Scholar] [CrossRef] [PubMed]
- Wozniak, B.; Dera, J. Light Absorption in Sea Water; Springer: New York, NY, USA, 2007; Volume 33, p. 463. [Google Scholar]
- Leibovich, S. On the evolution of the system of wind drift currents and Langmuir circulations in the ocean. Part 1. Theory and averaged current. J. Fluid Mech. 1977, 79, 715–743. [Google Scholar] [CrossRef]
- Global Drifter Program. Available online: https://www.aoml.noaa.gov/phod/gdp/index.php (accessed on 29 December 2021).
- Roemmich, D.; Argo Steering Team. Argo: The challenge of continuing 10 years of progress. Oceanography 2009, 22, 46–55. [Google Scholar] [CrossRef]
- de Souza, R.B.; Robinson, I.S. Lagrangian and satellite observations of the Brazilian Coastal Current. Cont. Shelf Res. 2004, 24, 241–262. [Google Scholar] [CrossRef]
- Krayushkin, E.; Lavrova, O.; Strochkov, A. Application of GPS/GSM Lagrangian mini-drifters for coastal ocean dynamics analysis. Russ. J. Earth Sci. 2019, 19, ES1001. [Google Scholar] [CrossRef] [Green Version]
- Sonnewald, M.; Lguensat, R.; Jones, D.C.; Dueben, P.; Brajard, J.; Balaji, V. Bridging observations, theory and numerical simulation of the ocean using machine learning. Environ. Res. Lett. 2021, 16, 073008. [Google Scholar] [CrossRef]









| Band | Wavelength (Landsat-8 OLI), nm | Wavelength (Sentinel 2A MSI), nm | <Vx>, cm/c | <Vy>, cm/c |
|---|---|---|---|---|
| Blue | 0.45–0.515 | 0.448–0.545 | −16.4 | −7.2 |
| Green | 0.525–0.6 | 0.537–0.582 | −14.9 | −7 |
| Red | 0.63–0.68 | 0.645–0.683 | −16.5 | −4.5 |
| NIR | 0.845–0.885 | 0.848–0.883 | −18.1 | −6.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shomina, O.; Danilicheva, O.; Tarasova, T.; Kapustin, I. Manifestation of Spiral Structures under the Action of Upper Ocean Currents. Remote Sens. 2022, 14, 1871. https://doi.org/10.3390/rs14081871
Shomina O, Danilicheva O, Tarasova T, Kapustin I. Manifestation of Spiral Structures under the Action of Upper Ocean Currents. Remote Sensing. 2022; 14(8):1871. https://doi.org/10.3390/rs14081871
Chicago/Turabian StyleShomina, Olga, Olga Danilicheva, Tatiana Tarasova, and Ivan Kapustin. 2022. "Manifestation of Spiral Structures under the Action of Upper Ocean Currents" Remote Sensing 14, no. 8: 1871. https://doi.org/10.3390/rs14081871
APA StyleShomina, O., Danilicheva, O., Tarasova, T., & Kapustin, I. (2022). Manifestation of Spiral Structures under the Action of Upper Ocean Currents. Remote Sensing, 14(8), 1871. https://doi.org/10.3390/rs14081871