A Characteristics Set Computation Model for Internal Wavenumber Spectra and Its Validation with MODIS Retrieved Parameters in the Sulu Sea and Celebes Sea

Abstract

The quasi-linear or nonlinear interactions among different ocean motions dominate the system internal structure and appearance feature presented in spatial and temporal evolution. However, deficiency of the characteristics set computation model for internal wavenumber spectra proves to be a serious barrier to derive interaction mechanisms of internal waves with large or small scale ocean motions. In this study, a characteristics set computation model for internal wavenumber spectra is proposed for complicated offshore environments. The refraction of current shear instability, bottom topography and the reflection at surface and bottom are attentively considered in the complicated characteristics inlaid scheme. Model results are validated with MODIS retrieved internal wave parameters in the Sulu Sea and Celebes Sea. This original characteristics set computation model for internal wavenumber spectra can be used widely and can further improve the understandings of generation, dissipation, nonlinear wave-wave interaction and mixing process of internal waves.

1. Introduction

The quasi-linear or nonlinear interactions in the ocean dynamic system dominate the physics of internal gravity waves [1,2,3]. The energy spectrum method is a practical and efficient way to interpret the internal wave composition structure and appearance properties. However, deficiency of the characteristics set computation model for internal wavenumber spectra proves to be a serious barrier to analyze interaction mechanisms of internal waves with large or small scale ocean motions. In fact, the characteristics/ray theory has been studied and successfully applied to the spectral propagation of surface waves [4,5,6,7]. It is probable to deeply recognize the horizontal anisotropy, high nonlinearity, spectrum denaturation of internal waves in the offshore if we follow the quite similar treatment of surface waves through the internal wave characteristics set modeling, which can interpret further the propagation physics of internal waves compared to the traditional models based on the primitive Navier–Stokes or KdV equations. Furthermore, satellite imagery can detect packets of internal waves which are common features propagating in the seas [1,8]. These satellite retrieved internal wave parameters (e.g., wavelength, phase velocity, etc.) are useful particularly and expediently to validate the field distributions obtained from the wave characteristics set modeling.

The internal waves appear in the satellite imagery as alternating bands of light and dark strips that result from sea surface roughness variations, which are due to the creation of convergent (rough) and divergent (smooth) zones set up by the internal wave currents that move across the surface in phase with wave’s subsurface crests and troughs [9,10]. MODIS (Moderate Resolution Imaging Spectroradiometer), SAR (Synthetic Aperture Radar) and other sensors on board satellites have the capabilities for large area detection of internal waves in their wide swath modes. The internal wave parameters can be obtained directly by using pairs of satellite images separated in time by only a few minutes to a few hours, or retrieved through the TMI (Tidal Period Images) method for application to the internal wave field studies [11]. In this study, we will apply the MODIS retrieved internal wave parameters to verify the proposed characteristics set computation model.

This paper is organized as follows. A derivation of the characteristics set computation model is given in Section 2.1. Ocean data related to the MODIS sensors and varying environmental modeled data from a wave-tide-circulation coupled model are described in Section 2.2. The applied results of the characteristics set computation model are presented in Section 3. Finally, a discussion and conclusions are presented in Section 4 and Section 5.

2. Materials and Methods

2.1. Model Derivation and Set-Up

2.1.1. Derivation of Internal Wave Energy Spectrum Balance Equation

In the usual notation, let $x_i,i=1,2,3$ be rectangular co-ordinates. Let $u_{SMi},i=1,2,3$ denote the internal wave velocities; $T_{SM},s_{SM},p_{SM},{\rho }_{SM}$ the perturbations of temperature, salinity, pressure and density induced by internal ocean waves. More comprehensive governing equations for wave motion were derived in Yuan et al. [3] and Yang et al. [12] and the unit volume wave energy balance equation can be obtained in tensor expression as follows:

$$\begin{array}{l}\frac{\partial }{\partial t}{〈\frac{{\rho }_0{u}_{SMi}^2}{2}+\frac{g^2{\rho }_{SM}^2}{2{\rho }_0{\widehat{N}}_3^2}〉}_{SM}+{〈\left({\widehat{U}}_j+u_{SMj}\right)\frac{\partial }{\partial x_j}\left(\frac{{\rho }_0{u}_{SMi}^2}{2}+\frac{g^2{\rho }_{SM}^2}{2{\rho }_0{\widehat{N}}_3^2}\right)〉}_{SM}+\frac{\partial }{\partial x_i}{〈p_{SM}{u}_{SMi}〉}_{SM}\\ =\left(-{\rho }_0{〈u_{SMi}{u}_{SMj}〉}_{SM}\frac{\partial {\widehat{U}}_i}{\partial x_j}+g{〈{\rho }_{SM}{u}_{SM\alpha }〉}_{SM}\frac{{\widehat{N}}_{\alpha }^2}{{\widehat{N}}_3^2}\right)+\frac{g^2}{{\rho }_0{\widehat{N}}_3^2}{〈{\rho }_{SM}{Q}_{\rho SM}〉}_{SM},\\ +\left\{\begin{array}{l}\frac{\partial }{\partial x_j}{〈\overline{\left({\nu }_0+\frac{k^2}{{\pi }^2\epsilon }\right)}\frac{\partial }{\partial x_j}\left(\frac{{\rho }_0{u}_{SMi}^2}{2}\right)〉}_{SM}+\frac{\partial }{\partial x_j}{〈\overline{\left(K_0+\frac{1}{{\sigma }_0}\frac{k^2}{{\pi }^2\epsilon }\right)}\frac{\partial }{\partial x_j}\left(\frac{g^2{\rho }_{SM}^2}{2{\rho }_0{\widehat{N}}_3^2}\right)〉}_{SM}\\ -{〈{\rho }_0\overline{\left({\nu }_0+\frac{k^2}{{\pi }^2\epsilon }\right)}{\left(\frac{\partial u_{SMi}}{\partial x_j}\right)}^2〉}_{SM}-{〈\frac{g^2}{{\rho }_0{\widehat{N}}_3^2}\overline{\left(K_0+\frac{1}{{\sigma }_0}\frac{k^2}{{\pi }^2\epsilon }\right)}{\left(\frac{\partial {\rho }_{SM}}{\partial x_j}\right)}^2〉}_{SM}\end{array}\right\}\end{array}$$

(1)

where ${\widehat{U}}_i,i=1,2,3;\widehat{T},\widehat{s},\widehat{p},\widehat{\rho }$ denote the background current components and ${\rho }_0$ is the basin mean water density; ${\nu }_0,{\kappa }_0,D_0$ the molecular viscosity, thermal and diffusion coefficients; ${\widehat{N}}_i^2=-g\frac{\partial }{\partial x_i}\left(\frac{\widehat{\rho }}{{\rho }_0}\right),i=1,2,3$ the Brunt–Väisälä frequency components; $k^2,\epsilon$ the kinetic energy and its dissipation rate of ocean turbulence, which is mainly generated by surface waves in the upper layers [13,14,15]. $\frac{{\rho }_0{u}_{SMi}^2}{2},\frac{g^2{\rho }_{SM}^2}{2{\rho }_0{\widehat{N}}_3^2}$ denote the kinetic and potential internal wave energy and $〈\cdot {〉}_{SM}$ denotes the Reynolds average in wave motion. Otherwise the notation is standard. The first term on the left-hand side of Equation (1) is related to the local mechanical energy variation and the second and third ones denote the energy flux transferred by internal waves and background currents. The first and second terms on the right-hand side of Equation (1) are related to the modulation by larger scale motions through shear instability generations. The third term is related to the energy input through thermal radiation, the fourth and fifth ones are related to the modulation by smaller scale motions through ocean mixing and the last two terms are related to the energy loss rate due to internal viscosity.

Let $E\left(\stackrel{\rightharpoonup }{k}\right)\hspace{0.17em}=E\left(k_1,k_2,k_3\right)$ designate an internal wavenumber energy spectrum for unit mass water, i.e.,

$$\frac{1}{{\rho }_0}{〈\frac{{\rho }_0\left(u_{SMi}{u}_{SMi}\right)}{2}+\frac{g^2{\rho }_{SM}^2}{2{\rho }_0{\widehat{N}}_3^2}〉}_{SM}={\displaystyle \underset{\stackrel{\rightharpoonup }{K}}{\iiint }E\left(\stackrel{\rightharpoonup }{k}\right)\hspace{0.17em}d{k}_{1}d{k}_{2}d{k}_3},$$

(2)

and the corresponding wave energy balance equation can be written as:

$${\displaystyle \underset{\stackrel{\rightharpoonup }{K}}{\iiint }\left\{\frac{\partial E\left(\stackrel{\rightharpoonup }{k}\right)}{\partial t}+\left[{\widehat{U}}_i+C_{gi}\right]\frac{\partial E\left(\stackrel{\rightharpoonup }{k}\right)}{\partial x_i}-\left[S_{CU}\left(\stackrel{\rightharpoonup }{k}\right)+S_{FR}\left(\stackrel{\rightharpoonup }{k}\right)+S_{ED}\left(\stackrel{\rightharpoonup }{k}\right)-S_{DS}\left(\stackrel{\rightharpoonup }{k}\right)\right]\right\}\hspace{0.17em}d{k}_{1}d{k}_{2}d{k}_3=0}\hspace{0.17em},$$

(3)

where $C_{gi},i=1,2,3$ denote the wave group velocities, which can be derived by internal wave frequency dispersion relations which will be discussed in detail in Section 2.1.2 and Section 3.1. $S_{CU}\left(\stackrel{\rightharpoonup }{k}\right),S_{FR}\left(\stackrel{\rightharpoonup }{k}\right),S_{ED}\left(\stackrel{\rightharpoonup }{k}\right)$ and $S_{DS}\left(\stackrel{\rightharpoonup }{k}\right)$ are related to wave-current, wave-water stratification, wave-thermal radiation and dissipation terms. Equation (3) indicates that the integrand function performs the energy transfer behavior due to nonlinear wave-wave interaction $S_{NL}\left(\stackrel{\rightharpoonup }{k}\right)$, whose integral is zero in wave-number space. i.e.,

$$\frac{\partial E\left(\stackrel{\rightharpoonup }{k}\right)}{\partial t}+\left[{\widehat{U}}_i+C_{gi}\right]\frac{\partial E\left(\stackrel{\rightharpoonup }{k}\right)}{\partial x_i}-\left[S_{CU}\left(\stackrel{\rightharpoonup }{k}\right)+S_{FR}\left(\stackrel{\rightharpoonup }{k}\right)+S_{ED}\left(\stackrel{\rightharpoonup }{k}\right)-S_{DS}\left(\stackrel{\rightharpoonup }{k}\right)\right]=S_{NL}\left(\stackrel{\rightharpoonup }{k}\right),$$

(4)

Correspondingly,

$$\begin{array}{l}\frac{\partial E\left(\stackrel{\rightharpoonup }{k}\right)}{\partial t}+\left[{\widehat{U}}_i+C_{gi}\right]\frac{\partial E\left(\stackrel{\rightharpoonup }{k}\right)}{\partial x_i} =S_{NL}\left(\stackrel{\rightharpoonup }{k}\right)+S_{CU}\left(\stackrel{\rightharpoonup }{k}\right)+S_{FR}\left(\stackrel{\rightharpoonup }{k}\right)+S_{ED}\left( \stackrel{\rightharpoonup }{k}\right)-S_{DS}\left(\stackrel{\rightharpoonup }{k}\right)\\ \begin{array}{ccccccccc}& & & & & & & & =\end{array}SS\left(\stackrel{\rightharpoonup }{k}\right)\end{array}$$

(5)

There are also other boundary input source functions, such as the wind and surface gravity wave energy input terms not included here. In this study, we are concerned entirely with the propagation properties of wave-number spectrum, so we let $SS\left(\stackrel{\rightharpoonup }{k}\right)\equiv 0$ for further numerical modeling performed below.

2.1.2. 3-Dimensional Complicated Characteristics Set Equations

In the preceding derivations, we implicitly assume the horizontal invariance of density, topography, etc., as in Yuan et al. [2]; the complex frequency–wavenumber relation at the sea surface can be simplified as:

$${\omega }^2=f^2+\frac{1}{{\mu }_{IW}(0)}\cdot g\frac{{\widehat{\rho }}_0}{{\rho }_0}{k}_H\tan ({\displaystyle {\int }_{-{\widehat{H}}_N}^0{\mu }_{IW}{k}_{H}d{x}_3}),$$

(6)

where f denotes the Coriolis parameter; ${\widehat{H}}_N$ represents the depth where $\omega ={\widehat{N}}_3$ (it is also called a reflection level where the wave frequency matches the background buoyancy frequency). If $\omega <{\widehat{N}}_3$ from surface to bottom, then ${\widehat{H}}_N=\widehat{H}$. And:

$${\mu }_{IW}=\sqrt{\frac{{\widehat{N}}_3^2-{\omega }^2}{{\omega }^2-f^2}},{\mu }_{IW}(0)=\sqrt{\frac{{\widehat{N}}_{30}^2-{\omega }^2}{{\omega }^2-f^2}},{\widehat{N}}_{30}^2=-g\frac{\partial }{\partial x_3}{\left.(\frac{\widehat{\rho }}{{\rho }_0})\right|}_{x_3=0},{\widehat{\rho }}_0={\left.\widehat{\rho }\right|}_{x_3=0},$$

(7)

$$k_H^2=k_1{}^2+k_2^2,k^2=k_H^2+k_3^2,$$

(8)

Equation (6) can also be practically expressed as:

$${\displaystyle {\int }_{-{\widehat{H}}_N}^0{k}_{3}d{x}_3}=i\pi +\arctan (\frac{{\rho }_0}{{\widehat{\rho }}_0}\frac{\sqrt{({\widehat{N}}_{30}^2-{\omega }^2)({\omega }^2-f^2)}}{g{k}_H}),\begin{array}{cc}& i=1,2,\dots \end{array},$$

(9)

where $i=1,2,\dots$ denote the vertical mode numbers of internal gravity waves.

The vertical wavenumber $k_3$ satisfies:

$$k_3^2=\frac{{\widehat{N}}_3^2-{\omega }^2}{{\omega }^2-f^2}{k}_H^2,$$

(10)

or

$${\omega }^2=\frac{{\widehat{N}}_3^2{k}_H^2+f^2{k}_3^2}{k^2},$$

(11)

So the group velocities can be obtained as:

$$\left\{\begin{array}{l}{C}_{g1}=\frac{\partial \omega }{\partial k_1}=\frac{{\widehat{N}}_3^2-{\omega }^2}{\omega k^2}{k}_1\\ C_{g2}=\frac{\partial \omega }{\partial k_2}=\frac{{\widehat{N}}_3^2-{\omega }^2}{\omega k^2}{k}_2\\ C_{g3}=\frac{\partial \omega }{\partial k_3}=-\frac{{\omega }^2-f^2}{\omega k^2}{k}_3\end{array}\right.,$$

(12)

The ray method or characteristics method is valid for a study of both linear and nonlinear wave packets propagating both in homogeneous and inhomogeneous media [4,5,16,17]. Here we present the practical characteristics equations for further interpreting the refraction induced by topography and current. The characteristics equation describes the propagation law of ocean waves in physical space and it can be written as:

$$\frac{d{x}_i}{dt}=C_{gi}+{\widehat{U}}_i\begin{array}{cc},& \end{array}(i=1,2,3),$$

(13)

By using the motion equations of waves,

$$\begin{array}{l}\frac{\partial k_i}{\partial x_j}=\frac{\partial k_j}{\partial x_i}\begin{array}{cc}& \end{array}(i\ne j;i,j=1,2,3)\\ \frac{\partial k_i}{\partial t}+\frac{\partial \sigma }{\partial x_i}=0\begin{array}{cc}& \end{array}(i=1,2,3)\end{array}$$

(14)

with $\sigma =\omega +k_i\cdot {\widehat{U}}_i$, after some manipulation, the variation laws of the modulus and azimuth angles of wavenumber can be derived as:

$$\frac{\partial \theta }{\partial t}+(C_{gi}+{\widehat{U}}_i)\frac{\partial \theta }{\partial x_i}=-\frac{1}{k_H}\left[\frac{\partial \omega }{\partial \widehat{H}}\frac{\partial \widehat{H}}{\partial x_{\alpha }}{n}_{\alpha }+k_i\frac{\partial {\widehat{U}}_i}{\partial x_{\alpha }}{n}_{\alpha }\right],$$

(15)

$$\frac{\partial k}{\partial t}+(C_{gi}+{\widehat{U}}_i)\frac{\partial k}{\partial x_i}=-\left[\frac{\partial \omega }{\partial \widehat{H}}\frac{\partial \widehat{H}}{\partial x_{\alpha }}{s}_{2\alpha }+k_i\frac{\partial {\widehat{U}}_i}{\partial x_j}{s}_{3j}\right],$$

(16)

$$\frac{\partial \phi }{\partial t}+(C_{gi}+{\widehat{U}}_i)\frac{\partial \phi }{\partial x_i}=-\frac{1}{k}\left[\frac{\partial \omega }{\partial \widehat{H}}\frac{\partial \widehat{H}}{\partial x_{\alpha }}{n}_{2\alpha }+k_i\frac{\partial {\widehat{U}}_i}{\partial x_j}{n}_{3j}\right],$$

(17)

where $\alpha =1,2;i,j=1,2,3$, $k_1=k_H\cos \theta ,k_2=k_H\sin \theta$ and $k_H=k\cos \phi ,k_3=k\sin \phi$. Angle $\theta$ rotates anticlockwise and is 0° in the east direction in the following numerical experiments. Normalized vectors in Equations (15)–(17) are defined as follows:

$$\begin{array}{l}\stackrel{\rightharpoonup }{s}=(\cos \theta ,\sin \theta ),\stackrel{\rightharpoonup }{n}=(-\sin \theta ,\cos \theta ),\\ {\stackrel{\rightharpoonup }{s}}_2=(\cos \phi \cos \theta ,\cos \phi \sin \theta ),{\stackrel{\rightharpoonup }{n}}_2=(-\sin \phi \cos \theta ,-\sin \phi \sin \theta ),\\ {\stackrel{\rightharpoonup }{s}}_3=(\cos \phi \cos \theta ,\cos \phi \sin \theta ,\sin \phi ),{\stackrel{\rightharpoonup }{n}}_3=(-\sin \phi \cos \theta ,-\sin \phi \sin \theta ,\cos \phi ).\end{array}$$

(18)

Differentiated by $\widehat{H}$ in both sides of Equation (9), we obtain:

$$\frac{\partial \omega }{\partial \widehat{H}}=\left\{\begin{array}{l}\frac{{\widehat{\rho }}_0}{{\rho }_0}\frac{{\omega }_{N_0}^2\left[g^2{k}_H^2+{\left(\frac{{\rho }_0}{{\widehat{\rho }}_0}\right)}^2{\left({\omega }_{N_0}^2\right)}^2\right]}{g\omega k_H\left({\widehat{N}}_{30}^2+f^2-2{\omega }^2\right)}\cdot {\left.k_3\right|}_{x_3=-{\widehat{H}}_N}\begin{array}{cc},& {\widehat{H}}_N=\widehat{H}\end{array}\\ 0,\begin{array}{cccc}& & & \begin{array}{cccc}& & & \begin{array}{cccc}& & & \begin{array}{ccccccccccc}& & & & & & & & & & {\widehat{H}}_N<\widehat{H}\end{array}\end{array}\end{array}\end{array}\end{array}\right.,$$

(19)

where ${\omega }_{N_0}^2=\sqrt{({\widehat{N}}_{30}^2-{\omega }^2)({\omega }^2-f^2)}$. Equations (13) and (15)–(17) in the unknowns $x_i\left(i=1,2,3\right),k,\theta ,\phi$ are the 3-dimensional complicated characteristics set equations which are effectively applied to the propagation experiments performed below. These equations describe the effects of spatially varying bottom depth and current on the wave propagation, which includes the refraction of current shear instability and bottom topography and the modulation by current through advection transport.

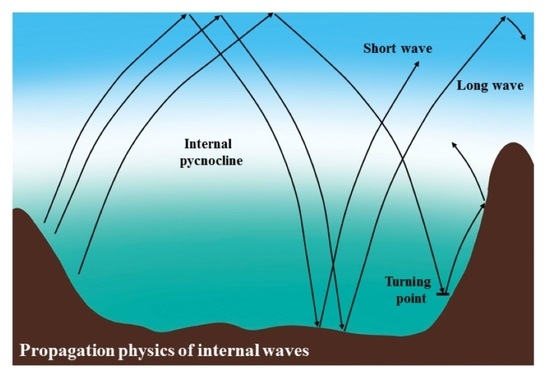
2.1.3. Reflection at the Surface and Bottom

The characteristics or ray theory predicts that internal waves reflect at surface or at the reflection level ${\widehat{H}}_N$ which is supposed as ${\widehat{H}}_N=\widehat{H}$ below. The boundary condition of equations of internal wave motion at bottom is [2]:

$${\left(u_{SM3}\right)}_{x_3=-\widehat{H}}+\frac{\partial \widehat{H}}{\partial x_{\alpha }}{\left(u_{SM\alpha }\right)}_{x_3=-\widehat{H}}=0,$$

(20)

Further, ${\stackrel{\rightharpoonup }{n}}_{up}=\left(\frac{\partial \widehat{H}}{\partial x_1},\frac{\partial \widehat{H}}{\partial x_2},1\right)$ denotes the upward normal vector at bottom. The incident, reflected wavenumbers $\stackrel{\rightharpoonup }{k}=(k_1,k_2,k_3),\stackrel{\rightharpoonup }{l}=(l_1,l_2,l_3)$ and the reflection coefficient A satisfy the conservation laws of kinematics [18] and we obtain:

$$l_H=\frac{1\pm {\mu }_{IW}(\frac{\partial \widehat{H}}{\partial x_1}\cos \theta +\frac{\partial \widehat{H}}{\partial x_2}\sin \theta )}{1\mp {\mu }_{IW}(\frac{\partial \widehat{H}}{\partial x_1}\cos \theta +\frac{\partial \widehat{H}}{\partial x_2}\sin \theta )}{k}_H,$$

(21)

$$l_3=-\frac{1\pm {\mu }_{IW}(\frac{\partial \widehat{H}}{\partial x_1}\cos \theta +\frac{\partial \widehat{H}}{\partial x_2}\sin \theta )}{1\mp {\mu }_{IW}(\frac{\partial \widehat{H}}{\partial x_1}\cos \theta +\frac{\partial \widehat{H}}{\partial x_2}\sin \theta )}{k}_3,$$

(22)

$$A=-\frac{1\pm {\mu }_{IW}(\frac{\partial \widehat{H}}{\partial x_1}\cos \theta +\frac{\partial \widehat{H}}{\partial x_2}\sin \theta )}{1\mp {\mu }_{IW}(\frac{\partial \widehat{H}}{\partial x_1}\cos \theta +\frac{\partial \widehat{H}}{\partial x_2}\sin \theta )},$$

(23)

corresponding to $k_3=-{\mu }_{IW}{k}_H,l_3={\mu }_{IW}{l}_H$ or $k_3={\mu }_{IW}{k}_H,l_3=-{\mu }_{IW}{l}_H$, respectively. According to rigid surface assumption, Equations (21)–(23) can be simplified as:

$$l_H=k_H,\begin{array}{cc}& l_3=-k_3\end{array},\begin{array}{cc}& A=-1\end{array},$$

(24)

The reflected wave satisfies ${\stackrel{\rightharpoonup }{C}}_g\cdot {\stackrel{\rightharpoonup }{n}}_{up}>0$ at bottom. By employing Equation (12), it yields:

$$({\widehat{N}}_3^2-{\omega }^2)l_1\frac{\partial \widehat{H}}{\partial x_1}+({\widehat{N}}_3^2-{\omega }^2)l_2\frac{\partial \widehat{H}}{\partial x_2}-({\omega }^2-f^2)l_3>0,$$

(25)

So that in numerical modeling, Formula (25) can be seemed as a criterion if the discrete wavenumber is a reflected one or not. Moreover, at surface, Formula (25) is simplified as $l_3>0$. Consequently, the discrete reflected wavenumber spectrum roughly satisfies:

$$E\left(l_1,l_2,l_3\right)\hspace{0.17em}=A^{2}E\left(k_1,k_2,k_3\right),$$

(26)

where the incident wavenumber may be not the discrete one and its spectrum $E\left(k_1,k_2,k_3\right)$ is 3-dimensionally and linearly interpolated among the adjacent eight discrete wavenumbers in the phase space.

2.1.4. Grid Distribution and Complicated Characteristics Inlaid Scheme in Physical and Phase Spaces

In physical space, we take the horizontal grid parallel to the longitude and latitude lines in the study domain with the resolution of 1°/3 by 1°/3 or 1°/6 by 1°/6 and the uniform vertical grid spacing of 20 m. The maximum water depth is set to 3000 m. Figure 1 is our model computational domain and bathymetry.

In wavenumber space, we take polar coordinate grids according to the proposed negative exponential form of empirical internal wavenumber spectrum $\mathrm{E}\left(\mathrm{k}\right)~{\mathrm{k}}^{-\mathsf{\beta }}$, i.e.,

$${\mathrm{k}}_{\mathrm{i}}={\mathrm{k}}_{\min }{\mathrm{e}}^{\left(\mathrm{i}-1\right)·∆\mathrm{k}}, \mathrm{i}=1,2,\dots ,\mathrm{K}+1, \mathrm{where} ∆\mathrm{k}=\frac{1}{\mathrm{K}}\log \left(\frac{{\mathrm{k}}_{\max }}{{\mathrm{k}}_{\min }}\right)$$

(27)

The horizontal and vertical angles of wave direction are discretized uniformly below:

$${\mathsf{\theta }}_{\mathrm{i}}=\left(\mathrm{i}-1\right)·∆\mathsf{\theta }, \mathrm{i}=1,2,\dots ,\mathrm{N}+1, \mathrm{where} ∆\mathsf{\theta }=\frac{2\mathsf{\pi }}{\mathrm{N}}$$

(28)

$${\mathsf{\phi }}_{\mathrm{i}}=-\frac{\mathsf{\pi }}{2}+\frac{∆\mathsf{\phi }}{2}+\left(\mathrm{i}-1\right)∆·\mathsf{\phi }, \mathrm{i}=1,2,\dots ,\mathrm{M}, \mathrm{where} ∆\mathsf{\phi }=\frac{\mathsf{\pi }}{\mathrm{M}}$$

(29)

The above model settings can be modified according to different requirements. The complicated characteristics inlaid scheme is designed as Figure 2.

2.2. Ocean Data

2.2.1. MODIS Data

The MODIS sensors are onboard the National Aeronautics and Space Administration’s (NASA’s) Earth Observing System satellites Terra and Aqua. The MODIS data have a spatial resolution between 250 m and 1 km, dependent on the collection wavelength [19] and with a geolocation accuracy of at least 60 m (1σ) [20]. Full details of the characteristics of MODIS and its associated data products are given on the NASA MODIS website (modis.gsfc.nasa.gov, accessed on 30 November 2021). Previous studies have been done on the inversion mechanisms of internal waves from satellite data [8,9,10,21,22,23]. Here in this study, the Aqua-MODIS images with a spatial resolution of 250 m are used to retrieve the internal wavelengths, here defined as the distance between two successive wave packets and the corresponding apparent phase velocities.

2.2.2. Modeled Data

The modeled data were presented by using the Key Laboratory of Marine Science and Numerical Modeling (MASNUM) wave-tide-circulation coupled model [24], which employs the MASNUM wavenumber spectral model [6,7] and the POM circulation model [25]. The key mixing role induced by surface waves in the formation of upper mixed layer [15,26,27,28] was considered in the coupled model. The coupled model covers the computational domain (10° S–30°N, 90–135°E) with the horizontal resolution of 1°/30 by 1°/30 and the vertical 51 sigma layers. The model was integrated for 10 years and the gridded products of SSH anomaly, circulation pattern, subsurface temperature, etc., were validated to the satellite altimetry and in situ observations [24]. The simulated climatological monthly-mean temperature, salinity, etc., of year 10 are used in this study.

3. Results

3.1. Validation

3.1.1. Simplified Wave Frequency Dispersion Relations

The vertical mean wavenumber $\overline{k}={\left({\overline{k}}_H^2+{\overline{k}}_3^2\right)}^{1/2}$ can be obtained through a non-trivial iteration scheme according to Equation (9) and the following transformation of Equation (10):

$${\displaystyle {\int }_{-{\widehat{H}}_N}^0{k}_{3}d{x}_3}={\displaystyle {\int }_{-{\widehat{H}}_N}^0\left(\sqrt{\frac{{\widehat{N}}_3^2-f^2}{{\omega }^2-f^2}-1}\right)k_{H}d{x}_3={\overline{k}}_H{\displaystyle {\int }_{-{\widehat{H}}_N}^0\left(\sqrt{\frac{{\widehat{N}}_3^2-f^2}{{\omega }^2-f^2}-1}\right)d{x}_3}},$$

(30)

The vertical integration of Equations (9) and (30) constitute the simplified wave frequency dispersion relations. As the result of introducing the vertical mean group velocity, according to Equation (12), it can be expressed as follows:

$${\stackrel{\rightharpoonup }{C}}_g=({\overline{C}}_{gH},{\overline{C}}_{g3})=\left(\frac{(\frac{1}{{\widehat{H}}_N}{\displaystyle {\int }_{-{\widehat{H}}_N}^0\sqrt{{\widehat{N}}_3^2-{\omega }^2}d{x}_3{)}^2}}{\omega {\overline{k}}^2}{\overline{k}}_H,-\frac{{\omega }^2-f^2}{\omega {\overline{k}}^2}{\overline{k}}_3\right),$$

(31)

Obviously, the phase velocity $\stackrel{\rightharpoonup }{C}=\left({\overline{C}}_H,{\overline{C}}_3\right)=\left(\frac{\omega }{\overline{k}}\frac{{\overline{k}}_H}{\overline{k}},\frac{\omega }{\overline{k}}\frac{{\overline{k}}_3}{\overline{k}}\right)$ and the above group velocity also satisfy $\stackrel{\rightharpoonup }{C}\cdot {\stackrel{\rightharpoonup }{C}}_g=0$ in accordance with the classical theories. The horizontal apparent wavelength and phase velocity are defined as ${\lambda }_H^{ap}=\frac{2\pi }{{\overline{k}}_H},{\overline{C}}_H^{ap}=\frac{\omega }{{\overline{k}}_H}$, which will be calculated and compared with MODIS retrieved ones for semidiurnal internal tide with the period of 12.42 h in the Sulu Sea and Celebes Sea.

3.1.2. MODIS Retrieved Parameters and Comparison with Modeled Results

The MODIS survey identified significant internal wave activity in the Sulu and Celebes Seas. Figure 3 is the Aqua-MODIS image acquired on 10 October 2018 at 5:20–5:25 UTC that shows internal wave signatures originated in (or near) the Sulu Archipelago, with 5 groups of wave packets propagating across the Sulu Sea to the northwest and 4 groups propagating across the Celebes Sea to the southeast. The apparent phase velocity can be retrieved through the TMI (Tidal Period Images) method [11] based on the distance between two successive wave packets, which can be obtained directly from the image. The mean velocities are 2.26, 2.88 m/s in the Sulu Sea and Celebes Sea, respectively. The corresponding retrieved parameters to wave packets are listed in

Table 1. MODIS retrieved parameters compared to modeled ones in the Sulu Sea and Celebes Sea.

Area	Internal Waves	First Crest Line Length (km)	Wavelength (km)		Apparent Phase Velocity (m/s)
			MODIS	Model	MODIS	Model
Sulu Sea	Packet 1	126.79	102.14	52.03	2.28	1.17
	Packet 2	173.12	104.97	122.90	2.35	2.75
	Packet 3	210.11	99.34	84.49	2.22	1.89
	Packet 4	263.93	97.34	119.10	2.17	2.67
	Packet 5	367.38	-		-
Celebes Sea	ISW 1	57.94	121.40	139.80	2.71	3.13
	ISW 2	251.83	140.81	159.50	3.15	3.57
	ISW 3	316.84	124.62	137.20	2.79	3.08
	ISW 4	248.71	-		-

.

Figure 4a–c show the modeled horizontal wavelength ${\lambda }_H^{ap}$ for mode 1, 2 and 3 of semidiurnal internal tide, in which the subgraph colorbar is different for clarity. It indicates that the wavelength of mode 2 agrees well with the MODIS retrieved ones, while the other two are too larger or smaller. In Figure 4b, the spatial distribution of wavelength is homogenous in the Celebes Sea with the quantity of approximately 140 km, but varies much in the Sulu Sea from 70 km to 140 km. It is evident that this responds to the varied terrain, especially in the shallow water area. Figure 5 shows the modeled phase velocity ${\overline{C}}_H^{ap}$ of mode 2 in the Sulu Sea and Celebes Sea. Similarly, it varies from 1.8 m/s to 3.0 m/s in the northwestern Sulu Sea and reaches up to 3.4 m in the central and eastern region, which is a little larger than the MODIS retrieved ones listed in Table 1. However, in most of the Celebes Sea, it has a uniform velocity of approximately 3.0 m/s, which agrees well with the MODIS retrieved ones. The modeled wavelength and phase velocity of mode 2 are also listed in Table 1 near the corresponding locations of MODIS observations. Both are relatively consistent except for Packet 1 in the Sulu Sea, which is mainly due to the varied terrain in the offshore area with coarse resolution of our model.

The modeled group velocity ${\overline{C}}_{gH}$ of mode 2 in the Sulu Sea and Celebes Sea is also calculated and distributed in Figure 6, which has similar properties as the phase velocity interpreted above. Its characteristic scale is about 2.0–3.5 m/s for semidiurnal internal tide in deep water area. Three-dimensional group velocity plays a key role in the propagation of internal wavenumber spectrum, which will be discussed below.

3.2. Analysis of Spectral Propagation

We wish to explore the internal wave spatial propagation behavior; the integral of internal wavenumber spectrum at any depth layer is presented for further conveniently interpreting, i.e., $\overline{E}={\displaystyle \underset{\stackrel{\rightharpoonup }{K}}{\iiint }E\left(\stackrel{\rightharpoonup }{k}\right)\hspace{0.17em}d{k}_{1}d{k}_{2}d{k}_3}$ and the three-dimensional unit vector of spectral mean wave direction is defined as:

$${\stackrel{\rightharpoonup }{V}}_{wd}=\left(\frac{1}{\overline{E}}{\displaystyle \underset{\stackrel{\rightharpoonup }{K}}{\iiint }E\left(\stackrel{\rightharpoonup }{k}\right)\hspace{0.17em}\cos \phi \cos \theta d{k}_{1}d{k}_{2}d{k}_3},\frac{1}{\overline{E}}{\displaystyle \underset{\stackrel{\rightharpoonup }{K}}{\iiint }E\left(\stackrel{\rightharpoonup }{k}\right)\hspace{0.17em}\cos \phi \sin \theta d{k}_{1}d{k}_{2}d{k}_3},\frac{1}{\overline{E}}{\displaystyle \underset{\stackrel{\rightharpoonup }{K}}{\iiint }E\left(\stackrel{\rightharpoonup }{k}\right)\hspace{0.17em}\sin \phi d{k}_{1}d{k}_{2}d{k}_3}\right)$$

(32)

In order to examine the applicability of the characteristics set computation model stated above, the initial GM75 spectrum [29] is set radially in the Sulu Archipelago with two major directions, northwest to the Sulu Sea and southeast to the Celebes Sea. The spectral propagation can be considered and reduced to the following two successive stages: P1 and P2: During the first stage P1, the wavenumber spectrum mainly propagates vertically with the low horizontal group velocity near the Sulu Archipelago, but reflects at surface and bottom frequently, so the mean wave direction appears as much scattering (Figure 7). During the second stage P2, the wavenumber spectrum propagates thoroughly across the deep water area in the Sulu Sea and Celebes Sea; besides reflecting at surface and bottom, the mean wave direction concentrates in an orderly manner (Figure 8). Furthermore, the refraction of bottom topography considered in Equations (15)–(17) and (19) plays a perceptible role in the western and eastern offshore areas of the Sulu Sea and the western offshore area of the Celebes Sea. Figure 8b indicates that internal waves also propagate affluently to the northeast in the Sulu Sea, as has previously been found from satellite observations [30,31]. However, the western propagating waves detected by [8] are not simulated here in the Celebes Sea, which needs to be further studied in the future.

4. Discussion

Fine resolution, large swath MODIS or SAR imagery has the ability to survey the properties of internal wave field evolution and applicability to interpret and verify the inherent dynamic mechanisms of wavenumber spectral propagation. The complicated characteristics inlaid scheme is an efficient way to simulate the internal wave propagation. In this study, a characteristics set computation model for internal wavenumber spectra is proposed for complicated offshore environments. The refraction of current shear instability, bottom topography and the reflection at surface and bottom were tentatively considered in the computational scheme. A rather cautious derivation was employed for the interaction dynamics which dominates the wave internal and external properties. However, there are still other processes, such as the enhancement near the turning depth or latitude [32,33,34] which are not considered here, which will be studied later.

Model grid discretization and computational configuration were designed for numerical experiments in the Sulu Sea and Celebes Sea. The modeled horizontal wavelength ${\lambda }_H^{ap}$ and phase velocity ${\overline{C}}_H^{ap}$ for mode 2 of semidiurnal internal tide agree well with the MODIS retrieved ones. Spatial distributions indicate that these parameters vary much in the Sulu Sea but homogenously in the Celebes Sea, which is largely due to the former varied terrain in the northern offshore. In situ survey data are needed for further comparison with the modeled results.

Numerical spectral propagation experiments indicate that after the first distracting stage near the Sulu Archipelago, the waves propagate concentrately in an orderly manner in the deep water area, in which the reflection at surface and bottom plays an important role in long-range propagating and the refraction of bottom topography plays a perceptible role in the offshore areas. The internal waves also propagate affluently to the northeast in the Sulu Sea. These numerical results agree with the previous MODIS/SAR imagery identifications.

5. Conclusions

Packets of internal waves propagating in the seas are common features detected by large amounts of satellite imagery. A characteristics set computation model for internal wavenumber spectra is proposed for complicated offshore environments to interpret further the propagation physics of internal waves. The refraction of current shear instability, bottom topography and the reflection at surface and bottom are attentively considered in the complicated characteristics inlaid scheme. Theoretical analysis and numerical modeling were implemented in the Sulu Sea and Celebes Sea and evaluated with the MODIS retrieved internal wave parameters. The results suggest that the original characteristics set computation model for internal wave spectra can be used widely and will be helpful in improving the understandings of generation, dissipation, nonlinear wave-wave interaction and mixing process of internal waves.