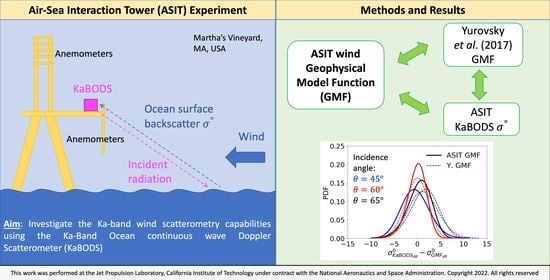
A Ka-Band Wind Geophysical Model Function Using Doppler Scatterometer Measurements from the Air-Sea Interaction Tower Experiment
Abstract
:1. Introduction
2. Materials and Methods
2.1. KaBODS Instrument Description
2.2. Meteorological and Oceanic Data Collection
2.3. KaBODS Signal Power Processing
2.4. The KaBODS Surface Backscatter Computation
2.5. Geophysical Model Function Development
3. Results
3.1. Wind Speed Sensitivity
3.2. Wind Direction Modulation
3.3. Model Accuracy
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| m | i | k | |
|---|---|---|---|
| 0 | 0 | 0 | |
| 1 | 0 | 0 | |
| 2 | 0 | 0 | |
| 3 | 0 | 0 | |
| 4 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 1 | 0 | |
| 2 | 1 | 0 | |
| 3 | 1 | 0 | |
| 4 | 1 | 0 | |
| 0 | 2 | 0 | |
| 1 | 2 | 0 | |
| 2 | 2 | 0 | |
| 3 | 2 | 0 | |
| 4 | 2 | 0 | |
| 0 | 0 | 1 | |
| 1 | 0 | 1 | |
| 2 | 0 | 1 | |
| 3 | 0 | 1 | |
| 4 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 1 | 1 | |
| 2 | 1 | 1 | |
| 3 | 1 | 1 | |
| 4 | 1 | 1 | |
| 0 | 2 | 1 | |
| 1 | 2 | 1 | |
| 2 | 2 | 1 | |
| 3 | 2 | 1 | |
| 4 | 2 | 1 |
References
- Ulaby, F.T.; Long, D.G. Radar Measurements and Scatterometers. In Microwave Radar and Radiometric Remote Sensing, 4th ed.; The University of Michigan Press: Ann Arbor, MI, USA, 2014; pp. 605–669. [Google Scholar]
- Valenzuela, G.R. Theories for the Interaction of Electromagnetic Waves and Oceanic Waves. A Review. Bound. Layer Met. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Hauser, D.; Caudal, G.; Chapron, B. A Semiempirical Model of the Normalized Radar Cross-Section of the Sea Surface 1. Background model. J. Geophys. Res. Oceans 2003, 108, C08054. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Stoffelen, A.; de Haan, S. An Improved C-band Scatterometer Ocean Geophysical Model Function: CMOD5. J. Geophys. Res. 2007, 12, 1–18. [Google Scholar] [CrossRef]
- Voronovich, A.G.; Zavorotny, V.U. Theoretical Model for Scattering of Radar Signals in Ku- and C-bands from a Rough Sea Surface with Breaking Waves. Waves Random Media 2001, 11, 247–269. [Google Scholar] [CrossRef]
- Plant, W.J. A stochastic Multiscale Model of Microwave Backscatter from the Ocean. J. Geophys. Res. 2002, 107, 3120. [Google Scholar] [CrossRef]
- Stoffelen, A.; Verspeek, J.; Vogelzang, J.; Verhoef, A. The CMOD7 Geophysical Model Function for ASCAT and ERS Wind Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2123–2134. [Google Scholar] [CrossRef]
- Ricciardulli, L.; Wentz, F.J. A Scatterometer Geophysical Model Function for Climate-quality Winds: QuikSCAT Ku-2011. J. Atmos. Ocean. Technol. 2015, 32, 1829–1846. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Meissner, T.; Cerovecki, I.; Chang, P.S.; Dong, X.; De Chiara, G.; Donlon, C.; Dukhovskoy, D.S.; Elya, J.; Fore, A.; et al. Remotely Sensed Winds and Wind Stresses for Marine Forecasting and Ocean Modeling. Front. Mar. Sci. 2010, 6, 443. [Google Scholar] [CrossRef] [Green Version]
- Shankaranarayanan, K.; Donelan, M.A. A Probabilistic Approach to Scatterometer Model Function Verification. J. Geophys. Res. Oceans 2001, 106, 19969–19990. [Google Scholar] [CrossRef] [Green Version]
- Portabella, M.; Stoffelen, A. Scatterometer Backscatter Uncertainty due to Wind Variability. IEEE Trans. Geosc. Remote Sens. 2006, 44, 3356–3362. [Google Scholar] [CrossRef]
- Vandemark, D.C.; Chapron, B.; Feng, H.; Mouche, A. Sea Surface Reflectivity Variation with Ocean Temperature at Ka-Band Observed Using Near-Nadir Satellite Radar Data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 510–514. [Google Scholar] [CrossRef]
- Wang, Z.; Stoffelen, A.; Zhao, C.; Vogelzang, J.; Verhoef, A.; Verspeek, J.; Lin, M.; Chen, G. SST-dependent Ku-band Geophysical Model Function for RapidScat. J. Geophys. Res. Ocean. 2017, 122, 3461–3480. [Google Scholar] [CrossRef]
- Wang, Z.; Stoffelen, A.; Fois, F.; Verhoef, A.; Zhao, C.; Lin, M.; Chen, G. SST Dependence of Ku- and C-band Backscatter Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2135–2146. [Google Scholar] [CrossRef]
- Rodríguez, E.; Bourassa, M.; Chelton, D.; Farrar, J.T.; Long, D.; Perkovic-Martin, D.; Samelson, R. The Winds and Currents Mission Concept. Front. Mar. Sci. 2019, 6, 438. [Google Scholar] [CrossRef]
- Martz, H.E., Jr.; McNeil, B.J.; Amundson, S.A.; Aspnes, D.E.; Barnett, A.; Borak, T.B.; Braby, L.A.; Heimdahl, M.P.; Hyland, S.L.; Jacobson, S.H.; et al. National Academies of Sciences, Engineering, and Medicine. In Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space; The National Academies Press: Washington, DC, USA, 2018; Volume 700. [Google Scholar]
- Rodríguez, E. On the Optimal Design of Doppler Scatterometers. Remote Sens. 2018, 10, 1765. [Google Scholar] [CrossRef] [Green Version]
- Wineteer, A.; Perkovic-Martin, D.; Monje, R.; Rodríguez, E.; Gál, T.; Niamsuwan, N.; Nicaise, F.; Srinivasan, K.; Baldi, C.; Majurec, N.; et al. Measuring Winds and Currents with Ka-Band Doppler Scatterometry: An Airborne Implementation and Progress towards a Spaceborne Mission. Remote Sens. 2020, 12, 1021. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez, E.; Wineteer, A.; Perkovic-Martin, D.; Gál, T.; Stiles, B.; Niamsuwan, N.; Monje, R. Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer. Remote Sens. 2018, 10, 576. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez, E.; Wineteer, A.; Perkovic-Martin, D.; Gál, T.; Anderson, S.; Zuckerman, S.; Stear, J.; Yang, X. Ka-Band Doppler Scatterometry over a Loop Current Eddy. Remote Sens. 2020, 12, 2388. [Google Scholar] [CrossRef]
- Farrar, J.T.; D’Asaro, E.; Rodriguez, E.; Shcherbina, A.; Czech, E.; Matthias, P.; Nicholas, S.; Bingham, F.; Mahedevan, A.; Omand, M.; et al. S-MODE: The Sub-Mesoscale Ocean Dynamics Experiment. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 3533–3536. [Google Scholar] [CrossRef]
- Tanelli, S.; Durden, S.L.; Im, E. Simultaneous Measurements of Ku- and Ka-band Sea Surface Cross Sections by an Airborne Radar. IEEE Geosci. Remote Sens. Lett. 2006, 3, 359–363. [Google Scholar] [CrossRef]
- Vandemark, D.C.; Chapron, B.; Sun, J.; Crescenti, G.H.; Graber, H.C. Ocean Wave Slope Observations Using Radar Backscatter and Laser Altimeters. J. Phys. Oceanogr. 2004, 34, 2825–2842. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Ka-Band Dual Copolarized Empirical Model for the Sea Surface Radar Cross Section. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1629–1647. [Google Scholar] [CrossRef]
- Masuko, H.; Okamoto, K.; Shimada, M.; Niwa, S. Measurement of Microwave Backscattering Signatures of the Ocean Surface Using X Band and Ka Band Airborne Scatterometers. J. Geophys. Res. Ocean. 1986, 91, 13065–13083. [Google Scholar] [CrossRef]
- Walsh, E.J.; Vandemark, D.; Friehe, C.A.; Burns, S.P.; Khelif, D.; Swift, R.N.; Scott, J.F. Measuring Sea Surface Mean Square Slope with a 36-GHz Scanning Radar Altimeter. J. Geophys. Res. Ocean. 1998, 103, 12587–12601. [Google Scholar] [CrossRef] [Green Version]
- Edson, J.; Crawford, T.; Crescenti, J.; Farrar, T.; Frew, N.; Gerbi, G.; Helmis, C.; Hristov, T.; Khelif, D.; Jessup, A.; et al. The Coupled Boundary Layers and Air–Sea Transfer Experiment in Low Winds. Bull. Am. Met. Soc. 2007, 88, 341–356. [Google Scholar] [CrossRef]
- Plant, W. Microwave Sea Return at Moderate to High Incidence Angles. Waves Random Media 2003, 13, 339–354. [Google Scholar] [CrossRef] [Green Version]
- Mouche, A.; Hauser, D.; Kudryavtsev, V.N. Radar Scattering of the Ocean Surface and Sea-roughness Properties: A Combined Analysis from Dual-polarizations Airborne Radar Observations and Models in C Band. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- Hwang, P.A.; Plant, W.J. An Analysis of the Effects of Swell and Surface Roughness Spectra on Microwave Backscatter from the Ocean. J. Geophys. Res. 2010, 115, C04014. [Google Scholar] [CrossRef] [Green Version]
- Edson, J.B.; Jampana, V.; Weller, R.A.; Bigorre, S.P.; Plueddemann, A.J.; Fairall, C.W.; Miller, S.D.; Mahrt, L.; Vickers, D.; Hersbach, H. On the Exchange of Momentum over the Open Ocean. J. Phys. Oceanogr. 2013, 48, 1589–1610. [Google Scholar] [CrossRef] [Green Version]
- Stewart, R.H. Introduction to Physical Oceanography; Texas AM University: College Station, TX, USA, 2008; Available online: https://hdl.handle.net/1969.1/160216 (accessed on 2 March 2022).
- Portabella, M. Wind Field Retrieval from Satellite Radar Systems. Ph.D. Thesis, University of Barcelona, Barcelona, Spain, 2002. Available online: https://www.tdx.cat/bitstream/handle/10803/734/TOL255.PDF?sequence=1 (accessed on 19 July 2021).
- Spencer, M.W.; Wu, C.; Long, D.G. Improved Resolution Backscatter Measurements with the SeaWinds Pencil-beam Scatterometer. IEEE Trans. Geosci. Remote Sens. 2000, 38, 89–104. [Google Scholar] [CrossRef] [Green Version]
- Harris, F.J. On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Masalias, H.G. In SAR Simulations for SWOT and Dual Frequency Processing for Topographic Measurements. Master’s Thesis, University of Massachusetts Amherst, Amherst, MA, USA, 2019. [Google Scholar] [CrossRef]
- Carswell, J.R.; Donnelly, W.J.; McIntosh, R.E.; Donelan, M.A.; Vandemark, D.C. Analysis of C and Ku Band Ocean Backscatter Measurements under Low-wind Conditions. J. Geophys. Res. 1999, 104, 20687–20701. [Google Scholar] [CrossRef] [Green Version]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Chapron, B.; Grodsky, S.A. Modulation of Ka-band Doppler Radar Signals Backscattered from Sea Surface. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2931–2948. [Google Scholar] [CrossRef] [Green Version]
- Mastenbroek, K. Wind-Wave Interaction. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 12 December 1996. [Google Scholar]
- Yan, Q.; Zhang, J.; Fan, C.; Meng, J. Analysis of Ku- and Ka-Band Sea Surface Backscattering Characteristics at Low-Incidence Angles Based on the GPM Dual-Frequency Precipitation Radar Measurements. Remote Sens. 2019, 11, 754. [Google Scholar] [CrossRef] [Green Version]
- Grodsky, S.A.; Kudryavtsev, V.N.; Bentamy, A.; Carton, J.A.; Chapron, B. Does Direct Impact of SST on Short Wind Waves Matter for Scatterometry? Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- O’Neill, L.W.; Chelton, D.B.; Esbensen, S.K. Observations of SST-Induced Perturbations of the Wind Stress Field over the Southern Ocean on Seasonal Timescales. J. Clim. 2003, 16, 2340–2354. [Google Scholar] [CrossRef] [Green Version]
- Chelton, D.B.; Schlax, M.G.; Freilich, M.H.; Milliff, R.F. Satellite Measurements Reveal Persistent Small-scale Features in Ocean Winds. Science 2004, 303, 978–983. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Ka-Band Radar Cross-Section of Breaking Wind Waves. Remote Sens. 2021, 13, 1929. [Google Scholar] [CrossRef]
- Jessup, A.T.; Melville, W.K.; Keller, W.C. Breaking Waves Affecting Microwave Backscatter 1. Detection and Verification. J. Geophys. Ocean. 1991, 96, 20547–20559. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Malinovsky, V.V. Radar Backscattering from Breaking Wind Waves: Field Observation and Modelling. Int. J. Remote Sens. 2012, 33, 2462–2481. [Google Scholar] [CrossRef]











| Name | Value |
|---|---|
| Bandwidth | 100 MHz |
| Pulse Repetition Frequency | 1 kHz |
| Sample number per pulse | 391 |
| Transmit power | 9 dBm |
| Antenna peak gain | 23.58 dB |
| Boresight angle | 60° |
| H-Plane antenna aperture width | 68.88 mm |
| E-Plane antenna aperture width | 52.37 mm |
| 3 dB Azimuth Beamwidth | 10° |
| 3 dB Elevation Beamwidth | 10° |
| Platform Altitude | 13.1 m |
| Range Resolution | 1.5 m |
| Elevation Resolution | 1.6–4.4 m |
| 40° | −0.55 | +2.93 | +3.01 | +3.08 | +3.05 | +4.25 | +0.71 | +0.69 |
| 45° | −0.37 | +1.80 | +3.00 | +3.11 | +3.02 | +3.60 | +0.76 | +0.75 |
| 50° | +0.69 | +1.63 | +2.37 | +2.55 | +2.47 | +3.02 | +0.85 | +0.84 |
| 55° | +0.03 | +0.24 | +2.71 | +2.99 | +2.71 | +3.00 | +0.83 | +0.81 |
| 60° | −0.16 | +0.14 | +2.03 | +2.45 | +2.04 | +2.45 | +0.88 | +0.86 |
| 65° | +0.34 | +1.81 | +2.59 | +3.01 | +2.61 | +3.52 | +0.83 | +0.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polverari, F.; Wineteer, A.; Rodríguez, E.; Perkovic-Martin, D.; Siqueira, P.; Farrar, J.T.; Adam, M.; Closa Tarrés, M.; Edson, J.B. A Ka-Band Wind Geophysical Model Function Using Doppler Scatterometer Measurements from the Air-Sea Interaction Tower Experiment. Remote Sens. 2022, 14, 2067. https://doi.org/10.3390/rs14092067
Polverari F, Wineteer A, Rodríguez E, Perkovic-Martin D, Siqueira P, Farrar JT, Adam M, Closa Tarrés M, Edson JB. A Ka-Band Wind Geophysical Model Function Using Doppler Scatterometer Measurements from the Air-Sea Interaction Tower Experiment. Remote Sensing. 2022; 14(9):2067. https://doi.org/10.3390/rs14092067
Chicago/Turabian StylePolverari, Federica, Alexander Wineteer, Ernesto Rodríguez, Dragana Perkovic-Martin, Paul Siqueira, J. Thomas Farrar, Max Adam, Marc Closa Tarrés, and James B. Edson. 2022. "A Ka-Band Wind Geophysical Model Function Using Doppler Scatterometer Measurements from the Air-Sea Interaction Tower Experiment" Remote Sensing 14, no. 9: 2067. https://doi.org/10.3390/rs14092067
APA StylePolverari, F., Wineteer, A., Rodríguez, E., Perkovic-Martin, D., Siqueira, P., Farrar, J. T., Adam, M., Closa Tarrés, M., & Edson, J. B. (2022). A Ka-Band Wind Geophysical Model Function Using Doppler Scatterometer Measurements from the Air-Sea Interaction Tower Experiment. Remote Sensing, 14(9), 2067. https://doi.org/10.3390/rs14092067