Figure 1.
YOLOv5s 6.0 algorithm framework.
Figure 1.
YOLOv5s 6.0 algorithm framework.
Figure 2.
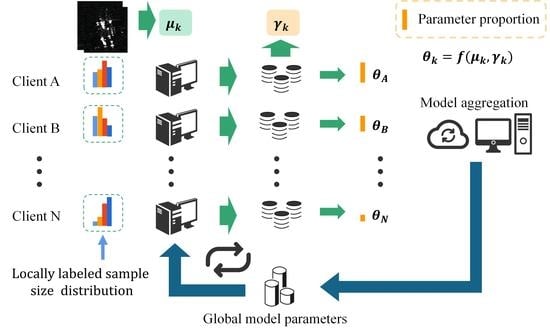
Federated learning framework.
Figure 2.
Federated learning framework.
Figure 3.
Label samples for all datasets.
Figure 3.
Label samples for all datasets.
Figure 4.
Loss functions of clients A, B, C, and D on the multiclass aircraft detection dataset using three training strategies: centralized, federally averaged, and federally distributed mean difference.
Figure 4.
Loss functions of clients A, B, C, and D on the multiclass aircraft detection dataset using three training strategies: centralized, federally averaged, and federally distributed mean difference.
Figure 5.
Test results of clients A, B, C, and D on a multiclass aircraft detection dataset using three training strategies: centralized, federated average, and federated distributed mean difference, with evaluation metrics of mAP0.5–0.95, all data taken from corresponding communication rounds (number of iterations). The Pre prefix represents the unaggregated local model, and the Post prefix represents the aggregated global model. The four left panels (a,c,e,g) show the test results of each model on the local test set, and the four right panels (b,d,f,h) show the test results of each model on the total test set.
Figure 5.
Test results of clients A, B, C, and D on a multiclass aircraft detection dataset using three training strategies: centralized, federated average, and federated distributed mean difference, with evaluation metrics of mAP0.5–0.95, all data taken from corresponding communication rounds (number of iterations). The Pre prefix represents the unaggregated local model, and the Post prefix represents the aggregated global model. The four left panels (a,c,e,g) show the test results of each model on the local test set, and the four right panels (b,d,f,h) show the test results of each model on the total test set.
Figure 6.
Test results of four clients, A, B, C, and D, on a multi-category aircraft detection dataset using three training strategies, centralized, federated average, and federated distributed mean difference, with evaluation metrics of mAP0.5–0.95. Data are from the centralized training model and the aggregated post model on the total test set.
Figure 6.
Test results of four clients, A, B, C, and D, on a multi-category aircraft detection dataset using three training strategies, centralized, federated average, and federated distributed mean difference, with evaluation metrics of mAP0.5–0.95. Data are from the centralized training model and the aggregated post model on the total test set.
Figure 7.
Performance of the global model (300 epochs) aggregated by FedDAD on the test image of dataset #1. The top is the label sample, and the bottom is the detection effect.
Figure 7.
Performance of the global model (300 epochs) aggregated by FedDAD on the test image of dataset #1. The top is the label sample, and the bottom is the detection effect.
Figure 8.
Test results of clients A, B, C, and D on a single-category aircraft detection dataset using three training strategies: centralized, federated average, and federated distributed mean difference, with evaluation metrics of mAP0.5–0.95, all data taken from corresponding communication rounds (number of iterations). The Pre prefix represents the unaggregated local model, and the Post prefix represents the aggregated global model. The four left panels (a,c,e,g) show the test results of each model on the local test set, and the four right panels (b,d,f,h) show the test results of each model on the total test set.
Figure 8.
Test results of clients A, B, C, and D on a single-category aircraft detection dataset using three training strategies: centralized, federated average, and federated distributed mean difference, with evaluation metrics of mAP0.5–0.95, all data taken from corresponding communication rounds (number of iterations). The Pre prefix represents the unaggregated local model, and the Post prefix represents the aggregated global model. The four left panels (a,c,e,g) show the test results of each model on the local test set, and the four right panels (b,d,f,h) show the test results of each model on the total test set.
Figure 9.
Test results of four clients, A, B, C, and D, on a single-category aircraft detection dataset using three training strategies, centralized, federated average, and federated distributed mean difference, with evaluation metrics of mAP0.5–0.95. Data are from the centralized training model and the post-aggregation model on the total test set.
Figure 9.
Test results of four clients, A, B, C, and D, on a single-category aircraft detection dataset using three training strategies, centralized, federated average, and federated distributed mean difference, with evaluation metrics of mAP0.5–0.95. Data are from the centralized training model and the post-aggregation model on the total test set.
Figure 10.
Experimental results of the MSAR-1.0 dataset. (a): loss of the total training set, Client A centralized training, and federated cooperative training model; (b): Results of centralized training for all clients and test results of Client A’s federated cooperative training model on a local test set, evaluated as mAP0.5(%); (c): Test results of Client A’s centralized training and federated cooperative training model on the total test set, evaluated as mAP0.5(%).
Figure 10.
Experimental results of the MSAR-1.0 dataset. (a): loss of the total training set, Client A centralized training, and federated cooperative training model; (b): Results of centralized training for all clients and test results of Client A’s federated cooperative training model on a local test set, evaluated as mAP0.5(%); (c): Test results of Client A’s centralized training and federated cooperative training model on the total test set, evaluated as mAP0.5(%).
Table 1.
Distribution average deviation factors for datasets 1 and 2 at each communication round (30 iterations for one communication round).
Table 1.
Distribution average deviation factors for datasets 1 and 2 at each communication round (30 iterations for one communication round).
| Datasets | Client\Epochs | 30 | 90 | 150 | 210 | 270 | 300 |
|---|
| Datasets one | A | 0.250360 | 0.243829 | 0.243862 | 0.245097 | 0.245503 | 0.245669 |
| B | 0.263772 | 0.274525 | 0.270521 | 0.269338 | 0.269429 | 0.268085 |
| C | 0.234626 | 0.232845 | 0.235685 | 0.235364 | 0.234702 | 0.237778 |
| D | 0.251242 | 0.247549 | 0.249931 | 0.250200 | 0.250366 | 0.248468 |
| Datasets two | A | 0.294122 | 0.296408 | 0.297204 | 0.297452 | 0.296886 | 0.296913 |
| B | 0.301700 | 0.301686 | 0.301179 | 0.301516 | 0.301283 | 0.301459 |
| C | 0.173574 | 0.172263 | 0.172206 | 0.171568 | 0.172187 | 0.171807 |
| D | 0.230604 | 0.229642 | 0.229411 | 0.229464 | 0.229644 | 0.229821 |
| MSAR-1.0 | A | 0.326456 | 0.304121 | 0.308971 | 0.316663 | 0.318955 | 0.316743 |
| B | 0.226202 | 0.22743 | 0.235625 | 0.246915 | 0.238561 | 0.239982 |
| C | 0.23388 | 0.216403 | 0.216133 | 0.217198 | 0.221301 | 0.219898 |
| D | 0.213462 | 0.252046 | 0.239271 | 0.219223 | 0.221183 | 0.223377 |
Table 2.
Distribution of Dataset 1 and Dataset 2 after dividing into four client datasets A, B, C, and D.
Table 2.
Distribution of Dataset 1 and Dataset 2 after dividing into four client datasets A, B, C, and D.
| Datasets Name | Client | Train | Test | Boeing 787 | A220 | Boeing 737–800 | Other | A320/321 | ARJ21 | A330 | Aircraft |
|---|
| Datasets one | A | 1328 | 332 | 535 | 813 | 450 | 1590 | 522 | 278 | 60 | / |
| B | 1328 | 332 | 582 | 837 | 418 | 1647 | 428 | 407 | 32 | / |
| C | 1328 | 332 | 472 | 871 | 409 | 1525 | 394 | 274 | 69 | / |
| D | 1328 | 332 | 516 | 774 | 470 | 1440 | 572 | 319 | 88 | / |
| Datasets two | A | 854 | 220 | / | / | / | / | / | / | / | 4484 |
| B | 854 | 220 | / | / | / | / | / | / | / | 4406 |
| C | 854 | 220 | / | / | / | / | / | / | / | 1168 |
| D | 854 | 220 | / | / | / | / | / | / | / | 2578 |
Table 3.
Distribution of MSAR-1.0 after dividing into four client datasets A, B, C, and D.
Table 3.
Distribution of MSAR-1.0 after dividing into four client datasets A, B, C, and D.
| Datasets Name | Client | Train | Test | Ship | Oil Tank | Bridge | Aircraft |
|---|
| MSAR-1.0 | A | 6354 | 1588 | 9498 | 10,971 | 542 | 2243 |
| B | 6354 | 1588 | 10,651 | 7660 | 323 | 1471 |
| C | 6354 | 1588 | 11,253 | 3683 | 949 | 1379 |
| D | 6354 | 1588 | 11,347 | 875 | 799 | 1275 |
Table 4.
The precision of clients A, B, C, and D using three training strategies, centralized, federated average, and federated distributed mean difference, on the multiclass aircraft detection dataset corresponding to communication rounds (number of iterations).
Table 4.
The precision of clients A, B, C, and D using three training strategies, centralized, federated average, and federated distributed mean difference, on the multiclass aircraft detection dataset corresponding to communication rounds (number of iterations).
| P | Client | Epochs | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
| A | Local | 93.1 | 91.5 | 92.8 | 92.8 | 92.1 | 91.5 | 89.8 | 91.8 | 91.3 | 91.0 |
| FedAvg | 93.1 | 92.9 | 92.5 | 92.0 | 92.3 | 92.9 | 93.2 | 92.5 | 91.4 | 93.6 |
| FedDAD | 93.1 | 94.2 | 93.6 | 92.0 | 92.8 | 90.8 | 92.1 | 91.8 | 94.2 | 94.1 |
| B | Local | 95.0 | 96.2 | 96.1 | 96.8 | 97.7 | 97.4 | 96.9 | 97.2 | 97.3 | 97.7 |
| FedAvg | 95.0 | 95.9 | 97.2 | 98.1 | 97.8 | 97.8 | 97.6 | 97.9 | 98.3 | 97.9 |
| FedDAD | 95.0 | 95.6 | 97.8 | 97.8 | 98.0 | 97.9 | 97.9 | 98.0 | 98.1 | 98.4 |
| C | Local | 91.0 | 93.8 | 95.8 | 94.4 | 96.6 | 96.8 | 95.3 | 95.7 | 95.9 | 95.3 |
| FedAvg | 91.0 | 95.3 | 95.0 | 92.9 | 96.7 | 96.1 | 96.2 | 94.2 | 96.3 | 96.2 |
| FedDAD | 91.0 | 96.1 | 96.4 | 93.8 | 96.2 | 96.8 | 95.5 | 96.4 | 96.6 | 96.7 |
| D | Local | 79.1 | 91.6 | 93.8 | 90.9 | 92.3 | 92.7 | 91.3 | 92.1 | 92.0 | 91.7 |
| FedAvg | 79.1 | 91.7 | 93.3 | 92.2 | 93.8 | 94.1 | 93.8 | 93.9 | 94.0 | 94.6 |
| FedDAD | 79.1 | 91.5 | 92.6 | 94.2 | 93.2 | 94.2 | 94.1 | 94.3 | 94.5 | 94.7 |
Table 5.
Recall clients A, B, C, and D using three training strategies, centralized, federated average, and federated distributed mean difference, on the multiclass aircraft detection dataset corresponding to communication rounds (number of iterations).
Table 5.
Recall clients A, B, C, and D using three training strategies, centralized, federated average, and federated distributed mean difference, on the multiclass aircraft detection dataset corresponding to communication rounds (number of iterations).
| R | Client | Epochs | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
| A | Local | 76.5 | 89.7 | 93.1 | 92.7 | 94.2 | 95.5 | 95.6 | 94.9 | 94.4 | 94.3 |
| FedAvg | 76.5 | 92.6 | 94.3 | 95.1 | 93.9 | 95.3 | 93.9 | 93.8 | 95.5 | 95.2 |
| FedDAD | 76.5 | 91.8 | 93.8 | 95.5 | 94.6 | 95.6 | 94.9 | 94.8 | 94.9 | 95.1 |
| B | Local | 78.6 | 92.1 | 95.3 | 93.6 | 95.6 | 95.6 | 95.3 | 95.8 | 95.9 | 95.8 |
| FedAvg | 78.6 | 95.2 | 96.5 | 97.2 | 98.1 | 98.4 | 98.3 | 98.6 | 98.8 | 98.7 |
| FedDAD | 78.6 | 95.9 | 96.2 | 96.4 | 97.2 | 98.3 | 98.2 | 98.3 | 98.9 | 98.8 |
| C | Local | 85.4 | 88.7 | 90.8 | 92.8 | 90.9 | 92.1 | 93.3 | 93.1 | 93.0 | 92.8 |
| FedAvg | 85.4 | 91.9 | 93.4 | 98.5 | 96.3 | 96.9 | 97.6 | 98.8 | 98.2 | 97.3 |
| FedDAD | 85.4 | 91.0 | 93.9 | 96.0 | 95.8 | 96.1 | 97.3 | 98.3 | 98.7 | 98.6 |
| D | Local | 83.9 | 86.7 | 89.9 | 91.4 | 90.6 | 90.9 | 91.4 | 91.5 | 90.2 | 91.6 |
| FedAvg | 83.9 | 88.2 | 94.1 | 95.2 | 96.5 | 96.6 | 96.7 | 97.3 | 97.6 | 96.8 |
| FedDAD | 83.9 | 89.9 | 94.5 | 94.9 | 96.6 | 96.9 | 97.9 | 97.6 | 97.3 | 97.5 |
Table 6.
mAP0.5 of clients A, B, C, and D using three training strategies, centralized, federated average, and federated distributed mean difference, on the multiclass aircraft detection dataset corresponding to communication rounds (number of iterations).
Table 6.
mAP0.5 of clients A, B, C, and D using three training strategies, centralized, federated average, and federated distributed mean difference, on the multiclass aircraft detection dataset corresponding to communication rounds (number of iterations).
| mAP0.5 | Client | Epochs | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
| A | Local | 89.1 | 92.9 | 94.1 | 94.0 | 94.3 | 94.9 | 94.9 | 94.7 | 94.9 | 94.9 |
| FedAvg | 89.1 | 94.6 | 95.4 | 95.8 | 95.9 | 96.1 | 95.4 | 95.9 | 95.3 | 95.4 |
| FedDAD | 89.1 | 94.2 | 96.2 | 95.5 | 95.5 | 96.0 | 95.8 | 95.7 | 96.7 | 95.8 |
| B | Local | 83.7 | 95.1 | 97.6 | 97.2 | 97.8 | 97.3 | 97.7 | 97.8 | 97.7 | 97.8 |
| FedAvg | 83.7 | 97.8 | 98.3 | 99.1 | 99.1 | 99.3 | 99.2 | 99.2 | 99.3 | 99.3 |
| FedDAD | 83.7 | 97.5 | 98.7 | 98.8 | 98.9 | 99.2 | 99.2 | 99.3 | 99.4 | 99.4 |
| C | Local | 88.4 | 93.3 | 93.4 | 93.8 | 93.8 | 94.0 | 93.8 | 93.9 | 93.8 | 94.0 |
| FedAvg | 88.4 | 96.6 | 97.4 | 98.7 | 98.7 | 98.7 | 98.4 | 98.6 | 98.4 | 98.6 |
| FedDAD | 88.4 | 96.6 | 98.8 | 97.6 | 98.3 | 98.6 | 98.4 | 98.5 | 98.7 | 98.7 |
| D | Local | 87.5 | 91.3 | 94.1 | 93.3 | 94.5 | 94.0 | 93.8 | 94.2 | 94.0 | 94.1 |
| FedAvg | 87.5 | 93.5 | 95.9 | 96.5 | 96.9 | 97.4 | 97.5 | 97.5 | 97.7 | 97.7 |
| FedDAD | 87.5 | 93.5 | 95.5 | 96.9 | 97.1 | 97.4 | 97.7 | 97.6 | 97.6 | 97.9 |
Table 7.
Test results of YOLOv5s, YOLOv7, and YOLOv8s with 300 rounds of centralized training on dataset #1.
Table 7.
Test results of YOLOv5s, YOLOv7, and YOLOv8s with 300 rounds of centralized training on dataset #1.
| Model | Size (Pixels) | Epochs | mAP0.5–0.95 | Params (M) | FLOPs (B) |
|---|
| YOLOv5s | 512 | 300 | 89.85 | 7.2 | 15.8 |
| YOLOv7 | 512 | 300 | 89.64 | 37.23 | 105.2 |
| YOLOv8s | 512 | 300 | 92.57 | 11.13 | 28.5 |
Table 8.
Compensation score (CS) for all customers using FedAvg and FedDAD in federated cooperation.
Table 8.
Compensation score (CS) for all customers using FedAvg and FedDAD in federated cooperation.
| Datasets | Method | Client A | Client B | Client C | Client D |
|---|
| Datasets #1 | FedAvg | 4.69 | 10.63 | 14.27 | 13.11 |
| FedDAD(ours) | 5.96 | 12.65 | 14.67 | 15.00 |
| Datasets #2 | FedAvg | 24.87 | 17.76 | 35.07 | 33.20 |
| FedDAD(ours) | 30.65 | 23.45 | 38.88 | 39.42 |
| MSAR-1.0 | FedAvg | 3.04 | 5.11 | 7.49 | 3.44 |
| FedDAD(ours) | 3.79 | 6.08 | 8.20 | 3.61 |