Analysis of the Differences in Internal Solitary Wave Characteristics Retrieved from Synthetic Aperture Radar Images under Different Background Environments in the Northern South China Sea

Abstract

Two internal solitary waves (ISWs) with very long fronts observed by synthetic aperture radar (SAR) images in the northern South China Sea (NSCS) are comparatively analyzed based on oceanic reanalysis data and the Korteweg–de Vries (KdV) theory. The differences in the environmental parameters, wave half-width, and amplitude of the two ISW fronts in the two distinct oceanic environments are studied. In the presence of a weak westward surface current of approximately 0.05 m/s, the values of the linear wave speed increase by up to 0.056 m/s, and the retrieved ISW amplitudes decrease by up to 14 m. On the contrary, for another background oceanic environment considering a relatively strong eastward surface current of approximately 0.2 m/s, there are decreases of up to 0.17 m/s in the linear wave speed and increases of up to 32 m in the retrieved amplitudes. However, the results retrieved from both the SAR observations commonly show that the ISW amplitudes along the fronts reach their maximums at roughly 21°N and decrease toward the southern and northern sides, in spite of their distinct background environments.

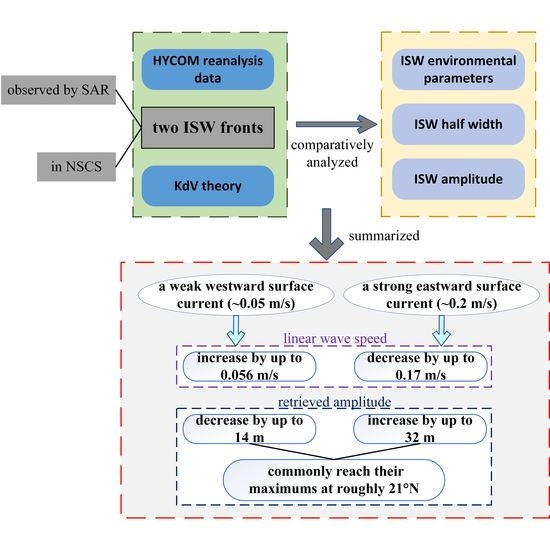
1. Introduction

Internal waves are internal fluctuations in fluids with relatively stable density stratification that have been detected at numerous locations around the world’s oceans [1,2,3,4,5]. ISWs are nonlinear gravity waves that propagate along the pycnocline in the interior of the oceans and usually result from the interaction between the barotropic tide and steep bottom bathymetry. ISWs can induce large isopycnal displacements and strong local currents, which cause intense turbulent mixing in the ocean [6]. There are many different means to study the characteristics of ISWs, e.g., laboratory experiments [7,8,9], in situ observations [10,11], theoretical and numerical analysis [12,13,14,15], and remote-sensing measurement [16,17,18]. With extensive swath coverage, remote-sensing measurement is a useful way to carry out relatively wide-range observations of ISW properties.

Particularly, the spaceborne SAR has contributed significantly to the study and understanding of oceanic ISWs [19] because it is a powerful instrument for detecting radar backscatter signals from the ocean surface under all weather and light conditions. Internal waves can induce convergence or divergence of surface flow, which modulates sea-surface roughness; thus, ISWs can be visible on SAR images as alternating bright and dark stripes [20]. Many characteristics of ISWs, such as the half-width, crest length, number of waves, propagation direction, wave speed, wave amplitude, and so on, can be retrieved from spaceborne SAR data [21,22,23,24].

Typically, there are three theoretical regimes that can describe characteristics and behaviors of internal solitons in various circumstances: shallow water [25,26]; finite depth [27,28]; and deep water [29,30]. The criteria for discriminating these three regimes depend on the ratio of the soliton horizontal scale to the water depth [31]. These theories are widely used in the parameter derivation of internal waves from remote-sensing imagery. For ISWs generated at the Columbia River plume, Pan et al. extracted the soliton dynamic parameters of the half-width, amplitude, and average energy flux per crest length along a typical section across the internal solitons using background stratification data and finite-depth theory [24]. For internal waves in the Strait of Georgia, Wang et al. found that the Benjamin–Ono equation satisfyingly describes the characteristic parameters of the studied internal waves [32]. For ISWs in the NSCS, the KdV model based on the shallow-water theory is usually applied to the study of ISWs in the NSCS and is likely to be more appropriate to estimate ISW parameters in the SCS [33,34,35,36,37,38,39].

Moreover, there may still be some differences in the results between a continuously stratified fluid model and a two-layer fluid model. For a two-layer fluid model, the accurate estimation of upper-layer thickness is crucial for the retrieval of ISW parameters because the retrieved parameters are sensitive to upper-layer thickness [40]. Although several methods have been proposed to predict upper-layer thickness, the estimations using different methods have large discrepancies [41]. Thus, the estimations of oceanic ISW parameters from SAR images by adopting a continuously stratified fluid model appear to be more realistic and suitable than those adopting a two-layer model.

It is common for ISWs to coexist with the ambient shear currents in the ocean. For instance, the kinematic and dynamic effects of ambient shear currents on the evolution of ISWs have been investigated by Liu and Benny [42] and Tung et al. [43]. Stastna and Lamb analyzed the effects of background shear on ISWs using an analytical solution and found that background shear influences the amplitude and half-width of ISWs [44]. Moreover, the presence of shear can influence environmental parameters, such as linear wave speed, nonlinear and dispersion parameters, and so on [45,46]. The above studies basically investigate the effects of ambient shear based on mooring data and theoretical model analysis. Presently, many studies on the retrieval of ISW characteristics in the NSCS from remote-sensing imagery have been carried out (e.g., Liu et al. [36]); however, to the best of our knowledge, the effects of background currents have not been carefully considered in retrieving ISW characteristics from remote-sensing images in the NSCS. Particularly, it remains uncertain if there are some discrepancies between retrieved ISW characteristics with shear and without shear.

In this study, by performing a continuously stratified shallow-water KdV-type theoretical analysis, we study the differences in ISW characteristics along the wavefronts retrieved from two SAR images under different background environments (in the presence of different ambient shear) in the NSCS. The paper is organized in the following manner. The computational methods and the data are presented in Section 2. The results are shown and discussed in Section 3. The conclusions and prospects are given in Section 4 and Section 5, respectively.

2. Data and Methods

2.1. Two SAR-Observed ISW Fronts in the Distinct Oceanic Environment

ENVISAT is an advanced polar-orbiting earth observation satellite, which provides measurements of the atmosphere, ocean, land, and ice. The advanced synthetic aperture radar (ASAR) on board this satellite operates at C-band. Due to higher sensitivity to variations in sea-surface roughness, ASAR data were acquired using VV polarization. ISWs can be seen clearly in ASAR images that have 75 m pixel spacing. Two SAR-observed ISWs (ISW1 in Figure 1a and ISW2 in Figure 1b, as adopted by Xie et al. [47] and Wang et al. [48]) near Dongsha Atoll of the NSCS at a water depth of 400–1400 m were captured on 20 July 2007 and 18 June 2008, respectively. In two images, the long ISW front propagating from generation source sites at the Luzon Strait and across the deep basin, while not reaching Dongsha Atoll, were both observed between 117 and 118°E. Furthermore, 30 transects (the red lines in Figure 1) approximately parallel to the wave-propagation direction were selected to analyze the variations in ISW characteristics along the wavefront in each SAR image. For each ISW, the intersection point of the wavefront and each transect were taken as its location. Their corresponding locations of two ISW fronts in our study region (20–22°E, 117–118°E) are presented in Figure 2. Figure 2 also reveals how the ISWs propagate regarding the background currents (see red and black arrows, respectively). Furthermore, the normalized radar cross-sections (NRCS) of ISWs along each transect was averaged in the direction perpendicular to the wave-propagation direction. Then, wave half-width can be obtained by the horizontal distribution curve of pixel backscattering intensity values (averaged NRCS).

The daily 1/12° Hybrid Coordinate Ocean Model (HYCOM) Global Ocean Forecasting System (GOFS) 3.1 reanalysis data are used to calculate the environmental parameters in the NSCS, like those in Park and Farmer [49] and Li et al. [50]. Park and Farmer validated the HYCOM data and its application in the internal wave study in the South China Sea [49]. Furthermore, Li et al. compared HYCOM data with third-party observations and other operational models, such as the Navy Coastal Ocean Model, to validate the HYCOM performance [50]. These two studies both focus on the effects of ambient currents in the South China Sea on ISW characteristics, which is consistent with our study. The subset of HYCOM data contains the variables of salinity, temperature, velocity, and sea-surface elevation. The oceanic background environments on 20 July 2007 and 18 June 2008, corresponding to the two SAR observations of ISW fronts, respectively, are apparently different (e.g., see the surface currents on these two days in Figure 2). The surface current near ISW1 front is westward and weak, while the surface current near ISW2 front is eastward and relatively strong. The bathymetry with a spatial resolution of 1 arc-minute derived from the ETOPO1 data (https://www.ngdc.noaa.gov/mgg/global/global.html, accessed on 13 February 2023) is adopted, as shown in Figure 1 and Figure 2.

2.2. Theoretical Model Analysis

Generally, the characteristic half-width of ISWs is firstly derived from SAR images. The curve-fitting method and the peak-to-peak method are the mostly used methods for the extraction of characteristic half-width of ISWs [22,23,24]. However, the ISW signals in SAR images suffer from both thermal and speckle noises. As a result, the peak-to-peak method is more applicable for the parameter estimation of ISWs than the curve-fitting method [51], which measures the locations of positive peaks and negative peaks on the curves of internal wave packet profiles. Thus, the peak-to-peak method is adopted in this study to calculate the characteristic half-width based on the KdV theory.

Considering a stratified fluid of a finite depth with rigid boundaries where buoyancy frequency is a continuous function of the depth, the eigenfunction $\varphi$ and the linear phase speed $c$ can be obtained by solving the following boundary value problem:

$$\frac{d}{dz}[{(U-c)}^2\frac{d\varphi }{dz}]+N^2\varphi =0,\varphi (0)=\varphi (-H)=0$$

(1)

where $N(z)$ is the buoyancy frequency, which is determined by the formula $N(z)={(-gd\rho /\rho dz)}^{1/2}$; $U$ is the ambient velocity along the wave direction of propagation; $N(z)$ and $U$ are both obtained from the HYCOM reanalysis data; and $\varphi (z)$ is the vertical modal function for the first mode, which is normalized by its maximum absolute value.

Small et al. developed the ISW amplitude-estimation method by applying the continuously stratified model in the KdV theory [52], which has been successfully used in the retrieval of ISW amplitude from remote-sensing images in the northern and western SCS, e.g., [22,39]. Under the Boussinesq approximation, the vertical isopycnal displacement $\eta (x,z,t)$ of ISW propagation can be described by the classical KdV equations.

$$\frac{\partial \eta }{\partial t}+c\frac{\partial \eta }{\partial x}+\alpha \eta \frac{\partial \eta }{\partial x}+\beta \frac{{\partial }^3\eta }{\partial x^3}=0$$

(2)

where $t$ is the time and $x$ is the horizontal coordinate along the propagation direction of ISWs. The parameters $\alpha$ and $\beta$ are the quadratic nonlinear coefficient and dispersion coefficient in the KdV theory, respectively.

In the continuously stratified model, the terms $\alpha$ and $\beta$ can be determined by the following formula:

$$\alpha =\frac{3{\displaystyle {\int }_{-H}^0{(c-U)}^2{(d\varphi /dz)}^{3}dz}}{2{\displaystyle {\int }_{-H}^0(c-U){(d\varphi /dz)}^{2}dz}},$$

(3)

$$\beta =\frac{{\displaystyle {\int }_{-H}^0{(c-U)}^2{\varphi }^{2}dz}}{2{\displaystyle {\int }_{-H}^0(c-U){(d\varphi /dz)}^{2}dz}}.$$

(4)

The well-known solitary wave solution to Equation (2) is

$$\eta (\xi )={\eta }_0{\mathrm{sech}}^2(\frac{\xi }{D}),\xi =x-Vt.$$

(5)

where $V=c+\frac{\alpha \eta }{3}$ is the nonlinear velocity and $D$ is the characteristic half-width of the soliton. ${\eta }_0$ refers to the ISW amplitude. The amplitude can be calculated by

$${\eta }_0=\frac{12\beta }{\alpha D^2}.$$

(6)

Accordingly, the ISW amplitude can be approximately obtained using Equation (6) if we have the background stratification profile, and the ISW characteristic half-width $D$ can be obtained through the expression $D=L/1.32$ ($L$ represents the retrieved peak-to-peak distance from the SAR images) [52]. In this study, ISW parameters under the shear and no-shear conditions are both computed to determine the response of the ISW characteristics to the ambient shear current in the NSCS. Note that in the following, $c$ $\alpha$, $\beta$, and ${\eta }_0$ represent the parameters under the no-shear condition, while $c^{\mathrm{U}}$ ${\alpha }^{\mathrm{U}}$, ${\beta }^{\mathrm{U}}$, and ${\eta }_0{}^{\mathrm{U}}$ represent the relative parameters under the shear condition.

3. Results and Discussion

3.1. Environment Parameters of ISWs

The local environmental parameters in Equation (2) have significant impacts on the behaviors of ISW evolution. Therefore, adopting the HYCOM reanalysis data near these two SAR-observed ISWs in the NSCS, these background environmental parameters given by (1), (3), and (4) are computed. Figure 3 first shows the distributions of linear wave speed $c$, parameters $\alpha$ and $\beta$ under no-shear conditions on 20 July 2007 and 18 June 2008, respectively. We can clearly see that in Figure 3a,d that the linear phase speed $c$ decreases from the southeastern to northwestern corner of the chosen domain. The general spatial variations in $c$ on these two days are similar, while $c$ at the eastern side of the domain is slightly larger for ~0.2 m/s on 18 June 2008. Additionally, the absolute values of the quadratic nonlinear parameter $\alpha$ show a similar trend in increasing from the eastern side to the western side in Figure 3b,e. The variations in the values of $\alpha$ between 117° and 118°E are distinctly larger on 20 July 2007. The distribution of the dispersion parameter $\beta$ in Figure 3c is roughly the same as that in Figure 3f. We notice that the linear wave speed $c$ and the dispersion parameter $\beta$ mainly depend on topography characteristics and have no significant temporal variation, just as depicted by Liao et al. [53].

The values of environmental parameters $c^{\mathrm{U}}$, ${\alpha }^{\mathrm{U}}$, and ${\beta }^{\mathrm{U}}$ are further computed under shear conditions, as shown in Figure 4. By comparing Figure 4 with Figure 3, we can acquire a better understanding of modulation on ISW environmental parameters by the background currents. Generally, the values of ISW environmental parameters calculated under shear conditions still decrease from the eastern to western sides of our computational region, just like that in Figure 3. However, there are some variations in the spatial distributions of the environmental parameters of ISWs in the presence of ambient shear, especially for nonlinear parameters. On the contrary, the distributions of linear wave speed and dispersion parameters change relatively less evidently. From the isolines in Figure 4a,c,d,f, the variations in linear wave speed or dispersion parameters roughly concentrate on the eastern side of the computational domain.

To better reveal the modulation of ambient shear on the environmental parameters of ISWs, the differences in these environmental parameters between shear and no-shear conditions are shown in Figure 5. Note that here, $\Delta$ refers to the operation of results with shear subtracting those without shear (e.g., $\Delta c=c^{\mathrm{U}}-c$). The variations in $c$ are roughly within $\pm 0.2$ m/s, which are close to shear on the scale. In addition, the sign of $\Delta c$ depends on the propagation direction of the ambient currents. Comparing Figure 2a (Figure 2b) with Figure 5a (Figure 5b), currents propagating westward lead to the increase in linear wave speed and vice versa. Basically, the nonlinear parameter $\alpha$ changes by within $\pm 1\times {10}^{-3}{ \mathrm{s}}^{-1}$ in the majority of the computational region, while $\Delta \alpha$ can reach a value of about $-5\times {10}^{-3}{ \mathrm{s}}^{-1}$ in the northwest corner where the bottom topography is less 300 m (Figure 5b,e). The variations in $\beta$ reaches $-5\times {10}^4{ \mathrm{m}}^3/\mathrm{s}$, as presented in Figure 5c,f. Furthermore, it is obvious that the distributions of $\Delta \beta$ shows more similarities with those of $\Delta c$ than $\Delta \alpha$, which is consistent with the relationship among distributions of $c$, $\alpha$, and $\beta$ in Figure 3 and Figure 4. This further suggests that $c$ instead of $\varphi$ is dominant in the calculation of the parameter $\beta$ (see Equation (4)).

To further understand the influence of the presence of shear on the environmental parameters in detail, the changing rates of the parameters (i.e., $\Delta c/c$, $\Delta \alpha /\left|\alpha \right|$, and $\Delta \beta /\beta$) are calculated and shown in Figure 6. Apparently, the absolute values of the changing rates of the linear wave speed $c$ and the dispersion parameter $\beta$ are within 10% of the computational domain, while those can exceed 20% for the nonlinear parameter $\alpha$. Similar to $\Delta c$, the distributions of $\Delta c/c$ are still closely related to those of ambient currents (Figure 6a,d). Larger absolute values of $\Delta \alpha /\left|\alpha \right|$ and $\Delta \beta /\beta$ are both concentrated on the northwest corner of the domain where the seas are relatively shallow, although values of $\Delta \beta$ are greater in the southeast corner.

Specifically, the environmental parameters along the ISW fronts are extracted to obtain the amplitudes of ISWs. Linear wave speed $c$ and parameters $\alpha$ and $\beta$ calculated under no-shear conditions along the ISW fronts and the bathymetry near the ISWs are presented in Figure 7. The linear wave speed $c$ keeps increasing from the northern to southern end for both ISW1 and ISW2 due to increasing water depth. The value of $c$ at the southern end is 35% greater than that at the northern end for ISW1. For ISW2, due to its greater latitudinal (bottom topography) span between the northern and southern ends, there is an increase of 65% in $c$ from the northern to southern end. The absolute values of $\alpha$ are decreasing southward, which reveals that the nonlinearity weakens southward. There are decreases of 29% and 41% in the absolute values of $\alpha$ from the northern to southern end for ISW1 and ISW2, respectively. Similar to $c$, the values of $\beta$ keep increasing southward, which represents the reinforcement in the dispersion. Due to dramatic changes in the bottom topography along the ISW fronts, the values of the dispersion parameter $\beta$ increase by a factor of 5.3 and 15.4 times from the northern to southern end for ISW1 and ISW2, respectively. Similarly, linear wave speed $c^{\mathrm{U}}$ and parameters ${\alpha }^{\mathrm{U}}$ and ${\beta }^{\mathrm{U}}$ calculated under shear conditions along the ISW fronts and the bathymetry near the ISWs are obtained, as shown in Figure 8. The general variations in each environmental parameter along the ISW fronts in the presence of ambient shear are consistent with those in Figure 7.

Figure 9 shows the differences in the environmental parameters between shear and no-shear conditions along the ISW fronts. Ambient currents lead to increases of up to 0.056 $\mathrm{m}/\mathrm{s}$ in linear wave speed $c$ along ISW1 with a surface current of averaged 0.05 m/s except the ends of the front, but the decreases of up to 0.17 $\mathrm{m}/\mathrm{s}$ in $c$ throughout the ISW2 front with a surface current average 0.2 m/s. It is noteworthy that the absolute values of the nonlinear parameter $\alpha$ decrease by up to $2.4\times {10}^{-3}{ \mathrm{s}}^{-1}$ under shear conditions along the ISW1 front, while those of $\alpha$ increase by up to $1.4\times {10}^{-3}{ \mathrm{s}}^{-1}$ with shear along the ISW2 front. Furthermore, the values of the dispersion parameter $\beta$ decrease by up to 987 ${\mathrm{m}}^3/\mathrm{s}$ (969 ${\mathrm{m}}^3/\mathrm{s}$) under shear conditions in the northern part but increase by up to 4181 ${\mathrm{m}}^3/\mathrm{s}$ (5183 ${\mathrm{m}}^3/\mathrm{s}$) in the southern part of ISW1 (ISW2).

3.2. Amplitude of ISWs

To extract amplitudes of ISWs from SAR images, the half-width of ISWs needs to be obtained first. The half-widths at 30 different locations of each ISW are calculated based on the approach adopted by Small et al. [52]. Figure 10 presents the surface current and bathymetry where SAR-observed ISWs occur, as well as the derived ISW half-widths along the ISW fronts. Obviously, the retrieved ISW widths along these two fronts are both broadened from the northern to southern end. The wave widths of ISW1 increases by 40% from the northern to southern end, while the spatial variation in wave half-width of ISW2 is appreciably larger, approximately increasing by a factor of 2.75 times from the northern to southern end. To date, several types of broadening have been reported and there are different mechanisms for the broadening of the ISW front. Zhao et al. attributed this broadening to the process of converting polarity due to bottom shoaling [37,54]. In this case, we associate the north–south broadening with the different transformation of ISWs across variable bottom topography in the NSCS deep basin, as proposed by Xie et al. [47]. Because of the spatial variations in the bottom topography, the absolute values of $\beta$ ($\alpha$) decrease (increase) greatly in the northern part, while their variations in the southern part are relatively weak (Figure 3). Therefore, according to the expression $D=\sqrt{12\beta /\alpha {\eta }_0}$, the wave width is overall narrower in the northern part than that in the southern part.

The wavefronts of ISWs in the NSCS, perpendicular to the direction of the propagation path of ISWs, can extend as long as 100–200 km [55,56]. When the internal waves radiate from the Luzon Strait into the NSCS, they are observed to be stronger in the southern part of the NSCS [57]. In the deep basin, Ramp et al. found that the ISWs are strongest along approximately 20°45′N in the latitudinal direction and become weaker toward the northern and southern sides [58]. In addition, Yang et al. found that the ISWs are asymmetric along their crests, with the average amplitude in the southern portion being 70% larger than that in the northern portion [59]. At the continental shelf break, the observed internal wave energy near Dongsha Atoll can be more than three times than that in the north [60]. When ISW passes Dongsha Atoll, the wavefront generally splits into northern and southern branches. As the two branches meet on the western side of Dongsha Atoll, complex wave-refraction patterns can be produced from ISW interactions [61,62]. Moreover, when ISWs enter the NSCS, the abundant mesoscale eddies and occasionally intruding Kuroshio can remarkably redistribute the energy along wavefronts and lead to the distortion of the crest pattern [47,63,64].

Based on Equation (6) and the distribution characteristics of ISW energy along the front, amplitudes along these two ISW fronts under no-shear and shear conditions are calculated, as shown in Figure 11 and Figure 12, respectively. Amplitudes of ISWs in different background environments (including two background environments in the absence of ambient shear and the corresponding background environments in the presence of ambient shear) commonly show a trend in increasing first and then decreasing from the northern to southern end. The maximum values of the amplitudes for these two ISWs are at roughly 21°N, regardless of whether they are calculated under shear or no-shear conditions. This latitudinal variability of the wavefront is consistent with that of the mooring observations by Ramp et al. [58], whose results indicate that the waves are strongest at the center and weaken toward the southern and northern sides. It is also noteworthy that ISW amplitudes are asymmetric along their fronts. The ISW amplitudes at the northern end are larger than those at the southern end under different background environments. We suppose that one of the reasons for this phenomenon may be associated with the stronger dispersion effect or weaker nonlinearity effect in the southern portion (see Figure 7 and Figure 8). The reliability of the results can be further verified by the similarity with the theoretical model results of Xie et al. [53]. More specifically, our results here show that the amplitude of ISW2 at the center (northern end) of the wavefront is approximately 2.4 (1.7) times greater than that of the southern end, and it is 2.6 (1.6) times greater in the theoretical model results.

Figure 13 further presents the differences in the amplitudes between shear and no-shear conditions along the ISW fronts ($\Delta {\eta }_0={\eta }_0{}^{\mathrm{U}}-{\eta }_0$). Apparently, amplitudes along ISW1 decrease under shear conditions, while there are appreciably greater increases in the amplitudes of ISW2 with shear. The sign of $\Delta {\eta }_0$ is related to the environmental parameters $\alpha$ and $\beta$ modulated by the ambient currents. The magnitude of the variations in retrieved amplitudes under shear conditions could be associated with the values of the ambient shear current. The retrieved amplitudes of ISW1 decrease by up to 14 m under weak shear with a value of approximately 0.05 m/s. In the presence of relatively strong shear with an average value of 0.2 m/s, the retrieved amplitudes of ISW2 increase by up to 32 m instead. The variation in retrieved wave amplitude implies that the neglect of ambient shear might result in a magnitude of error comparable to that resulting from the insufficiency of model resolution [65]. Therefore, the effects of the strong ambient shear currents cannot be negligible, which is especially evidenced by the increase in the average of 28% in the retrieved amplitudes of ISW2 with shear.

4. Conclusions

In this paper, the characteristics of two SAR-observed ISWs with very long fronts in the NSCS were analyzed. Based on the HYCOM reanalysis data, the environmental parameters of ISWs, including linear wave speed $c$, the quadratic nonlinear parameter $\alpha$, and the dispersion parameter $\beta$ along the ISW fronts, were calculated under shear and no-shear conditions. Then, the corresponding half-widths and the amplitudes along the ISW fronts were derived from two SAR images by adopting the KdV theory [52]. The distributions of ISW characteristics along the fronts were revealed. In addition, the environmental parameters and amplitudes of each ISW with no shear were compared with those with shear.

We found that, due to variations in the bottom topography and stratification, the absolute values of the linear wave speed $c$ (the nonlinear parameter $\alpha$) increased (decreases) by 35% (29%) and 65% (41%) from the northern to southern end for ISW1 on 20 July 2007 and ISW2 on 18 June 2008, respectively, and the dispersion parameter $\beta$ surged by a factor of 5.3 and 15.4 times southward along the fronts for ISW1 and ISW2, respectively. The half-width $D$ roughly increased along the ISW fronts with the value of $D$ at the southern end 1.4 times and 2.75 times greater than that at the northern end for ISW1 and ISW2, respectively.

In the presence of a weak westward surface current of approximately 0.05 m/s, the values of the linear wave speed increased by up to 0.056 m/s; the absolute values of the quadratic nonlinear parameter $\alpha$ decreased by up to $2.4\times {10}^{-3}{ \mathrm{s}}^{-1}$; and the values of the dispersion parameter $\beta$ decreased by up to 987 ${\mathrm{m}}^3/\mathrm{s}$ in the northern side but increased by up to 4181 ${\mathrm{m}}^3/\mathrm{s}$ in the southern side. There were decreases of up to 14 m in the retrieved amplitudes. For another background environment considering a relatively strong eastward surface of approximately 0.2 m/s, there were decreases of up to 0.17 m/s in the linear wave speed, while the quadratic nonlinear parameter $\alpha$ increased by up to $1.4\times {10}^{-3}{ \mathrm{s}}^{-1}$. Similarly, the values of the dispersion parameter $\beta$ decreased by up to 969 ${\mathrm{m}}^3/\mathrm{s}$ in the northern side but increased by up to 5183 ${\mathrm{m}}^3/\mathrm{s}$ in the southern side. There were increases of up to 32 m in the retrieved amplitudes. However, the retrieved results above commonly showed that the ISW amplitudes along the fronts were strongest at roughly 21°N and weakened toward the southern and northern sides, in spite of their distinct background environments. In addition, the ISW amplitudes were asymmetric along their fronts. The ISW amplitudes at the northern end were larger than those at the southern end under different background environments.

5. Prospects

In this study, amplitudes of ISWs under no-shear conditions are compared with those under shear conditions. The responses of the ISW environmental parameters to ambient shear and the distributions of amplitudes along the wavefronts conform well to previous studies, which could validate the performance of amplitude estimations based on the combination of SAR images and the Taylor–Goldstein equation in the long-wave approximation used in this study. However, further verification is supposed to be carried out by analyzing the deviations between the actual amplitude of an oceanic ISW and the estimations under shear or no-shear conditions based on remote-sensing imagery. A few SAR images with ISWs observed and contemporaneous in situ observations need to be acquired to carry out thorough evaluations of the method we used here, for which we hope that more insights can be provided in our prospective work.