Hyperspectral Image Classification via Spatial Shuffle-Based Convolutional Neural Network

Abstract

The unique spatial–spectral integration characteristics of hyperspectral imagery (HSI) make it widely applicable in many fields. The spatial–spectral feature fusion-based HSI classification has always been a research hotspot. Typically, classification methods based on spatial–spectral features will select larger neighborhood windows to extract more spatial features for classification. However, this approach can also lead to the problem of non-independent training and testing sets to a certain extent. This paper proposes a spatial shuffle strategy that selects a smaller neighborhood window and randomly shuffles the pixels within the window. This strategy simulates the potential patterns of the pixel distribution in the real world as much as possible. Then, the samples of a three-dimensional HSI cube is transformed into two-dimensional images. Training with a simple CNN model that is not optimized for architecture can still achieve very high classification accuracy, indicating that the proposed method of this paper has considerable performance-improvement potential. The experimental results also indicate that the smaller neighborhood windows can achieve the same, or even better, classification performance compared to larger neighborhood windows.

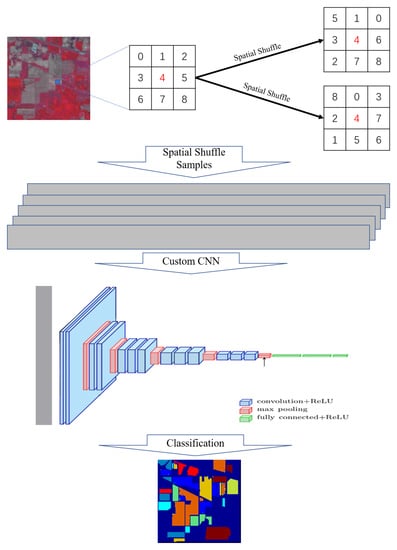
1. Introduction

The emergence and rapid development of hyperspectral remote sensing technology enables one to analyze and understand geological formations and has also prompted the development of aerospace detection technology. Hyperspectral imagery (HSI) has important applications in disaster assessment [1], biochemistry detection [2], vegetation analysis [3], environmental monitoring [4], atmospheric characterization [5], and geological mapping [6], as well as many military applications [7,8].

HSI classification generally refers to the pixel-level classification of HSI data, in which the spectral information of each pixel is an important basis. The data processing of HSI data can be simply divided into two steps: spectral feature extraction and spatial feature extraction. The spectral feature extraction of images has been widely applied and expanded in many fields from the beginning, and as an important research component, the spatial information features have also gradually received more attention and emphasis.

The structure-filtering-based HSI classification method is one of the earliest and most extensively studied methods [9], which directly acquires the spatial features of the image through spatial structure filtering. Considering the high-dimensional characteristics of HSI, the sparse representation model has also been introduced [10]. However, the sparse representation model has a high requirement for the completeness of the dictionary and is therefore not suitable for small-sample scenarios. A segmentation-based HSI classification method has been proposed to combine spatial and spectral information through segmentation [11], and probability-based methods are also employed to obtain the best category for a specific pixel using statistical methods [12]. In addition to using a single classifier to implement HSI classification, the use of classifier ensembles (multiple classifiers) can improve classification accuracy [13]. Random forest (RF) is one of the most famous models among ensemble methods and has been widely used in HSI data because it does not assume any potential probability distribution of the input data [14]. The rotation forest is proposed based on the concept of RF and achieves better classification results than the original random forest [15].

The prosperous development of the deep-learning (DL) field has attracted worldwide attention in recent years, and DL algorithms have been applied by scholars to supervised HSI classification. In terms of extracting spectral features, one-dimensional convolutional neural networks (1D CNNs) were first used for the classification of HSI [16]. Two-dimensional CNNs (2D CNNs) [17] and three-dimensional CNNs (3D CNNs) [18], which integrate spatial and spectral features, have also filled the gap of using the spatial–spectral fusion to complete HSI classification. In addition to CNNs, recurrent neural networks (RNNs) [19], graph convolutional networks (GCNs) [20], autoencoders (AEs) [21], generative adversarial networks (GANs) [22], and capsule networks (CapsNet) [23], have been used for feature extraction and classification, providing new approaches to solve the problem of HSI classification. The cascaded RNN model models spectral sequences by considering the relationships between adjacent bands, achieving high classification accuracy [24]. Building upon a comparison between CNN and GCN for hyperspectral image classification, a method called mini-batch GCN (miniGCNs) has achieved state-of-the-art classification performance [25]. From a sequence perspective, a new backbone network called SpectralFormer is proposed based on transformer architecture, significantly improving the ability to represent spectral sequence information, particularly in capturing subtle spectral differences along the spectral direction [26]. In contrast to supervised learning, semi-supervised learning and unsupervised learning do not solely rely on label information to achieve feature learning. They use information from a large amount of unlabeled data to guide model construction [27,28,29,30].

In addition to conventional semi-supervised learning, scholars have proposed the concept of few-shot learning and applied it to the field of high-spectral image classification. Zhang et al. first proposed the global prototype network to achieve few-shot learning in high-spectral imaging [31], while Gao et al. proposed a deep relational network for few-shot learning in high-spectral imaging [32]. Li et al. focused on the transfer of inter-domain information and proposed a deep cross-domain few-shot learning method [33]. These few-shot learning methods mainly study the cross-domain transfer of information, attempting to learn knowledge from a small amount of source domain samples that can be transferred to the target domain using known category information to help identify unseen categories or classes with extremely limited sample sizes. This research direction has profound practical significance, but it is still in its infancy and further exploration is needed.

Among many algorithms in few-shot learning, spectral–spatial fusion is a commonly used technique. For a pixel sample, pixels within an N × N neighborhood around the pixel are selected as a sample, the spatial and spectral features of the sample are extracted and fused, and then input into a pre-designed classification algorithm. Therefore, choosing a suitable neighborhood range, N, has a significant impact on the final classification accuracy. Paoletti et al. [34] used a 19 × 19 patch input for 2D CNN and 3D CNN, Ghamisi et al. [35] used a 27 × 27 patch for HSI classification, and the transfer learning model by Yosinski et al. employed a 32 × 32 patch [36], all of which achieved high classification performance. Moreover, larger patch sizes perform significantly better than smaller ones. Although larger patch sizes can provide more spatial features, neighborhood pixel features besides the center pixel in the patch are also trained in advance during the training process of the patch, which may result in the testing samples being trained in advance, causing the testing set and training set to be non-independent. Although smaller patch sizes may also have this pre-training issue, the degree is much smaller, making it more difficult to achieve higher classification accuracy. Therefore, developing methods for small patch sizes is more theoretically rigorous.

Due to the small sample size, there is a risk of overfitting when employing few-shot learning methods that use DL models. Therefore, effectively augmenting samples is an important issue. A deep CNN-based pixel-pair feature model (PPF) is proposed using pixel pairs composed of central pixels and neighboring pixels to build a CNN model [37] and achieves high-spectral image-classification accuracy using a majority vote strategy. The method achieved good results on small 5 × 5 patches. Inspired by this approach, a spatial shuffle scheme is proposed for small patches based on the spatial structure of neighboring pixels. Using the basic CNN architecture with this foundation can achieve a relatively high classification accuracy.

The remainder of this paper is structured as follows. The spatial shuffle scheme is described in Section 2, while the basic CNN architecture is introduced in Section 3. Comparative experiments are presented in Section 4. We provide further conclusions, including a brief summary of our work, in the last section, i.e., Section 5.

2. Proposed Method

2.1. Spatial Shuffle

Due to the sensitivity of sensor photodetectors, HSI often exhibits phenomena of the “same object different spectrum” and “different objects same spectrum”, whereby each pixel may contain multiple land cover types, resulting in a scarcity of pure pixels. According to the first law of geography, the closer the distance between objects in space is, the greater their similarity is. Therefore, in a neighborhood, the distribution of surrounding pixels can be used to infer the attributes of the central pixel. For example, when all surrounding pixels belong to a certain land cover category, the probability that the central pixel also belongs to that category is higher. Based on this principle, this paper proposes the spatial shuffle strategy, which performs a random shuffle operation on the other neighboring pixels, except for the central pixel. Each operation forms a new spatial distribution, which may represent a potential land cover distribution pattern in the real world. By simulating as many potential distribution patterns as possible, the spatial combination rules between the central and neighboring pixels can be learned, thereby improving the deep model’s ability to describe and recognize spatial relationships in the neighborhood.

Specifically, for a neighborhood size of N × N, there are N × N − 1 pixels, excluding the central pixel. While keeping the position of the central pixel unchanged, a random shuffle is performed on the other N × N − 1 pixels, resulting in a new sequence as shown in Figure 1 below.

According to the rules of permutation and combination, it can be determined that when N = 3, there are a total of 8! = 40,320 potential patterns; meanwhile, when N = 5, there are a total of 24! = 6.2 × 10²³ potential patterns. Given M samples, theoretically, M × (N × N − 1)! samples can be generated, greatly expanding the number of samples. Although there is still a significant similarity between the samples, as a potential distribution pattern describing the real world, it can provide DL models with more learning capabilities.

However, it is impossible to generate M × (N × N − 1)! new samples in the actual application process, which will result in significant memory and graphics memory consumption. Therefore, this paper adopts a compromise-based solution, setting the total sample number for each category as K, assuming the category has M samples. K/M spatial shuffle operations are performed for each sample to ensure that the total number of samples for all categories is the same. This paper sets K = 100,000, and different K values can be chosen according to the actual situation.

2.2. Basic CNN

To test the effect of a spatial shuffle on classification performance, this paper outlines a basic CNN architecture of a convolution + BN + ReLU + Maxpooling design, without any structural optimization. The datasets used are Indian Pines (IP), Salinas Valley (SV), and University of Pavia (UP), which are widely used and publicly available, with 200, 204, and 103 effective bands, respectively. A sample with an N × N neighborhood and B bands is flattened into an image with B width and N × N after each spatial shuffle, thus transforming the three-dimensional cube of N × N × B into a two-dimensional image. For example, for the Indian Pines dataset, if N = 5, each sample is transformed into a 25 × 200 image for subsequent CNN network training.

As the band number in the three datasets is inconsistent, to maintain the original data dimensions, we designed the following three deep CNN networks in

Table 1. The basic CNN networks used for 5 × 5 patches.

	IP	SV	UP
Seq_1	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32
	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32
	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32
	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32
	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32
	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32
	Maxpool_2 × 1	Maxpool_2 × 1	Maxpool_2 × 1
	Conv-BN-ReLU, (3 × 1), 32	Conv-BN-ReLU, (3 × 1), 32	Conv-BN-ReLU, (3 × 1), 32
	Conv-BN-ReLU, (3 × 1), 32	Conv-BN-ReLU, (3 × 1), 32	Conv-BN-ReLU, (3 × 1), 32
	Maxpool_2 × 1	Maxpool_2 × 1	Maxpool_2 × 1
	Conv-BN-ReLU, (3 × 1), 32	Conv-BN-ReLU, (3 × 1), 32	Conv-BN-ReLU, (3 × 1), 32
	Maxpool_1 × 2	Maxpool_1 × 2	Maxpool_1 × 2
Seq_2	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32
	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32
	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32	Conv-BN-ReLU, (1 × 3), 32
	Maxpool_1 × 2	Maxpool_1 × 2	Maxpool_1 × 2
Seq_3	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64
	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64
	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64	Maxpool_1 × 2
	Maxpool_1 × 2	Maxpool_1 × 2
Seq_4	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64
	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64
	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64
	Maxpool_1 × 2	Maxpool_1 × 2
Seq_5	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64
	Conv-BN-ReLU, (1 × 3), 64	Conv-BN-ReLU, (1 × 3), 64
		Conv-BN-ReLU, (1 × 3), 64
Seq_6	FC-64	FC-64	FC-64
	FC-classnum	FC-classnum	FC-classnum

for use with 5 × 5 patches:

The term Conv-BN-ReLU refers to each convolution layer that was followed by a batch normalization (BN) layer and rectified linear unit (ReLU) layer. Furthermore, (1 × 3) refers to the use of a convolution kernel size of 1 × 3, while 32 and 64 indicate the use of 32 and 64 convolution kernels, respectively. Similar to the VGG network, the network designed in this paper used a large number of small convolution kernels of 1 × 3 or 3 × 1 to achieve an equivalent field of view to that of a larger convolution kernel, while also reducing the number of parameters.

Taking the network for IP dataset as an example, with an input size of 25 × 200, we can see from the network structure that in Seq_1, four 1 × 3 convolution kernels were first used to extract features within the width dimension, reducing the dimensions to 25 × 192. Then, two 3 × 1 convolution kernels were used to convolve within the height dimension, reducing the dimensions to 21 × 192. After passing through the first 2 × 1 Maxpooling, the dimensions became 10 × 192. After two 3 × 1 convolution layers and 2 × 1 Maxpooling, the dimensions became 3 × 192. Finally, after passing through a 3 × 1 convolution layer and a 1 × 2 Maxpooling, the dimensions became 1 × 96. After Seq_2 to Seq_5, the dimensions became 1 × 45, 1 × 19, 1 × 6, and 1 × 1, respectively. After passing through the two fully connected layers in Seq_6 and Softmax, we received classnum classification results. The network structures of the other two datasets were essentially the same as that of Indian Pines, with some layers having different kernel numbers and convolutional layers due to differences in the number of bands.

From the above structure, we can see that the role of Seq_1 is to extract features from the height dimension, which can be understood as extracting spatial features of HSI in the neighborhood. The subsequent layers extracted spectral features of the sample. By the combination of spatial and spectral features, the category classification for each sample was formed.

3. Experiments and Results

3.1. Dataset

We used three publicly available HSI datasets, i.e., IP, SV, and UP, to demonstrate the effectiveness and generalization of the proposed method and compared its performance with commonly used methods. For each dataset, the values were first normalized to the range of 0–1. Then, for each class, 200 pixels and their surrounding 5 × 5 neighborhoods were randomly selected as the training samples, and the remaining pixels were used as the testing samples. These settings are the same as those in [37].

The IP dataset was obtained in northwestern Indiana, using the airborne visible infrared imaging spectrometer (AVIRIS) sensor. The original dataset had 224 bands, and after removing bands 104–108, 150–163, and 220 that contained voids or water vapor absorption, 220 bands were left. The spectral range was 0.4 to 2.5 μm. The spatial resolution was 20 m, and the image size was 145 × 145. The annotated ground truth contained 16 land cover categories, such as crops, forests, etc., with a total of 10,249 pixels, accounting for about half of the total pixels. However, the pixel number in seven categories was too small [38]; thus, this paper selected nine other categories for experimentation. The selected classes and their sample sizes are shown in

Table 2. The samples chosen from IP dataset.

No.	Class Name	Training Num	Testing Num	All Num
0	Background	-	-	10,776
1	Alfalfa	-	-	46
2	Corn-notill	200	1228	1428
3	Corn-min	200	630	830
4	Corn	-	-	237
5	Grass/Pasture	200	283	483
6	Grass/Trees	200	530	730
7	Grass/pasture-mowed	-	-	28
8	Hay-windrowed	200	278	478
9	Oats	-	-	20
10	Soybeans-notill	200	772	972
11	Soybeans-min	200	2255	2455
12	Soybean-clean	200	393	593
13	Wheat	-	-	205
14	Woods	200	1065	1265
15	Bldg-Grass-Tree-Drives	-	-	386
16	Stone-steel towers	-	-	93
	Total	1800	7434	21,025

below.

The SV dataset was also collected using the AVIRIS sensor and located in the Salinas Valley, California. After removing 20 bands containing water vapor and noise, 204 bands were left with a data size of 512 × 217. The spatial resolution was 3.7 m. There were 16 land cover categories in the ground truth map, and specific land cover types and pixel numbers were in

Table 3. The samples chosen from SV dataset.

No.	Class Name	Training Num	Testing Num	All Num
0	Background	-	-	56,975
1	Brocoli-gree-weeds-1	200	1809	2009
2	Brocoli-gree-weeds-2	200	3526	3726
3	Fallow	200	1776	1976
4	Fallow-rough-plow	200	1194	1394
5	Fallow-smooth	200	2478	2678
6	Stubble	200	3759	3959
7	Celery	200	3379	3579
8	Grapes-untrained	200	11,071	11,271
9	Soil-vinyard-develop	200	6003	6203
10	Corn-senesced-green-weeds	200	3078	3278
11	Lettuce-romaine-4wk	200	868	1068
12	Lettuce-romaine-5wk	200	1727	1927
13	Lettuce-romaine-6wk	200	716	916
14	Lettuce-romaine-7wk	200	870	1070
15	Vinyard-untrained	200	7068	7268
16	Vinyard-vertical-trellis	200	1607	1807
	Total	3200	50,929	111,104

as follows:

The UP dataset was obtained using the reflective optics system imaging spectrometer (ROSIS) sensor, covering part of the University of Pavia campus in the north of Italy. The noise and other unwanted bands were removed, and only 103 bands remained. The image size was 610 × 340 and the spatial resolution was 1.3 m. The spectral range was between 0.43 and 0.86 μm. About 20% of the pixels were labeled with ground truth, including various urban structures, soils, natural targets, and shadows. The specific number of pixels was in

Table 4. The samples chosen from UP dataset.

No.	Class Name	Training Num	Testing Num	All Num
0	Background	-	-	164,624
1	Asphalt	200	6431	6631
2	Meadows	200	18,449	18,649
3	Gravel	200	1899	2099
4	Trees	200	2864	3064
5	Painted metal sheets	200	1145	1345
6	Bare Soil	200	4829	5029
7	Bitumen	200	1130	1330
8	Self-Blocking Bricks	200	3482	3682
9	Shadows	200	747	947
	Total	1800	40,976	207,400

as follows:

3.2. Parameter Settings

The software environment used for the experiments in this paper was Pytorch 1.0 and Python 3.6. The GPU hardware was NVIDIA TITAN XP, with a single card having 12 GB of memory. As the focus of this paper was not to design an exceptionally superior DL model, the model parameters were set based on experience using the Adam optimizer, and the learning rate was 0.0001. The batch size for the UP dataset was set to 1024, while for the SV and IP datasets, it was set to 512. The cross-entropy loss was used as the loss function.

For evaluating the effectiveness and accuracy of the proposed approach, various methods were used, including multinomial logistic regression (MLR) [39], support vector machines (SVM) [38], extreme learning machines (ELM) [40], random forests (RF) [41], CNN2D [34], and PPF [37]. The experiments were based on the same training and testing sets. MLR, SVM, and RF were implemented using the scikit-learn machine-learning library, while ELM was implemented using the scikit-elm library. Both CNN2D and PPF used a 5 × 5 neighborhood. For CNN2D, two 3 × 3 convolutional layers + BN layer + ReLU layer were used, followed by a fully connected layer for pixel classification, identical to [34]. The classification accuracy of various methods was evaluated using the overall accuracy (OA), average accuracy (AA), and Kappa coefficient. The OA was obtained by calculating the number of correctly classified pixels divided by the total number of pixels to be classified, while AA was the arithmetic mean of classification accuracies for each class. The Kappa coefficient reflects the consistency between the classified image and the ground truth image, with a range of −1 to 1, typically greater than 0.

3.3. Results on the IP Dataset

Figure 2 below shows the classification performance of various methods on the IP dataset, from which we can see that all methods perform well within Hay-windrowed and Grass/Trees classes. With the exception of MLR, other methods also had good results within the Woods class. However, traditional machine-learning methods (MLR, SVM, RF, ELM) performed poorly for other classes, with a lot of misclassifications. CNN2D, PPF, and the proposed method based on DL performed well for all classes, with the proposed method showing fewer misclassifications, indicating good classification ability.

The

Table 5. The classification performance on the IP dataset.

	MLR	SVM	RF	ELM	CNN2D	PPF	Proposed
Corn-notill	42.59	63.84	61.97	78.34	88.03	97.31	98.53
Corn-min	37.44	66.20	68.63	81.98	96.19	95.49	99.65
Grass/Pasture	70.52	95.52	92.16	95.15	98.13	99.25	99.25
Grass/Trees	95.28	100.00	98.11	100.00	100.00	99.81	100.00
Hay-windrowed	100.00	100.00	99.64	100.00	100.00	100.00	100.00
Soybeans-notill	62.58	72.10	84.22	85.01	95.31	95.70	97.52
Soybeans-min	62.00	63.76	64.35	61.68	76.23	86.94	96.25
Soybean-clean	36.64	84.48	79.39	93.64	99.75	100.00	100.00
Woods	87.79	98.12	96.62	98.40	100.00	99.81	99.72
OA	63.42	76.12	76.68	81.04	89.93	94.73	98.26
AA	66.09	82.67	82.79	88.24	94.85	97.15	98.99
Kappa	0.5647	0.7184	0.7259	0.7776	0.8810	0.9371	0.9792

below shows the classification accuracy of each method on each class, as well as the OA, AA, and Kappa. From the table, it can be seen that the accuracy of all methods is close to 100% for the Grass/Trees and Hay-windrowed classes. MLR performed poorly for other classes, resulting in the lowest overall accuracy and Kappa coefficient. The performances of SVM and RF were similar, while ELM and CNN2D performed better. The proposed method performed well for all classes, with the overall accuracy being 3.5% higher than the second-ranked PPF and about 35% higher than the worst MLR. All these results show that the proposed method demonstrated higher classification performance.

3.4. Results on the SV Dataset

Figure 3 below shows the classification thematic maps of each method on the SV dataset. It is obvious that the performance of each method is relatively poor on the Grapes-untrained and Vinyard vertical trellis classes, with the visual performance of the MLR method being the worst. However, the proposed method can provide a relatively clean thematic map. The CNN2D method had a larger misclassification rate on the Brocoli-gree-weeds-1 class, while other methods performed better for this class.

The

Table 6. The classification performance on the SV dataset.

	MLR	SVM	RF	ELM	CNN2D	PPF	Proposed
Brocoli-gree-weeds-1	97.82	98.85	99.43	99.83	62.41	100	100
Brocoli-gree-weeds-2	97.82	99.89	99.74	99.83	100	100	100
Fallow	92.06	99.38	99.04	97.75	99.94	99.77	99.94
Fallow-rough-plow	99.08	99.5	99.41	99.16	100	99.66	99.92
Fallow-smooth	97.7	98.14	97.54	98.71	97.58	98.35	99.56
Stubble	99.46	99.92	99.81	99.87	100	100	99.97
Celery	99.4	99.91	99.29	99.76	99.76	99.97	99.97
Grapes-untrained	70.44	85.03	61.66	83.83	89.59	83.92	95.71
Soil-vinyard-develop	96.21	99.48	98.83	99.92	99.92	99.9	99.98
Corn-senesced-green-weeds	85.44	94.37	88.28	94.37	94.64	98.51	98.84
Lettuce-romaine-4wk	92.44	97.52	93.15	94.92	99.41	100	99.65
Lettuce-romaine-5wk	99.64	99.82	97.63	99.23	99.94	100	100
Lettuce-romaine-6wk	98.86	99.71	98.15	99	100	99.57	100
Lettuce-romaine-7wk	91.19	98.24	94.83	94.36	99.65	99.29	99.18
Vinyard-untrained	62.78	69.36	69.64	69.41	73.93	85.82	94.33
Vinyard-vertical-trellis	91.08	98.76	98.27	98.69	99.72	99.45	99.93
OA	85.84	91.84	86	91.47	92.36	94.31	98.16
AA	91.96	96.12	93.42	95.54	94.78	97.76	99.19
Kappa	0.8417	0.9086	0.8441	0.9044	0.9142	0.9364	0.9794

below shows the quantitative objective evaluation metrics of various methods for all classes. It is clear that the proposed method performed the best within almost all classes, with the overall accuracy (OA) being about 4% higher than the PPF method and approximately 12% higher than the worst-performing MLR method. The CNN2D method performed the worst on the Brocoli-gree-weeds-1 class, consistent with the visual judgment. The MLR method had the lowest accuracy for the Vinyard-untrained and Grapes-untrained classes, which directly lowered the overall accuracy. The proposed method had the highest OA, AA, and Kappa values, indicating that it had the highest classification ability and performance.

3.5. Results on the UP Dataset

The thematic map of the UP dataset is shown in Figure 4 below. The classification ability of various methods can be clearly seen from the misclassification of the three categories with the most pixels: Asphalt, Bare Soil, and Meadows. MLR had the most misclassifications, while the proposed method had the lowest level of misclassification, followed by PPF and CNN2D. The performance of the other machine-learning methods did not differ significantly.

The objective evaluation criteria in the

Table 7. The classification performance on the UP dataset.

	MLR	SVM	RF	ELM	CNN2D	PPF	Proposed
Asphalt	73.55	88.94	81.32	62.08	96.01	98.2	99.64
Meadows	75.77	93.72	78.4	91.2	90.46	97.78	99.53
Gravel	76.95	85.23	76.89	81.66	95.73	91.67	97.78
Trees	93.06	96.02	94.96	95.14	97.57	96.55	97.75
Painted metal sheets	99.21	99.65	99.56	99.48	100	99.91	100
Bare Soil	73.49	90.43	82.61	83.35	98.92	97.54	99.88
Bitumen	89.12	91.59	90.35	91.95	98.76	94.42	98.32
Self-Blocking Bricks	74.73	83.46	78.89	68.12	90.09	92.19	98.71
Shadows	99.87	100	100	99.87	100	99.87	100
OA	77.83	91.68	81.86	83.91	93.76	96.97	99.3
AA	83.97	92.12	87	85.87	96.39	96.46	99.07
Kappa	0.7152	0.8898	0.7662	0.7888	0.9181	0.9595	0.9906

below show that the OA value of the MLR method was the lowest, and SVM performed the best among the four traditional machine-learning algorithms but was slightly inferior to the three DL-based methods. The proposed method can provide the highest classification accuracy for all categories, resulting in an overall accuracy of 99.3%, indicating that the proposed method showed the best classification ability for this dataset.

4. Discussion

4.1. Classification Ability with Less Samples

To compare the accuracy performance of various methods with fewer training samples, according to [34,37], this paper set the number of each type of training sample to 50, 100, 150, and 200, respectively, and used the same method to calculate the classification performance of various methods. The results are listed in Figure 5 below. Overall, with the increase in training samples, the classification performance of various methods on various datasets showed an upward trend, which is consistent with the general perception. SVM performed with a relative stability for several datasets and had a relatively excellent performance within traditional machine-learning algorithms. Due to the random generation of the weight matrix and the hidden layer threshold from input neurons to hidden neurons, ELM can cause the output matrix to be ill-conditioned when there are individual samples with large deviations among the training samples. The resulting network structure is unstable and has poor robustness, which reduces the classification performance of the network; hence, its performance was not very stable on these three datasets. The DL-based methods performed significantly better than traditional machine-learning-based methods for various training sample sizes across all three datasets. Moreover, the proposed method consistently showed the best classification ability.

4.2. Effects of Neighborhood Sizes

The role of the neighboring pixels is to provide spatial feature description ability for the center pixel. The larger the neighborhood is, the more spatial features can be extracted. Therefore, existing HSI classification methods based on spatial–spectral fusion mostly used larger neighborhoods. The earlier experiments in this paper used a neighborhood size of 5 × 5. To evaluate the impact of neighborhood size on classification accuracy, similar to [37], we compared three neighborhood sizes: 3 × 3, 5 × 5, and 7 × 7. As can be seen from Figure 6 below, with the neighborhood size increased, the classification performance improved significantly. However, the improvement intensity of 7 × 7 compared with 5 × 5 was not as large as that of 5 × 5 compared with 3 × 3, indicating that the improvement resulting from increasing the neighborhood size is limited. It should be pointed out that the CNN structure designed for the three datasets needed to be modified for the different neighborhood size. The larger the neighborhood is, the more layers the modified network will have, and the computation will be greater. Therefore, after balancing multiple factors, we chose a neighborhood size of 5 × 5 for the experiments and discussion.

4.3. Effects of Spatial Shuffle

After the operation of a spatial shuffle, a 5 × 5 neighborhood can produce up to 6.2 × 10²³ potential patterns, but it is impossible to produce so many samples within its practical application. Therefore, we randomly generated 100,000 samples for each class to increase the sample size. Intuitively, the more samples there are, the better the description of the real world is. However, this also increases the amount of computation. In order to evaluate the impact of the sample size on classification accuracy, we set four sample size levels: 50,000, 100,000, 200,000, and 300,000. Meanwhile, we also compared the performance without spatial shuffle, which means there were only 200 original training samples for each category. Using the same network structure, the final classification performance was evaluated, and the results are shown in Figure 7 below.

It can be seen that, without spatial shuffle, the classification performance on each dataset was significantly lower compared to the case with spatial shuffle. In particular, for the IP dataset, the classification accuracy was only around 0.65, while with spatial shuffle using 50,000 samples per class, the accuracy could reach around 0.97. The other two datasets also had an accuracy of around 0.9 without spatial shuffle, which was noticeably lower than with spatial shuffle using 50,000 samples per class. Without spatial shuffle, considering the experimental setup, there were only 200 samples per class for the IP and UP datasets, resulting in a total of 9 × 200 = 1800 samples. For the SV dataset, there was a total of 16 × 200 = 3200 samples. Training a CNN model on such small datasets easily leads to overfitting, which is the main reason for the low classification accuracy. However, by using spatial shuffle, the training samples can be expanded to 9 × 50,000 = 450,000 samples, or even more. This helps to mitigate the impact of overfitting and the significant improvement in classification accuracy further confirms this. With the increase in sample size, the classification performance for all three datasets improved. However, the degree of improvement generally tended to become saturated, not following a linear trend with the increase in sample size. Therefore, from a multi-factor balance perspective, our choice of 100,000 samples per class was reasonable. To further improve classification accuracy, future study will focus on optimizing the network structure.

5. Conclusions

Existing spatial–spectral fusion-based HSI classification methods mostly adopt larger neighborhoods to extract more spatial features to assist in the fine classification of each pixel. However, large neighborhoods may cause the problem of non-independence between the training set and testing set to some extent. Therefore, minimizing the neighborhood size may alleviate the above problem. This paper proposes a strategy called spatial shuffle, which randomly shuffles the positions of the pixels in the small neighborhood to simulate potential patterns that may exist in the real world. Through spatial shuffle, it is possible to quickly generate more simulated samples given a certain initial sample set. Experimental results have shown that this strategy effectively addresses the data requirement and overfitting issues in deep learning, leading to improved classification accuracy. The number of initial samples also has a decisive impact on the final classification accuracy. Although spatial shuffle allows for the generation of almost infinite samples to mimic the distribution patterns in the real world, the diversity of the initial samples may still be limited, which can restrict the simulated distribution patterns. However, even with this limitation, applying the spatial shuffle strategy and using the basic CNN model can achieve a consistently higher classification accuracy than traditional machine-learning methods and previously optimized CNN models. In addition, designing a deep-learning CNN model is not the focus of this paper; a simple CNN architecture based on convolution, batch normalization, and ReLU was constructed without any optimization measures, and the spatial shuffle samples were used for training. The experimental results indicate that the proposed method can effectively extract spatial and spectral features to improve the HSI classification performance. Different neighborhood window sizes can extract varying levels of spatial information, which also significantly affects the classification accuracy. By designing different network structures, it is possible to adapt to different sizes of neighborhood window sizes. Combined with the spatial shuffle strategy, it becomes possible to achieve classification accuracy comparable to previous studies using larger neighborhood window sizes even with smaller window sizes. This approach partially addresses the issue of overlapping and dependent training and testing samples during the training process. However, it should be noted that this paper only utilizes the basic, unoptimized CNN model and achieves remarkably high classification accuracy. Therefore, it is foreseeable that further improvement in classification performance can be achieved by optimizing the structure of the CNN model. Thus, future research will further explore the potential advantages of a spatial shuffle and optimize the constructed basic CNN architecture to further improve the accuracy of HSI classification.