Study on the Polarization Pattern Induced by Wavy Water Surfaces
Abstract
:1. Introduction
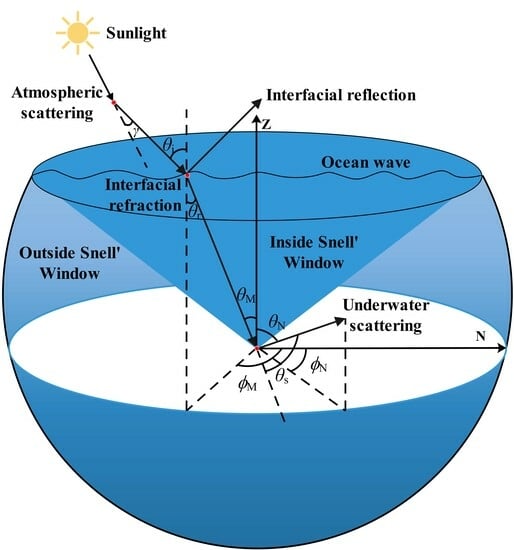
2. Methods
2.1. Atmospheric Scattering
2.2. Reflection and Refraction of Air–Water Interface
2.3. Underwater Scattering
3. Results and Discussion
3.1. Polarization Patterns Reflected by Wavy Water Surfaces
3.2. Polarization Patterns inside Snell’s Window under Wavy Water Surfaces
3.3. Polarization Patterns outside Snell’s Window under Wavy Water Surfaces
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lambrinos, D.; Möller, R.; Labhart, T.; Pfeifer, R.; Wehner, R. A mobile robot employing insect strategies for navigation. Robot. Auton. Syst. 2000, 30, 39–64. [Google Scholar] [CrossRef]
- Schwind, R. Spectral regions in which aquatic insects see reflected polarized light. J. Comp. Physiol. A 1995, 177, 439–448. [Google Scholar] [CrossRef]
- Lerner, A.; Sabbah, S.; Erlick, C.; Shashar, N. Navigation by light polarization in clear and turbid waters. Philos. Trans. R. Soc. B 2011, 366, 671–679. [Google Scholar] [CrossRef] [PubMed]
- Lynch, D.K. Snell’s window in wavy water. Appl. Opt. 2015, 54, B8–B11. [Google Scholar] [CrossRef]
- Waterman, T.H. Polarization patterns in submarine illumination. Science 1954, 120, 927–932. [Google Scholar] [CrossRef]
- Tonizzo, A.; Zhou, J.; Gilerson, A.; Twardowski, M.S.; Gray, D.J.; Arnone, R.A.; Gross, B.M.; Moshary, F.; Ahmed, S.A. Polarized light in coastal waters: Hyperspectral and multiangular analysis. Opt. Express 2009, 17, 5666–5682. [Google Scholar] [CrossRef]
- Sabbah, S.; Barta, A.; Gal, J.; Horvath, G.; Shashar, N. Experimental and theoretical study of skylight polarization transmitted through Snell’s window of a flat water surface. J. Opt. Soc. Am. A 2006, 23, 1978. [Google Scholar] [CrossRef]
- Ivanoff, A.; Waterman, T.H. Factors, mainly depth and wavelength, affecting the degree of underwater light polarization. J. Mar. Res. 1958, 16, 283–307. [Google Scholar]
- Waterman, T.H. Polarization of scattered sunlight in deep water. Deep Sea Res. 1955, 3, 426–434. [Google Scholar]
- Shashar, N.; Sabbah, S.; Cronin, T.W. Transmission of linearly polarized light in seawater: Implications for polarization signaling. J. Exp. Biol. 2004, 207, 3619–3628. [Google Scholar] [CrossRef]
- Sabbah, S.; Lerner, A.; Erlick, C.; Shashar, N. Under water polarization vision-A physical examination. Recent Res. Dev. Exp. Theor. Biol. 2005, 1, 123–176. [Google Scholar]
- Goddard, S.M.; Forward, R.B. The role of the underwater polarized light pattern, in sun compass navigation of the grass shrimp, Palaemonetes vulgaris. J. Comp. Physiol. A 1991, 169, 479–491. [Google Scholar] [CrossRef]
- Shashar, N.; Hagan, R.; Boal, J.G.; Hanlon, R.T. Cuttlefish use polarization sensitivity in predation on silvery fish. Vis. Res. 2000, 40, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Waterman, T.H. Reviving a neglected celestial underwater polarization compass for aquatic animals. Biol. Rev. 2006, 81, 111–115. [Google Scholar] [CrossRef] [PubMed]
- Cartron, L.; Josef, N.; Lerner, A.; McCusker, S.D.; Darmaillacq, A.S.; Dickel, L.; Shashar, N. Polarization vision can improve object detection in turbid waters by cuttlefish. J. Exp. Mar. Biol. Ecol. 2013, 447, 80–85. [Google Scholar] [CrossRef]
- Cheng, H.; Chu, J.; Zhang, R.; Tian, L.; Gui, X. Underwater polarization patterns considering single Rayleigh scattering of water molecules. Int. J. Remote Sens. 2020, 41, 4947–4962. [Google Scholar] [CrossRef]
- Cheng, H.; Chu, J.; Zhang, R.; Tian, L.; Gui, X. Turbid underwater polarization patterns considering multiple Mie scattering of suspended particles. Photogramm. Eng. Remote Sens. 2020, 86, 737–743. [Google Scholar] [CrossRef]
- Cheng, H.; Chu, J.; Zhang, R.; Zhang, P. Simulation and measurement of the effect of various factors on underwater polarization patterns. Optik 2021, 237, 166637. [Google Scholar] [CrossRef]
- Cheng, H.; Chu, J.; Zhang, R.; Gui, X.; Tian, L. Real-time position and attitude estimation for homing and docking of an autonomous underwater vehicle based on bionic polarized optical guidance. J. Ocean Univ. China 2020, 19, 1042–1050. [Google Scholar] [CrossRef]
- Cheng, H.; Chu, J.; Chen, Y.; Liu, J.; Gong, W. Polarization-based underwater image enhancement using the neural network of Mueller matrix images. J. Mod. Opt. 2022, 69, 264–271. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, D.; Zhu, J.; Yu, H.; Chu, J. Underwater target detection utilizing polarization image fusion algorithm based on unsupervised learning and attention mechanism. Sensors 2023, 23, 5594. [Google Scholar] [CrossRef] [PubMed]
- Harrison, A.W.; Coombes, C.A. Angular distribution of clear sky short wavelength radiance. Sol. Energy 1988, 40, 57–63. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurement of the roughness of the sea surface from photographs of the sun’s glitter. J. Opt. Soc. Am. 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Hess, M.; Koepke, P.; Schult, I. Optical properties of aerosols and clouds: The software package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Risović, D. Two-component model of sea particle size distribution. Deep Sea Res. Part I 1993, 40, 1459–1473. [Google Scholar] [CrossRef]
- Risović, D.; Martinis, M. A comparative analysis of sea-particle-size distribution models. Fizika B 1995, 4, 111–120. [Google Scholar]
- You, Y.; Tonizzo, A.; Gilerson, A.A.; Cummings, M.E.; Brady, P.; Sullivan, J.M.; Twardowski, M.S.; Dierssen, H.M.; Ahmed, S.A.; Kattawar, G.W. Measurements and simulations of polarization states of underwater light in clear oceanic waters. Appl. Opt. 2011, 50, 4873–4893. [Google Scholar] [CrossRef]
- Gal, J.; Horvath, G.; Meyer-Rochow, V.B. Measurement of the reflection–polarization pattern of the flat water surface under a clear sky at sunset. Remote Sens. Environ. 2001, 76, 103–111. [Google Scholar] [CrossRef]
- Bhandari, P.; Voss, K.J.; Logan, L.; Twardowski, M. The variation of the polarized downwelling radiance distribution with depth in the coastal and clear ocean. J. Geophys. Res.-Ocean. 2011, 116, C00H10. [Google Scholar] [CrossRef]
- Cheng, H.; Yu, S.; Yu, H.; Zhu, J.; Chu, J. Bioinspired underwater navigation using polarization patterns within Snell’s window. China Ocean Eng. 2023, 37, 628–636. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, Q.; Zeng, X.; Yuan, H.; Zhang, L. The polarized light field enables underwater unmanned vehicle bionic autonomous navigation and automatic control. J. Mar. Sci. Eng. 2023, 11, 1603. [Google Scholar] [CrossRef]
- Powell, S.B.; Garnett, R.; Marshall, J.; Rizk, C.; Gruev, V. Bioinspired polarization vision enables underwater geolocalization. Sci. Adv. 2018, 4, eaao6841. [Google Scholar] [CrossRef] [PubMed]














Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Zhang, Q.; Wan, Z.; Zhang, Z.; Qin, J. Study on the Polarization Pattern Induced by Wavy Water Surfaces. Remote Sens. 2023, 15, 4565. https://doi.org/10.3390/rs15184565
Cheng H, Zhang Q, Wan Z, Zhang Z, Qin J. Study on the Polarization Pattern Induced by Wavy Water Surfaces. Remote Sensing. 2023; 15(18):4565. https://doi.org/10.3390/rs15184565
Chicago/Turabian StyleCheng, Haoyuan, Qianli Zhang, Zhenhua Wan, Zhongyuan Zhang, and Jin Qin. 2023. "Study on the Polarization Pattern Induced by Wavy Water Surfaces" Remote Sensing 15, no. 18: 4565. https://doi.org/10.3390/rs15184565
APA StyleCheng, H., Zhang, Q., Wan, Z., Zhang, Z., & Qin, J. (2023). Study on the Polarization Pattern Induced by Wavy Water Surfaces. Remote Sensing, 15(18), 4565. https://doi.org/10.3390/rs15184565